7.1.1 两条直线相交 课件(共18张PPT) 2024-2025学年人教版数学七年级下册
文档属性
| 名称 | 7.1.1 两条直线相交 课件(共18张PPT) 2024-2025学年人教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 535.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-15 13:17:02 | ||
图片预览





文档简介
(共18张PPT)
7.1相交线
7.1.1两条直线相交
理解并掌握邻补角与对顶角的概念.
在具体情景中了解邻补角与对顶角,能找出图形中一个角的邻补角与对顶角,理解对顶角相等,并能运用它解决一些简单问题.
通过动手操作、推断交流等方式,进一步发展空间观念,培养识图能力、推理能力和清晰的表达能力.
1
2
3
【重点】理解并掌握邻补角与对顶角的概念.
【难点】在具体情景中了解邻补角与对顶角,并能运用它解决一 些简单问题.
A
D
C
B
A
B
D
C
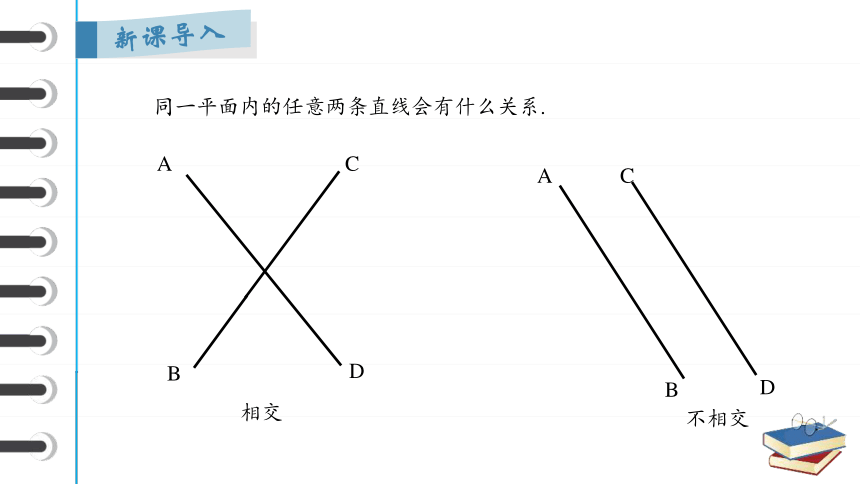
同一平面内的任意两条直线会有什么关系.
相交
不相交
如下图所示生活中的剪刀可以看作两条相交的直线.
A
D
C
B
O
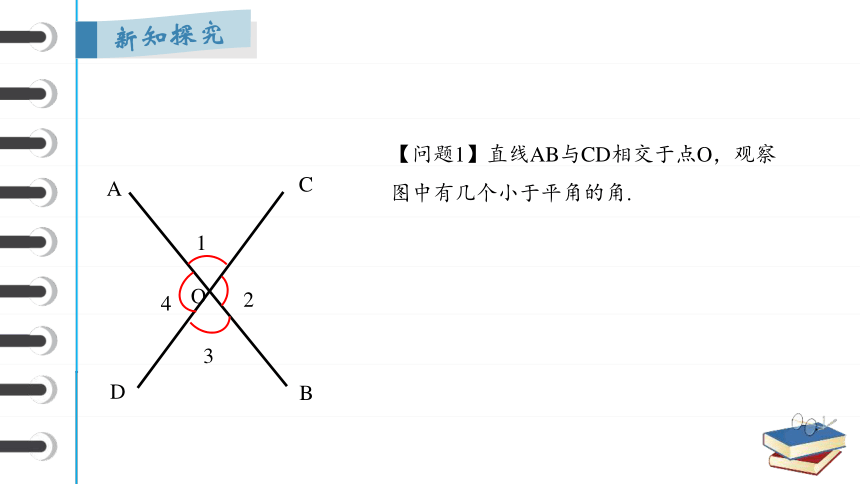
【问题1】直线AB与CD相交于点O,观察图中有几个小于平角的角.
A
D
C
B
O
1
2
3
4
A
D
C
B
O
1
2
3
4
【问题2】两个角之间形成了怎样的位置关系?
邻补角:如果两个角有一条________,它们的另一边互为___________,那么这两个角互为_______.图中∠1的邻补角是__________.
公共边
反向延长线
邻补角
∠2和∠4
A
D
C
B
O
1
2
3
4
对顶角:如果两个角有一个________,并且一个角的两边是另一个角的两边的_________,那么这两个角互为_________.图中∠1的对顶角是______.
公共顶点
反向延长线
对顶角
∠3
【问题2】两个角之间形成了怎样的位置关系?
1、下列各图中∠1和∠2是互为邻补角吗?
2、下列各图中∠1和∠2是互为对顶角吗?
基础练习
A
D
C
B
O
1
2
3
4
【问题3】分别测量各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
因为 ∠1和∠2互补、∠2和∠3互补(邻补角)
对顶角相等
所以 ∠1=∠3(同角的补角相等)
1
2
3
a
4
例1 如图,直线a、b相交,∠1=40°,求∠2, ∠3, ∠4的度数.
解:由∠1和∠2互为邻补角,得
∠2=180°- ∠1=180°-40°=140°
由对顶角相等,得
∠3= ∠1=40°, ∠4= ∠2=140°
b
1、理解邻补角与对顶角的概念:
2、对顶角的性质:
邻补角:①公共边 ②反向延长线
对顶角:①公共顶点 ②反向延长线
对顶角相等
1.如图,将一把剪刀固定在某个角度,他们想象成两条直线,就能得到一个相交线的模型,你能说出其中的邻补角与对顶角吗?,剪刀所形成的角中,如果∠1=60°,其他三个角各是多少度?如果∠1等于83°,133°,m°呢?
1
2
3
4
解:∠1和∠2、∠4互为邻补角
∠3和∠2、∠4互为邻补角
∠1和∠3互为对顶角
∠2和∠4互为对顶角
如果∠1=60°,那么∠3=60°,∠2=∠4=120°
如果∠1=83°,那么∠3=83°,∠2=∠4=97°
查漏补缺
1.(判断题)下列说法是否正确.(正确的打√,错误的打×)
①对顶角相等 ( )
②相等的两个角是对顶角 ( )
③有公共顶点并且相等的两个角是对顶角 ( )
④互为邻补角的两个角之和为180° ( )
×
√
×
√
查漏补缺
1.若∠1+∠3=70°,则∠1,∠2,∠3,∠4的度数分别为_______________________.
2.若∠2是∠1的 2倍,则∠1,∠2,∠3,∠4的度数分别为_________________________.
3 .若∠1:∠2=2:7 ,则∠1,∠2,∠3,∠4的度数分别为_______________________.
35°、145°、35°、145°
60°、120°、60°、120°
40°、140°、40°、140
2.如图直线ab相交于点O,若以下条件,各角的度数分别为多少度?
查漏补缺
3.如图,直线AB、CD,EF相交于点O,∠1=40°, ∠BOC=110°求∠2的度数.
解:因为 ∠1=40°,
∠ BOC=110°
所以 ∠ BOF=∠BOC-∠1
=110-40°
=70°
因为 ∠BOF=∠2(对顶角相等)
所以 ∠2=70° (等量代换)
提升能力
4.如图,直线AB、CD、EF相交,若∠1+∠5=180°找出图中与∠1相等的角.
解:因为 ∠1=∠3(对顶角相等),
∠5+∠8 =180°且∠1+∠5=180°
所以 ∠8=∠1
又因为 ∠8=∠6(对顶角相等)
所以 ∠6=∠1
提升能力
【解决问题】生活处处是数学
小明爸爸作为施工方要求工人们为小区修建一个六边形的花坛,要求每个花坛转角都是120°,小明爸爸要求小明检验图中花坛转角是否合格,请你替小明设计检测方法.
A
B
0
解:过点O作OB的延长线,测量∠AOB的邻补角∠AOC是否为60°即可.
你还有其他方法吗?
C
7.1相交线
7.1.1两条直线相交
理解并掌握邻补角与对顶角的概念.
在具体情景中了解邻补角与对顶角,能找出图形中一个角的邻补角与对顶角,理解对顶角相等,并能运用它解决一些简单问题.
通过动手操作、推断交流等方式,进一步发展空间观念,培养识图能力、推理能力和清晰的表达能力.
1
2
3
【重点】理解并掌握邻补角与对顶角的概念.
【难点】在具体情景中了解邻补角与对顶角,并能运用它解决一 些简单问题.
A
D
C
B
A
B
D
C
同一平面内的任意两条直线会有什么关系.
相交
不相交
如下图所示生活中的剪刀可以看作两条相交的直线.
A
D
C
B
O
【问题1】直线AB与CD相交于点O,观察图中有几个小于平角的角.
A
D
C
B
O
1
2
3
4
A
D
C
B
O
1
2
3
4
【问题2】两个角之间形成了怎样的位置关系?
邻补角:如果两个角有一条________,它们的另一边互为___________,那么这两个角互为_______.图中∠1的邻补角是__________.
公共边
反向延长线
邻补角
∠2和∠4
A
D
C
B
O
1
2
3
4
对顶角:如果两个角有一个________,并且一个角的两边是另一个角的两边的_________,那么这两个角互为_________.图中∠1的对顶角是______.
公共顶点
反向延长线
对顶角
∠3
【问题2】两个角之间形成了怎样的位置关系?
1、下列各图中∠1和∠2是互为邻补角吗?
2、下列各图中∠1和∠2是互为对顶角吗?
基础练习
A
D
C
B
O
1
2
3
4
【问题3】分别测量各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
因为 ∠1和∠2互补、∠2和∠3互补(邻补角)
对顶角相等
所以 ∠1=∠3(同角的补角相等)
1
2
3
a
4
例1 如图,直线a、b相交,∠1=40°,求∠2, ∠3, ∠4的度数.
解:由∠1和∠2互为邻补角,得
∠2=180°- ∠1=180°-40°=140°
由对顶角相等,得
∠3= ∠1=40°, ∠4= ∠2=140°
b
1、理解邻补角与对顶角的概念:
2、对顶角的性质:
邻补角:①公共边 ②反向延长线
对顶角:①公共顶点 ②反向延长线
对顶角相等
1.如图,将一把剪刀固定在某个角度,他们想象成两条直线,就能得到一个相交线的模型,你能说出其中的邻补角与对顶角吗?,剪刀所形成的角中,如果∠1=60°,其他三个角各是多少度?如果∠1等于83°,133°,m°呢?
1
2
3
4
解:∠1和∠2、∠4互为邻补角
∠3和∠2、∠4互为邻补角
∠1和∠3互为对顶角
∠2和∠4互为对顶角
如果∠1=60°,那么∠3=60°,∠2=∠4=120°
如果∠1=83°,那么∠3=83°,∠2=∠4=97°
查漏补缺
1.(判断题)下列说法是否正确.(正确的打√,错误的打×)
①对顶角相等 ( )
②相等的两个角是对顶角 ( )
③有公共顶点并且相等的两个角是对顶角 ( )
④互为邻补角的两个角之和为180° ( )
×
√
×
√
查漏补缺
1.若∠1+∠3=70°,则∠1,∠2,∠3,∠4的度数分别为_______________________.
2.若∠2是∠1的 2倍,则∠1,∠2,∠3,∠4的度数分别为_________________________.
3 .若∠1:∠2=2:7 ,则∠1,∠2,∠3,∠4的度数分别为_______________________.
35°、145°、35°、145°
60°、120°、60°、120°
40°、140°、40°、140
2.如图直线ab相交于点O,若以下条件,各角的度数分别为多少度?
查漏补缺
3.如图,直线AB、CD,EF相交于点O,∠1=40°, ∠BOC=110°求∠2的度数.
解:因为 ∠1=40°,
∠ BOC=110°
所以 ∠ BOF=∠BOC-∠1
=110-40°
=70°
因为 ∠BOF=∠2(对顶角相等)
所以 ∠2=70° (等量代换)
提升能力
4.如图,直线AB、CD、EF相交,若∠1+∠5=180°找出图中与∠1相等的角.
解:因为 ∠1=∠3(对顶角相等),
∠5+∠8 =180°且∠1+∠5=180°
所以 ∠8=∠1
又因为 ∠8=∠6(对顶角相等)
所以 ∠6=∠1
提升能力
【解决问题】生活处处是数学
小明爸爸作为施工方要求工人们为小区修建一个六边形的花坛,要求每个花坛转角都是120°,小明爸爸要求小明检验图中花坛转角是否合格,请你替小明设计检测方法.
A
B
0
解:过点O作OB的延长线,测量∠AOB的邻补角∠AOC是否为60°即可.
你还有其他方法吗?
C
同课章节目录
