北师大版六年级上册数学第八周思维训练课时钟问题(2)(课件)(共22张PPT)
文档属性
| 名称 | 北师大版六年级上册数学第八周思维训练课时钟问题(2)(课件)(共22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
(6°-0.5°)
转速差
= ÷
两针的夹角
从3时开始,再过多长时间,时针正好与分针重合?
追及时间 = 路程差 ÷ 速度差
重合时间
90°
÷ =
(分)
答:再过 分钟,时针正好和分针重合。
复习:
思维训练课
时钟问题(2)
小学 / 数学 / 北师大版 / 六年级上册
知识回顾:
1、时针走1大格用( )小时,也就是( )分,分针走1大格
用( )分。
2、钟面上的大格有( )个,小格有( )个。
3、钟面上每个大格对应的角度是( )度,小格是( )度。
4、时针每分钟旋转( )度,分针每分钟旋转( )度。
5、如果分针的速度用1表示,则时针的速度用( )表示。
1
60
5
12
60
30
6
0.5
6
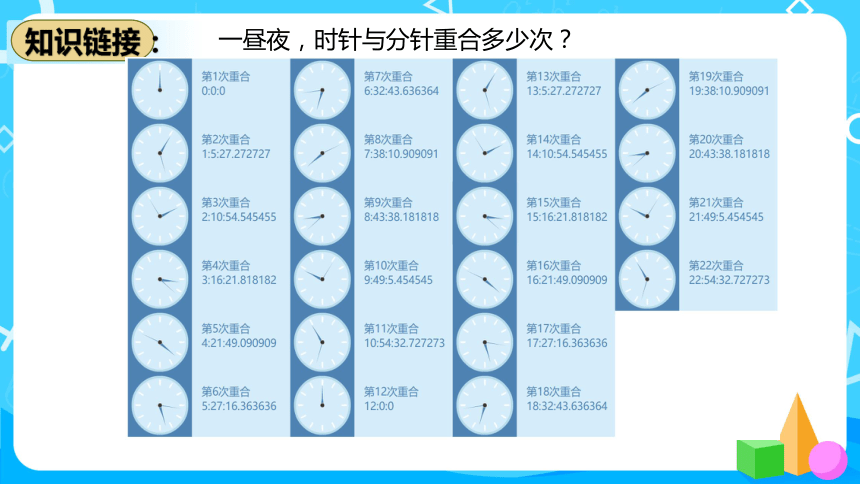
一昼夜,时针与分针重合多少次?
360÷(6-0.5)
例题1:
思路点拨:分针每小时走一圈,每分钟走360÷60=6度,时针每小时走1大格,时针每分钟走30÷60= 0.5度。设从0:00开始,下一次重合时,分针比时针多走了360度。重合时间可以用追及问题的计算方法求出,从而计算出一昼夜重合的次数。
第一次重合经过的时间:
=
=360÷5.5
解:设经过x分钟两针重合。
6x- 0.5x = 360
5.5x=360
x=
一昼夜,时针与分针重合多少次?
360÷(6-0.5)
例题1:
第一次重合经过的时间:
=
=360÷5.5
解:设经过x分钟两针重合。
6.x- 0.5x = 360
5.5x=360
x=
60÷(1-)
=60÷
=
一昼夜,时针与分针重合多少次?
例题1:
第一次重合经过的时间:
一昼夜=24时=1440分
1440÷
=
=1440×
答:一昼夜,时针与分针重合22次。
一昼夜,时针与分针重合多少次?
知识链接:
从中午12时开始,到晚上9时,分针与时针重合多少次?
360÷(6-0.5)=
答:分针与时针重合8次。
练一练:
9小时=540分
540÷=540=8.25(次)
比8次多,还不到9次。
6时多少分,分针和时针成直角?
( -90°)
180°
÷(6°-0.5°)=
例题2:
思路点拨:从6时开始,在分针追上时针之前,分针与时针可以成一次直角,在追上时针后,在7时之前,两针还可以成一次直角。
第一次成直角:
6时的时候,时针与分针相距180°,要使两针之间的夹角是90°,分针要比时针多走90°,也就是追及路程是90°
6时多少分,分针和时针成直角?
( - 15)
30
÷(1-)=
例题2:
思路点拨:从6时开始,在分针追上时针之前,分针与时针可以成一次直角,在追上时针后,在7时之前,两针还可以成一次直角。
第一次成直角:
6时的时候,时针与分针相距的时间相当于30分,要使两针垂直,分针要比时针多走15分钟的路程,也就是追及路程是30-15=15分。
6时多少分,分针和时针成直角?
( -90°)
180°
÷(6°-0.5°)=
例题2:
思路点拨:从6时开始,在分针追上时针之前,分针与时针可以成一次直角,在追上时针后,在7时之前,两针还可以成一次直角。
第一次成直角:
30
( - 15)
÷(1-)=
无论是将追及路程用角度表示,还是用时间表示,都是将这类问题转化成“追及问题”,用“路程差÷速度差=追及时间”这个数量关系式解答。
6时多少分,分针和时针成直角?
( +90°)
180°
÷(6°-0.5°)=
答:6时 分和6时 分,分针和时针是直角。
例题2:
思路点拨:从6时开始,在分针追上时针之前,分针与时针可以成一次直角,在追上时针后,在7时之前,两针还可以成一次直角。
第二次成直角:
第二次成直角要在第一次成直角的基础上,分针再比时针多走半圈(180°或30分钟)
30
( + 15)
÷(1-)=
7时以后,经过多少分的时候,时针与分针成直角?
答:7时分和7时分的时候,时针与分针成直角。
练一练:
(210-90)÷(6-0.5)
=120÷5.5
=
(35-15)÷(1-)
=20÷
=
(210+90)÷(6-0.5)
=300÷5.5
=
(35+15)÷(1-)
=50÷
=
思路点拨:第一次重合,就相当于分针比时针多走了90°;第一次成一条直线,就相当于分针要先追上时针后再比比时针多走180°。
例题3:
一个时钟现在显示的时间是3点整,请问:
(1)多少分钟后,时针与分针第一次重合?
(2)多少分钟后,时针与分针第一次张开成一条直线?
第一次重合:
90÷(6-0.5)
=90÷5.5
=
第一次成直线:
(90+180)÷(6-0.5)
=270÷5.5
=
答:分后第一次重合,分后第一次成一条直线。
一个钟显示的时间是9点整,请问:
(1)多少分钟后,时针和分针第一次重合?
(2)多少分钟后,时针和分针第一次张开成一条直线?
第一次重合:
270÷(6-0.5)
=270÷5.5
=
第一次成直线:
(270-180)÷(6-0.5)
=90÷5.5
=
答:分后第一次重合,分后第一次成一条直线。
练一练:
思路点拨:在8点到9点之间,两针由成一条直线到重合,说明分针追上时针180°的路程。用追及问题的解题思路可以解决。
例题4:
晚上8点刚过不一会小华开始做作业,一看钟,时针与分针正好成一条直线.做完作业再看钟,还不到9点,而且分针与时针恰好重合.小华做作业用了多长时间?
180÷(6-0.5)
=180÷5.5
=
≈
开始
结束
30÷(1-)
=30÷
=
≈
答:小华做作业用了32.73分钟。
晚上7点多的时候小芳开始锻炼,此时时针和分钟刚好垂直.当小芳锻炼结束的时候时针和分针刚好重合,且此时还没有到8点.请问:小芳锻炼了多久?
90÷(6-0.5)
=90÷5.5
=
≈
开始
结束
15÷(1-)
=15÷
=
≈
答:小芳锻炼用了16.36分钟。
练一练:
从5时开始,时针与分针第一次与“5”的距离相等,并分别在“5”的两旁,过了几分钟?
(30°×5)
(6°+0.5°)
÷ =
答:过了 分钟。
例题5:
思路点拨:遇到钟面上两针与某一数字等距离问题时,将钟面上的等距离问题转化为“相遇问题”。相遇时间=路程÷速度和。
相遇的路程:30°×5=150°
两针速度和:6°+0.5°=6.5°
从5时开始,时针与分针第一次与“5”的距离相等,并分别在“5”的两旁,过了几分钟?
(5×5)
(1+)
÷ =
答:过了 分钟。
例题5:
思路点拨:将钟面上的等距离问题转化为“相遇问题”。相遇时间=路程÷速度和
相遇的路程:5分×5=25分
两针速度和:1+=
从5时开始,时针与分针第一次与“5”的距离相等,并分别在“5”的两旁,过了几分钟?
(30°×5)
(6°+0.5°)
÷ =
例题5:
思路点拨:将钟面上的等距离问题转化为“相遇问题”。相遇时间=路程÷速度和
(5×5)
(1+)
÷ =
两针的相遇路程用两针之间的角度表示。
两针的相遇路程用两针之间的时间表示。
从4时开始,时针和分针第一次与“3”的距离相等,并分别在“3”的两旁,过了几分钟?
(30°×2)
(6°+0.5°)
÷ =
答:过了 分钟。
练一练:
提示:两针在数字3的两旁,时针应该超过4一点点,分针差一点到2。两针的相遇路程是两大格。
总结:
这节课有什么收获?
(6°-0.5°)
转速差
= ÷
两针的夹角
从3时开始,再过多长时间,时针正好与分针重合?
追及时间 = 路程差 ÷ 速度差
重合时间
90°
÷ =
(分)
答:再过 分钟,时针正好和分针重合。
复习:
思维训练课
时钟问题(2)
小学 / 数学 / 北师大版 / 六年级上册
知识回顾:
1、时针走1大格用( )小时,也就是( )分,分针走1大格
用( )分。
2、钟面上的大格有( )个,小格有( )个。
3、钟面上每个大格对应的角度是( )度,小格是( )度。
4、时针每分钟旋转( )度,分针每分钟旋转( )度。
5、如果分针的速度用1表示,则时针的速度用( )表示。
1
60
5
12
60
30
6
0.5
6
一昼夜,时针与分针重合多少次?
360÷(6-0.5)
例题1:
思路点拨:分针每小时走一圈,每分钟走360÷60=6度,时针每小时走1大格,时针每分钟走30÷60= 0.5度。设从0:00开始,下一次重合时,分针比时针多走了360度。重合时间可以用追及问题的计算方法求出,从而计算出一昼夜重合的次数。
第一次重合经过的时间:
=
=360÷5.5
解:设经过x分钟两针重合。
6x- 0.5x = 360
5.5x=360
x=
一昼夜,时针与分针重合多少次?
360÷(6-0.5)
例题1:
第一次重合经过的时间:
=
=360÷5.5
解:设经过x分钟两针重合。
6.x- 0.5x = 360
5.5x=360
x=
60÷(1-)
=60÷
=
一昼夜,时针与分针重合多少次?
例题1:
第一次重合经过的时间:
一昼夜=24时=1440分
1440÷
=
=1440×
答:一昼夜,时针与分针重合22次。
一昼夜,时针与分针重合多少次?
知识链接:
从中午12时开始,到晚上9时,分针与时针重合多少次?
360÷(6-0.5)=
答:分针与时针重合8次。
练一练:
9小时=540分
540÷=540=8.25(次)
比8次多,还不到9次。
6时多少分,分针和时针成直角?
( -90°)
180°
÷(6°-0.5°)=
例题2:
思路点拨:从6时开始,在分针追上时针之前,分针与时针可以成一次直角,在追上时针后,在7时之前,两针还可以成一次直角。
第一次成直角:
6时的时候,时针与分针相距180°,要使两针之间的夹角是90°,分针要比时针多走90°,也就是追及路程是90°
6时多少分,分针和时针成直角?
( - 15)
30
÷(1-)=
例题2:
思路点拨:从6时开始,在分针追上时针之前,分针与时针可以成一次直角,在追上时针后,在7时之前,两针还可以成一次直角。
第一次成直角:
6时的时候,时针与分针相距的时间相当于30分,要使两针垂直,分针要比时针多走15分钟的路程,也就是追及路程是30-15=15分。
6时多少分,分针和时针成直角?
( -90°)
180°
÷(6°-0.5°)=
例题2:
思路点拨:从6时开始,在分针追上时针之前,分针与时针可以成一次直角,在追上时针后,在7时之前,两针还可以成一次直角。
第一次成直角:
30
( - 15)
÷(1-)=
无论是将追及路程用角度表示,还是用时间表示,都是将这类问题转化成“追及问题”,用“路程差÷速度差=追及时间”这个数量关系式解答。
6时多少分,分针和时针成直角?
( +90°)
180°
÷(6°-0.5°)=
答:6时 分和6时 分,分针和时针是直角。
例题2:
思路点拨:从6时开始,在分针追上时针之前,分针与时针可以成一次直角,在追上时针后,在7时之前,两针还可以成一次直角。
第二次成直角:
第二次成直角要在第一次成直角的基础上,分针再比时针多走半圈(180°或30分钟)
30
( + 15)
÷(1-)=
7时以后,经过多少分的时候,时针与分针成直角?
答:7时分和7时分的时候,时针与分针成直角。
练一练:
(210-90)÷(6-0.5)
=120÷5.5
=
(35-15)÷(1-)
=20÷
=
(210+90)÷(6-0.5)
=300÷5.5
=
(35+15)÷(1-)
=50÷
=
思路点拨:第一次重合,就相当于分针比时针多走了90°;第一次成一条直线,就相当于分针要先追上时针后再比比时针多走180°。
例题3:
一个时钟现在显示的时间是3点整,请问:
(1)多少分钟后,时针与分针第一次重合?
(2)多少分钟后,时针与分针第一次张开成一条直线?
第一次重合:
90÷(6-0.5)
=90÷5.5
=
第一次成直线:
(90+180)÷(6-0.5)
=270÷5.5
=
答:分后第一次重合,分后第一次成一条直线。
一个钟显示的时间是9点整,请问:
(1)多少分钟后,时针和分针第一次重合?
(2)多少分钟后,时针和分针第一次张开成一条直线?
第一次重合:
270÷(6-0.5)
=270÷5.5
=
第一次成直线:
(270-180)÷(6-0.5)
=90÷5.5
=
答:分后第一次重合,分后第一次成一条直线。
练一练:
思路点拨:在8点到9点之间,两针由成一条直线到重合,说明分针追上时针180°的路程。用追及问题的解题思路可以解决。
例题4:
晚上8点刚过不一会小华开始做作业,一看钟,时针与分针正好成一条直线.做完作业再看钟,还不到9点,而且分针与时针恰好重合.小华做作业用了多长时间?
180÷(6-0.5)
=180÷5.5
=
≈
开始
结束
30÷(1-)
=30÷
=
≈
答:小华做作业用了32.73分钟。
晚上7点多的时候小芳开始锻炼,此时时针和分钟刚好垂直.当小芳锻炼结束的时候时针和分针刚好重合,且此时还没有到8点.请问:小芳锻炼了多久?
90÷(6-0.5)
=90÷5.5
=
≈
开始
结束
15÷(1-)
=15÷
=
≈
答:小芳锻炼用了16.36分钟。
练一练:
从5时开始,时针与分针第一次与“5”的距离相等,并分别在“5”的两旁,过了几分钟?
(30°×5)
(6°+0.5°)
÷ =
答:过了 分钟。
例题5:
思路点拨:遇到钟面上两针与某一数字等距离问题时,将钟面上的等距离问题转化为“相遇问题”。相遇时间=路程÷速度和。
相遇的路程:30°×5=150°
两针速度和:6°+0.5°=6.5°
从5时开始,时针与分针第一次与“5”的距离相等,并分别在“5”的两旁,过了几分钟?
(5×5)
(1+)
÷ =
答:过了 分钟。
例题5:
思路点拨:将钟面上的等距离问题转化为“相遇问题”。相遇时间=路程÷速度和
相遇的路程:5分×5=25分
两针速度和:1+=
从5时开始,时针与分针第一次与“5”的距离相等,并分别在“5”的两旁,过了几分钟?
(30°×5)
(6°+0.5°)
÷ =
例题5:
思路点拨:将钟面上的等距离问题转化为“相遇问题”。相遇时间=路程÷速度和
(5×5)
(1+)
÷ =
两针的相遇路程用两针之间的角度表示。
两针的相遇路程用两针之间的时间表示。
从4时开始,时针和分针第一次与“3”的距离相等,并分别在“3”的两旁,过了几分钟?
(30°×2)
(6°+0.5°)
÷ =
答:过了 分钟。
练一练:
提示:两针在数字3的两旁,时针应该超过4一点点,分针差一点到2。两针的相遇路程是两大格。
总结:
这节课有什么收获?
同课章节目录
