西师大版五年级上册数学《不规则图形的面积》课件(共14张ppt)
文档属性
| 名称 | 西师大版五年级上册数学《不规则图形的面积》课件(共14张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-13 21:56:34 | ||
图片预览


文档简介
(共14张PPT)
不规则图形的面积
西师版小学数学五年级上册第五单元
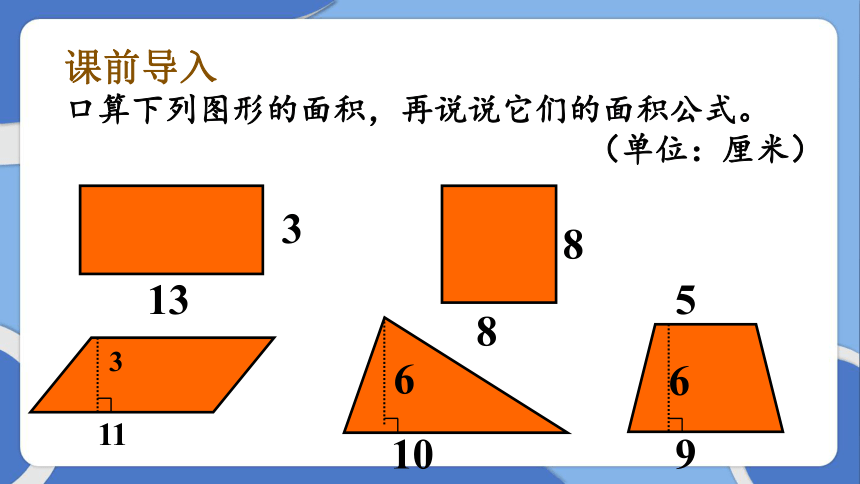
课前导入
口算下列图形的面积,再说说它们的面积公式。
(单位:厘米)
3
13
8
8
11
3
10
6
6
5
9
探究新知
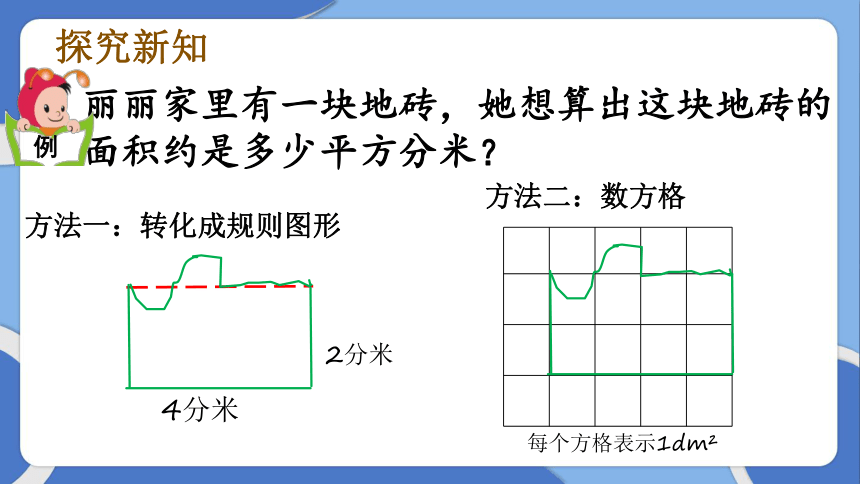
丽丽家里有一块地砖,她想算出这块地砖的
面积约是多少平方分米?
例
4分米
2分米
每个方格表示1dm
方法一:转化成规则图形
方法二:数方格
探究新知
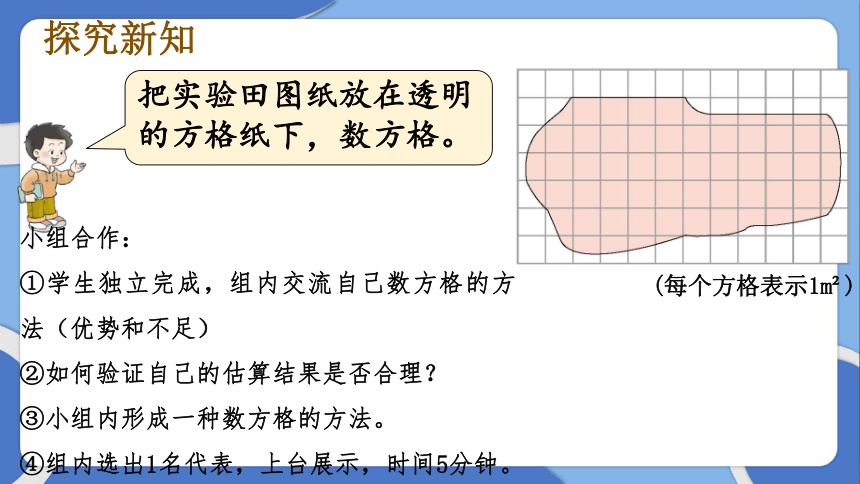
实验田大约有多大?
例
(每个方格表示1m )
把实验田图纸放在透明的方格纸下,数方格。
探究新知
小组合作:
①学生独立完成,组内交流自己数方格的方法(优势和不足)
②如何验证自己的估算结果是否合理?
③小组内形成一种数方格的方法。
④组内选出1名代表,上台展示,时间5分钟。
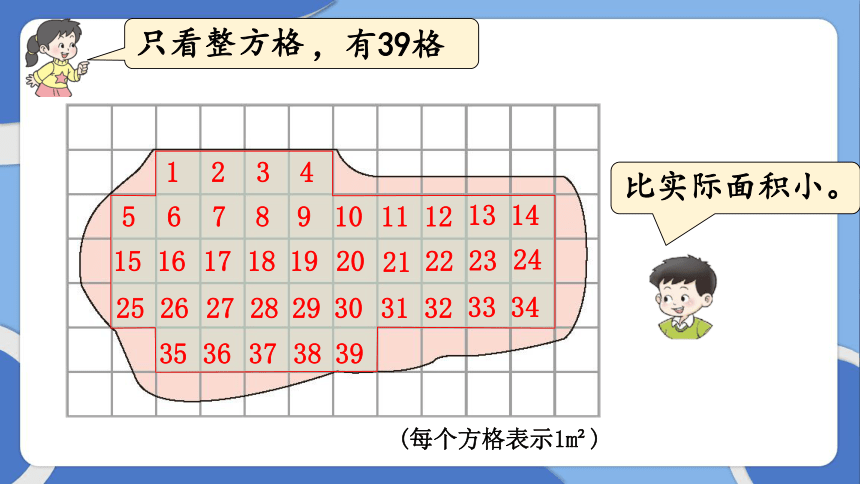
只看整方格
(每个方格表示1m )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
,有39格
比实际面积小。
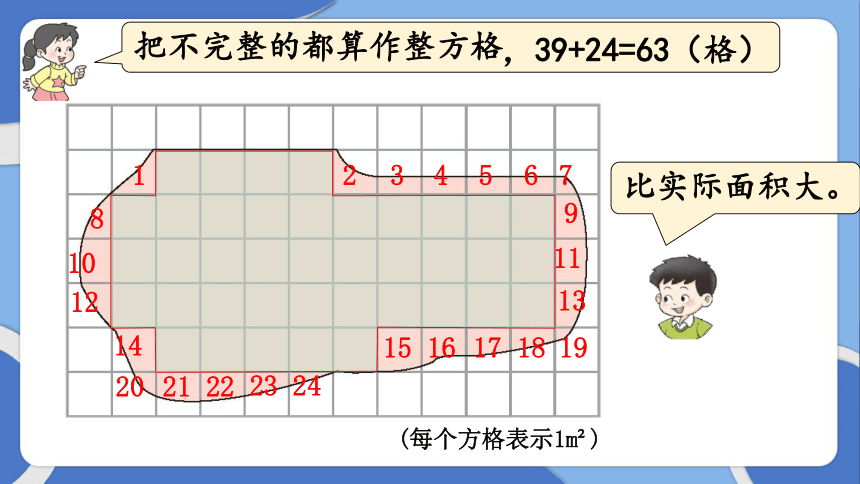
把不完整的都算作整方格
(每个方格表示1m )
,39+24=63(格)
比实际面积大。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(每个方格表示1m )
实验田的面积在39至63平方米之间。
一般情况下,不完整的方格看作半格。
24÷2=12
答:实验田大约有51m 。
39+12 = 51(m )
(每个方格表示1m )
(4个方格表示1m )
完整方格数:180个
方格越分越小,我们能确定的图形面积越来越多,估算的结果更接近实际面积
数学文化
很早以前,各国的数学家们一直在思考,如何计算出不规则地图的面积。许多国家的边界线受到自然环境等方面的影响,如同蚯蚓般曲折蜿蜒。多年来,大家一直寻找不到标准的计算方法,一般都是大致估算一下,粗略地取个近似值。
我国有一位木匠,他就是农民数学家于振善,听到这个问题后,专心致志地研究起来。经过多次实践,他终于找到了一种计算不规则图形面积的方法-“称法”,巧妙地称出了我国各行政区域的面积:
先精选一块质量、密度均匀的木板,根据木板总质量算出1cm 的质量。把各种不规则的地图剪贴在木板上,分别把这些图锯下来,用秤称出每块图板的质量。最后,用图板的质量除以木板单位面积也就是每平方厘米的质量,就不难求出每块图板所表示的实际面积了,也就是说,图板的质量中含有多少个1cm 的质量,就表示多少平方厘米,再扩大一定的倍数,就可以算出实际面积是多大了。
称面积
估计下面残缺地砖的面积。(每个方格表示1 dm 。)
试一试
完整:3
1
2
3
4
5
不完整:5
3+5÷2=5.5(dm )
完整:2
1
2
3
4
不完整:4
2+4÷2 =4(dm )
1
2
3
4
5
完整:7
不完整:5
7+5÷2=9.5(dm )
1.下面这块田的面积大约有多少平方米?(每个方格表示1m 。)
55+26÷2=68(m )
答:这块田的面积大约有68m 。
(教材第89页“练习二十二”第1题)
课堂练习
面积大
提示:两个图中方格大小相同,因此方格数多的面积大。
2.下面两个小岛,谁的面积大
(教材第89页“练习二十二”第2题)
通过这节课的学习,同学们有些什么收获呢?
课堂小结
不规则图形的面积
西师版小学数学五年级上册第五单元
课前导入
口算下列图形的面积,再说说它们的面积公式。
(单位:厘米)
3
13
8
8
11
3
10
6
6
5
9
探究新知
丽丽家里有一块地砖,她想算出这块地砖的
面积约是多少平方分米?
例
4分米
2分米
每个方格表示1dm
方法一:转化成规则图形
方法二:数方格
探究新知
实验田大约有多大?
例
(每个方格表示1m )
把实验田图纸放在透明的方格纸下,数方格。
探究新知
小组合作:
①学生独立完成,组内交流自己数方格的方法(优势和不足)
②如何验证自己的估算结果是否合理?
③小组内形成一种数方格的方法。
④组内选出1名代表,上台展示,时间5分钟。
只看整方格
(每个方格表示1m )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
,有39格
比实际面积小。
把不完整的都算作整方格
(每个方格表示1m )
,39+24=63(格)
比实际面积大。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(每个方格表示1m )
实验田的面积在39至63平方米之间。
一般情况下,不完整的方格看作半格。
24÷2=12
答:实验田大约有51m 。
39+12 = 51(m )
(每个方格表示1m )
(4个方格表示1m )
完整方格数:180个
方格越分越小,我们能确定的图形面积越来越多,估算的结果更接近实际面积
数学文化
很早以前,各国的数学家们一直在思考,如何计算出不规则地图的面积。许多国家的边界线受到自然环境等方面的影响,如同蚯蚓般曲折蜿蜒。多年来,大家一直寻找不到标准的计算方法,一般都是大致估算一下,粗略地取个近似值。
我国有一位木匠,他就是农民数学家于振善,听到这个问题后,专心致志地研究起来。经过多次实践,他终于找到了一种计算不规则图形面积的方法-“称法”,巧妙地称出了我国各行政区域的面积:
先精选一块质量、密度均匀的木板,根据木板总质量算出1cm 的质量。把各种不规则的地图剪贴在木板上,分别把这些图锯下来,用秤称出每块图板的质量。最后,用图板的质量除以木板单位面积也就是每平方厘米的质量,就不难求出每块图板所表示的实际面积了,也就是说,图板的质量中含有多少个1cm 的质量,就表示多少平方厘米,再扩大一定的倍数,就可以算出实际面积是多大了。
称面积
估计下面残缺地砖的面积。(每个方格表示1 dm 。)
试一试
完整:3
1
2
3
4
5
不完整:5
3+5÷2=5.5(dm )
完整:2
1
2
3
4
不完整:4
2+4÷2 =4(dm )
1
2
3
4
5
完整:7
不完整:5
7+5÷2=9.5(dm )
1.下面这块田的面积大约有多少平方米?(每个方格表示1m 。)
55+26÷2=68(m )
答:这块田的面积大约有68m 。
(教材第89页“练习二十二”第1题)
课堂练习
面积大
提示:两个图中方格大小相同,因此方格数多的面积大。
2.下面两个小岛,谁的面积大
(教材第89页“练习二十二”第2题)
通过这节课的学习,同学们有些什么收获呢?
课堂小结
