2024年九年级人教版数学上册综合训练寒假作业(能力培优提升篇)(含简单答案)
文档属性
| 名称 | 2024年九年级人教版数学上册综合训练寒假作业(能力培优提升篇)(含简单答案) | 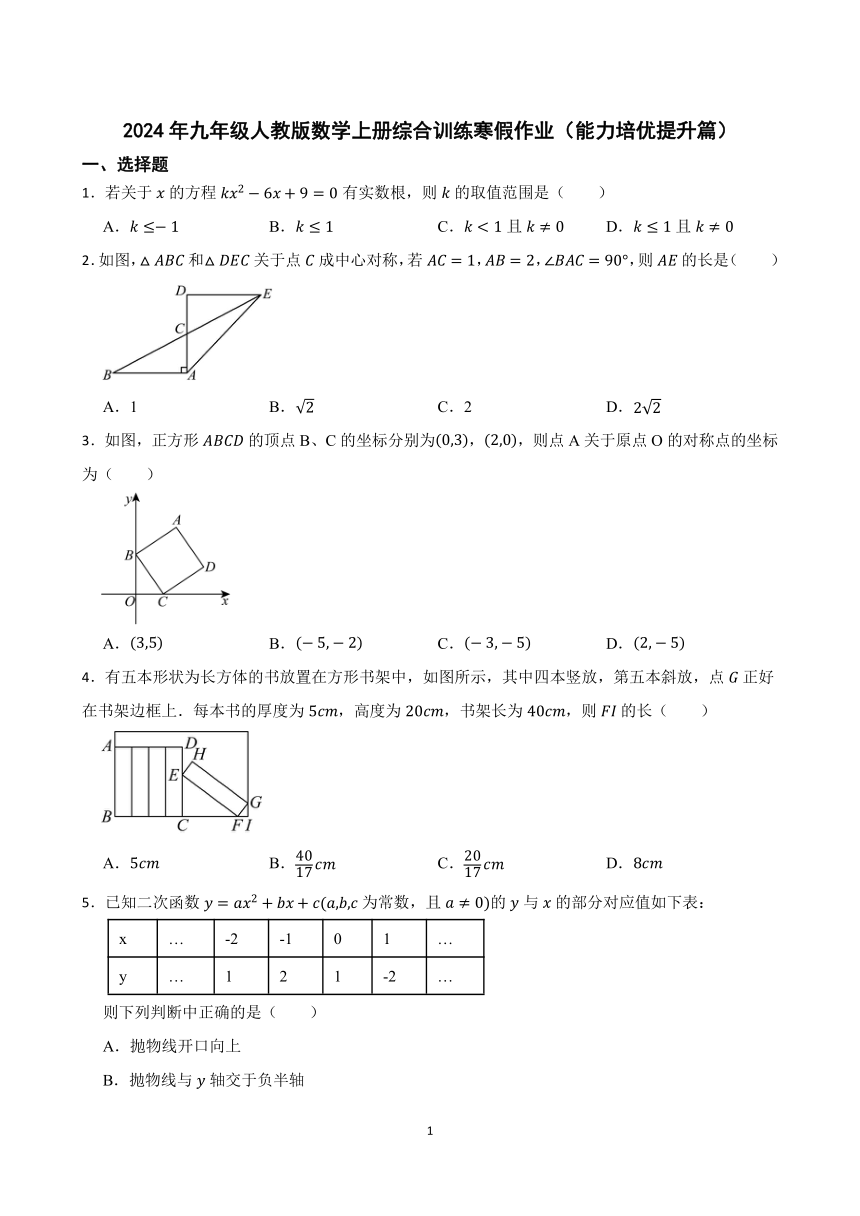 | |
| 格式 | docx | ||
| 文件大小 | 504.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-15 23:04:39 | ||
图片预览





文档简介
2024年九年级人教版数学上册综合训练寒假作业(能力培优提升篇)
一、选择题
1.若关于的方程有实数根,则的取值范围是( )
A. B. C.且 D.且
2.如图,和关于点成中心对称,若,,,则的长是( )
A.1 B. C.2 D.
3.如图,正方形的顶点B、C的坐标分别为,,则点A关于原点O的对称点的坐标为( )
A. B. C. D.
4.有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点正好在书架边框上.每本书的厚度为,高度为,书架长为,则的长( )
A. B. C. D.
5.已知二次函数为常数,且的与的部分对应值如下表:
x … -2 -1 0 1 …
y … 1 2 1 -2 …
则下列判断中正确的是( )
A.抛物线开口向上
B.抛物线与轴交于负半轴
C.当时,
D.方程的正根在0与1之间
6.如图所示,拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为米时,水面的宽度为( )
A.米 B.米 C.米 D.米
7.抛物线的部分图像如图所示,对称轴为直线,直线与抛物线都经过点.下列说法:①;②;③若与是抛物线上的两个点,;④方程的两根为,;⑤当时,函数有最大值.其中正确的个数是( )
A.2 B.3 C.4 D.5
8.如图,在正方形纸片中,点M,N在上,将纸片沿折叠,折叠后使点A和点D重合于点I,的外接圆分别交于点P,Q.若,则的长度为( )
A. B. C. D.
9.如图,在扇形中,平分交于点,点为半径上一动点.若,则阴影部分周长的最小值为( )
A. B. C. D.
10.我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图,若,,现随机向该图形内掷一枚小针,则针尖落在阴影区域内的概率( ).
A. B. C. D.
二、填空题
11.已知实数m,n满足,,且,若,则代数式的最小值是 .
12.若数使关于的不等式组有且只有四个整数解,且使关于的一元二次方程有实数根,则符合条件的所有整数的和为 .
13.如图,抛物线与轴交于点、,与轴交于点,点是抛物线上的动点,连接、,与轴交于点.过点作轴的平行线交轴于点,交直线于点,若,求的值为 .
14.已知二次函数的图像经过点与,关于的方程有两个根,其中一个根是5,若关于的方程有两个整数根,则这两个整数根分别是 .
15.如图,中,,点是边上一点,将绕点顺时针旋转到,连接,则长的最小值是 .
16.如图,在中,,以为直径的交于点,点是的中点,连接、,交于点,,,则 ,的值是 .
17. 如图, A B 为 的直径, 且 , 点 为 上半圆的一点, 于点 , 的角平分线交 于点 , 弦 , 那么 的面积是 .
18.有三张正面分别标有数字,,的不透明卡片,它们除数字不同外其余全部相同现将它们背面朝上,洗匀后从中任意抽取一张,将该卡片正面上的数字记为;不放回,再从中任意抽取一张,将该卡片正面朝上的数字记为,则使关于的不等式组的解集中有且只有个非负整数的概率为 .
三、计算题
19.解方程:
(1); (2).
20.已知关于x的一元二次方程.
(1)已知是此方程的一个根,求方程的另一个根及k的值;
(2)若此方程有两个相等的实数根,求实数k的值
21.已知二次函数,(p为实数)
(1)若函数与x轴交于不同的两点,,,求实数p的取值范围.
(2)若,,是方程的两根,当函数的图像分别与直线相交于A,B两点,与直线相交于C,D两点,当时,求p的值.
(3)若关于x方程有4个不相等的实数根,求p的取值范围.
四、解答题
22.如图,点O是等边内的一点,,将绕点C顺时针旋转得到,连接、.
(1)求的度数;
(2)若,,求的长.
23.某产品每件成本为20元,经过市场调研发现,这种产品在未来20天内的日销售量(单位:件)是关于时间(单位:天)的一次函数,调研所获的部分数据如下表:
时间/天 1 3 10 20
日销售量/件 98 94 80 60
这20天中,该产品每天的价格(单位:元/件)与时间的函数关系式为:(为整数),根据以上提供的条件解决下列问题:
(1)直接写出关于的函数关系式;
(2)这20天中哪一天的日销售利润最大,最大的销售利润是多少?
(3)在实际销售的20天中,每销售一件商品就捐赠元()给希望工程,通过销售记录发现,这20天中,每天扣除捐赠后的日销利润随时间的增大而增大,求的取值范围.
24.某商场推出购物摸球返现活动,在不透明的箱子中装有3个形状大小完全一样的小球,小球上分别印着“10元”“20元”“30元”的字样.规定顾客一次性消费满200元就可以参与摸球返现活动,摸中多少返现多少.
(1)小聪有1次摸球机会,求他摸中“30元”小球的概率;
(2)小明有2次摸球机会,请用列表法或画树状图的方法求出他2次摸球得到的返现金额之和超过30元的概率.
25.如图,已知二次函数图象的顶点为A,与y轴交于点B,异于顶点A的点在该函数图象上.
(1)①当时,求n的值.
②在①的条件下,当时,求y的最大值和最小值.
(2)当时,若点A在第一象限内,结合图象,求当时,自变量x的取值范围.
(3)作直线与y轴相交于点D,当点B在x轴上方,且在线段上时,直接写出m的取值范围.
26.综合与探究
如图,抛物线与坐标轴交于,,三点,其中点和点的坐标分别为和.
(1)求抛物线的解析式.
(2)求线段的长.
(3)如图2,P为抛物线第三象限上的一个动点,过点P作轴,交y轴于点H,连接,,与y轴交于点D.设点P的横坐标为t,的面积为S,求S与t之间的函数关系式(不用写出t的取值范围),并直接写出当时,S的值.
27.如图,是的内接三角形,是的直径,,,请解答下列问题:
(1)求的度数;
(2)设、相交于,、的延长线相交于,求、的度数;
(3)若,求图中阴影部分的面积.
28.如图,已知抛物线与x轴交于A、B(A在B的左边),与y轴交于C,且.
(1)若点A的坐标是,C的坐标是,试求抛物线的解析式;
(2)在(1)的条件下,如图1,直线与抛物线交于D、E两点,点F在直线下方的抛物线上,若以F为圆心作,满足与直线相切,求当的半径最大时,点F的坐标;
(3)如图2,若,M、N分别是抛物线对称轴右侧上的两点(M在N的右边),连接、、,交x轴于点P,点K是的中点,若的内心在x轴上,K的纵坐标为n,试探究的值是否为定值,若是,求出这个定值;若不是,请说明理由.
答案
1-10 BDCBD ABBAC
11.3
12.0
13.
14.4或-2
15.2.5
16.;
17.85
18.
19.(1),
(2),
20.(1),方程的另一个根是
(2)
21.(1)
(2)
(3)或
22.(1)
(2)
23.(1);(2)在第15天时日销售利润最大,最大利润为612.5元;(3).
24.(1)他摸中“30元”小球的概率为;
(2).
25.(1)①;②y的最大值为4,最小值为
(2)或
(3)或
26.(1)
(2)
(3);
27.(1)
(2),
(3)
28.(1)
(2)
(3)定值,
一、选择题
1.若关于的方程有实数根,则的取值范围是( )
A. B. C.且 D.且
2.如图,和关于点成中心对称,若,,,则的长是( )
A.1 B. C.2 D.
3.如图,正方形的顶点B、C的坐标分别为,,则点A关于原点O的对称点的坐标为( )
A. B. C. D.
4.有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点正好在书架边框上.每本书的厚度为,高度为,书架长为,则的长( )
A. B. C. D.
5.已知二次函数为常数,且的与的部分对应值如下表:
x … -2 -1 0 1 …
y … 1 2 1 -2 …
则下列判断中正确的是( )
A.抛物线开口向上
B.抛物线与轴交于负半轴
C.当时,
D.方程的正根在0与1之间
6.如图所示,拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为米时,水面的宽度为( )
A.米 B.米 C.米 D.米
7.抛物线的部分图像如图所示,对称轴为直线,直线与抛物线都经过点.下列说法:①;②;③若与是抛物线上的两个点,;④方程的两根为,;⑤当时,函数有最大值.其中正确的个数是( )
A.2 B.3 C.4 D.5
8.如图,在正方形纸片中,点M,N在上,将纸片沿折叠,折叠后使点A和点D重合于点I,的外接圆分别交于点P,Q.若,则的长度为( )
A. B. C. D.
9.如图,在扇形中,平分交于点,点为半径上一动点.若,则阴影部分周长的最小值为( )
A. B. C. D.
10.我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图,若,,现随机向该图形内掷一枚小针,则针尖落在阴影区域内的概率( ).
A. B. C. D.
二、填空题
11.已知实数m,n满足,,且,若,则代数式的最小值是 .
12.若数使关于的不等式组有且只有四个整数解,且使关于的一元二次方程有实数根,则符合条件的所有整数的和为 .
13.如图,抛物线与轴交于点、,与轴交于点,点是抛物线上的动点,连接、,与轴交于点.过点作轴的平行线交轴于点,交直线于点,若,求的值为 .
14.已知二次函数的图像经过点与,关于的方程有两个根,其中一个根是5,若关于的方程有两个整数根,则这两个整数根分别是 .
15.如图,中,,点是边上一点,将绕点顺时针旋转到,连接,则长的最小值是 .
16.如图,在中,,以为直径的交于点,点是的中点,连接、,交于点,,,则 ,的值是 .
17. 如图, A B 为 的直径, 且 , 点 为 上半圆的一点, 于点 , 的角平分线交 于点 , 弦 , 那么 的面积是 .
18.有三张正面分别标有数字,,的不透明卡片,它们除数字不同外其余全部相同现将它们背面朝上,洗匀后从中任意抽取一张,将该卡片正面上的数字记为;不放回,再从中任意抽取一张,将该卡片正面朝上的数字记为,则使关于的不等式组的解集中有且只有个非负整数的概率为 .
三、计算题
19.解方程:
(1); (2).
20.已知关于x的一元二次方程.
(1)已知是此方程的一个根,求方程的另一个根及k的值;
(2)若此方程有两个相等的实数根,求实数k的值
21.已知二次函数,(p为实数)
(1)若函数与x轴交于不同的两点,,,求实数p的取值范围.
(2)若,,是方程的两根,当函数的图像分别与直线相交于A,B两点,与直线相交于C,D两点,当时,求p的值.
(3)若关于x方程有4个不相等的实数根,求p的取值范围.
四、解答题
22.如图,点O是等边内的一点,,将绕点C顺时针旋转得到,连接、.
(1)求的度数;
(2)若,,求的长.
23.某产品每件成本为20元,经过市场调研发现,这种产品在未来20天内的日销售量(单位:件)是关于时间(单位:天)的一次函数,调研所获的部分数据如下表:
时间/天 1 3 10 20
日销售量/件 98 94 80 60
这20天中,该产品每天的价格(单位:元/件)与时间的函数关系式为:(为整数),根据以上提供的条件解决下列问题:
(1)直接写出关于的函数关系式;
(2)这20天中哪一天的日销售利润最大,最大的销售利润是多少?
(3)在实际销售的20天中,每销售一件商品就捐赠元()给希望工程,通过销售记录发现,这20天中,每天扣除捐赠后的日销利润随时间的增大而增大,求的取值范围.
24.某商场推出购物摸球返现活动,在不透明的箱子中装有3个形状大小完全一样的小球,小球上分别印着“10元”“20元”“30元”的字样.规定顾客一次性消费满200元就可以参与摸球返现活动,摸中多少返现多少.
(1)小聪有1次摸球机会,求他摸中“30元”小球的概率;
(2)小明有2次摸球机会,请用列表法或画树状图的方法求出他2次摸球得到的返现金额之和超过30元的概率.
25.如图,已知二次函数图象的顶点为A,与y轴交于点B,异于顶点A的点在该函数图象上.
(1)①当时,求n的值.
②在①的条件下,当时,求y的最大值和最小值.
(2)当时,若点A在第一象限内,结合图象,求当时,自变量x的取值范围.
(3)作直线与y轴相交于点D,当点B在x轴上方,且在线段上时,直接写出m的取值范围.
26.综合与探究
如图,抛物线与坐标轴交于,,三点,其中点和点的坐标分别为和.
(1)求抛物线的解析式.
(2)求线段的长.
(3)如图2,P为抛物线第三象限上的一个动点,过点P作轴,交y轴于点H,连接,,与y轴交于点D.设点P的横坐标为t,的面积为S,求S与t之间的函数关系式(不用写出t的取值范围),并直接写出当时,S的值.
27.如图,是的内接三角形,是的直径,,,请解答下列问题:
(1)求的度数;
(2)设、相交于,、的延长线相交于,求、的度数;
(3)若,求图中阴影部分的面积.
28.如图,已知抛物线与x轴交于A、B(A在B的左边),与y轴交于C,且.
(1)若点A的坐标是,C的坐标是,试求抛物线的解析式;
(2)在(1)的条件下,如图1,直线与抛物线交于D、E两点,点F在直线下方的抛物线上,若以F为圆心作,满足与直线相切,求当的半径最大时,点F的坐标;
(3)如图2,若,M、N分别是抛物线对称轴右侧上的两点(M在N的右边),连接、、,交x轴于点P,点K是的中点,若的内心在x轴上,K的纵坐标为n,试探究的值是否为定值,若是,求出这个定值;若不是,请说明理由.
答案
1-10 BDCBD ABBAC
11.3
12.0
13.
14.4或-2
15.2.5
16.;
17.85
18.
19.(1),
(2),
20.(1),方程的另一个根是
(2)
21.(1)
(2)
(3)或
22.(1)
(2)
23.(1);(2)在第15天时日销售利润最大,最大利润为612.5元;(3).
24.(1)他摸中“30元”小球的概率为;
(2).
25.(1)①;②y的最大值为4,最小值为
(2)或
(3)或
26.(1)
(2)
(3);
27.(1)
(2),
(3)
28.(1)
(2)
(3)定值,
同课章节目录
