天津市河东区2024-2025学年高三上学期期末质量检测试题 数学(含答案)
文档属性
| 名称 | 天津市河东区2024-2025学年高三上学期期末质量检测试题 数学(含答案) | 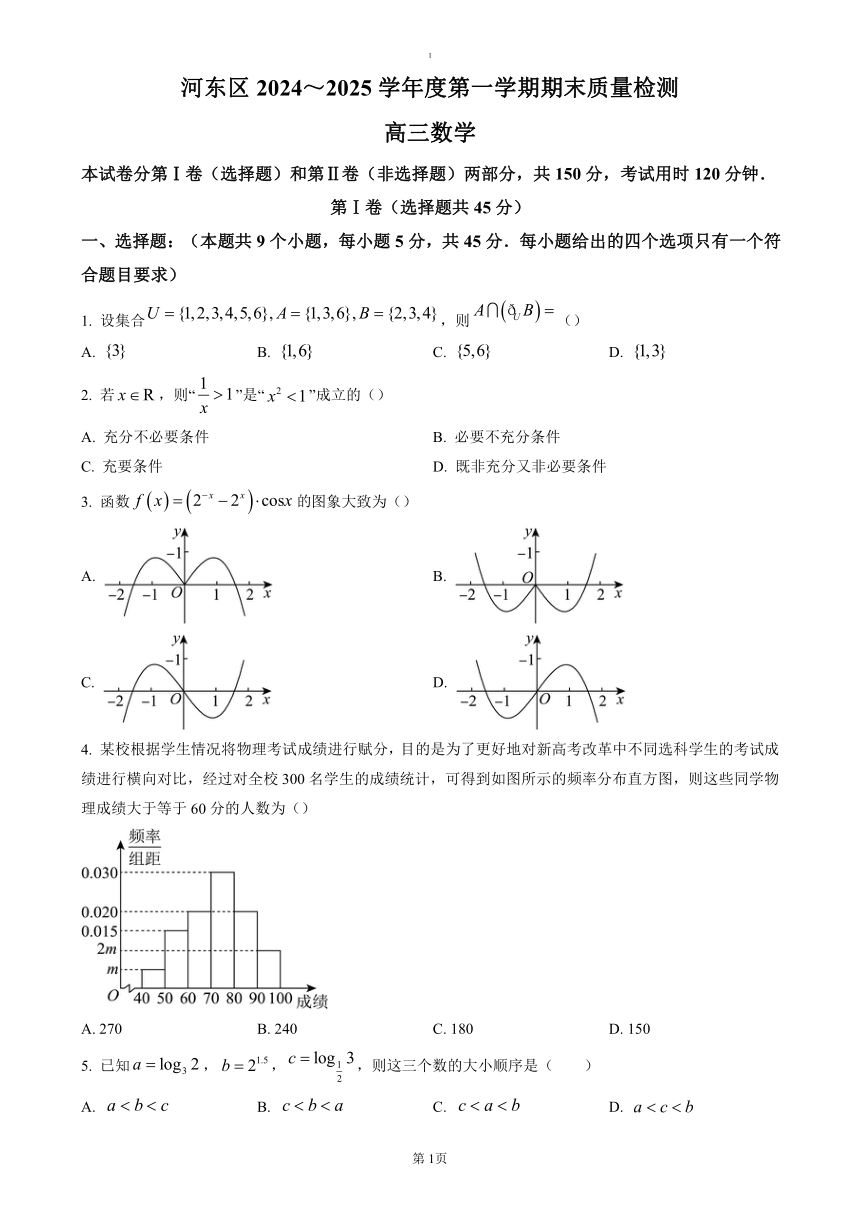 | |
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 18:37:40 | ||
图片预览





文档简介
1
河东区2024~2025学年度第一学期期末质量检测
高三数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.
第Ⅰ卷(选择题共45分)
一、选择题:(本题共9个小题,每小题5分,共45分.每小题给出的四个选项只有一个符合题目要求)
1. 设集合,则()
A. B. C. D.
2. 若,则“”是“”成立的()
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既非充分又非必要条件
3. 函数图象大致为()
A. B.
C. D.
4. 某校根据学生情况将物理考试成绩进行赋分,目的是为了更好地对新高考改革中不同选科学生的考试成绩进行横向对比,经过对全校300名学生的成绩统计,可得到如图所示的频率分布直方图,则这些同学物理成绩大于等于60分的人数为()
A. 270 B. 240 C. 180 D. 150
5. 已知,,,则这三个数的大小顺序是( )
A. B. C. D.
6. 如图,正三棱柱的底面边长为1,高为3,已知为棱的中点,分别在棱上,,记四棱锥,三棱锥与三棱锥的体积分别为,则()
A. B. C. D.
7. 已知函数,则下列说法中,正确的是()
A. 的最小值为
B. 在区间上单调递增
C. 的最小正周期为
D. 的图象可由的图象向右平移个单位得到
8. 抛物线的焦点是双曲线的右焦点,点是曲线的交点,点在抛物线的准线上,是以点为直角顶点的等腰直角三角形,则双曲线的离心率为
A B. C. D.
9. 已知且,则的最小值为()
A. B. C. D.
二、填空题(本大题共6个小题,每小题5分,共30分)
10. 已知为虚数单位,复数,则复数的虚部为________
11. 在展开式中,的系数是______.
12. 已知圆与抛物线的准线交于两点,且,则的值为______.
13. 某厂产品有的产品不需要调试就可以出厂上市,另的产品经过调试以后有能出厂,则该厂产品能出厂的概率______;任取一出厂产品,求未经调试的概率______.
14. 在等腰梯形中,,是腰的中点,则的值为______;若是腰上的动点,则的最小值为______.
15. 已知函数,若有三个不等零点,则实数的取值范围是______.
三、解答题:(本大题5个题,共75分)
16. 内角的对边分别为,已知,.
(1)求;
(2)若,求.
17. 如图,在四棱锥中,平面,,,,,为中点,点在线段上,且.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
(3)求平面与平面所成角的正弦值.
18. 已知椭圆一个顶点,以椭圆的四个顶点为顶点的四边形面积为.
(1)求椭圆E的方程;
(2)过点P(0,-3)的直线l斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与直线交于点M,N,当|PM|+|PN|≤15时,求k的取值范围.
19. 设是等差数列,是等比数列,公比大于0,已知,.
(1)求和的通项公式;
(2)设数列的前项和.记,求;
(3)求.
20. 已知函数与为函数的极值点.
(1)求的值;
(2)求在点处的切线方程;
(3)若恒成立,求实数取值范围.
河东区2024~2025学年度第一学期期末质量检测
高三数学
一、选择题:(本题共9个小题,每小题5分,共45分.每小题给出的四个选项只有一个符合题目要求)
1.
【答案】B
2.
【答案】A
3.
【答案】C
4.
【答案】B
5.
【答案】C
6.
【答案】C
7.
【答案】D
8.
【答案】A
9.
【答案】B
二、填空题(本大题共6个小题,每小题5分,共30分)
10.【答案】##
11.【答案】
12.【答案】4
13.
【答案】 ①. ②.
14.【答案】 ①. ②.
15.【答案】
三、解答题:(本大题5个题,共75分)
16.
【解】
【分析】(1)根据正余弦定理角化边即可得出答案;
(2)先利用余弦定理求出,再根据同角三角函数的关系求出,以及二倍角公式求出和,最后再根据正弦的差角公式即可得出答案.
【小问1详解】
因为,由余弦定理有:,所以;
因为,由正弦定理得:,所以,
所以.
【小问2详解】
因为,所以,
,
.
17.
【解】
【分析】(1)以为原点,建立空间直角坐标系,由已知写出、、的坐标,由点坐标可得,,的坐标,即有,,根据线面垂直的判定即可证平面;
(2)由已知点坐标及,可写出、的坐标,进而求面的一个法向量,根据直线方向向量与平面法向量夹角的坐标表示,求直线与平面所成角的正弦值;
(3)由坐标系易知为平面的法向量,结合(2)所得法向量,根据两个平面法向量夹角的坐标表示,即可求二面角的余弦值,进而求其正弦值.
【小问1详解】
证明:如图,以为原点,分别以,为轴,轴,过D作AP平行线为z轴,建立空间直角坐标系,
则,,,得,,,
所以,,即,,又,所以平面;
【小问2详解】
解:由可是,
由,可得,所以,
设为平面的法向量,
则不妨设,则,故,
设直线与平面所成角为,所以,
则直线与平面所成角的正弦值为;
【小问3详解】
解:因为为平面的法向量,设二面角的大小为,
所以,所以.则二面角的正弦值为.
18.
【解】
【分析】(1)根据椭圆所过的点及四个顶点围成的四边形的面积可求,从而可求椭圆的标准方程.
(2)设,求出直线的方程后可得的横坐标,从而可得,联立直线的方程和椭圆的方程,结合韦达定理化简,从而可求的范围,注意判别式的要求.
【详解】(1)因为椭圆过,故,
因为四个顶点围成的四边形的面积为,故,即,
故椭圆的标准方程为:.
(2)
设,
因为直线的斜率存在,故,
故直线,令,则,同理.
直线,由可得,
故,解得或.
又,故,所以
又
故即,
综上,或.
19.
【解】
【分析】(1)根据已知及等差、等比数列的通项公式求基本量,进而写出和的通项公式;
(2)根据已知有,结合(1)即可得;
(3)应用错位相减法、等比数列前n项和公式求和.
【小问1详解】
设数列是公差为d的等差数列,数列是公比为q的等比数列,公比大于0,其前n项和为.
已知,所以,解得,则,
由于,所以,,解得,则.
【小问2详解】
由(1)知:,所以,
所以.
【小问3详解】
由(2)得,设,
所以①,②,
①②得:,
整理得.
20.
【解】
【分析】(1)根据极值点与导数的关系,得,解得答案;
(2)根据导数的几何意义得出切线斜率,点斜式得切线方程;
(3)由参变分离得,利用导数求出函数的最小值,的答案.
【小问1详解】
由题意可为,的定义域为
因为在处取得极值,所以,解,
当时,单调递增;当时,单调递减,
经检验,符合题意,
所以.
【小问2详解】
所以切线方程为.
.
【小问3详解】
若恒成立,则,
由,
因为,所以,
令,则,
令,则,
所以在区间上单调递增,
因为,,
所以存在唯一,使得,
即,即
令,则,
所以函数在上单调递增,
因为,则,,由,
则,所以,
当时,,,单调递减,
当时,,单调递增,
所以,
则,
所以实数的取值范围为
PAGE
第1页
河东区2024~2025学年度第一学期期末质量检测
高三数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.
第Ⅰ卷(选择题共45分)
一、选择题:(本题共9个小题,每小题5分,共45分.每小题给出的四个选项只有一个符合题目要求)
1. 设集合,则()
A. B. C. D.
2. 若,则“”是“”成立的()
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既非充分又非必要条件
3. 函数图象大致为()
A. B.
C. D.
4. 某校根据学生情况将物理考试成绩进行赋分,目的是为了更好地对新高考改革中不同选科学生的考试成绩进行横向对比,经过对全校300名学生的成绩统计,可得到如图所示的频率分布直方图,则这些同学物理成绩大于等于60分的人数为()
A. 270 B. 240 C. 180 D. 150
5. 已知,,,则这三个数的大小顺序是( )
A. B. C. D.
6. 如图,正三棱柱的底面边长为1,高为3,已知为棱的中点,分别在棱上,,记四棱锥,三棱锥与三棱锥的体积分别为,则()
A. B. C. D.
7. 已知函数,则下列说法中,正确的是()
A. 的最小值为
B. 在区间上单调递增
C. 的最小正周期为
D. 的图象可由的图象向右平移个单位得到
8. 抛物线的焦点是双曲线的右焦点,点是曲线的交点,点在抛物线的准线上,是以点为直角顶点的等腰直角三角形,则双曲线的离心率为
A B. C. D.
9. 已知且,则的最小值为()
A. B. C. D.
二、填空题(本大题共6个小题,每小题5分,共30分)
10. 已知为虚数单位,复数,则复数的虚部为________
11. 在展开式中,的系数是______.
12. 已知圆与抛物线的准线交于两点,且,则的值为______.
13. 某厂产品有的产品不需要调试就可以出厂上市,另的产品经过调试以后有能出厂,则该厂产品能出厂的概率______;任取一出厂产品,求未经调试的概率______.
14. 在等腰梯形中,,是腰的中点,则的值为______;若是腰上的动点,则的最小值为______.
15. 已知函数,若有三个不等零点,则实数的取值范围是______.
三、解答题:(本大题5个题,共75分)
16. 内角的对边分别为,已知,.
(1)求;
(2)若,求.
17. 如图,在四棱锥中,平面,,,,,为中点,点在线段上,且.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
(3)求平面与平面所成角的正弦值.
18. 已知椭圆一个顶点,以椭圆的四个顶点为顶点的四边形面积为.
(1)求椭圆E的方程;
(2)过点P(0,-3)的直线l斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与直线交于点M,N,当|PM|+|PN|≤15时,求k的取值范围.
19. 设是等差数列,是等比数列,公比大于0,已知,.
(1)求和的通项公式;
(2)设数列的前项和.记,求;
(3)求.
20. 已知函数与为函数的极值点.
(1)求的值;
(2)求在点处的切线方程;
(3)若恒成立,求实数取值范围.
河东区2024~2025学年度第一学期期末质量检测
高三数学
一、选择题:(本题共9个小题,每小题5分,共45分.每小题给出的四个选项只有一个符合题目要求)
1.
【答案】B
2.
【答案】A
3.
【答案】C
4.
【答案】B
5.
【答案】C
6.
【答案】C
7.
【答案】D
8.
【答案】A
9.
【答案】B
二、填空题(本大题共6个小题,每小题5分,共30分)
10.【答案】##
11.【答案】
12.【答案】4
13.
【答案】 ①. ②.
14.【答案】 ①. ②.
15.【答案】
三、解答题:(本大题5个题,共75分)
16.
【解】
【分析】(1)根据正余弦定理角化边即可得出答案;
(2)先利用余弦定理求出,再根据同角三角函数的关系求出,以及二倍角公式求出和,最后再根据正弦的差角公式即可得出答案.
【小问1详解】
因为,由余弦定理有:,所以;
因为,由正弦定理得:,所以,
所以.
【小问2详解】
因为,所以,
,
.
17.
【解】
【分析】(1)以为原点,建立空间直角坐标系,由已知写出、、的坐标,由点坐标可得,,的坐标,即有,,根据线面垂直的判定即可证平面;
(2)由已知点坐标及,可写出、的坐标,进而求面的一个法向量,根据直线方向向量与平面法向量夹角的坐标表示,求直线与平面所成角的正弦值;
(3)由坐标系易知为平面的法向量,结合(2)所得法向量,根据两个平面法向量夹角的坐标表示,即可求二面角的余弦值,进而求其正弦值.
【小问1详解】
证明:如图,以为原点,分别以,为轴,轴,过D作AP平行线为z轴,建立空间直角坐标系,
则,,,得,,,
所以,,即,,又,所以平面;
【小问2详解】
解:由可是,
由,可得,所以,
设为平面的法向量,
则不妨设,则,故,
设直线与平面所成角为,所以,
则直线与平面所成角的正弦值为;
【小问3详解】
解:因为为平面的法向量,设二面角的大小为,
所以,所以.则二面角的正弦值为.
18.
【解】
【分析】(1)根据椭圆所过的点及四个顶点围成的四边形的面积可求,从而可求椭圆的标准方程.
(2)设,求出直线的方程后可得的横坐标,从而可得,联立直线的方程和椭圆的方程,结合韦达定理化简,从而可求的范围,注意判别式的要求.
【详解】(1)因为椭圆过,故,
因为四个顶点围成的四边形的面积为,故,即,
故椭圆的标准方程为:.
(2)
设,
因为直线的斜率存在,故,
故直线,令,则,同理.
直线,由可得,
故,解得或.
又,故,所以
又
故即,
综上,或.
19.
【解】
【分析】(1)根据已知及等差、等比数列的通项公式求基本量,进而写出和的通项公式;
(2)根据已知有,结合(1)即可得;
(3)应用错位相减法、等比数列前n项和公式求和.
【小问1详解】
设数列是公差为d的等差数列,数列是公比为q的等比数列,公比大于0,其前n项和为.
已知,所以,解得,则,
由于,所以,,解得,则.
【小问2详解】
由(1)知:,所以,
所以.
【小问3详解】
由(2)得,设,
所以①,②,
①②得:,
整理得.
20.
【解】
【分析】(1)根据极值点与导数的关系,得,解得答案;
(2)根据导数的几何意义得出切线斜率,点斜式得切线方程;
(3)由参变分离得,利用导数求出函数的最小值,的答案.
【小问1详解】
由题意可为,的定义域为
因为在处取得极值,所以,解,
当时,单调递增;当时,单调递减,
经检验,符合题意,
所以.
【小问2详解】
所以切线方程为.
.
【小问3详解】
若恒成立,则,
由,
因为,所以,
令,则,
令,则,
所以在区间上单调递增,
因为,,
所以存在唯一,使得,
即,即
令,则,
所以函数在上单调递增,
因为,则,,由,
则,所以,
当时,,,单调递减,
当时,,单调递增,
所以,
则,
所以实数的取值范围为
PAGE
第1页
同课章节目录
