7.5三角形内角和定理课件

课件16张PPT。第5节 三角形内角和定理（第1课时） 第七章 平行线的证明学习目标
知识与技能
掌握三角形内角和定理的证明及简单应用。
灵活运用三角形内角和定理解决相关问题。
过程与方法
用多种方法证明三角形内角和定理，培养
一题多解的能力。
情感、态度与价值观
对比过去撕纸等探索过程，体会思维实验
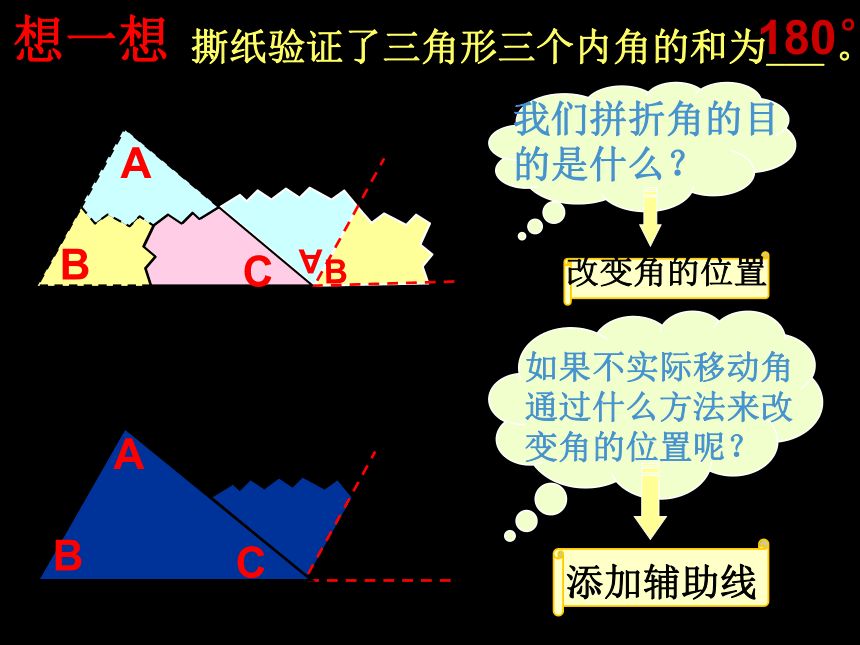
和符号化推理之间的联系。 如果不实际移动角通过什么方法来改变角的位置呢？ A B我们拼折角的目的是什么？改变角的位置添加辅助线想一想撕纸验证了三角形三个内角的和为___ 。180°回顾与思考1、根据题意，画出图形；
2、根据题设、结论、结合图形，
写出已知，求证；
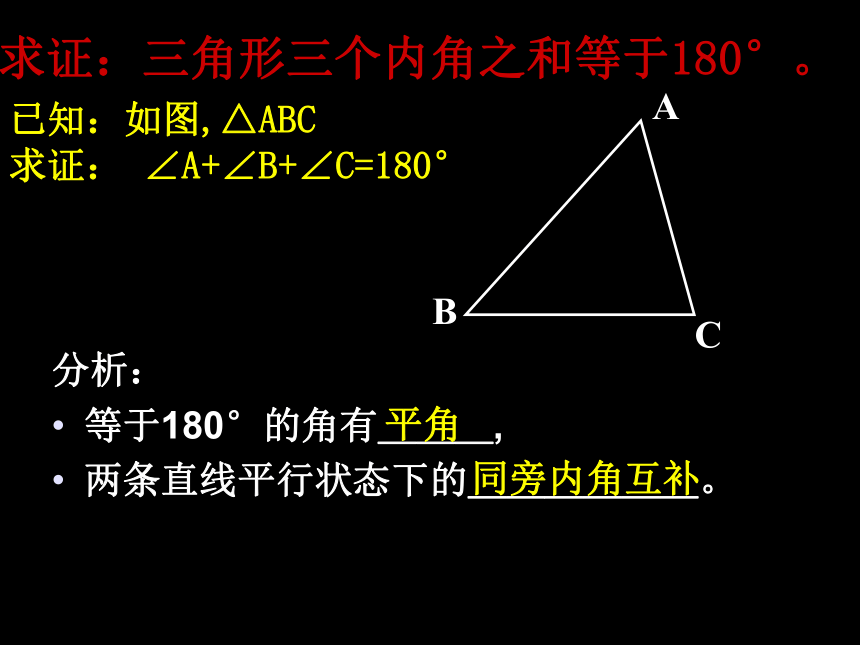
3、经过分析，写出证明过程。我们猜想,任意一个三角形的内角和等于180°.怎么验证猜想是对的呢?证明命题的一般步骤：求证：三角形三个内角之和等于180°。已知：如图,△ABC
求证： ∠A+∠B+∠C=180° 分析：
等于180°的角有＿＿＿,
两条直线平行状态下的＿＿＿＿＿＿。平角同旁内角互补
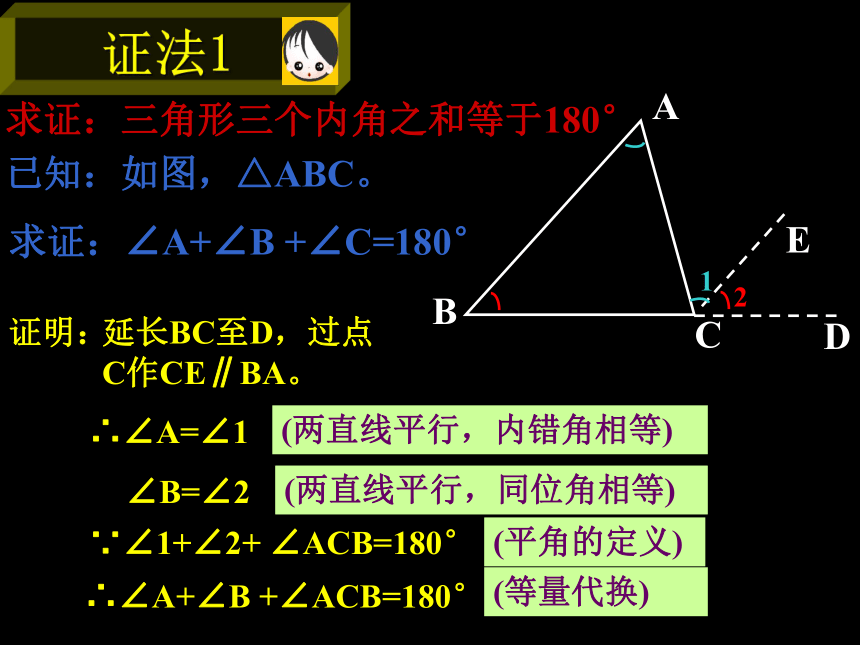
∴∠A=∠1 (两直线平行，内错角相等)延长BC至D，过点
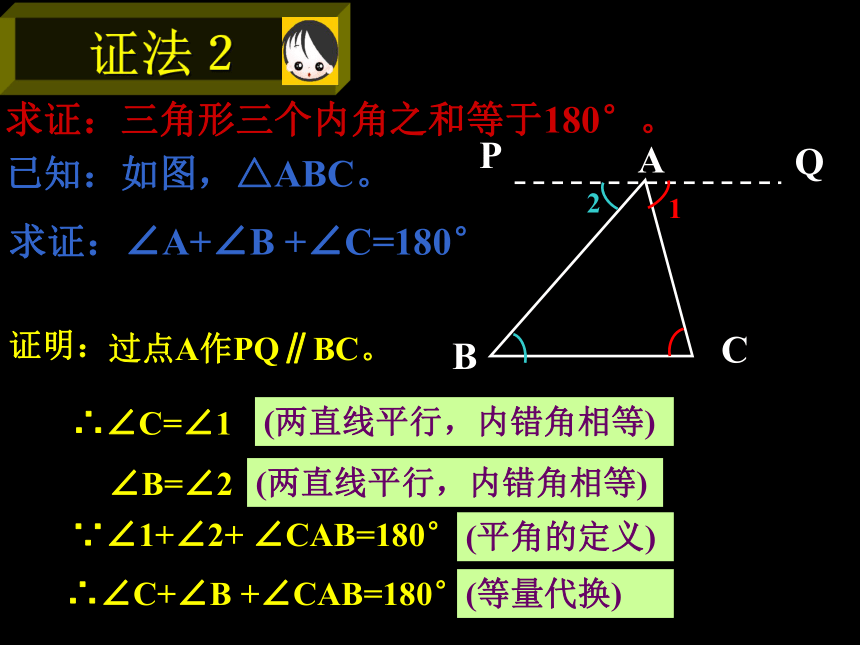
C作CE∥BA。∵∠1+∠2+ ∠ACB=180°(平角的定义)∴∠A+∠B +∠ACB=180°(等量代换) ∠B=∠2 (两直线平行，同位角相等)DE已知：如图，△ABC。求证：∠A+∠B +∠C=180°证明：求证：三角形三个内角之和等于180°已知：如图，△ABC。求证：∠A+∠B +∠C=180° 证明：∴∠C=∠1 (两直线平行，内错角相等)过点A作PQ∥BC。∵∠1+∠2+ ∠CAB=180°(平角的定义)∴∠C+∠B +∠CAB=180°(等量代换)ABC ∠B=∠2 (两直线平行，内错角相等)PQ求证：三角形三个内角之和等于180°。证明：过A作AE∥BC，∴∠C=∠CAE(两直线平行,内错角相等) ∠EAC+∠BAC+∠B=180°(两直线平行,同旁内角互补)∴∠C+∠BAC+∠B=180°(等量代换)已知：如图，△ABC。求证：∠A+∠B +∠C=180°求证：三角形三个内角之和等于180°“行家”看“门道”根据下面的图形,写出相应的证明.BCAA 求出下列图中x的值: x °x °x °x °x °2 x ° x °┐ x ° 150°┐20°130 °45 °练习 1 如图所示，求?1的度数？练习 2 如图，?A1+?A2+?A3+?A4+?A5 的度数。已知：如图，在△ABC中，∠A=105°，∠B
=50°，将∠C折起，点C落在△ABC内部，已知∠1=20°，求∠2的大小。求证：四边形的内角和等于360°1、2、今天的收获： 证明三角形内角和定理的几种方法 三角形内角和定理的简单应用 辅助线的作法技巧 数学中的转化思想只有一条路不能选择
——那就是放弃的路；
只有一条路不能拒绝
——那就是成长的路。再努力！还有更大的惊喜哦！敬请各位提出宝贵意见，谢谢！