3.2图形的旋转课件

课件43张PPT。3.2图形的旋转
教学目标通过观察具体事例认识旋转，探索它的基本性质。扇叶车轮水轮动感的旋转世界 齿轮使用扳手拧螺丝指南针地球自转荡秋千旋转的运动单杠翘翘板世界如此美丽雪花紫荆花会徽这些图案有什么共同特征？车标观 察 钟表的指针在不停地转动，从12时到4时，时针转动了______度。120° 把时针当成一个图形，那么它可以绕着中心固定点转动一定角度。 怎样来定义这种图形变换？观 察 风车风轮的每个叶片在风的吹动下转动到新的位置。 怎样来定义这种图形变换？ 把叶片当成一个图形，那么它可以绕着中心固定点转动一定角度。
（１）上面情景中的转动现象，有什么共同的特征？
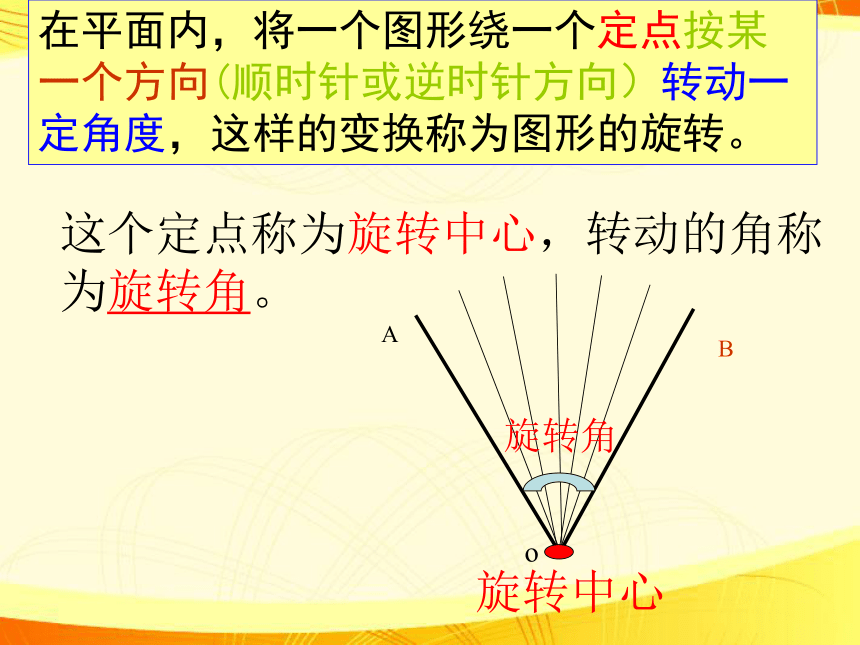
（２）钟表的指针、秋千在转动过程中，其形状、大小、位置是否发生变化呢？这个定点称为旋转中心，转动的角称为旋转角。在平面内，将一个图形绕一个定点按某一个方向(顺时针或逆时针方向）转动一定角度，这样的变换称为图形的旋转。AoB归纳定义 把一个图形绕着某一定点O按某一个方向转动一个角度这样的图形变换叫做旋转．这个定点O叫旋转中心，转动的角叫做旋转角． 如果图形上的点P经过旋转变为点P′，那么这两个点P和P′叫做这个旋转的对应点. 动态演示OP′P 若叶片 A 绕 O 顺时针旋转到叶片 B，则旋转中心是______，旋转角是_________，旋转角等于____度，其中的对应点有_______、 _______、 _______、 _______、 _______、 _______ 。ABCDEFO 抢答O∠AOB60F与AA与BB与CC与DD与EE与F 杠杆绕支点转动撬起重物，杠杆的旋转中心就____，旋转角是_______________________。BOB′AA′∠AOA′ O∠BOB′ 或BOA点A绕___点沿_______方向，转动了___度到点 B。Ｏ顺时针45把小孩看作一个质点来分析问题秋千的固定点旋转的三要素 旋转中心 旋转方向 旋转角度OAA′A'B'BAAO·BB′O·A'动手画一画1.画出将点P绕点O按顺时针方向旋转900后的点P′.AO·POＰ′BA′B′2.画出线段AB绕点O按顺时
　针方向旋转90０后的图形.　BACOB′C′A′动手画一画3.画出将△ABC绕点O按顺时针方向旋转900后的对应三角形。　OBABAB′A′CC′O 点A、线段AB、∠ABC分别旋转到了什么位置？点A′点A线段A′B′∠A′ B′ C′对应点对应边对应角观 察 在上面两个实验中，△ABC在旋转过程中，哪些发生了变化？归纳 各点的位置发生变化。点A′点A点B′点B点C′点C 从而，各线段、各角的位置发生变化。OA=OA′OB=OB′OC=OC′ 边的相等关系：AB=A′B′BC=B′C′CA=C′A′对应边相等 在上面两个实验中，△ABC在旋转过程中，哪些没有改变？ 角的相等关系：∠ABC=∠A′B′C′ ∠AOA ′=∠BOB ′=∠COC ′ ∠BCA=∠B′C′A′ ∠CAB=∠C′A′B′ 对应角相等= 旋转角注：图形中每一点都绕着旋转中心旋转了同
样大小的角度。 对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
旋转前、后的图形全等。
图形的旋转是由旋转中心和旋转角决定。
图形的旋转不改变图形的形状、大小，只改变图形的位置。旋转的基本性质AO将A点绕O沿顺时针方向旋转60?。 作法：
1. 以O为圆心，OA长为半径画圆;
2. 连接OA，用量角器或三角板（限特殊角）作出∠AOB，与圆周交于B点；
3. B点即为所求作。B点的旋转作法AO 将线段AB绕O沿顺时针方向旋转60?。 作法：
1. 将点A绕点O顺时针旋转60?，得点aC;
2. 将点B绕点O顺时针旋转60 ?，得点D ；
3. 连接CD, 则线段CD即为所求作.CBD线段的旋转作法 已知△OAB，画出△OAB绕点O逆时针旋转100°后的图形。BAO 1. 连接OA。 2. 作∠AOC=100°，在OC上截取OA′=OA 。 4. 作∠BOD=100°，
在OD上截OB′=OB 。CD 3. 连接OB 。注：作旋转后的图形可以转化为作旋转后的对应点。图形的旋转作法 5. 连接A′B′，则△OA′B′即为所求作。作法： 四边形ABCD是边长为1的正方形，且DE= ，△ABF是△ADE的旋转图形。
（1）旋转中心是哪一点？
（2）旋转了多少度？
（3）AF的长度是多少？
（4）如果连结EF，那么△AEF是怎样的三角形？点A 。（2）∵ △ABF是由△ADE旋转而得的，
∴ B是D的对应点。
∴ ∠DAB是旋转角，答：∴ ∠DAB = 90°，即旋转了90°。ABCDEF（3）∵AD=1，DE=
∴
∵ AF 是AE 的对应边
∴ AF = AE =？（勾股定理）（对应边相等）（4）∵ ∠EAF=90°（与旋转角相等）
且 AF=AE（对应边相等）
∴△EAF是等腰直角三角形。 因此，选择不同的旋转角，不同的旋转中心，会出现不同的效果，我们可以经过旋转，设计出美丽的图案。 归纳 1. 钟表的分针匀速旋转一周需要60分。
（１）指出它的旋转中心；
（２）经过20分，分针旋转了多少度？ 随堂练习 (第5题)2.如图，△ABC为等边三角形，D是△ABC内一点，若将△ABD经过旋转后到△ACP位置，则旋转中心是__________，旋转角等于_________度，△ADP是___________三角形.A60等边3.如图，用左面的三角形经过怎样旋转，可以得到右面的图形．4.找出图中扳手拧螺母时的旋转中心和旋转角．OAB 5. 四边形AOBC 绕O点旋转得到四边形DOEF. 在这个旋转过程中：
（1）旋转中心是什么?
（2）经过旋转，点A、B分别移动到什么位置？
（3）旋转角是什么？
（4）AO与DO的长有什么关系？BO与EO呢？
（5）∠AOD与∠BOE有
什么大小关系？旋转中心是O点D和点E的位置AO=DO，BO=EO∠AOD=∠BOE∠AOD和∠BOE都是BACODEFABCDEF 6. 如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心。 旋转中心在对应点连线的垂直平分线上。O 7. K是正方形ABCD内一点，以AK为一边作正方形AKLM，使L、M在AK的同旁，连接BK和DM，试用旋转的思想说明线段BK与DM的关系。 解：∵四边形ABCD、四边形AKLM是正方形
∴AB=AD，AK=AM，且∠BAD=∠KAM为旋转角且为90°
∴△ADM是以A为旋转中心，∠BAD为旋转角由△ABK旋转而成的
∴BK=DM 8. P是等边?ABC内的一点，把?ABP按不同的方向通过旋转得到?BQC和?ACR，
（1）指出旋转中心、旋转方向和旋转角度？
（2） ?ACR是否可以直接通过把?BQC旋转得到？课堂回顾：这节课，主要学习了什么？在平面内，将一个图形绕着一个定点沿某个方向转动一个角度，这样的图形运动称为旋转旋转的概念：旋转的性质：1、旋转不改变图形的大小和形状．2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角，旋转角相等．3、对应点到旋转中心的距离相等平移和旋转的异同：
1、相同：都是一种运动；运动前后 不改变图形的形状和大小BACO2、不同