6.1平行四边形的性质课件(14张ppt)
文档属性
| 名称 | 6.1平行四边形的性质课件(14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-20 00:00:00 | ||
图片预览








文档简介
课件20张PPT。北师大版八年级数学(下)第六章 平行四边形第一节 平行四边形的性质1第一节 平行四边形的性质1学习目标:
1.探索交流平行四边形的有关概念和性质。
2.理解并掌握平行四边形的性质,能运用这些性
质解决简单的问题。
3.在相关的学习活动中主动探究讨论,学会与他
人合作交流。 美丽的家园,我们要好好的利用和保护她中国的骄傲,我们学习的榜样!我们的校园,学习的乐园美观别致 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?做一做1从拼图可以得到什么启示?小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题。观察拼出的这些平行四边形的对边有怎样的位置关系?为什么?1.定义:两组对边__________的四边形叫平形四边形。 一、平行四边形的相关概念分别平行几何语言:∵AB//CD,BC//AD
∴四边形ABCD是平行四边形反过来,∵四边形ABCD是平行四边形
∴AB//CD,BC//AD2、平行四边形不相邻的两个顶点连成的线段叫它的对角线。3、平行四边形相对的边称为 对边;
相对的角称为 对角;
相邻的角称为 邻角。
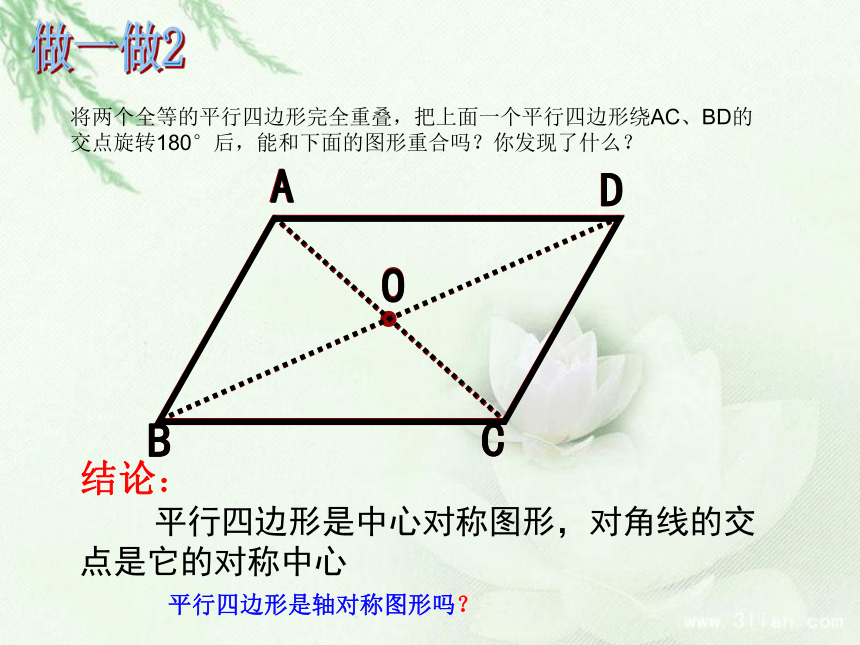
结论:
平行四边形是中心对称图形,对角线的交 点是它的对称中心做一做2将两个全等的平行四边形完全重叠,把上面一个平行四边形绕AC、BD的交点旋转180°后,能和下面的图形重合吗?你发现了什么?平行四边形是轴对称图形吗?转一转注意观察平行四边形的对边和对角平行四边形的对边相等,对角相等。二、平行四边形性质移一移请你仔细观察结论:平行四边形的对边相等已知:四边形 ABCD是平行四边形
求证:AB=CD,BC=DA;
∠A=∠C,∠B=∠D证一证即∠BAD=∠DCB∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC∴∠3=∠4,∠1=∠2∠1=∠2
AC=CA
∠3=∠4∴ △ABC≌△CDA(ASA)∴AB=CD,BC=DA,
∠B=∠D又∵∠1=∠2,∠4=∠3∴∠1+∠4=∠2+∠3在△ABC和△CDA中证明:连接AC平行四边形的性质: 性质1:平行四边形的对边相等。平行四边形的性质对称性: 平行四边形是中心对称图形,
对角线的交点是它的对称中心。边: 平行四边形的对边平行;
平行四边形的对边相等。角: 平行四边形的对角相等;
平行四边形的邻角互补。线: 平行四边形的对角线互相平分。例1.已知:如图, ABCD中,∠A=65°,AD=6cm,求∠B,∠C,∠D的度数及BC的长度。
解:∵四边形ABCD为平行四边形(已知)
∴BC=AD (平行四边形的对边相等)
∠A=∠C,∠B=∠D (平行四边形的对角相等)
AB//CD(平行四边形的对边平行)
∵∠A=65°,AD=6cm (已知)
∴∠C=65°,BC=6cm (等量代换)
∴∠A+∠B=180° (两直线平行,同旁内角互补)
∴∠B=∠D=180°-65°=115°当堂检测: (导学案131页)1、已知 ABCD中,∠B=70°,则∠A= , ∠D= 。
2、在 ABCD中,AB=3,BC=4,则 ABCD的周长等于 。
3、在 ABCD中,已知BC=8,周长等于24,则CD= 。
4、如图, ABCD中,∠CAD=35°,∠B=40°,求∠D,∠ACD的度数110°70° 14 4解:∵ 四边形ABCD为平行四边形,
∠CAD=35°,∠B=40° (已知)
∴ ∠B=∠D =40°(平行四边形的对角相等)
∵ ∠CAD+∠D+∠ACD=180° (三角形内角和定理)
∴ ∠ACD=180° -∠CAD-∠D= 105°例2.已知:如图,在 ABCD中点E,F是对角线AC上的两点,且AE=CF.求证:BE=DF
证明:∵四边形ABCD是平行四边形(已知)
∴AB = CD
AB // CD (平行四边形的对边平行且相等)
∴∠BAE=∠DCF(两直线平行,内错角相等)
在△ABE和△CDF中
AB = CD (已证)
∠BAE=∠DCF(已证)
AE=CF (已知)
∴△BAE≌△DCF(SAS)
∴BE=DF(全等三角形对应边相等)当堂检测: (导学案132页)5、如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F。
(1)写出图中每一对你认为全等的三角形;
(2)选择(1)中的任意一对进行证明。解:(1)?△ABE≌△CDF、?△ADE≌△CBF、
?△ABD≌△CDB(2)若选:?△ABE≌△CDF
证明:∵四边形ABCD为平行四边形(已知)
∴AB=CD,AB//CD (平行四边形的对边平行且相等)
∴∠ABE=∠CDF (两直线平行,内错角相等)
∵AE⊥BD,CF⊥BD(已知)
∴∠AEB=∠CFD=90°(垂直的定义)
在△ABE和△CDF中
∠ABE=∠CDF
∵ AB=CD
∠AEB=∠CFD
∴△ABE≌△CDF(ASA)
(2)若选:?△ADE≌△CBF
证明:∵四边形ABCD为平行四边形(已知)
∴AD=BC,AD//BC (平行四边形的对边平行且相等)
∴∠ADE=∠CBF (两直线平行,内错角相等)
∵AE⊥BD,CF⊥BD(已知)
∴∠AEB=∠CFD=90°(垂直的定义)
在△ADE和△CBF中
∠ADE=∠CBF
∵ AD=BC
∠AEB=∠CFD
∴△ADE≌△CBF(ASA)
(2)若选:?△ABD≌△CDB
证明:∵四边形ABCD为平行四边形(已知)
∴AB=CD,AD=CB (平行四边形的对边相等)
在△ABE和△CDF中
AB=CD
∵ AD=CB
BD=DB
∴△ABD≌△CDB(SSS)
获? 疑?回顾与思考?作业布置:
1、课本《习题6.1》知识与技能 第1、2、3题
2、导学案 P132 《能力拓展》 谢谢大家!
1.探索交流平行四边形的有关概念和性质。
2.理解并掌握平行四边形的性质,能运用这些性
质解决简单的问题。
3.在相关的学习活动中主动探究讨论,学会与他
人合作交流。 美丽的家园,我们要好好的利用和保护她中国的骄傲,我们学习的榜样!我们的校园,学习的乐园美观别致 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?做一做1从拼图可以得到什么启示?小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题。观察拼出的这些平行四边形的对边有怎样的位置关系?为什么?1.定义:两组对边__________的四边形叫平形四边形。 一、平行四边形的相关概念分别平行几何语言:∵AB//CD,BC//AD
∴四边形ABCD是平行四边形反过来,∵四边形ABCD是平行四边形
∴AB//CD,BC//AD2、平行四边形不相邻的两个顶点连成的线段叫它的对角线。3、平行四边形相对的边称为 对边;
相对的角称为 对角;
相邻的角称为 邻角。
结论:
平行四边形是中心对称图形,对角线的交 点是它的对称中心做一做2将两个全等的平行四边形完全重叠,把上面一个平行四边形绕AC、BD的交点旋转180°后,能和下面的图形重合吗?你发现了什么?平行四边形是轴对称图形吗?转一转注意观察平行四边形的对边和对角平行四边形的对边相等,对角相等。二、平行四边形性质移一移请你仔细观察结论:平行四边形的对边相等已知:四边形 ABCD是平行四边形
求证:AB=CD,BC=DA;
∠A=∠C,∠B=∠D证一证即∠BAD=∠DCB∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC∴∠3=∠4,∠1=∠2∠1=∠2
AC=CA
∠3=∠4∴ △ABC≌△CDA(ASA)∴AB=CD,BC=DA,
∠B=∠D又∵∠1=∠2,∠4=∠3∴∠1+∠4=∠2+∠3在△ABC和△CDA中证明:连接AC平行四边形的性质: 性质1:平行四边形的对边相等。平行四边形的性质对称性: 平行四边形是中心对称图形,
对角线的交点是它的对称中心。边: 平行四边形的对边平行;
平行四边形的对边相等。角: 平行四边形的对角相等;
平行四边形的邻角互补。线: 平行四边形的对角线互相平分。例1.已知:如图, ABCD中,∠A=65°,AD=6cm,求∠B,∠C,∠D的度数及BC的长度。
解:∵四边形ABCD为平行四边形(已知)
∴BC=AD (平行四边形的对边相等)
∠A=∠C,∠B=∠D (平行四边形的对角相等)
AB//CD(平行四边形的对边平行)
∵∠A=65°,AD=6cm (已知)
∴∠C=65°,BC=6cm (等量代换)
∴∠A+∠B=180° (两直线平行,同旁内角互补)
∴∠B=∠D=180°-65°=115°当堂检测: (导学案131页)1、已知 ABCD中,∠B=70°,则∠A= , ∠D= 。
2、在 ABCD中,AB=3,BC=4,则 ABCD的周长等于 。
3、在 ABCD中,已知BC=8,周长等于24,则CD= 。
4、如图, ABCD中,∠CAD=35°,∠B=40°,求∠D,∠ACD的度数110°70° 14 4解:∵ 四边形ABCD为平行四边形,
∠CAD=35°,∠B=40° (已知)
∴ ∠B=∠D =40°(平行四边形的对角相等)
∵ ∠CAD+∠D+∠ACD=180° (三角形内角和定理)
∴ ∠ACD=180° -∠CAD-∠D= 105°例2.已知:如图,在 ABCD中点E,F是对角线AC上的两点,且AE=CF.求证:BE=DF
证明:∵四边形ABCD是平行四边形(已知)
∴AB = CD
AB // CD (平行四边形的对边平行且相等)
∴∠BAE=∠DCF(两直线平行,内错角相等)
在△ABE和△CDF中
AB = CD (已证)
∠BAE=∠DCF(已证)
AE=CF (已知)
∴△BAE≌△DCF(SAS)
∴BE=DF(全等三角形对应边相等)当堂检测: (导学案132页)5、如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F。
(1)写出图中每一对你认为全等的三角形;
(2)选择(1)中的任意一对进行证明。解:(1)?△ABE≌△CDF、?△ADE≌△CBF、
?△ABD≌△CDB(2)若选:?△ABE≌△CDF
证明:∵四边形ABCD为平行四边形(已知)
∴AB=CD,AB//CD (平行四边形的对边平行且相等)
∴∠ABE=∠CDF (两直线平行,内错角相等)
∵AE⊥BD,CF⊥BD(已知)
∴∠AEB=∠CFD=90°(垂直的定义)
在△ABE和△CDF中
∠ABE=∠CDF
∵ AB=CD
∠AEB=∠CFD
∴△ABE≌△CDF(ASA)
(2)若选:?△ADE≌△CBF
证明:∵四边形ABCD为平行四边形(已知)
∴AD=BC,AD//BC (平行四边形的对边平行且相等)
∴∠ADE=∠CBF (两直线平行,内错角相等)
∵AE⊥BD,CF⊥BD(已知)
∴∠AEB=∠CFD=90°(垂直的定义)
在△ADE和△CBF中
∠ADE=∠CBF
∵ AD=BC
∠AEB=∠CFD
∴△ADE≌△CBF(ASA)
(2)若选:?△ABD≌△CDB
证明:∵四边形ABCD为平行四边形(已知)
∴AB=CD,AD=CB (平行四边形的对边相等)
在△ABE和△CDF中
AB=CD
∵ AD=CB
BD=DB
∴△ABD≌△CDB(SSS)
获? 疑?回顾与思考?作业布置:
1、课本《习题6.1》知识与技能 第1、2、3题
2、导学案 P132 《能力拓展》 谢谢大家!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
