第12章定义命题证明(培优)(含答案)
文档属性
| 名称 | 第12章定义命题证明(培优)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 251.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第12章定义命题证明(培优)
一、单选题
1.下列运用等式的性质对等式进行的变形中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.下列计算正确的是( )
A. B. C. D.
3.下列命题是假命题的是( )
A.对顶角相等
B.两直线平行,同旁内角相等
C.同位角相等,两直线平行
D.平行于同一条直线的两直线平行
4.如图,下列推理过程及括号中所注明的推理依据错误的是( )
A.∵,∴(两直线平行,内错角相等)
B.∵,∴(内错角相等,两直线平行)
C.∵,∴(两直线平行,内错角相等)
D.∵,∴(内错角相等,两直线平行)
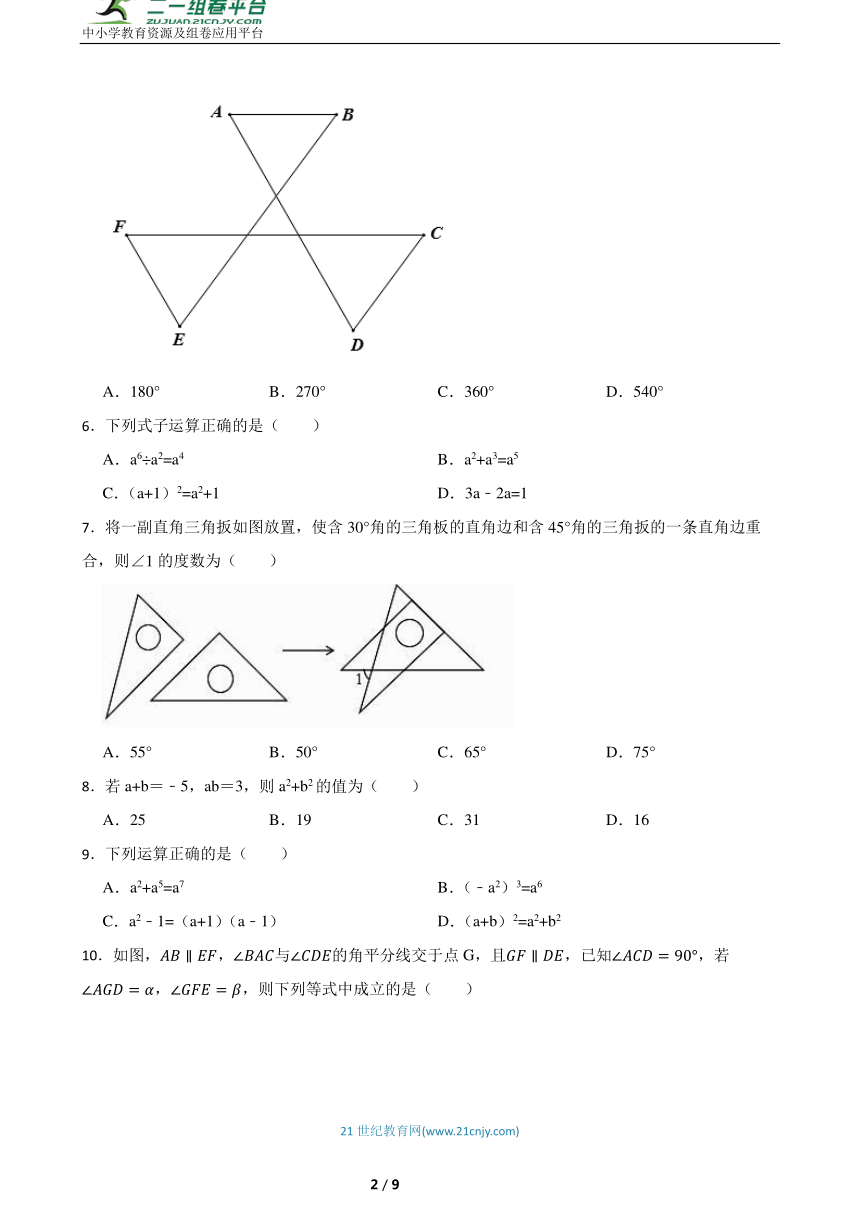
5.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180° B.270° C.360° D.540°
6.下列式子运算正确的是( )
A.a6÷a2=a4 B.a2+a3=a5
C.(a+1)2=a2+1 D.3a﹣2a=1
7.将一副直角三角扳如图放置,使含30°角的三角板的直角边和含45°角的三角扳的一条直角边重合,则∠1的度数为( )
A.55° B.50° C.65° D.75°
8.若a+b=﹣5,ab=3,则a2+b2的值为( )
A.25 B.19 C.31 D.16
9.下列运算正确的是( )
A.a2+a5=a7 B.(﹣a2)3=a6
C.a2﹣1=(a+1)(a﹣1) D.(a+b)2=a2+b2
10.如图,,与的角平分线交于点G,且,已知,若,,则下列等式中成立的是( )
A. B. C. D.
二、填空题
11.如图,已知直线a//b,,则 .
12.如图,把绕点逆时针旋转得到,若,则为 .
13.已知,,则 .
14.如图1,△ABC中,有一块直角三角板PMN放置在△ABC上(P点在△ABC内),使三角板PMN的两条直角边PM、PN恰好分别经过点B和点C.若∠A=52°,则∠1+∠2= ;
15.如图,已知,含角的直角三角板的顶点在直线上,若,则等于 .
16.在△ABC中,三个外角平分线所在的直线相交构成的三角形是 .
三、计算题
17.先化简,再求值:,其中.
18.已知:x= ,y= ﹣2,求代数式x2﹣2xy+y2的值.
19. 用乘法公式计算下列各式的值
(1)
(2)(2+1)(22+1)(24+1) (22n+1)
四、解答题
20.已知有理数m,n满足(m+n)2=9,(m-n)2=1.求下列各式的值.
(1)mn; (2)m2+n2-mn.
21.探索归纳:
(1)如图1,已知为直角三角形,,若沿图中虚线剪去,则 .
A. 90° B. 315° C. 135° D. 270°
(2)如图2,已知中,,剪去后形成四边形,则 度.
(3)如图2,根据上面的求解过程,猜想与的关系是 .
(4)如图3,若没有剪掉,而是把它折成如图3的形状,请猜想与的关系是 .
22.如图,已知 , , ,则 与 平行吗?为什么?
23.已知直线MN∥PQ,点A在直线MN上,点B、C为平面内两点,AC⊥BC于点C.
(1)如图1,当点B在直线MN上,点C在直线MN上方时,延长CB交直线PQ于点D,则∠CAB和∠CDP之间的数量关系是____.
(1)如图2,当点C在直线MN上且在点A左侧,点B在直线MN与PQ之间时,过点B作BD⊥AB交直线PQ于点D.为探究∠ABC与∠BDP之间的数量关系,小明过点B作BF∥MN.请根据他的思路,写出∠ABC与∠BDP的关系,并说明理由;
(2)如图3,在(2)的条件下,作∠ABD的平分线交直线MN于点E,当∠AEB=2∠ABC时,直接写出∠ABC的度数.
(3)如图4,当点C在直线MN上且在点A左侧,点B在直线PQ下方时,过点B作BD⊥AB交直线PQ于点D.作∠ABD的平分线交直线MN于点E,当∠BDP=2∠BEN时,请补充图形并直接写出∠ABC的度数.
答案解析部分
1.【答案】B
【知识点】等式的基本性质
2.【答案】B
【知识点】完全平方公式及运用;合并同类项法则及应用;积的乘方运算
3.【答案】B
【知识点】平行线的判定;平行线的性质;对顶角及其性质;真命题与假命题
4.【答案】B
【知识点】平行线的判定与性质
5.【答案】C
【知识点】三角形内角和定理;对顶角及其性质
6.【答案】A
【知识点】同底数幂的除法;完全平方公式及运用;合并同类项法则及应用
7.【答案】D
【知识点】三角形的外角性质
8.【答案】B
【知识点】完全平方公式及运用
9.【答案】C
【知识点】完全平方公式及运用
10.【答案】B
【知识点】平行线的判定与性质;三角形的外角性质
11.【答案】
【知识点】三角形的外角性质;同位角的概念
12.【答案】
【知识点】三角形的外角性质;旋转的性质
13.【答案】
【知识点】完全平方公式及运用
14.【答案】38°
【知识点】平行线的性质;三角形内角和定理
15.【答案】
【知识点】角的运算;三角形的外角性质;同位角的概念
16.【答案】锐角三角形
【知识点】三角形内角和定理
17.【答案】,.
【知识点】多项式乘多项式;完全平方公式及运用;平方差公式及应用;整式的混合运算
18.【答案】解:x= ,y= ﹣2, ∴x2﹣2xy+y2=(x﹣y)2=( ﹣ +2)2=22=4.
【知识点】完全平方公式及运用
19.【答案】(1)解:原式=20002-1999×(2000+1),
=20002-1999×2000-1999×1,
=2000×(2000-1999)-1999,
=2000-1999,
=1.
(2)解:原式=,
=(22-1)(22+1)(24+1)……(22n+1),
=(24-1)(24+1)……(22n+1),
=24n-1.
【知识点】有理数的乘法运算律;平方差公式及应用
20.【答案】(1)mn=2;(2)3
【知识点】完全平方公式及运用
21.【答案】(1) D
(2) 240
(3)
(4)
【知识点】三角形内角和定理;三角形的外角性质
22.【答案】解: .
理由:因为 ,所以 .
因为 , ,
所以 .
因为 , ,
所以 ,所以 .
所以 (内错角相等,两直线平行).
【知识点】平行线的判定
23.【答案】(1)解:结论:∠ABC=∠PDB.
理由:如图2中,
∵MN∥PQ,BF∥MN,
∴BF∥PQ,
∴∠PDB=∠DBF,
∵AC⊥BC,AB⊥BD,
∴∠ACB=∠ABD=90°,
∵∠CBF+∠ACB=180°,
∴∠CBF=∠ABD=90°,
∴∠ABC=∠DBF,
∴∠ABC=∠PDB.
(2)∠ABC=15°
(3)如图4中,图形如图所示,设BE交PQ于J.
∵∠BDP=2∠BEN,
∴可以假设∠BEN=x,则∠BDP=2x,
∵MN∥PQ,
∴∠BEN=∠PJE=x,
∵∠ABD=90°,BE平分∠ABD,
∴∠ABE=∠EBD=45°,
∵∠BDJ+∠BJD+∠DBJ=180°,
∴180°﹣2x+180°﹣x+45°=180°,
∴x=75°,
∵∠BCE=90°,
∴∠EBC=90°﹣75°=15°,
∴∠ABC=∠ABE﹣∠EBC=45°﹣15°=30°.
【知识点】平行线的性质;三角形内角和定理
21世纪教育网(www.21cnjy.com)
9 / 9
第12章定义命题证明(培优)
一、单选题
1.下列运用等式的性质对等式进行的变形中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.下列计算正确的是( )
A. B. C. D.
3.下列命题是假命题的是( )
A.对顶角相等
B.两直线平行,同旁内角相等
C.同位角相等,两直线平行
D.平行于同一条直线的两直线平行
4.如图,下列推理过程及括号中所注明的推理依据错误的是( )
A.∵,∴(两直线平行,内错角相等)
B.∵,∴(内错角相等,两直线平行)
C.∵,∴(两直线平行,内错角相等)
D.∵,∴(内错角相等,两直线平行)
5.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180° B.270° C.360° D.540°
6.下列式子运算正确的是( )
A.a6÷a2=a4 B.a2+a3=a5
C.(a+1)2=a2+1 D.3a﹣2a=1
7.将一副直角三角扳如图放置,使含30°角的三角板的直角边和含45°角的三角扳的一条直角边重合,则∠1的度数为( )
A.55° B.50° C.65° D.75°
8.若a+b=﹣5,ab=3,则a2+b2的值为( )
A.25 B.19 C.31 D.16
9.下列运算正确的是( )
A.a2+a5=a7 B.(﹣a2)3=a6
C.a2﹣1=(a+1)(a﹣1) D.(a+b)2=a2+b2
10.如图,,与的角平分线交于点G,且,已知,若,,则下列等式中成立的是( )
A. B. C. D.
二、填空题
11.如图,已知直线a//b,,则 .
12.如图,把绕点逆时针旋转得到,若,则为 .
13.已知,,则 .
14.如图1,△ABC中,有一块直角三角板PMN放置在△ABC上(P点在△ABC内),使三角板PMN的两条直角边PM、PN恰好分别经过点B和点C.若∠A=52°,则∠1+∠2= ;
15.如图,已知,含角的直角三角板的顶点在直线上,若,则等于 .
16.在△ABC中,三个外角平分线所在的直线相交构成的三角形是 .
三、计算题
17.先化简,再求值:,其中.
18.已知:x= ,y= ﹣2,求代数式x2﹣2xy+y2的值.
19. 用乘法公式计算下列各式的值
(1)
(2)(2+1)(22+1)(24+1) (22n+1)
四、解答题
20.已知有理数m,n满足(m+n)2=9,(m-n)2=1.求下列各式的值.
(1)mn; (2)m2+n2-mn.
21.探索归纳:
(1)如图1,已知为直角三角形,,若沿图中虚线剪去,则 .
A. 90° B. 315° C. 135° D. 270°
(2)如图2,已知中,,剪去后形成四边形,则 度.
(3)如图2,根据上面的求解过程,猜想与的关系是 .
(4)如图3,若没有剪掉,而是把它折成如图3的形状,请猜想与的关系是 .
22.如图,已知 , , ,则 与 平行吗?为什么?
23.已知直线MN∥PQ,点A在直线MN上,点B、C为平面内两点,AC⊥BC于点C.
(1)如图1,当点B在直线MN上,点C在直线MN上方时,延长CB交直线PQ于点D,则∠CAB和∠CDP之间的数量关系是____.
(1)如图2,当点C在直线MN上且在点A左侧,点B在直线MN与PQ之间时,过点B作BD⊥AB交直线PQ于点D.为探究∠ABC与∠BDP之间的数量关系,小明过点B作BF∥MN.请根据他的思路,写出∠ABC与∠BDP的关系,并说明理由;
(2)如图3,在(2)的条件下,作∠ABD的平分线交直线MN于点E,当∠AEB=2∠ABC时,直接写出∠ABC的度数.
(3)如图4,当点C在直线MN上且在点A左侧,点B在直线PQ下方时,过点B作BD⊥AB交直线PQ于点D.作∠ABD的平分线交直线MN于点E,当∠BDP=2∠BEN时,请补充图形并直接写出∠ABC的度数.
答案解析部分
1.【答案】B
【知识点】等式的基本性质
2.【答案】B
【知识点】完全平方公式及运用;合并同类项法则及应用;积的乘方运算
3.【答案】B
【知识点】平行线的判定;平行线的性质;对顶角及其性质;真命题与假命题
4.【答案】B
【知识点】平行线的判定与性质
5.【答案】C
【知识点】三角形内角和定理;对顶角及其性质
6.【答案】A
【知识点】同底数幂的除法;完全平方公式及运用;合并同类项法则及应用
7.【答案】D
【知识点】三角形的外角性质
8.【答案】B
【知识点】完全平方公式及运用
9.【答案】C
【知识点】完全平方公式及运用
10.【答案】B
【知识点】平行线的判定与性质;三角形的外角性质
11.【答案】
【知识点】三角形的外角性质;同位角的概念
12.【答案】
【知识点】三角形的外角性质;旋转的性质
13.【答案】
【知识点】完全平方公式及运用
14.【答案】38°
【知识点】平行线的性质;三角形内角和定理
15.【答案】
【知识点】角的运算;三角形的外角性质;同位角的概念
16.【答案】锐角三角形
【知识点】三角形内角和定理
17.【答案】,.
【知识点】多项式乘多项式;完全平方公式及运用;平方差公式及应用;整式的混合运算
18.【答案】解:x= ,y= ﹣2, ∴x2﹣2xy+y2=(x﹣y)2=( ﹣ +2)2=22=4.
【知识点】完全平方公式及运用
19.【答案】(1)解:原式=20002-1999×(2000+1),
=20002-1999×2000-1999×1,
=2000×(2000-1999)-1999,
=2000-1999,
=1.
(2)解:原式=,
=(22-1)(22+1)(24+1)……(22n+1),
=(24-1)(24+1)……(22n+1),
=24n-1.
【知识点】有理数的乘法运算律;平方差公式及应用
20.【答案】(1)mn=2;(2)3
【知识点】完全平方公式及运用
21.【答案】(1) D
(2) 240
(3)
(4)
【知识点】三角形内角和定理;三角形的外角性质
22.【答案】解: .
理由:因为 ,所以 .
因为 , ,
所以 .
因为 , ,
所以 ,所以 .
所以 (内错角相等,两直线平行).
【知识点】平行线的判定
23.【答案】(1)解:结论:∠ABC=∠PDB.
理由:如图2中,
∵MN∥PQ,BF∥MN,
∴BF∥PQ,
∴∠PDB=∠DBF,
∵AC⊥BC,AB⊥BD,
∴∠ACB=∠ABD=90°,
∵∠CBF+∠ACB=180°,
∴∠CBF=∠ABD=90°,
∴∠ABC=∠DBF,
∴∠ABC=∠PDB.
(2)∠ABC=15°
(3)如图4中,图形如图所示,设BE交PQ于J.
∵∠BDP=2∠BEN,
∴可以假设∠BEN=x,则∠BDP=2x,
∵MN∥PQ,
∴∠BEN=∠PJE=x,
∵∠ABD=90°,BE平分∠ABD,
∴∠ABE=∠EBD=45°,
∵∠BDJ+∠BJD+∠DBJ=180°,
∴180°﹣2x+180°﹣x+45°=180°,
∴x=75°,
∵∠BCE=90°,
∴∠EBC=90°﹣75°=15°,
∴∠ABC=∠ABE﹣∠EBC=45°﹣15°=30°.
【知识点】平行线的性质;三角形内角和定理
21世纪教育网(www.21cnjy.com)
9 / 9
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
