圆周角和圆心角的关系课件(共21张PPT)
文档属性
| 名称 | 圆周角和圆心角的关系课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 209.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-20 23:43:39 | ||
图片预览




文档简介
课件21张PPT。九年级数学(下)第三章圆3.3 圆周角和圆心角
的关系(3)
——圆周角定理推论知识点回顾同弧或等弧所对的圆周角____一、圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的______.圆周角定理推论1:圆周角定理推论2:圆的内接四边形对角______一半相等互补1.如图,在⊙O中,∠BAC=32o,则∠BOC=________。
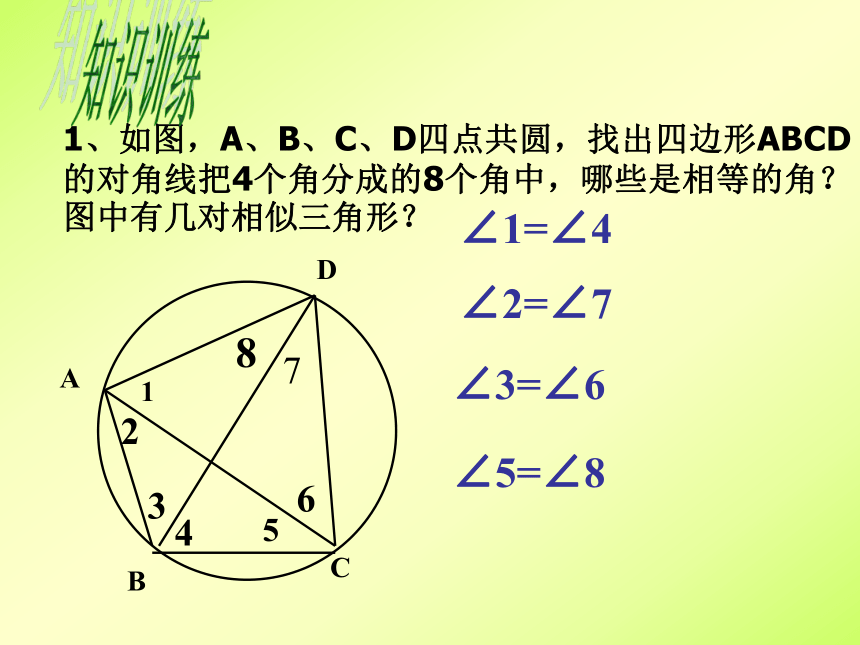
2、如图,⊙O中,∠ACB = 130o,则∠AOB=______。64o100o知识训练B1、如图,A、B、C、D四点共圆,找出四边形ABCD的对角线把4个角分成的8个角中,哪些是相等的角?图中有几对相似三角形?∠2=∠7∠1=∠4∠3=∠6∠5=∠8知识训练做一做 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁,如图,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点, ∠ACB就是”危险角”,(1)当船P位于安全区域时,它与两灯塔的
夹角∠a与“危险角”有怎样的大小关系?(2)当船P位于危险区域时,
它与两灯塔的夹角∠a
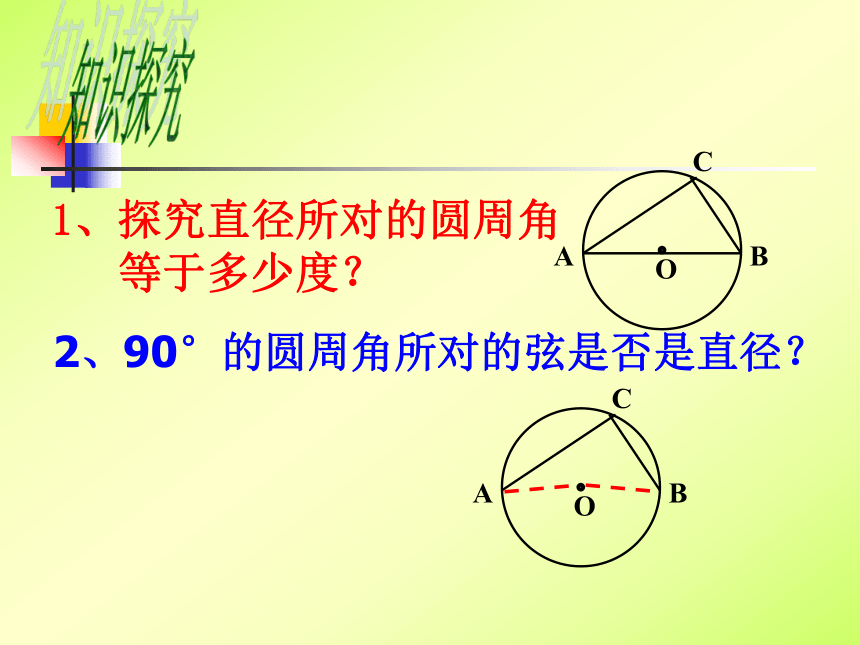
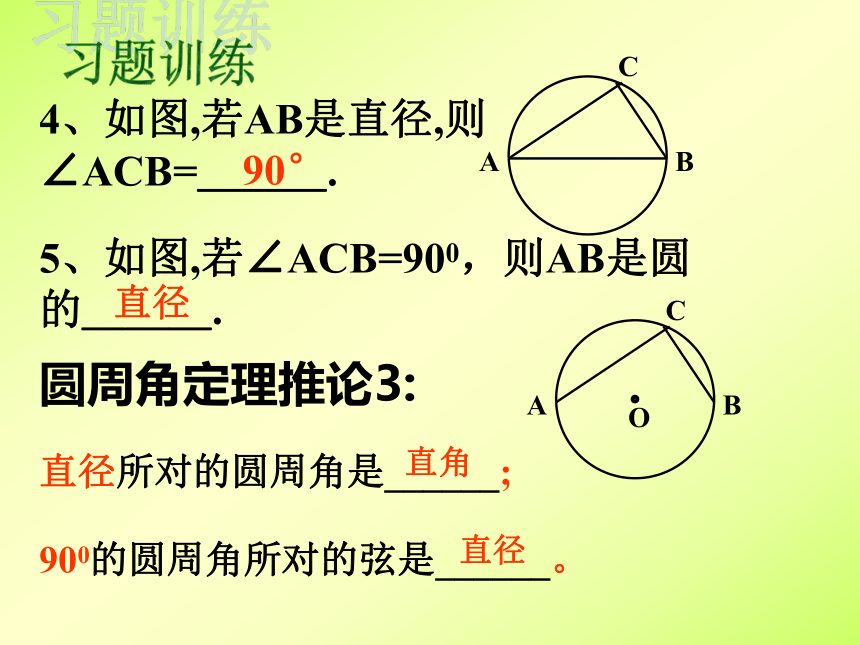
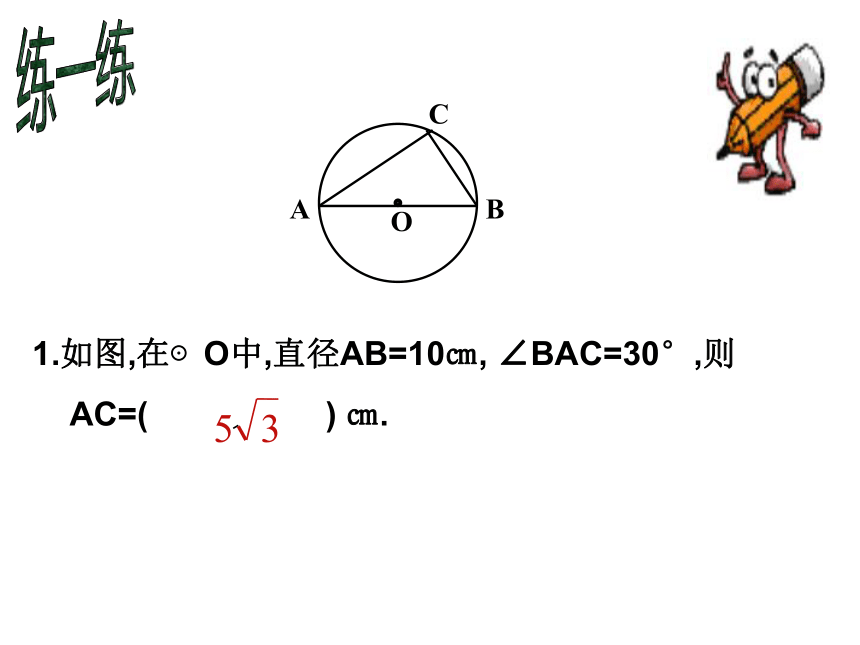
与“危险角”有怎样的大小关系?1、探究直径所对的圆周角 等于多少度? 知识探究2、90°的圆周角所对的弦是否是直径?ABC4、如图,若AB是直径,则∠ACB=___.90°直径所对的圆周角是______;900的圆周角所对的弦是______。圆周角定理推论3:习题训练5、如图,若∠ACB=900,则AB是圆的___.直径直角直径练一练1.如图,在⊙O中,直径AB=10㎝, ∠BAC=30°,则
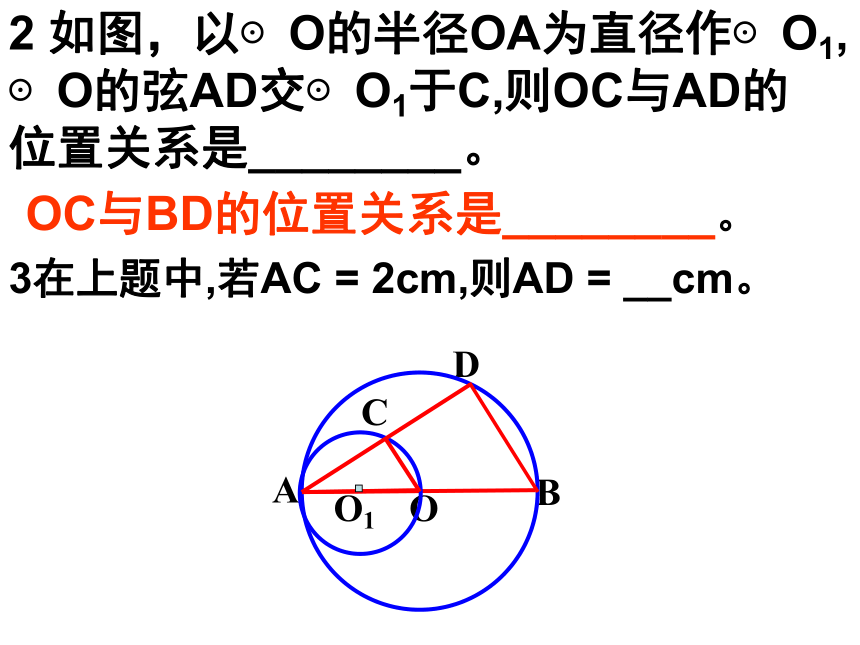
AC=( ) ㎝.2 如图,以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则OC与AD的
位置关系是________。3在上题中,若AC = 2cm,则AD = __cm。OC与BD的位置关系是________。1.如图,AB是⊙O的直径,BD是弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?典型例题解:BD=CD.理由是:连接AD.∵AB是⊙O的直径∴∠ADB=90°即AD⊥BD又∵AC=AB∴BD=CD圆的辅助线作法二:见直径,连圆周角2.如图,AB是⊙O的直径,∠C=15°
求∠BAD的度数.
3.如图,AB是⊙O的直径,弦
CD与AB相交于点E,
∠ACD=60°,∠ADC=50°
求∠CEB的度数.
4.如图,△ABC的3个顶点都在⊙O上,直径AD=4,∠ABC=∠DAC,求AC的长5、如图,在⊙O中,直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D。求BC和AD的长6.如图,在半径为5的⊙O中,
弦AB=6,点C是优弧AB上
一点(不与A、B重合),则
cosC的值为_______.7.如图,圆O是△ABC的外接圆,若圆O的半径为1.5,AC=2 ,则SinB的值是( )8.如图,△ABC内接于⊙O,
∠C=45°,AB=2,则
⊙O的半径为( )
A.1 B. C.2 D.推论1:
圆内接四边形对角_______。
圆周角定理:
圆周角的度数等于_________________总结:推论3: 直径所对的圆周角是_______;
90度的圆周角所对的弦是______。推论2:
同弧或等弧所对的圆周角______;互补相等直角直径利用三角尺可以画出圆的直径,为什么?你能用
这种方法确定一个圆形工件的圆心吗?习题训练证明:连结AD.∵AB是圆的直径∴∠ADB=90°,∴AD⊥BC∵AB=AC,∴AD平分∠BAC,即∠1=∠2,(同圆或等圆中,相等的圆周角所对弧相等)。巩固训练拓展提升3. 如图,AD是△ABC的高,AE是△ABC的外接圆直径。
求证:AB · AC = AE · ADAOBCDE∵AE是△ABC的外接圆直径∴△ADC∽ △ABE∴∠ABE=90°∵AD是△ABC的高∴∠ADC=∠ABE=90°∵∠C=∠E( )∴∴ AB · AC = AE · AD 证明:连接BE.1、证明题的思路寻找方法;
2、等积式的证明方法;
3、辅助线的思考方法。
的关系(3)
——圆周角定理推论知识点回顾同弧或等弧所对的圆周角____一、圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的______.圆周角定理推论1:圆周角定理推论2:圆的内接四边形对角______一半相等互补1.如图,在⊙O中,∠BAC=32o,则∠BOC=________。
2、如图,⊙O中,∠ACB = 130o,则∠AOB=______。64o100o知识训练B1、如图,A、B、C、D四点共圆,找出四边形ABCD的对角线把4个角分成的8个角中,哪些是相等的角?图中有几对相似三角形?∠2=∠7∠1=∠4∠3=∠6∠5=∠8知识训练做一做 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁,如图,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点, ∠ACB就是”危险角”,(1)当船P位于安全区域时,它与两灯塔的
夹角∠a与“危险角”有怎样的大小关系?(2)当船P位于危险区域时,
它与两灯塔的夹角∠a
与“危险角”有怎样的大小关系?1、探究直径所对的圆周角 等于多少度? 知识探究2、90°的圆周角所对的弦是否是直径?ABC4、如图,若AB是直径,则∠ACB=___.90°直径所对的圆周角是______;900的圆周角所对的弦是______。圆周角定理推论3:习题训练5、如图,若∠ACB=900,则AB是圆的___.直径直角直径练一练1.如图,在⊙O中,直径AB=10㎝, ∠BAC=30°,则
AC=( ) ㎝.2 如图,以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则OC与AD的
位置关系是________。3在上题中,若AC = 2cm,则AD = __cm。OC与BD的位置关系是________。1.如图,AB是⊙O的直径,BD是弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?典型例题解:BD=CD.理由是:连接AD.∵AB是⊙O的直径∴∠ADB=90°即AD⊥BD又∵AC=AB∴BD=CD圆的辅助线作法二:见直径,连圆周角2.如图,AB是⊙O的直径,∠C=15°
求∠BAD的度数.
3.如图,AB是⊙O的直径,弦
CD与AB相交于点E,
∠ACD=60°,∠ADC=50°
求∠CEB的度数.
4.如图,△ABC的3个顶点都在⊙O上,直径AD=4,∠ABC=∠DAC,求AC的长5、如图,在⊙O中,直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D。求BC和AD的长6.如图,在半径为5的⊙O中,
弦AB=6,点C是优弧AB上
一点(不与A、B重合),则
cosC的值为_______.7.如图,圆O是△ABC的外接圆,若圆O的半径为1.5,AC=2 ,则SinB的值是( )8.如图,△ABC内接于⊙O,
∠C=45°,AB=2,则
⊙O的半径为( )
A.1 B. C.2 D.推论1:
圆内接四边形对角_______。
圆周角定理:
圆周角的度数等于_________________总结:推论3: 直径所对的圆周角是_______;
90度的圆周角所对的弦是______。推论2:
同弧或等弧所对的圆周角______;互补相等直角直径利用三角尺可以画出圆的直径,为什么?你能用
这种方法确定一个圆形工件的圆心吗?习题训练证明:连结AD.∵AB是圆的直径∴∠ADB=90°,∴AD⊥BC∵AB=AC,∴AD平分∠BAC,即∠1=∠2,(同圆或等圆中,相等的圆周角所对弧相等)。巩固训练拓展提升3. 如图,AD是△ABC的高,AE是△ABC的外接圆直径。
求证:AB · AC = AE · ADAOBCDE∵AE是△ABC的外接圆直径∴△ADC∽ △ABE∴∠ABE=90°∵AD是△ABC的高∴∠ADC=∠ABE=90°∵∠C=∠E( )∴∴ AB · AC = AE · AD 证明:连接BE.1、证明题的思路寻找方法;
2、等积式的证明方法;
3、辅助线的思考方法。
