北师大版九年级下册第三章3.1圆的课件(共45张PPT)
文档属性
| 名称 | 北师大版九年级下册第三章3.1圆的课件(共45张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-20 23:40:52 | ||
图片预览





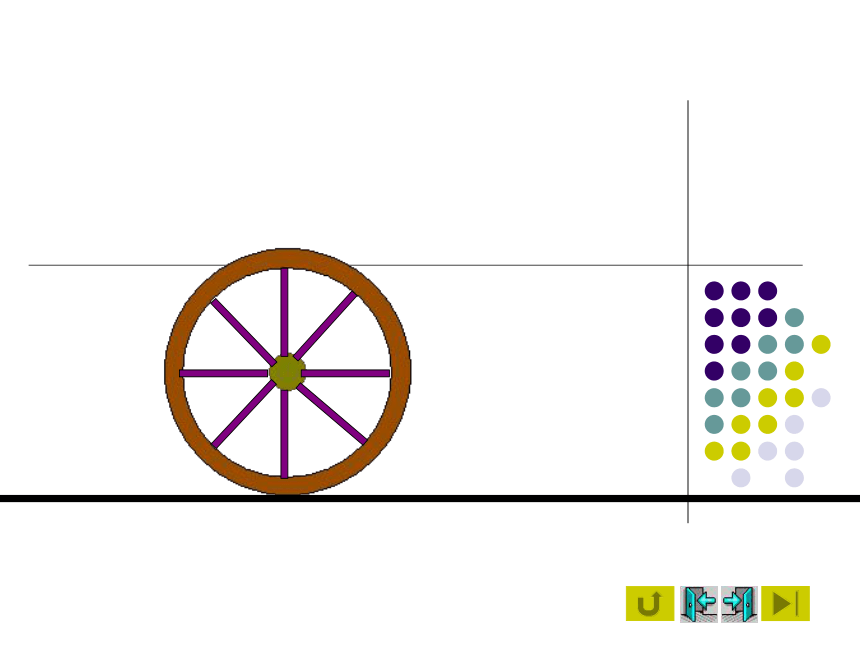

文档简介
(共44张PPT)
圆
观察车轮,
你发现了什么?
车轮为什么做成圆形
二、探 求 新 知
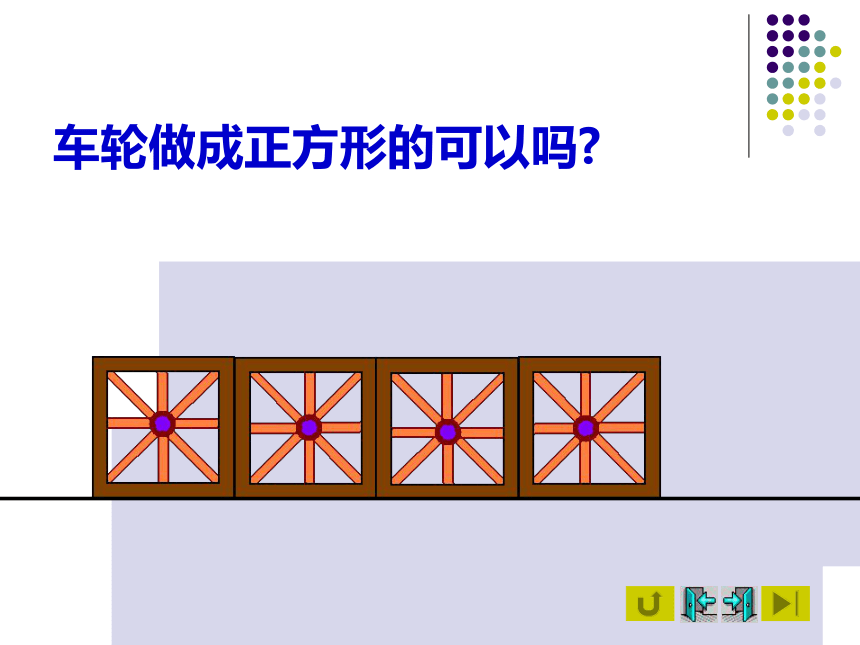
车轮做成三角形、正方形可以吗?
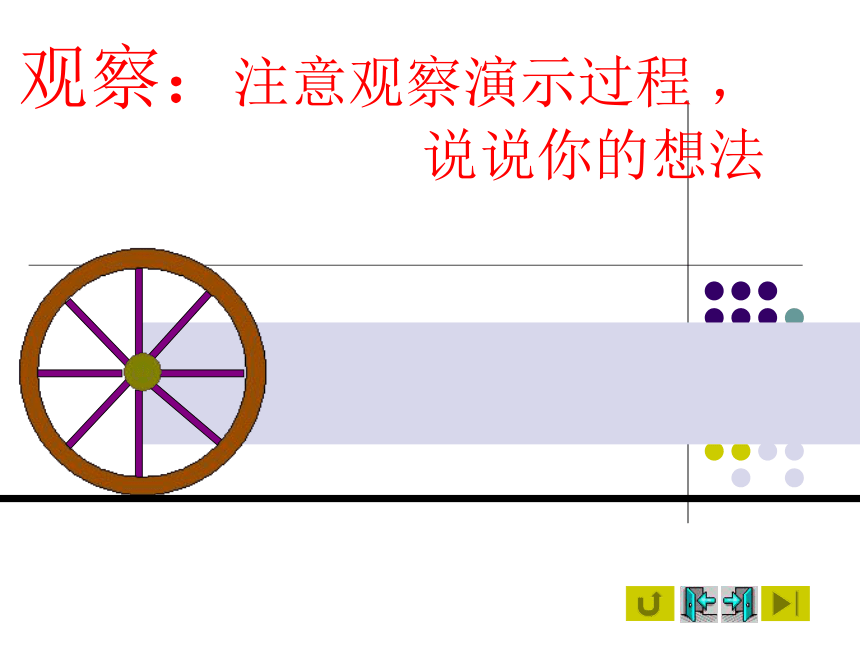
骑车运动
看了此画,你有何想法
观察:注意观察演示过程 ,说说你的想法
车轮做成正方形的可以吗
A .
. B
. C
A .
. B
. C
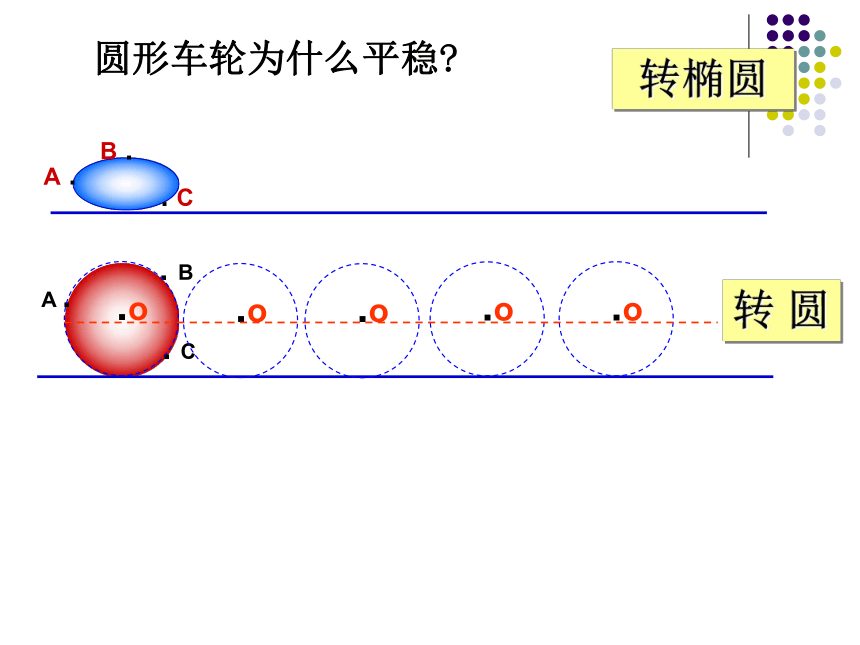
转 圆
A .
B .
. C
A .
B .
. C
转椭圆
.o
.o
.o
.o
.o
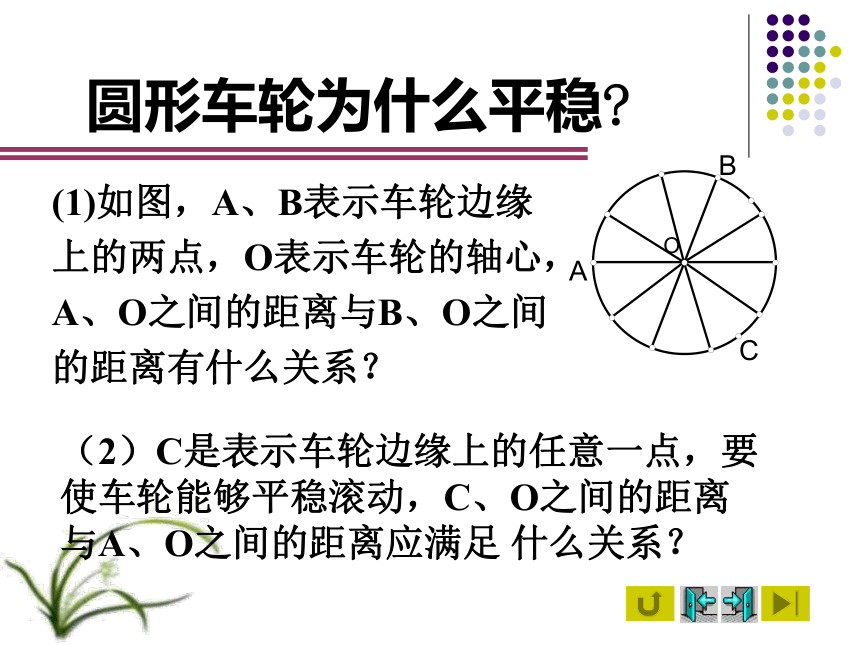
圆形车轮为什么平稳
圆形车轮为什么平稳
(2)C是表示车轮边缘上的任意一点,要使车轮能够平稳滚动,C、O之间的距离与A、O之间的距离应满足 什么关系?
(1)如图,A、B表示车轮边缘
上的两点,O表示车轮的轴心,
A、O之间的距离与B、O之间
的距离有什么关系?
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感到非常平稳,这就是车轮都做成圆形的数学道理。
三、投圈游戏
(1) 体育老师规定以 3 米为距离, 4 个人一组进行比赛,这样的队形公平吗
投圈游戏
(2)体育老师规定以 3 米为距离, 4 个人一组
进行比赛.
A
B
D
C
.
O
.
A
B
C
D
O
O
.
请你确定他们的位置.
投圈游戏
(2) 体育老师规定以 3 米为距离, 一组进行比赛, 如何确定他们的位置
20个人
4个人
10个人
n 个人
投圈游戏
A
B
D
C
.
O
.
A
B
C
D
O
O
.
投圈游戏
(3) 你能帮老师在操场上把这个圆画出来吗
投圈游戏
(3) 你能帮老师在操场上把这个圆画出来吗
将绳子的一端 A 固定,然后拉紧绳子的另一端B (AB=3米) , 并绕A在地面上转一周,点 B 所经过的路径就是所要作的圆
演 示
A
B
投圈游戏
(4) 同学们站在圆上的任意位置,游戏都公平吗
.
被投物体
3米
圆上每一个点到定点 的距离都等于定长 !
定点(圆心)
(5) 除了这个圆周,还有其它位置到被投物体的距离
为 3 米吗
到定点的距离等于定长的所有点都在这个圆上!
定长(半径)
(圆心)
(半径)
四、学习新知
知识点一、圆的定义:
定点叫做圆心,定长叫做半径。
2 、 从圆的定义可知:圆是指_____而不是______。
注意:1、确定圆的要素是:______________。
圆心确定圆的______,半径确定圆的______,确定一个圆,两者缺一不可。
以点O为圆心的圆记作:
“⊙O”,读作:“圆O”。
圆周
圆面
圆心和半径
平面上到定点的距离等于定长的所有点组成的图形叫做圆
位置
大小
想一想
A
B
F
G
H
I
J
K
D
E
C
如图是圆形靶的示意图
点A、B所在的位置有什么共同特点?
点C、D、E呢?
F、G、H、I、J、K呢?
综上可得:
知识点二、 点和圆有____种位置关系:
_____________
_____________
_____________
点在圆内
点在圆上
点在圆外
三
O
r
B
C
A
已知及⊙O其平面内的点A、B、C,⊙O的半径为r,则
点A在⊙O______ OA_____r
点B在⊙O______ OB_____r
点C在⊙O______ OC_____r
上
=
外
>
内
<
新知识总结
设⊙O的半径为r,点P与圆心O的距离为d,则有:
d___r
(1)点P在⊙O上
(2)点P在⊙O内
(3)点P在⊙O外
反之,也成立:
点P在⊙O上
点P在⊙O内
点P在⊙O外
O
P
P
P
d___r
d___r
d___r
(1)点P在⊙O上
d___r
(1)点P在⊙O上
(2)点P在⊙O内
d___r
(3)点P在⊙O外
d___r
(3)点P在⊙O外
d___r
=
<
>
(3) d>r
(1) d=r
(2) d<r
r
d
d
d
例1:已知⊙O的半径r=2cm,
(1)当OP 时,点P在⊙O上;
(2)当OA=1cm时,点A在 ;
(3)当OB=4cm时,点B在 。
=2cm
⊙O内
⊙O外
例2 已知:如图,矩形ABCD的对角线相交于点O,
(1)试猜想:矩形的四个顶点在同一个圆上吗?
(2)如果在同一个圆上,是在怎样一个圆上,并给予证明?如果不在同一个圆上,试说明为什么?
(3)若E、F、G、H分别是OA、OB、OC、OD的中点,E、F、G、H是在同一个圆上吗?
五、学以致用
课堂练习:
上
内
外
上
点A在⊙O内部
点A在⊙O上
点A在⊙O外部
1、正方形ABCD的边长为3cm,以A为圆心,3cm长为半径作⊙A,则点A在⊙A ,点B在⊙A ,点C在⊙A ,点D在⊙A 。
当OP=10cm时, ;
当OP=14cm时, 。
2.已知点A为线段OP的中点, ⊙O的半径是5 cm,当OP满足下列条件时,分别指出点A与⊙O的位置关系:
当OP= 6cm时, ;
3、已知⊙ P的半径为3,点Q在⊙ P外,点R在⊙ P上,点H在⊙ P内,则PQ___3,PR____3,PH_____3.
课堂练习:
4、如图,Rt△ABC的两条直角边BC=3cm,AC=4cm,斜边AB上的高为CD.若以C为圆心,分别以r1=2cm,r2=2.4cm,r3=3cm为半径作圆,试判断D点与这三个圆的位置关系.
D
A
B
C
O
1
5. 边长为1的正方形ABCD的对角线交于O点,以A为圆心,以1为半径画圆,则B,C,D,O各点与⊙A的关系是什么?
6.在直角△ABC中,∠C为直角,AC=8,
AB=10,AB的中点为D,以C点为圆心
C
A
B
D
8
10
(1)若以5为半径画
⊙C,则点A,B,D与
⊙C的关系是什么?
6.在直角△ABC中,∠C为直角,AC=8,
AB=10,AB的中点为D,以C点为圆心
C
A
B
D
8
10
(2)若以6为半径画
⊙C,则点A,B,D与
⊙C的关系是什么?
(3)若A,B,D三点
一个在圆内,且
至少一个在圆外,
则⊙C的半径r的取值范围。
7.已知:如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别为OA、OB的中点.求证:MC=NC.
8.如图:以△OAB的顶点O为圆心的圆与AB边交于C,D点,且AC=DB.
求证: △OAB为等腰三角形。
1.已知点P为平面上一点,且P到⊙O上的点的最大距离是5,最小距离是3,求⊙O的半径。
问题探求:
(1)和点A、B的距离都等于2厘米的点的集合;
2.设AB=3厘米,画图并说明具有下列性质的点的集合是怎样的图形:
(分别以点A、B为圆心,2厘米长为半径的⊙A和⊙ B的交点)
B
A
问题探求:
2.设AB=3厘米,画图并说明具有下列性质的点的集合是怎样的图形:
(2)和点A、B的距离都小于2厘米的点的集合.
(分别以点A、B为圆心,2厘米长为半径的⊙A的内部与⊙ B的内部的公共部分)
A
B
3.用一用(课本P94页第1题)
在“用一用”中,如果绳子的长度放长到7米,请画出羊的活动区域,并计算活动区域的面积.
7
如图,一根3m长的绳子,一端栓在柱子上,
另一端栓
着一只羊,
请画出羊
的活动区域.
4.用一用
6
如果绳子的长度
放长到6米?
5m
o
4m
5m
o
4m
正确答案
课堂小结:
定义一: 在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆。 固定的端点O叫做圆心,线段OA叫做半径。
1、从运动和集合的观点理解圆的定义:
定义二:圆是到定点的距离等于定长的点的集合。
3、证明几个点在同一个圆上的方法。
要证明几个点在同一个圆上,只要证明这几个点到一个该圆心的距离相等。
2、点与圆的位置关系:
设⊙O的半径为r,则点P与⊙O的位置关系有:
(1)点P在⊙O上 OP=r
(2)点P在⊙O内 OP<r
(3)点P在⊙O外 OP>r
1.下列图形中,四个顶点在同一个圆上的是( )
A.矩形、平行四边形 B.正方形、菱形
C .正方形、平行四边形 D.矩形、等腰梯形
能力提升
2、如图,已知矩形ABCD
的边AB=3厘米,AD=4厘米。
(1)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(2)若以A点为圆心作圆A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则圆A的半径r的取值范围是什么?
能力提升
3. 一个8×10米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,你准备安装几个 怎样安装 请说明理由.
圆
观察车轮,
你发现了什么?
车轮为什么做成圆形
二、探 求 新 知
车轮做成三角形、正方形可以吗?
骑车运动
看了此画,你有何想法
观察:注意观察演示过程 ,说说你的想法
车轮做成正方形的可以吗
A .
. B
. C
A .
. B
. C
转 圆
A .
B .
. C
A .
B .
. C
转椭圆
.o
.o
.o
.o
.o
圆形车轮为什么平稳
圆形车轮为什么平稳
(2)C是表示车轮边缘上的任意一点,要使车轮能够平稳滚动,C、O之间的距离与A、O之间的距离应满足 什么关系?
(1)如图,A、B表示车轮边缘
上的两点,O表示车轮的轴心,
A、O之间的距离与B、O之间
的距离有什么关系?
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感到非常平稳,这就是车轮都做成圆形的数学道理。
三、投圈游戏
(1) 体育老师规定以 3 米为距离, 4 个人一组进行比赛,这样的队形公平吗
投圈游戏
(2)体育老师规定以 3 米为距离, 4 个人一组
进行比赛.
A
B
D
C
.
O
.
A
B
C
D
O
O
.
请你确定他们的位置.
投圈游戏
(2) 体育老师规定以 3 米为距离, 一组进行比赛, 如何确定他们的位置
20个人
4个人
10个人
n 个人
投圈游戏
A
B
D
C
.
O
.
A
B
C
D
O
O
.
投圈游戏
(3) 你能帮老师在操场上把这个圆画出来吗
投圈游戏
(3) 你能帮老师在操场上把这个圆画出来吗
将绳子的一端 A 固定,然后拉紧绳子的另一端B (AB=3米) , 并绕A在地面上转一周,点 B 所经过的路径就是所要作的圆
演 示
A
B
投圈游戏
(4) 同学们站在圆上的任意位置,游戏都公平吗
.
被投物体
3米
圆上每一个点到定点 的距离都等于定长 !
定点(圆心)
(5) 除了这个圆周,还有其它位置到被投物体的距离
为 3 米吗
到定点的距离等于定长的所有点都在这个圆上!
定长(半径)
(圆心)
(半径)
四、学习新知
知识点一、圆的定义:
定点叫做圆心,定长叫做半径。
2 、 从圆的定义可知:圆是指_____而不是______。
注意:1、确定圆的要素是:______________。
圆心确定圆的______,半径确定圆的______,确定一个圆,两者缺一不可。
以点O为圆心的圆记作:
“⊙O”,读作:“圆O”。
圆周
圆面
圆心和半径
平面上到定点的距离等于定长的所有点组成的图形叫做圆
位置
大小
想一想
A
B
F
G
H
I
J
K
D
E
C
如图是圆形靶的示意图
点A、B所在的位置有什么共同特点?
点C、D、E呢?
F、G、H、I、J、K呢?
综上可得:
知识点二、 点和圆有____种位置关系:
_____________
_____________
_____________
点在圆内
点在圆上
点在圆外
三
O
r
B
C
A
已知及⊙O其平面内的点A、B、C,⊙O的半径为r,则
点A在⊙O______ OA_____r
点B在⊙O______ OB_____r
点C在⊙O______ OC_____r
上
=
外
>
内
<
新知识总结
设⊙O的半径为r,点P与圆心O的距离为d,则有:
d___r
(1)点P在⊙O上
(2)点P在⊙O内
(3)点P在⊙O外
反之,也成立:
点P在⊙O上
点P在⊙O内
点P在⊙O外
O
P
P
P
d___r
d___r
d___r
(1)点P在⊙O上
d___r
(1)点P在⊙O上
(2)点P在⊙O内
d___r
(3)点P在⊙O外
d___r
(3)点P在⊙O外
d___r
=
<
>
(3) d>r
(1) d=r
(2) d<r
r
d
d
d
例1:已知⊙O的半径r=2cm,
(1)当OP 时,点P在⊙O上;
(2)当OA=1cm时,点A在 ;
(3)当OB=4cm时,点B在 。
=2cm
⊙O内
⊙O外
例2 已知:如图,矩形ABCD的对角线相交于点O,
(1)试猜想:矩形的四个顶点在同一个圆上吗?
(2)如果在同一个圆上,是在怎样一个圆上,并给予证明?如果不在同一个圆上,试说明为什么?
(3)若E、F、G、H分别是OA、OB、OC、OD的中点,E、F、G、H是在同一个圆上吗?
五、学以致用
课堂练习:
上
内
外
上
点A在⊙O内部
点A在⊙O上
点A在⊙O外部
1、正方形ABCD的边长为3cm,以A为圆心,3cm长为半径作⊙A,则点A在⊙A ,点B在⊙A ,点C在⊙A ,点D在⊙A 。
当OP=10cm时, ;
当OP=14cm时, 。
2.已知点A为线段OP的中点, ⊙O的半径是5 cm,当OP满足下列条件时,分别指出点A与⊙O的位置关系:
当OP= 6cm时, ;
3、已知⊙ P的半径为3,点Q在⊙ P外,点R在⊙ P上,点H在⊙ P内,则PQ___3,PR____3,PH_____3.
课堂练习:
4、如图,Rt△ABC的两条直角边BC=3cm,AC=4cm,斜边AB上的高为CD.若以C为圆心,分别以r1=2cm,r2=2.4cm,r3=3cm为半径作圆,试判断D点与这三个圆的位置关系.
D
A
B
C
O
1
5. 边长为1的正方形ABCD的对角线交于O点,以A为圆心,以1为半径画圆,则B,C,D,O各点与⊙A的关系是什么?
6.在直角△ABC中,∠C为直角,AC=8,
AB=10,AB的中点为D,以C点为圆心
C
A
B
D
8
10
(1)若以5为半径画
⊙C,则点A,B,D与
⊙C的关系是什么?
6.在直角△ABC中,∠C为直角,AC=8,
AB=10,AB的中点为D,以C点为圆心
C
A
B
D
8
10
(2)若以6为半径画
⊙C,则点A,B,D与
⊙C的关系是什么?
(3)若A,B,D三点
一个在圆内,且
至少一个在圆外,
则⊙C的半径r的取值范围。
7.已知:如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别为OA、OB的中点.求证:MC=NC.
8.如图:以△OAB的顶点O为圆心的圆与AB边交于C,D点,且AC=DB.
求证: △OAB为等腰三角形。
1.已知点P为平面上一点,且P到⊙O上的点的最大距离是5,最小距离是3,求⊙O的半径。
问题探求:
(1)和点A、B的距离都等于2厘米的点的集合;
2.设AB=3厘米,画图并说明具有下列性质的点的集合是怎样的图形:
(分别以点A、B为圆心,2厘米长为半径的⊙A和⊙ B的交点)
B
A
问题探求:
2.设AB=3厘米,画图并说明具有下列性质的点的集合是怎样的图形:
(2)和点A、B的距离都小于2厘米的点的集合.
(分别以点A、B为圆心,2厘米长为半径的⊙A的内部与⊙ B的内部的公共部分)
A
B
3.用一用(课本P94页第1题)
在“用一用”中,如果绳子的长度放长到7米,请画出羊的活动区域,并计算活动区域的面积.
7
如图,一根3m长的绳子,一端栓在柱子上,
另一端栓
着一只羊,
请画出羊
的活动区域.
4.用一用
6
如果绳子的长度
放长到6米?
5m
o
4m
5m
o
4m
正确答案
课堂小结:
定义一: 在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆。 固定的端点O叫做圆心,线段OA叫做半径。
1、从运动和集合的观点理解圆的定义:
定义二:圆是到定点的距离等于定长的点的集合。
3、证明几个点在同一个圆上的方法。
要证明几个点在同一个圆上,只要证明这几个点到一个该圆心的距离相等。
2、点与圆的位置关系:
设⊙O的半径为r,则点P与⊙O的位置关系有:
(1)点P在⊙O上 OP=r
(2)点P在⊙O内 OP<r
(3)点P在⊙O外 OP>r
1.下列图形中,四个顶点在同一个圆上的是( )
A.矩形、平行四边形 B.正方形、菱形
C .正方形、平行四边形 D.矩形、等腰梯形
能力提升
2、如图,已知矩形ABCD
的边AB=3厘米,AD=4厘米。
(1)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(2)若以A点为圆心作圆A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则圆A的半径r的取值范围是什么?
能力提升
3. 一个8×10米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,你准备安装几个 怎样安装 请说明理由.
