北师大版九年级下册第三章3.6 直线与圆的位置关系课件
文档属性
| 名称 | 北师大版九年级下册第三章3.6 直线与圆的位置关系课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 217.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-20 00:00:00 | ||
图片预览





文档简介
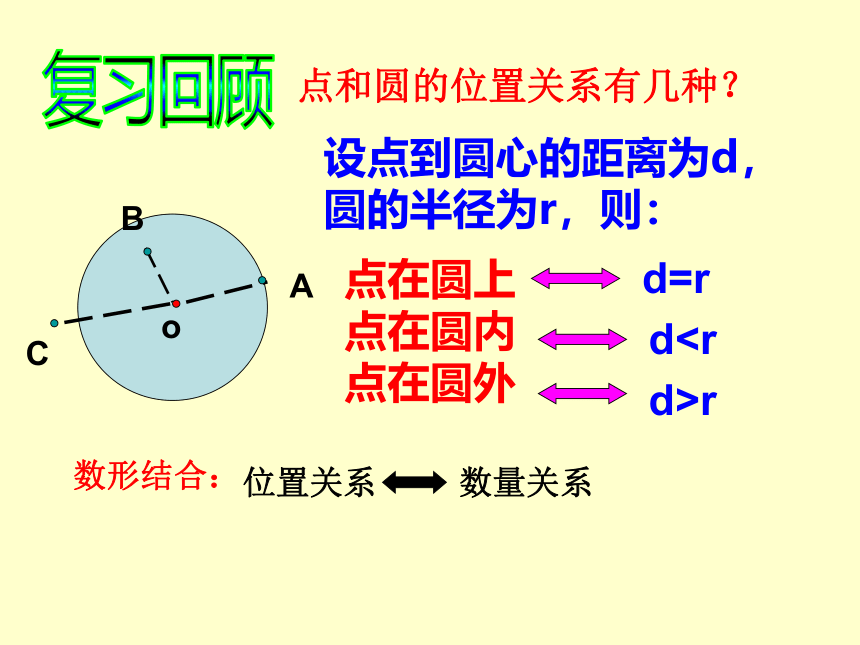
课件20张PPT。3.6(1)直线和圆的位置关系点和圆的位置关系有几种? 设点到圆心的距离为d,圆的半径为r,则:复习回顾点在圆上
点在圆内
点在圆外位置关系数形结合:数量关系od=rdr直线和圆的位置关系有几种?探索新知下面先请同学们欣赏美丽的
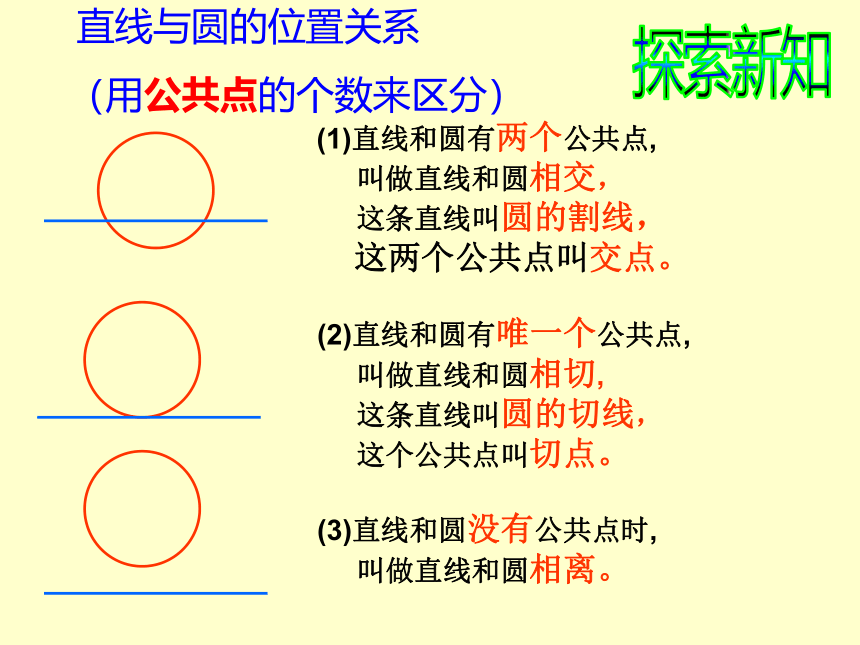
海上日出(地平线)a(地平线)从海上日出这种自然现象中是否可以得到直线和圆的位置关系?(2)直线和圆有唯一个公共点,
叫做直线和圆相切,
这条直线叫圆的切线,
这个公共点叫切点。(1)直线和圆有两个公共点,
叫做直线和圆相交,
这条直线叫圆的割线,
这两个公共点叫交点。(3)直线和圆没有公共点时,
叫做直线和圆相离。 直线与圆的位置关系
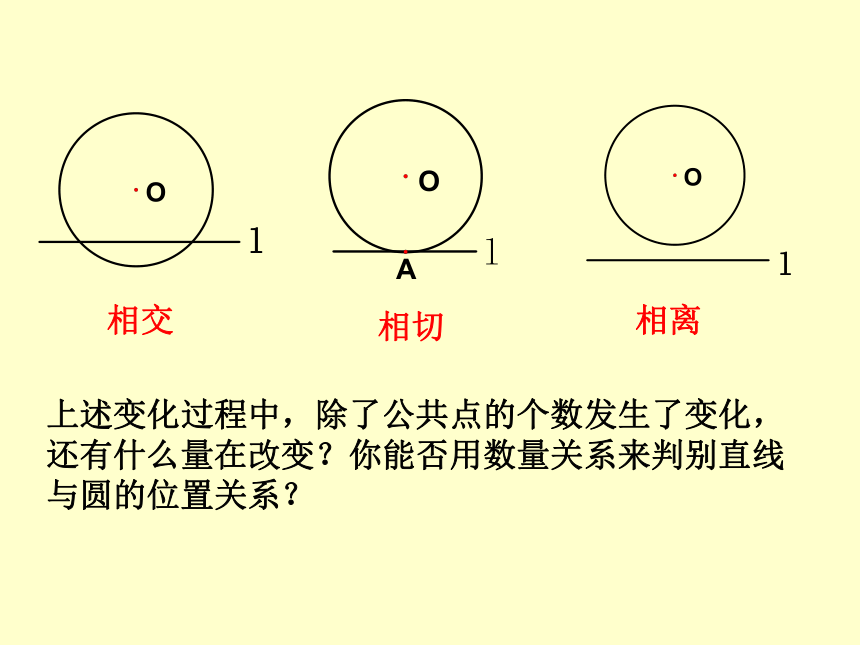
(用公共点的个数来区分)探索新知相交相切相离上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?直线和圆相交d< r直线和圆相切d= r直线和圆相离d> rrd∟rd∟rd 直线和圆的位置关系
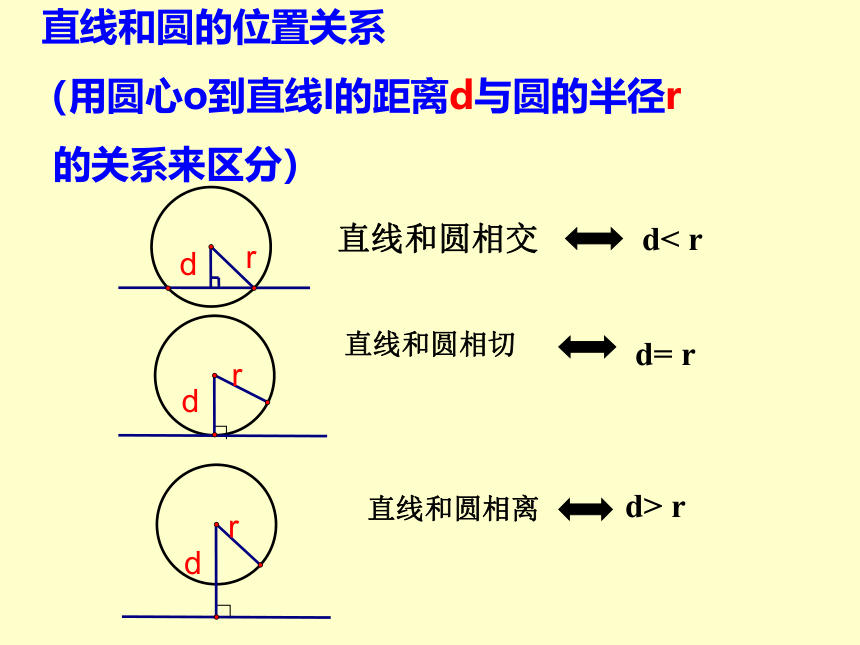
(用圆心o到直线l的距离d与圆的半径r
的关系来区分)相交相切相离d > 5cmd = 5cmd < 5cm小试牛刀0cm≤2103、直线L和⊙O有公共点,则直线L与⊙O( ).
A、相离;B、相切;C、相交;D、相切或相交。D1、已知:圆的直径为13cm,如果直线和 圆心的距离为以下值时,直线和圆有几个 公共点?为什么?(1) 4.5cmA 0 个; B 1个; C 2个;答案:C(2) 6.5cm答案:B(3) 8cm答案:AA 0 个; B 1个; C 2个;A 0 个; B 1个; C 2个;自我检验例:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB
有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm.分析:要了解AB与⊙C的位置
关系,只要知道圆心C到AB的
距离d与r的关系.已知r,只需
求出C到AB的距离d。
d典例讲解解:过C作CD⊥AB,垂足为D在△ABC中,AB=5根据三角形的面积公式有∴即圆心C到AB的距离d=2.4cm所以 (1)当r=2cm时,有d>r,因此⊙C和AB相离。d(2)当r=2.4cm时,有d=r,因此⊙C和AB相切。(3)当r=3cm时,有d(-3,-4),则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是_____。BC43相离相切-1-1拓展.(-3,-4)OBC43-1-1若⊙A要与x轴相切,则⊙A该向上移动多少个单位?若⊙A要与x轴相交呢?思考讨论 在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,
以C为圆心,r为半径作圆。
①当r满足 时, 直线AB与⊙C相离。
②当r满足 时,直线AB与⊙C相切。
③当r满足 时,直线AB与⊙C相交。
130﹤r﹤r=r﹥5CD= cm小结:1、直线与圆的位置关系:0d>r1d=r切点切线2d 的个数来判断;(2)根据性质,由_________________
的关系来判断。两直线与圆的公共点圆心到直线的距离d与半径r
3.切线的性质:
圆的切线垂直于过切点的直径(半径)B符号表示:
连接OA ∵AB是⊙O的切线
∴OA⊥AB(或∠OAB=900)2、判定直线 与圆的位置关系的方法有____种:(1)根据定义,由__________________的个数来判断;(2)根据性质,由_____________________ ______________的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r观察太阳落山的照片,在太阳落山的过程中,太阳与地平线(直线a)经历了哪些位置关系的变化?
a(地平线)
点在圆内
点在圆外位置关系数形结合:数量关系od=rd
海上日出(地平线)a(地平线)从海上日出这种自然现象中是否可以得到直线和圆的位置关系?(2)直线和圆有唯一个公共点,
叫做直线和圆相切,
这条直线叫圆的切线,
这个公共点叫切点。(1)直线和圆有两个公共点,
叫做直线和圆相交,
这条直线叫圆的割线,
这两个公共点叫交点。(3)直线和圆没有公共点时,
叫做直线和圆相离。 直线与圆的位置关系
(用公共点的个数来区分)探索新知相交相切相离上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?直线和圆相交d< r直线和圆相切d= r直线和圆相离d> rrd∟rd∟rd 直线和圆的位置关系
(用圆心o到直线l的距离d与圆的半径r
的关系来区分)相交相切相离d > 5cmd = 5cmd < 5cm小试牛刀0cm≤2103、直线L和⊙O有公共点,则直线L与⊙O( ).
A、相离;B、相切;C、相交;D、相切或相交。D1、已知:圆的直径为13cm,如果直线和 圆心的距离为以下值时,直线和圆有几个 公共点?为什么?(1) 4.5cmA 0 个; B 1个; C 2个;答案:C(2) 6.5cm答案:B(3) 8cm答案:AA 0 个; B 1个; C 2个;A 0 个; B 1个; C 2个;自我检验例:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB
有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm.分析:要了解AB与⊙C的位置
关系,只要知道圆心C到AB的
距离d与r的关系.已知r,只需
求出C到AB的距离d。
d典例讲解解:过C作CD⊥AB,垂足为D在△ABC中,AB=5根据三角形的面积公式有∴即圆心C到AB的距离d=2.4cm所以 (1)当r=2cm时,有d>r,因此⊙C和AB相离。d(2)当r=2.4cm时,有d=r,因此⊙C和AB相切。(3)当r=3cm时,有d
以C为圆心,r为半径作圆。
①当r满足 时, 直线AB与⊙C相离。
②当r满足 时,直线AB与⊙C相切。
③当r满足 时,直线AB与⊙C相交。
130﹤r﹤r=r﹥5CD= cm小结:1、直线与圆的位置关系:0d>r1d=r切点切线2d
3.切线的性质:
圆的切线垂直于过切点的直径(半径)B符号表示:
连接OA ∵AB是⊙O的切线
∴OA⊥AB(或∠OAB=900)2、判定直线 与圆的位置关系的方法有____种:(1)根据定义,由__________________的个数来判断;(2)根据性质,由_____________________ ______________的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r观察太阳落山的照片,在太阳落山的过程中,太阳与地平线(直线a)经历了哪些位置关系的变化?
a(地平线)
