3.6.3切线的判定定理课件
图片预览



文档简介
课件15张PPT。3.6(3) 直线和圆的位置关系
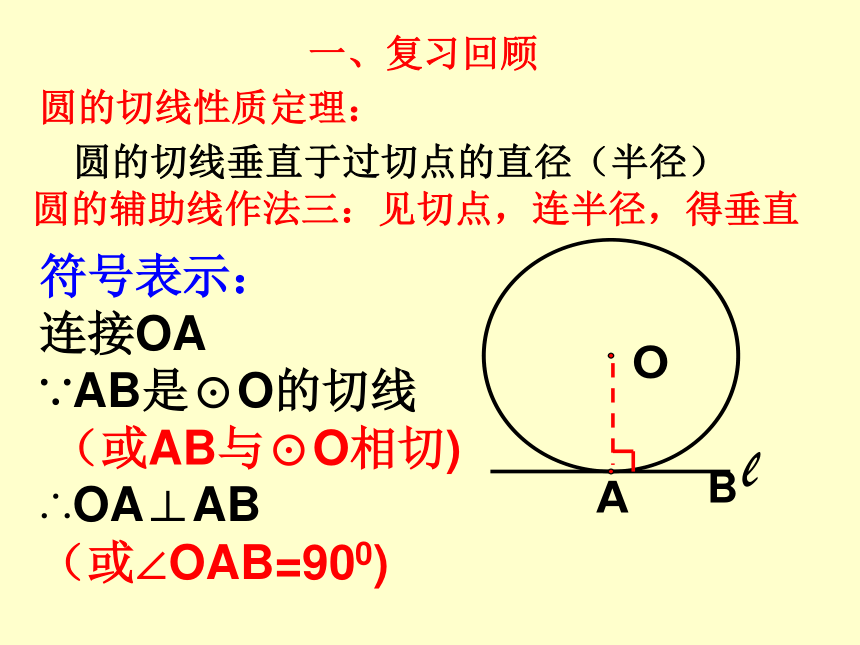
——圆的切线判定定理圆的切线性质定理:B符号表示:
连接OA
∵AB是⊙O的切线
(或AB与⊙O相切)
∴OA⊥AB
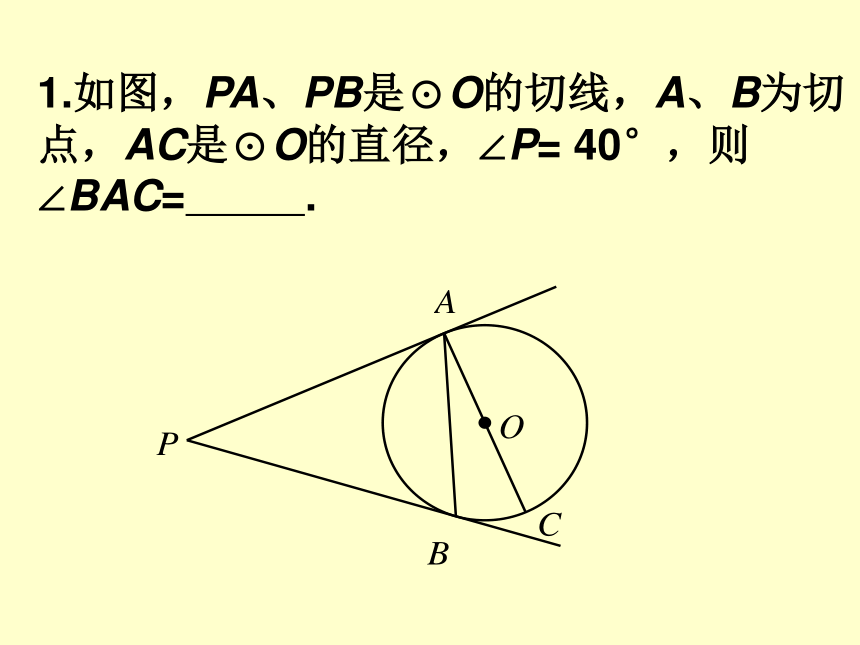
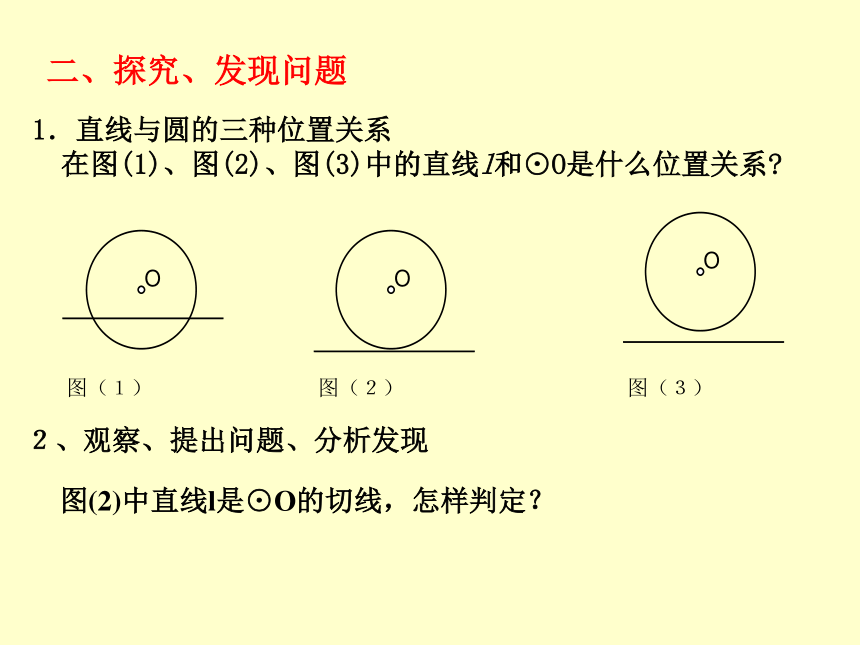
(或∠OAB=900)圆的切线垂直于过切点的直径(半径)圆的辅助线作法三:见切点,连半径,得垂直一、复习回顾1.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P= 40°,则∠BAC= .2.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P= 40°,则∠BAC= .1.直线与圆的三种位置关系
在图(1)、图(2)、图(3)中的直线l和⊙O是什么位置关系?
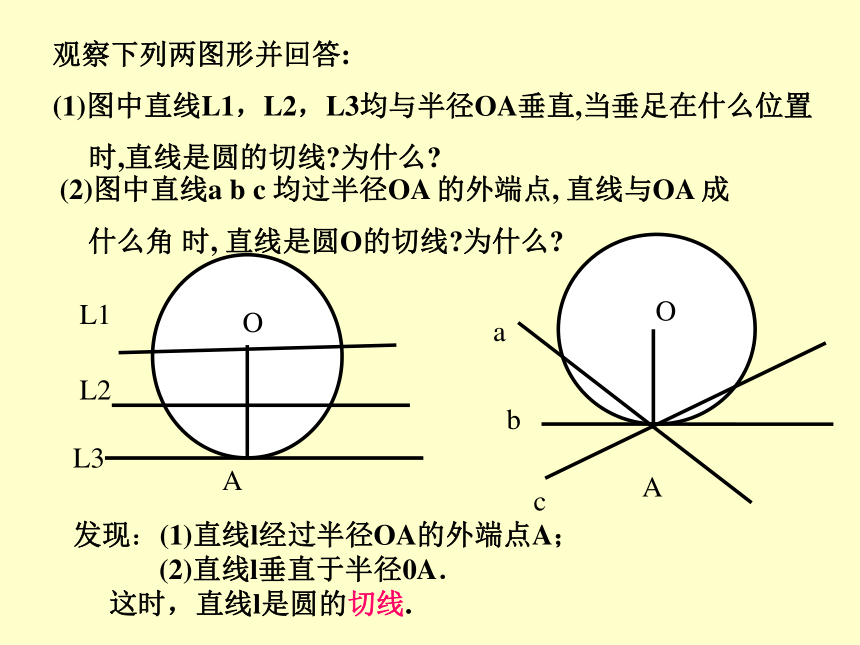
2、观察、提出问题、分析发现 二、探究、发现问题图(2)中直线l是⊙O的切线,怎样判定?观察下列两图形并回答:
(1)图中直线L1,L2,L3均与半径OA垂直,当垂足在什么位置
时,直线是圆的切线?为什么?A(2)图中直线a b c 均过半径OA 的外端点, 直线与OA 成
什么角 时, 直线是圆O的切线?为什么?发现:(1)直线l经过半径OA的外端点A;
(2)直线l垂直于半径0A.
这时,直线l是圆的切线.(二)圆的切线的判定定理:
过半径外端且垂直于半径的直线是圆的切线切线需满足两条件: ①经过半径外端;
②垂直于这条半径. 问题:定理中的两个条件缺少一个行不行? 图(1)中直线l经过半径外端,但不与半径垂直;图(2)(3)中直线l与半径垂直,但不经过半径外端.
从以上反例可以看出,只满足其中一个条件的直线不是圆的切线.必需同时满足,二者缺一不可
做一做:
已知⊙O有一点A,过点A作出⊙O的切线.O.
A例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线
分析:欲证AB是⊙O的切线.由于AB过圆上点C,若连结OC,则AB过半径OC的外端,只需证明OC⊥OB.
.
证明:连结0C
∵0A=0B,CA=CB,
∴0C是等腰△0AB底边AB上的中线.
∴AB⊥OC.
∴ AB是⊙O的切线.
(直线AB经过半径0C的外端C,并且垂直于半径0C)例2 : 如图,已知OA=OB=5厘米,AB=8厘米,⊙O的直径为6厘米.求证:AB与⊙O相切例3.如图所示,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为2的⊙A与OM相切与点B,连接BA并延长交⊙A于点D,交ON于点E.
求证:ON是⊙A的切线想一想:
以上两例辅助线的做法是否相同?有什么规律呢?圆的辅助线作法四(证切线):
(1)若直线与圆有公共点时,
辅助线的作法是 “连半径,证垂直”.
(2)若直线与圆没有明确有公共点时,
辅助线的作法是“作垂线,证半径”.练习:
1.如图所示,AB是⊙O的直径,D为⊙O上
一点,AT平分∠BAD交⊙O于点T,过T
作AD的垂线交AD的延长线于点C.
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,
CT= ,
求AD的长.练习:
2.如图所示,O为正方形ABCD对角线上一点,以O为圆心,OA的长为半径的⊙O与BC相切于M,与AB、AD分别相交于E、F. (1)求证:CD与⊙O相切; (2)若⊙O的半径为,
求正方形ABCD的边长
——圆的切线判定定理圆的切线性质定理:B符号表示:
连接OA
∵AB是⊙O的切线
(或AB与⊙O相切)
∴OA⊥AB
(或∠OAB=900)圆的切线垂直于过切点的直径(半径)圆的辅助线作法三:见切点,连半径,得垂直一、复习回顾1.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P= 40°,则∠BAC= .2.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P= 40°,则∠BAC= .1.直线与圆的三种位置关系
在图(1)、图(2)、图(3)中的直线l和⊙O是什么位置关系?
2、观察、提出问题、分析发现 二、探究、发现问题图(2)中直线l是⊙O的切线,怎样判定?观察下列两图形并回答:
(1)图中直线L1,L2,L3均与半径OA垂直,当垂足在什么位置
时,直线是圆的切线?为什么?A(2)图中直线a b c 均过半径OA 的外端点, 直线与OA 成
什么角 时, 直线是圆O的切线?为什么?发现:(1)直线l经过半径OA的外端点A;
(2)直线l垂直于半径0A.
这时,直线l是圆的切线.(二)圆的切线的判定定理:
过半径外端且垂直于半径的直线是圆的切线切线需满足两条件: ①经过半径外端;
②垂直于这条半径. 问题:定理中的两个条件缺少一个行不行? 图(1)中直线l经过半径外端,但不与半径垂直;图(2)(3)中直线l与半径垂直,但不经过半径外端.
从以上反例可以看出,只满足其中一个条件的直线不是圆的切线.必需同时满足,二者缺一不可
做一做:
已知⊙O有一点A,过点A作出⊙O的切线.O.
A例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线
分析:欲证AB是⊙O的切线.由于AB过圆上点C,若连结OC,则AB过半径OC的外端,只需证明OC⊥OB.
.
证明:连结0C
∵0A=0B,CA=CB,
∴0C是等腰△0AB底边AB上的中线.
∴AB⊥OC.
∴ AB是⊙O的切线.
(直线AB经过半径0C的外端C,并且垂直于半径0C)例2 : 如图,已知OA=OB=5厘米,AB=8厘米,⊙O的直径为6厘米.求证:AB与⊙O相切例3.如图所示,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为2的⊙A与OM相切与点B,连接BA并延长交⊙A于点D,交ON于点E.
求证:ON是⊙A的切线想一想:
以上两例辅助线的做法是否相同?有什么规律呢?圆的辅助线作法四(证切线):
(1)若直线与圆有公共点时,
辅助线的作法是 “连半径,证垂直”.
(2)若直线与圆没有明确有公共点时,
辅助线的作法是“作垂线,证半径”.练习:
1.如图所示,AB是⊙O的直径,D为⊙O上
一点,AT平分∠BAD交⊙O于点T,过T
作AD的垂线交AD的延长线于点C.
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,
CT= ,
求AD的长.练习:
2.如图所示,O为正方形ABCD对角线上一点,以O为圆心,OA的长为半径的⊙O与BC相切于M,与AB、AD分别相交于E、F. (1)求证:CD与⊙O相切; (2)若⊙O的半径为,
求正方形ABCD的边长
