第23章图形的相似 单元测试(含答案)2024-2025学年华东师大版数学九年级上册
文档属性
| 名称 | 第23章图形的相似 单元测试(含答案)2024-2025学年华东师大版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 85.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 15:58:01 | ||
图片预览


文档简介
华东师大版九年级上 第23章 图形的相似 单元测试
一.选择题(共12小题)
1.a、b、c、d是成比例线段,其中a=6cm,b=3cm,c=4cm,则线段d的长可能为( )
A.2cm B.3cm C.4cm D.5cm
2.在平面直角坐标系中,点P(2,-3)关于原点的对称点P′的坐标是( )
A.(2,3) B.(-2,-3) C.(2,-3) D.(-2,3)
3.若点C是线段AB的黄金分割点,且AB=2,则BC=( )
A. B. C. D.或
4.如图,点D、E分别是△ABC边AB、AC上的点,下列比例式中,能判定DE∥BC的是( )
A. B. C. D.
5.已知△ABC与△DEF相似且面积比为,则周长比为( )
A. B. C. D.
6.若△ABC∽△DEF,△ABC与△DEF的面积比为1:16,则AB与DE的比是( )
A.1:4 B.1:8 C.1:16 D.1:32
7.如图,△ABC与△DEF是位似图形,点O是位似中心,若位似比2:3,C△ABC=4,则C△DEF等于( )
A.6 B.8 C.9 D.12
8.已知△ABC和△DEF中,,则△ABC与△DEF的周长之比为( )
A. B. C. D.
9.如图,在平行四边形ABCD中,E是DC上的点,DE:EC=3:2,连接AE交BD于点F,则△DEF与△DAF的面积之比为( )
A.2:5 B.3:5 C.4:25 D.9:25
10.如图,直线a∥b∥c,分别交直线m、n于点A、C、E、B、D、F,下列结论不正确的是( )
A. B. C. D.
11.如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
A. B. C. D.
12.如图,在正方形ABCD中,点E为正方形内部一点,连接AE、BE,将线段AE绕点A逆时针旋转90°得到线段AF,点F落在BE的延长线上,BE的延长线交AD于点M,连接CF交BD于点N,若AM:AB=1:3,则的值为( )
A. B. C. D.
二.填空题(共5小题)
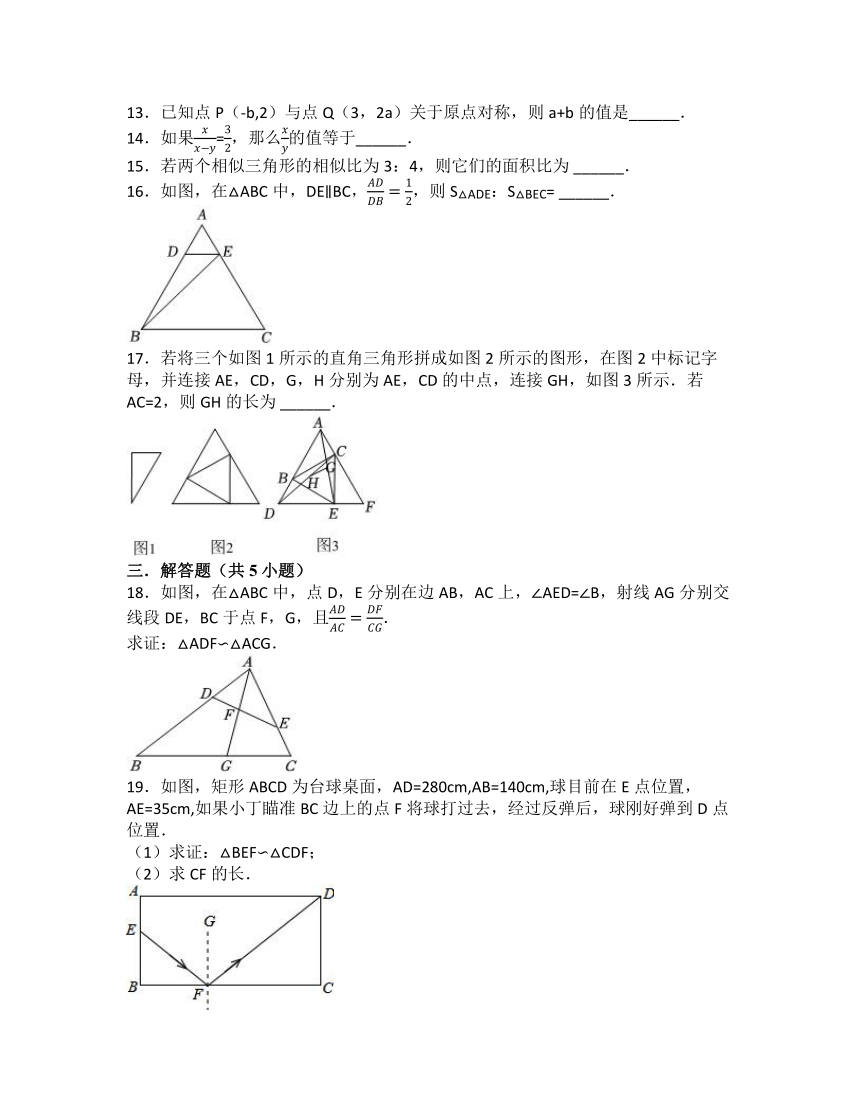
13.已知点P(-b,2)与点Q(3,2a)关于原点对称,则a+b的值是______.
14.如果=,那么的值等于______.
15.若两个相似三角形的相似比为3:4,则它们的面积比为 ______.
16.如图,在△ABC中,DE∥BC,,则S△ADE:S△BEC= ______.
17.若将三个如图1所示的直角三角形拼成如图2所示的图形,在图2中标记字母,并连接AE,CD,G,H分别为AE,CD的中点,连接GH,如图3所示.若AC=2,则GH的长为 ______.
三.解答题(共5小题)
18.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.
求证:△ADF∽△ACG.
19.如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
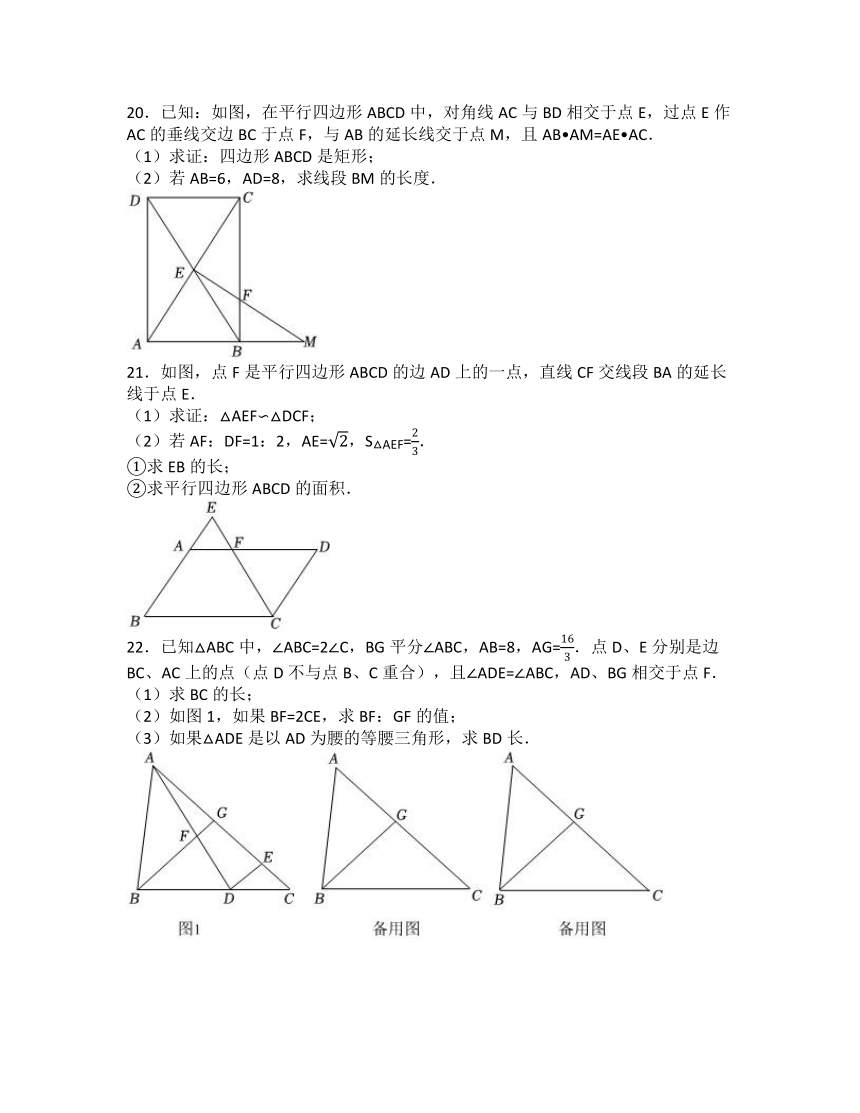
20.已知:如图,在平行四边形ABCD中,对角线AC与BD相交于点E,过点E作AC的垂线交边BC于点F,与AB的延长线交于点M,且AB AM=AE AC.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,AD=8,求线段BM的长度.
21.如图,点F是平行四边形ABCD的边AD上的一点,直线CF交线段BA的延长线于点E.
(1)求证:△AEF∽△DCF;
(2)若AF:DF=1:2,AE=,S△AEF=.
①求EB的长;
②求平行四边形ABCD的面积.
22.已知△ABC中,∠ABC=2∠C,BG平分∠ABC,AB=8,AG=.点D、E分别是边BC、AC上的点(点D不与点B、C重合),且∠ADE=∠ABC,AD、BG相交于点F.
(1)求BC的长;
(2)如图1,如果BF=2CE,求BF:GF的值;
(3)如果△ADE是以AD为腰的等腰三角形,求BD长.
华东师大版九年级上第23章图形的相似单元测试
(参考答案)
一.选择题(共12小题)
1、A 2、D 3、D 4、C 5、A 6、A 7、A 8、B 9、B 10、B 11、B 12、A
二.填空题(共5小题)
13、2; 14、3; 15、9:16; 16、1:6; 17、;
三.解答题(共5小题)
18、证明:∵∠AED=∠B,∠BAC=∠EAD,
∴∠ADE=∠C,
∵=,
∴△ADF∽△ACG.
19、(1)证明:∵∠EFG=∠DFG,
∴∠EFB=∠DFC,
又∵∠B=∠C,
∴△BEF∽△CDF;
(2)解:∵△BEF∽△CDF,
∴=,
设FC=xcm,则=,
解得:x=160,
答:CF的长为160cm.
20、(1)证明:∵AB AM=AE AC,
∴,
∵∠CAB=∠CAB,
∴△ACB∽△AME,
∴∠AEM=∠ABC=90°,
∴平行四边形ABCD是矩形.
(2)解:∵四边形ABCD是矩形,
∴DE=BE,AE=EC,AC=BD,∠DAB=90°,
∴AE=BE=DE=CE,
∵AB=6,AD=8,
∴BD==10,
∴AE=5,
∵AB AM=AE AC,
∴6×(6+BM)=5×10,
∴BM=.
21、(1)证明:∵四边形ABCD是平行四边形,
∴BA∥CD,
∴∠E=∠FCD,∠EAF=∠CDF,
∴△AEF∽△DCF;
(2)解:①由(1)知△AEF∽△DCF,
∴,
∵AF:DF=1:2,AE=,
∴=,
∴DC=2,
∵四边形ABCD是平行四边形,
∴AB=DC,
∴AB=2,
∴BE=AB+AE=3;
②连接AC,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴=,
∵S△AEF=,
∴S△AEC=2,
∵=,
∴S△ABC=4,
∴平行四边形ABCD的面积为8.
22、解:(1)∵∠ABC=2∠C,BG平分∠ABC,
∴∠ABG=∠BGC=∠C,
∴BG=CG,
又∵∠BAG=∠CAB,
∴△ABG∽△ACB,
∴==,
∴AC===12,
∴CG=AC-AG=,
∴BC==10;
(2)由(1)知,△ABG∽△CAB,
∴∠AGB=∠ABC,
∵∠ADE=∠ABC,
∴∠AGB=∠ADE,
∵∠FAG=∠DAE,
∴∠AFG=∠AED,
∵∠AFG+∠AFB=180°,∠AED+∠CED=180°,
∴∠AFG=∠CED,
又∵∠ABG=∠C,
∴△ABF∽△DCE,
∴==2,
∴CD=4,
∴BD=BC-CD=6,
过G作HG∥BC交AD于H,如图:
∴=,
∴GH==,
同理,==,
∴BF:FG=;
(3)∵AD=AE,
∴∠ADE=∠AED=∠ABC=∠AGB,
∴DE∥BG,
∴∠AFG=∠ADE=∠AGF,
∴AF=AG,
∵∠ABC=2∠C,
∴∠EDC=∠C,
∴CE=DE,
由(2)知,△ABF∽△CDE,
∴AF=BF,
∴GF=BG-BF=CG-AG=,
∵DE∥BG,
∴=,
∴DE=CE=,
同理,=,
∴CD=,
∴BD=.
另外,DA=DE时,作CE中垂线交BC于点H,同理可证得△ABD≌△DHE.此时BD=1.
一.选择题(共12小题)
1.a、b、c、d是成比例线段,其中a=6cm,b=3cm,c=4cm,则线段d的长可能为( )
A.2cm B.3cm C.4cm D.5cm
2.在平面直角坐标系中,点P(2,-3)关于原点的对称点P′的坐标是( )
A.(2,3) B.(-2,-3) C.(2,-3) D.(-2,3)
3.若点C是线段AB的黄金分割点,且AB=2,则BC=( )
A. B. C. D.或
4.如图,点D、E分别是△ABC边AB、AC上的点,下列比例式中,能判定DE∥BC的是( )
A. B. C. D.
5.已知△ABC与△DEF相似且面积比为,则周长比为( )
A. B. C. D.
6.若△ABC∽△DEF,△ABC与△DEF的面积比为1:16,则AB与DE的比是( )
A.1:4 B.1:8 C.1:16 D.1:32
7.如图,△ABC与△DEF是位似图形,点O是位似中心,若位似比2:3,C△ABC=4,则C△DEF等于( )
A.6 B.8 C.9 D.12
8.已知△ABC和△DEF中,,则△ABC与△DEF的周长之比为( )
A. B. C. D.
9.如图,在平行四边形ABCD中,E是DC上的点,DE:EC=3:2,连接AE交BD于点F,则△DEF与△DAF的面积之比为( )
A.2:5 B.3:5 C.4:25 D.9:25
10.如图,直线a∥b∥c,分别交直线m、n于点A、C、E、B、D、F,下列结论不正确的是( )
A. B. C. D.
11.如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
A. B. C. D.
12.如图,在正方形ABCD中,点E为正方形内部一点,连接AE、BE,将线段AE绕点A逆时针旋转90°得到线段AF,点F落在BE的延长线上,BE的延长线交AD于点M,连接CF交BD于点N,若AM:AB=1:3,则的值为( )
A. B. C. D.
二.填空题(共5小题)
13.已知点P(-b,2)与点Q(3,2a)关于原点对称,则a+b的值是______.
14.如果=,那么的值等于______.
15.若两个相似三角形的相似比为3:4,则它们的面积比为 ______.
16.如图,在△ABC中,DE∥BC,,则S△ADE:S△BEC= ______.
17.若将三个如图1所示的直角三角形拼成如图2所示的图形,在图2中标记字母,并连接AE,CD,G,H分别为AE,CD的中点,连接GH,如图3所示.若AC=2,则GH的长为 ______.
三.解答题(共5小题)
18.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.
求证:△ADF∽△ACG.
19.如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
20.已知:如图,在平行四边形ABCD中,对角线AC与BD相交于点E,过点E作AC的垂线交边BC于点F,与AB的延长线交于点M,且AB AM=AE AC.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,AD=8,求线段BM的长度.
21.如图,点F是平行四边形ABCD的边AD上的一点,直线CF交线段BA的延长线于点E.
(1)求证:△AEF∽△DCF;
(2)若AF:DF=1:2,AE=,S△AEF=.
①求EB的长;
②求平行四边形ABCD的面积.
22.已知△ABC中,∠ABC=2∠C,BG平分∠ABC,AB=8,AG=.点D、E分别是边BC、AC上的点(点D不与点B、C重合),且∠ADE=∠ABC,AD、BG相交于点F.
(1)求BC的长;
(2)如图1,如果BF=2CE,求BF:GF的值;
(3)如果△ADE是以AD为腰的等腰三角形,求BD长.
华东师大版九年级上第23章图形的相似单元测试
(参考答案)
一.选择题(共12小题)
1、A 2、D 3、D 4、C 5、A 6、A 7、A 8、B 9、B 10、B 11、B 12、A
二.填空题(共5小题)
13、2; 14、3; 15、9:16; 16、1:6; 17、;
三.解答题(共5小题)
18、证明:∵∠AED=∠B,∠BAC=∠EAD,
∴∠ADE=∠C,
∵=,
∴△ADF∽△ACG.
19、(1)证明:∵∠EFG=∠DFG,
∴∠EFB=∠DFC,
又∵∠B=∠C,
∴△BEF∽△CDF;
(2)解:∵△BEF∽△CDF,
∴=,
设FC=xcm,则=,
解得:x=160,
答:CF的长为160cm.
20、(1)证明:∵AB AM=AE AC,
∴,
∵∠CAB=∠CAB,
∴△ACB∽△AME,
∴∠AEM=∠ABC=90°,
∴平行四边形ABCD是矩形.
(2)解:∵四边形ABCD是矩形,
∴DE=BE,AE=EC,AC=BD,∠DAB=90°,
∴AE=BE=DE=CE,
∵AB=6,AD=8,
∴BD==10,
∴AE=5,
∵AB AM=AE AC,
∴6×(6+BM)=5×10,
∴BM=.
21、(1)证明:∵四边形ABCD是平行四边形,
∴BA∥CD,
∴∠E=∠FCD,∠EAF=∠CDF,
∴△AEF∽△DCF;
(2)解:①由(1)知△AEF∽△DCF,
∴,
∵AF:DF=1:2,AE=,
∴=,
∴DC=2,
∵四边形ABCD是平行四边形,
∴AB=DC,
∴AB=2,
∴BE=AB+AE=3;
②连接AC,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴=,
∵S△AEF=,
∴S△AEC=2,
∵=,
∴S△ABC=4,
∴平行四边形ABCD的面积为8.
22、解:(1)∵∠ABC=2∠C,BG平分∠ABC,
∴∠ABG=∠BGC=∠C,
∴BG=CG,
又∵∠BAG=∠CAB,
∴△ABG∽△ACB,
∴==,
∴AC===12,
∴CG=AC-AG=,
∴BC==10;
(2)由(1)知,△ABG∽△CAB,
∴∠AGB=∠ABC,
∵∠ADE=∠ABC,
∴∠AGB=∠ADE,
∵∠FAG=∠DAE,
∴∠AFG=∠AED,
∵∠AFG+∠AFB=180°,∠AED+∠CED=180°,
∴∠AFG=∠CED,
又∵∠ABG=∠C,
∴△ABF∽△DCE,
∴==2,
∴CD=4,
∴BD=BC-CD=6,
过G作HG∥BC交AD于H,如图:
∴=,
∴GH==,
同理,==,
∴BF:FG=;
(3)∵AD=AE,
∴∠ADE=∠AED=∠ABC=∠AGB,
∴DE∥BG,
∴∠AFG=∠ADE=∠AGF,
∴AF=AG,
∵∠ABC=2∠C,
∴∠EDC=∠C,
∴CE=DE,
由(2)知,△ABF∽△CDE,
∴AF=BF,
∴GF=BG-BF=CG-AG=,
∵DE∥BG,
∴=,
∴DE=CE=,
同理,=,
∴CD=,
∴BD=.
另外,DA=DE时,作CE中垂线交BC于点H,同理可证得△ABD≌△DHE.此时BD=1.
