点与圆的位置关系

24.2.1点与圆的位置关系（一）
学习目标：
1．理解并掌握设⊙O的半径为r，点P到圆心的距离OP=d，则有：点P在圆外d>r；点P在圆上d=r；点P在圆内d2．理解不在同一直线上的三个点确定一个圆并掌握它的运用．
3．了解三角形的外接圆和三角形外心的概念．
学习重点：
点和圆的位置关系的结论：不在同一直线上的三个点确定一个圆其它们的运用．
学习过程
一、复习
1,圆的定义是什么？____________________________
2,线段的垂直平分线的性质:_______________________
二、探索新知
1, 设⊙O的半径为r，点P到圆心的距离为OP=d
则有：点P在圆外_________(d与r的大小关系)
点P在圆上_________
点P在圆内_________
2,反过来，也十分明显，如果d>r点P在_______；如果d=r点P在_______；如果d3, 因此，我们可以得到：设⊙O的半径为r，点P到圆的距离为d，则有：点P在圆外_____，点P在圆上____，点P在圆内_____
4,如图已知矩形ABCD的边AB=3厘米，AD=4厘米
（1）以点A为圆心，3厘米为半径作⊙A，则点B、C、D与⊙A的位置关系如何？
（2）以点A为圆心，4厘米为半径作⊙A，则点B、C、D与⊙A的位置关系如何？
（3）以点A为圆心，5厘米为半径作⊙A，则点B、C、D与⊙A的位置关系如何？
5,画一画
(1),平面上有一点A，经过已知A点的圆有几个？
(2),平面上有两点A、B，经过已知点A、B的圆有几个？它们的圆心分布有什么特点？
(3),平面上有三点A、B、C，经过A、B、C三点的圆有几个？圆心在哪里？
(4),第三种情况的作法：
①连接AB、BC；
②分别作线段AB、BC的_________________________________；
③以___为圆心，以___为半径作圆，____就是所要求作的圆．
6,所以经过A、B、C三点可以作一个圆，并且只能作一个圆．
即：______________________________确定一个圆.
7, 经过三角形的三个顶点可以做一个圆，并且只能画一个圆，这个圆叫做三角形的_______．外接圆的圆心是_____________________________，叫做这个三角形的_______．
三角形的外心就是三角形三条边的________的交点，它到三角形三个顶点的__________。
三,练一练：
1，经过A，B两点的圆的圆心在_________________________
2,_______________________________________确定一个圆.
3,与三角形三个顶点距离相等的点,在这个三角形的 ( )
A,三条中线的交点. B, 三条角平分线的交点.
C, 三条高的交点 D, 三边垂直平分线的交点
4，判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆 ( ).
(2)经过三点一定可以确定一个圆 ( )
(3)三角形的外心到三角形各顶点的距离相等 ( )
5,青岛国际帆船中心要建一处公共服务设施,使它到三处运动员公寓A,B,C的距离相等.
(1),三所运动员公寓A,B,C的位置如图所示,请你在图中确定这醋公共服务设施的位置.用点P表示.
(2)如果∠BAC=66°,则∠BPC=_____.
24.2.1点与圆的位置关系（二）
学习目标:
了解间接证明的一种基本方法——反证法；了解反证法的思考过程、特点
学习重点：
会用反证法证明问题；了解反证法的思考过程.
一,复习，引入新课
1.______________________________的三个点确定一个圆.
2. 提出问题：我们知道这样一个命题：“过在同一直线上的三点A、B、C不能作圆”. 讨论如何证明这个命题？
二、学习反证法：
1.给出证法：先假设可以作一个⊙O过A、B、C三点，
则O在AB的中垂线l1上，O又在BC的中垂线l2上，
即O是l1与l2的交点。
但 ∵A、B、C共线，∴l1∥l2 (矛盾)
∴ 过在同一直线上的三点A、B、C不能作圆.
2.关于反证法:
(1),反证法的思路：一般地，假设原命题不成立，经过正确的推理，最后得出矛盾，因此说明假设错误，从而证明了原命题成立.
(2).证明基本步骤：假设原命题的结论不成立 → 从假设出发，经推理论证得到矛盾 → 矛盾的原因是假设不成立，从而原命题的结论成立
(3).应用关键：在正确的推理下得出矛盾（与已知条件矛盾，或与假设矛盾，或与定义、公理、定理、事实矛盾等）.
(4).方法实质：反证法是利用互为逆否的命题具有等价性来进行证明的，即由一个命题与其逆否命题同真假，通过证明一个命题的逆否命题的正确，从而肯定原命题真实.
3. 试一试：
证明:两直线平行,同位角相等.
分析：
如何假设原命题的结论不成立？ → 如何从假设出发进行推理？ → 得到怎样的矛盾？
三,小结：
反证法是从否定结论入手，经过一系列的逻辑推理，得出矛盾，从而说明原结论正确.
四、练习：
1,练习：教材P93 4题
2, 用反证法证明“一个三角形中必有一个内角小于或等于60度”，该如何假设？这个问题没有讲解清楚。
3,证明:有两个内角为60°的三角形是等边三角形.
24.2．2直线与圆有关的位置关系(一)
学习目标
（1）了解直线和圆的位置关系的有关概念．
（2）理解设⊙O的半径为r，直线L到圆心O的距离为d，则有：
直线L和⊙O相交dr．
学习重点
2．重点：由上节课点和圆的位置关系迁移并运动直线导出直线和圆的位置关系的三个对应等价．
学习过程
一，复习引入
点P在圆外____,点P在圆上____, 点P在圆内____.
二、探索新知
活动1：P93页思考：把海平面看作一条直线，太阳看作一个圆，由此你能得出直线与圆的位置关系吗？
由此你能归纳出直线和圆有几种位置关系吗？
( http: / / )
如图（a），直线L和圆有____公共点，这时我们就说这条直线和圆____，这条直线叫做圆的____．
如图（b），直线和圆有____公共点，这时我们说这条直线和圆____，这条直线叫做圆的____，这个点叫做______．
如图（c），直线和圆____公共点，这时我们说这条直线和圆相离．
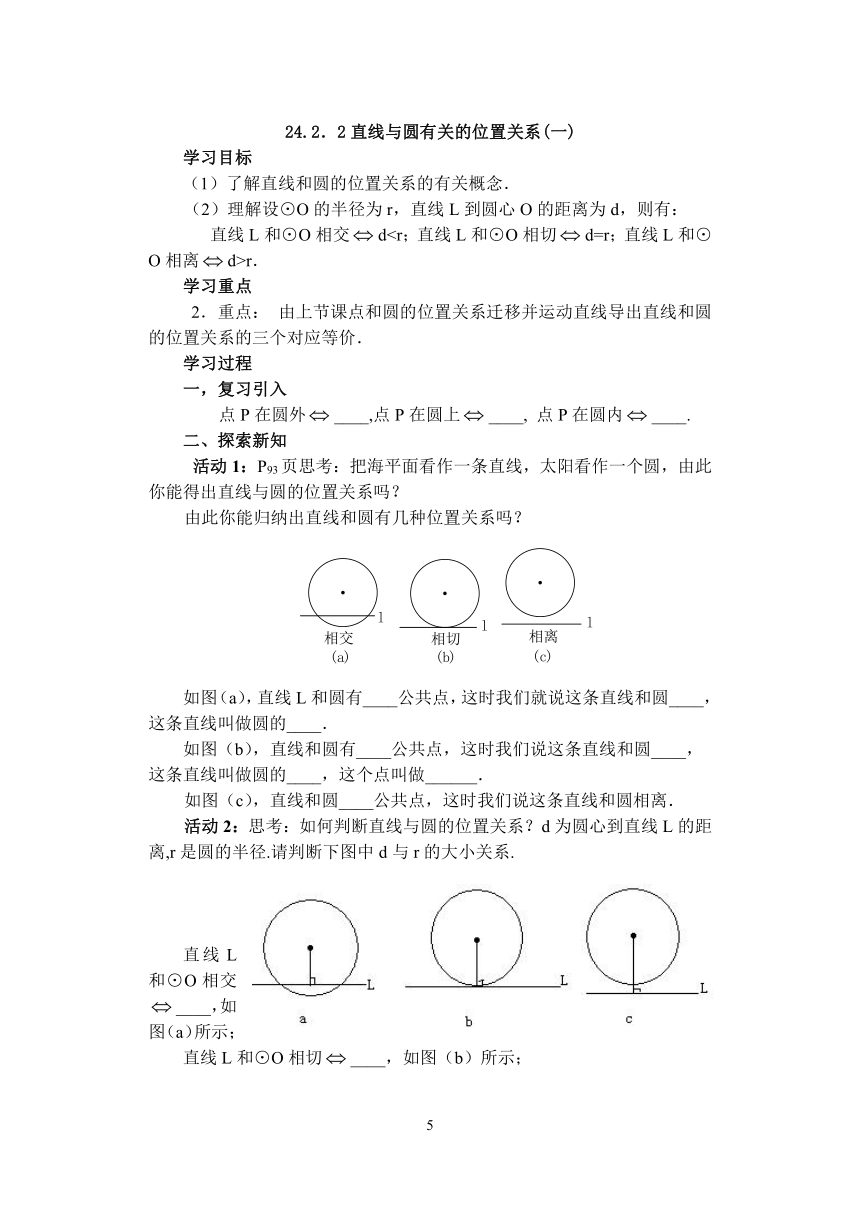
活动2：思考：如何判断直线与圆的位置关系？d为圆心到直线L的距离,r是圆的半径.请判断下图中d与r的大小关系.
直线L和⊙O相交____，如图（a）所示；
直线L和⊙O相切____，如图（b）所示；
直线L和⊙O相离____，如图（c）所示．（
小结：直线与圆的位置关系
直线与圆的位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
活动4、
1、已知⊙O的半径为5cm，O到直线a的距离为3cm，则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm，O到直线a的距离是4cm，则⊙O与直线a的位置关系是 ___ _。
3、已知⊙O的半径为6cm，O到直线a的距离为7cm，则直线a与⊙O的公共点个数是____。
4、已知⊙O的直径是6cm，O到直线a的距离是4cm，则⊙O与直线a的位置关系是 ___ _。
5、设⊙O的半径为4，点O到直线a的距离为d，若⊙O与直线a至多只有一个公共点，则d为（ ）
A、d≤4 B、d＜4 C、d≥4 D、d＝4
6、设⊙p的半径为4cm，直线l上一点A到圆心的距离为4cm，则直线l与⊙O的位置关系是……………………………………………（ ）
A、相交 B、相切 C、相离 D、相切或相交
三、归纳总结：1、直线与圆的位置关系3种：相离、相切和相交。
2、识别直线与圆的位置关系的方法：
（1）一种是根据定义进行识别：
直线L与⊙o没有公共点 直线L与⊙o相离。
直线L与⊙o只有一个公共点 直线L与⊙o相切。
直线L与⊙o有两个公共点 直线L与⊙o相交。
（2）另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别：
d>r 直线L与⊙o相离；
d=r 直线L与⊙o相切；
d24.2．2直线与圆有关的位置关系(二)
学习目标:
理解切线的判定定理并熟练掌握以上内容解决一些实际问题．
学习重点: 理解切线的判定定理.
学习过程
一、复习引入：
直线与圆的三中位置关系中，最重要的是直线与圆相切，
二、探索新知：
1、画⊙O及半径OA，画一条直线l过半径OA的外端点，且垂直于OA。你发现直线l与⊙O有怎样的位置关系？为什么？
因为d=r直线L和⊙O相切，(这里的d是圆心O到直线L的距离)并由d=r就可得到L经过半径r的外端，即半径OA的A点，因此，我们可以得到切线的判定定理：
经过半径的_____并且________________的直线是圆的切线.
2, 已知直线是⊙O的切线，切点为A，连接0A，你发现了什么？
结论：(切线的性质定理) 圆的切线______________的半径。
二,切线判定定理的运用
1,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线.
根据上面的判定定理，如果你要证明一条直线是⊙O的切线，你应该如何证明？
应分为两步：
A,说明这个点是______的点，
B,过这点的半径______直线．
证明:连接OC
∵___________,____________.
∴_____________________,_____________________
∴___⊥___.
∴_______________的切线.
2.已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC, ∠A=30.求证:直线AB是⊙O的切线.
作辅助线小结：________________________________________________.
3,作⊙D，判断⊙D与OA的位置关系， 并证明你的结论。
作辅助线小结：________________________________________
4, 练习:课本P96. 第二题
24.2．2直线与圆有关的位置关系(三)
学习目标
1,了解切线长的概念．
2,理解切线长定理，熟练掌握它的应用．
3,复习圆与直线的位置关系和切线的判定定理、性质定理知识迁移到切长线的概念和切线长定理.
学习重难点、关键
1．重点：切线长定理及其运用．
2．难点与关键：切线长定理的导出及其证明和运用切线长定理解决一些实际问题．
学习过程
一、复习引入
经过平面上一个已知点，作已知圆的切线会有怎样的情形？
二、探索新知
1, 过⊙O上任一点A都可以作一条切线，并且只有一条，根据下面提出的问题操作思考并解决这个问题．
问题：在纸上画出⊙O，圆上一点A,圆外一点P.并画出过A点的唯一切线PA，连结PO，沿着直线PO将纸对折，设圆上与点A重合的点为B，这时，OB是⊙O的一条半径吗？PB是⊙O的切线吗？利用图形的轴对称性，说明圆中的PA与PB，∠APO与∠BPO有什么关系？
OB与OA重叠，OA是半径，OB也就是半径了．又因为OB是半径，PB为OB的外端，又根据折叠后的角不变，所以PB是⊙O的又一条切线，根据轴对称性质，我们很容易得到PA=PB，∠APO=∠BPO．
2,我们把PA或PB的长，即经过圆外一点作圆的切线，_______________的线段的长，叫做这点到圆的切线长．
3,切线与切线长的区别______________________________.
4,从上面我们可以得到：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角．
下面，我们证明．
如图，已知PA、PB是⊙O的两条切线．
求证：PA=PB，∠OPA=∠OPB．
证明：∵____,____是⊙O的两条切线．
∴___⊥___，___⊥____
又OA=OB，OP=OP，
∴_____≌Rt_______
∴____=____，____=_____
5,因此，我们得到切线长定理：
从圆外一点可以引圆的两条切线，______________________，这一点和圆心的连线___________________________________.
6,例1、PA、PB是⊙O的两条切线，A、B为切点，直线OP交于⊙O于点D、E，交AB于C。
（1）写出图中所有的垂直关系______________________
（2）写出图中与∠OAC相等的角___________________
（3）写出图中所有的全等三角形____________________
（4）写出图中所有的等腰三角形____________________
7,归纳：切线长定理为证明线段相等，角相等，弧相等，垂直关系提供了理论依据。在解决有关圆的切线长问题时，往往需要我们构建基本图形。
一般需要连接些什么点呢
8,如图所示PA、PB分别切圆O于A、B，并与圆O的切线CD分别相交于C、D，已知
PA=7cm，
(1)求△PCD的周长．
(2) 如果∠P=46°,求∠COD的度数
24.2．2直线与圆有关的位置关系(四)
学习内容:
1、三角形的内切圆及三角形内心的概念．
2、定理及概念的运用。
学习目标:
复习圆与直线的位置关系和切线的判定定理、性质定理知识迁移到切长线的概念和切线长定理，然后根据所学三角形角平分线的性质给出三角形的内切圆和三角形的内心概念，最后应用它们解决一些实际问题．
学习过程：
一、复习引入：
1,角平分线的性质是什么
2,如图是一块三角形木料，木工师傅要从中裁下一块圆形用料，怎样才能使裁下的圆的面积尽可能大呢？
二、探索新知：
1,就上面的问题,要作的圆，使它和已知三角形的各边都相切
已知： △ABC（如图）
求作：和△ABC的各边都相切的圆
问题１：作圆的关键是什么？
问题２：怎样确定圆心的位置
问题３：圆心的位置确定后怎样确定圆的半径？
问题４:在这块三角形材料上还能裁下更大的圆吗
A,与三角形________________________叫做三角形的内切圆.
B,三角形内切圆的圆心叫三角形的_____________.
C,三角形内心的性质：
①三角形的内心是___________________的交点
②三角形的内心到_____________距离相等
③三角形的内心一定在__________的内部
2、如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F,且AB=9cm，BC=14cm，CA=13cm，求AF，BD，CE的长。
3,如图，在△ABC中，点O是内心，（1）若∠ABC=50°∠ACB=75°，求∠BOC的度数。
4,已知△ABC的三边BC,AB,AC分别为a,b,c，I为内心，内切圆半径为r。求△ABC的面积。
三、归纳小结：
三角形的内切圆与外接圆的异同
四、练习：P102 第6、7题；选做P103第14题。
A
C
B
PAGE
5