北师大版四年级下小学数学《三角形内角和》教学设计
文档属性
| 名称 | 北师大版四年级下小学数学《三角形内角和》教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-15 13:40:14 | ||
图片预览


文档简介
《三角形内角和》
教学目标:
让学生经历探索过程发现三角形内角和为 180°,能运用该知识解决简单实际问题。
教学重难点:
重点:探究并理解三角形内角和是 180°,学会运用其求解三角形未知角的度数。
难点:通过有效的方法验证三角形内角和是 180°,尤其是如何引导学生在测量误差存在的情况下理解并接受这一结论。
教学过程
一、趣味导入
同学们,在数学的奇妙世界里,三角形可是非常重要的角色哦!今天老师带来了两位三角形朋友,一位是大三角形,一位是小三角形。
大三角形骄傲地说:“我的三个内角的和一定比你大!” 小三角形听了很不服气,说:“是这样吗?” 大家来猜猜看,到底谁的内角和更大呢?
我们先来回顾一下三角形的相关知识。三角形有三条边和三个角,那什么是三角形的内角呢?三角形相邻两边所夹的角就是内角。那内角和又是什么意思呢?就是这三个内角的度数加起来的总和。现在大家开动小脑筋想一想,怎么才能知道三角形的内角和是多少呢?
二、探究新知
(一)测量探究
接下来,小组活动开始啦!每个同学都准备一个三角形,我们要量一量它的每个内角的度数,然后填在小组活动记录表中。
同学们先仔细观察自己手中的三角形,看看它是什么形状的,是锐角三角形、直角三角形还是钝角三角形呢?
然后拿出量角器,认真测量每个内角的度数。测量的时候要注意量角器的中心要和角的顶点重合,0 刻度线要和角的一条边重合哦。
把测量得到的度数准确地记录下来,再计算出三个内角的和。
老师在教室里巡视,看看同学们测量和计算的情况,发现同学们都很认真呢!现在请各小组来汇报一下你们的测量结果。
小组 1:我们测量的大三角形,三个内角分别是 46°、40°、94°,内角和是 180°。
小组 2:我们的小三角形内角分别是 60°、60°、60°,内角和也是 180°。
小组 3:我们的锐角三角形内角是 69°、70°、40°,内角和是 179°。
小组 4:直角三角形内角是 90°、30°、60°,内角和 180°。
小组 5:钝角三角形内角是 120°、41°、20°,内角和 181°。
同学们,我们发现每个三角形的内角和都在 180° 左右。为什么会有一些小的偏差呢?这是因为我们在测量的时候存在误差。实际上,三角形的三个内角和都是 180° 哦!
(二)验证方法
那有没有什么方法能更准确地验证我们的想法呢?老师来给大家介绍两种方法。
撕拼法
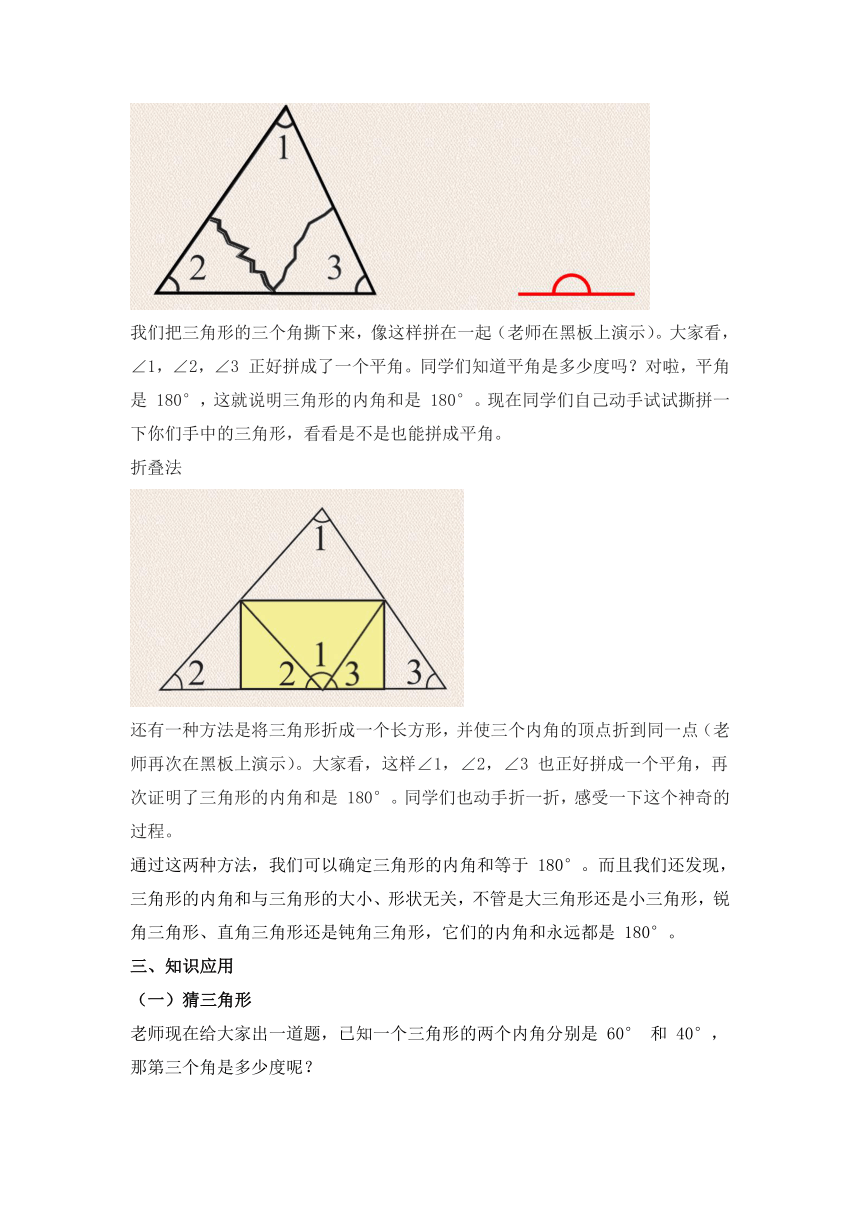
我们把三角形的三个角撕下来,像这样拼在一起(老师在黑板上演示)。大家看,∠1,∠2,∠3 正好拼成了一个平角。同学们知道平角是多少度吗?对啦,平角是 180°,这就说明三角形的内角和是 180°。现在同学们自己动手试试撕拼一下你们手中的三角形,看看是不是也能拼成平角。
折叠法
还有一种方法是将三角形折成一个长方形,并使三个内角的顶点折到同一点(老师再次在黑板上演示)。大家看,这样∠1,∠2,∠3 也正好拼成一个平角,再次证明了三角形的内角和是 180°。同学们也动手折一折,感受一下这个神奇的过程。
通过这两种方法,我们可以确定三角形的内角和等于 180°。而且我们还发现,三角形的内角和与三角形的大小、形状无关,不管是大三角形还是小三角形,锐角三角形、直角三角形还是钝角三角形,它们的内角和永远都是 180°。
三、知识应用
(一)猜三角形
老师现在给大家出一道题,已知一个三角形的两个内角分别是 60° 和 40°,那第三个角是多少度呢?
同学们算一算。对啦,根据三角形内角和是 180°,用 180 - 60 - 40 = 80°。那同学们猜猜看,这个三角形可能是什么三角形呢?
有些同学说可能是锐角三角形,因为三个角都小于 90°。有些同学说也有可能是直角三角形或者钝角三角形,因为只知道一个角是 80°,另外两个角的情况还不确定。同学们说得都很有道理,所以锐角三角形、直角三角形和钝角三角形都有可能哦!
(二)图形内角和计算
三角尺拼图
现在我们来看这道题。
用两把完全相同的三角尺分别拼出一个四边形和一个三角形。同学们想一想,它们的内角和分别是多少呢?
我们先看拼出的四边形,它的四个角都是直角,所以内角和是 90°+ 90°+90°+90°=360°。再看拼出的三角形,它的内角是 90°、45°、45°,内角和就是 90°+ 45°+ 45°=180°。同学们,你们算对了吗?现在大家再用量角器量一量,验证一下我们计算的结果。
长方形剪纸
接下来,用一张长方形纸剪一剪。我们把长方形纸沿着对角线剪成两个三角形,那这两个三角形的内角和是多少呢?对啦,都是 180°。那原来长方形的内角和是多少呢?长方形的四个角也都是直角,所以内角和是 360°。
(三)判断对错
老师这里还有一些三角形的说法,大家来判断一下它们说得对不对。
有一个三角形说:“我的两个锐角之和大于 90°。” 同学们想一想,这种说法一定对吗?其实不一定哦,如果是直角三角形,两个锐角之和就是 90°;如果是钝角三角形,两个锐角之和就小于 90°。
还有一个三角形说:“我的两个锐角之和正好等于 90°。” 这也不一定对,只有直角三角形的两个锐角之和才是 90°。
(四)求角的度数
最后,我们来填出下面各角的度数。
已知在一个三角形中,∠A = 35°,∠B = 75°,那∠C 是多少度呢?根据三角形内角和是 180°,用 180 - 35 - 75 = 70°,所以∠C = 70°。
再看另一个三角形,∠A = 28°,∠C = 64°,那∠B 是多少度呢?用 180 - 28 - 64 = 88°,所以∠B = 88°。
还有一个三角形,∠B = 55°,∠C = 115°,那∠A 是多少度呢?用 180 - 55 - 115 = 10°,所以∠A = 10°。
四、课堂总结
同学们,今天我们一起经历了一场有趣的数学探索之旅。我们通过测量、撕拼、折叠等方法,发现了三角形内角和的重要规律,那就是三角形的内角和等于 180°。而且我们还学会了根据这个规律,当已知三角形中两个内角的度数时,求出第三个内角的度数,并且可以判断三角形的形状。在这个过程中,大家都表现得非常棒!希望同学们在今后的数学学习中,继续保持这种探索精神,发现更多数学的奥秘哦!
五、课后拓展
同学们,课后请大家用不同的三角形(比如等边三角形、等腰三角形等)再次验证三角形内角和是 180°,并且尝试用多种方法向爸爸妈妈展示我们今天学到的知识。还可以找一找生活中哪些地方用到了三角形内角和的知识呢?下节课我们一起来分享。
通过这样的教学过程,学生能够在趣味中学习,逐步深入理解三角形内角和的概念和应用,培养学生的动手能力、思维能力和解决问题的能力。
教学目标:
让学生经历探索过程发现三角形内角和为 180°,能运用该知识解决简单实际问题。
教学重难点:
重点:探究并理解三角形内角和是 180°,学会运用其求解三角形未知角的度数。
难点:通过有效的方法验证三角形内角和是 180°,尤其是如何引导学生在测量误差存在的情况下理解并接受这一结论。
教学过程
一、趣味导入
同学们,在数学的奇妙世界里,三角形可是非常重要的角色哦!今天老师带来了两位三角形朋友,一位是大三角形,一位是小三角形。
大三角形骄傲地说:“我的三个内角的和一定比你大!” 小三角形听了很不服气,说:“是这样吗?” 大家来猜猜看,到底谁的内角和更大呢?
我们先来回顾一下三角形的相关知识。三角形有三条边和三个角,那什么是三角形的内角呢?三角形相邻两边所夹的角就是内角。那内角和又是什么意思呢?就是这三个内角的度数加起来的总和。现在大家开动小脑筋想一想,怎么才能知道三角形的内角和是多少呢?
二、探究新知
(一)测量探究
接下来,小组活动开始啦!每个同学都准备一个三角形,我们要量一量它的每个内角的度数,然后填在小组活动记录表中。
同学们先仔细观察自己手中的三角形,看看它是什么形状的,是锐角三角形、直角三角形还是钝角三角形呢?
然后拿出量角器,认真测量每个内角的度数。测量的时候要注意量角器的中心要和角的顶点重合,0 刻度线要和角的一条边重合哦。
把测量得到的度数准确地记录下来,再计算出三个内角的和。
老师在教室里巡视,看看同学们测量和计算的情况,发现同学们都很认真呢!现在请各小组来汇报一下你们的测量结果。
小组 1:我们测量的大三角形,三个内角分别是 46°、40°、94°,内角和是 180°。
小组 2:我们的小三角形内角分别是 60°、60°、60°,内角和也是 180°。
小组 3:我们的锐角三角形内角是 69°、70°、40°,内角和是 179°。
小组 4:直角三角形内角是 90°、30°、60°,内角和 180°。
小组 5:钝角三角形内角是 120°、41°、20°,内角和 181°。
同学们,我们发现每个三角形的内角和都在 180° 左右。为什么会有一些小的偏差呢?这是因为我们在测量的时候存在误差。实际上,三角形的三个内角和都是 180° 哦!
(二)验证方法
那有没有什么方法能更准确地验证我们的想法呢?老师来给大家介绍两种方法。
撕拼法
我们把三角形的三个角撕下来,像这样拼在一起(老师在黑板上演示)。大家看,∠1,∠2,∠3 正好拼成了一个平角。同学们知道平角是多少度吗?对啦,平角是 180°,这就说明三角形的内角和是 180°。现在同学们自己动手试试撕拼一下你们手中的三角形,看看是不是也能拼成平角。
折叠法
还有一种方法是将三角形折成一个长方形,并使三个内角的顶点折到同一点(老师再次在黑板上演示)。大家看,这样∠1,∠2,∠3 也正好拼成一个平角,再次证明了三角形的内角和是 180°。同学们也动手折一折,感受一下这个神奇的过程。
通过这两种方法,我们可以确定三角形的内角和等于 180°。而且我们还发现,三角形的内角和与三角形的大小、形状无关,不管是大三角形还是小三角形,锐角三角形、直角三角形还是钝角三角形,它们的内角和永远都是 180°。
三、知识应用
(一)猜三角形
老师现在给大家出一道题,已知一个三角形的两个内角分别是 60° 和 40°,那第三个角是多少度呢?
同学们算一算。对啦,根据三角形内角和是 180°,用 180 - 60 - 40 = 80°。那同学们猜猜看,这个三角形可能是什么三角形呢?
有些同学说可能是锐角三角形,因为三个角都小于 90°。有些同学说也有可能是直角三角形或者钝角三角形,因为只知道一个角是 80°,另外两个角的情况还不确定。同学们说得都很有道理,所以锐角三角形、直角三角形和钝角三角形都有可能哦!
(二)图形内角和计算
三角尺拼图
现在我们来看这道题。
用两把完全相同的三角尺分别拼出一个四边形和一个三角形。同学们想一想,它们的内角和分别是多少呢?
我们先看拼出的四边形,它的四个角都是直角,所以内角和是 90°+ 90°+90°+90°=360°。再看拼出的三角形,它的内角是 90°、45°、45°,内角和就是 90°+ 45°+ 45°=180°。同学们,你们算对了吗?现在大家再用量角器量一量,验证一下我们计算的结果。
长方形剪纸
接下来,用一张长方形纸剪一剪。我们把长方形纸沿着对角线剪成两个三角形,那这两个三角形的内角和是多少呢?对啦,都是 180°。那原来长方形的内角和是多少呢?长方形的四个角也都是直角,所以内角和是 360°。
(三)判断对错
老师这里还有一些三角形的说法,大家来判断一下它们说得对不对。
有一个三角形说:“我的两个锐角之和大于 90°。” 同学们想一想,这种说法一定对吗?其实不一定哦,如果是直角三角形,两个锐角之和就是 90°;如果是钝角三角形,两个锐角之和就小于 90°。
还有一个三角形说:“我的两个锐角之和正好等于 90°。” 这也不一定对,只有直角三角形的两个锐角之和才是 90°。
(四)求角的度数
最后,我们来填出下面各角的度数。
已知在一个三角形中,∠A = 35°,∠B = 75°,那∠C 是多少度呢?根据三角形内角和是 180°,用 180 - 35 - 75 = 70°,所以∠C = 70°。
再看另一个三角形,∠A = 28°,∠C = 64°,那∠B 是多少度呢?用 180 - 28 - 64 = 88°,所以∠B = 88°。
还有一个三角形,∠B = 55°,∠C = 115°,那∠A 是多少度呢?用 180 - 55 - 115 = 10°,所以∠A = 10°。
四、课堂总结
同学们,今天我们一起经历了一场有趣的数学探索之旅。我们通过测量、撕拼、折叠等方法,发现了三角形内角和的重要规律,那就是三角形的内角和等于 180°。而且我们还学会了根据这个规律,当已知三角形中两个内角的度数时,求出第三个内角的度数,并且可以判断三角形的形状。在这个过程中,大家都表现得非常棒!希望同学们在今后的数学学习中,继续保持这种探索精神,发现更多数学的奥秘哦!
五、课后拓展
同学们,课后请大家用不同的三角形(比如等边三角形、等腰三角形等)再次验证三角形内角和是 180°,并且尝试用多种方法向爸爸妈妈展示我们今天学到的知识。还可以找一找生活中哪些地方用到了三角形内角和的知识呢?下节课我们一起来分享。
通过这样的教学过程,学生能够在趣味中学习,逐步深入理解三角形内角和的概念和应用,培养学生的动手能力、思维能力和解决问题的能力。
