1.4整式的乘法 课件 (1)

课件29张PPT。1.4整式的乘法（三）北师大版数学七年级下
第一章 整式的运算-----多项式乘以多项式再把所得的积相加。如何进行单项式与多项式乘法的运算？用单项式去乘多项式的每一项，单项式乘以多项式的依据是
; 乘法分配律.进行单项式与多项式乘法运算
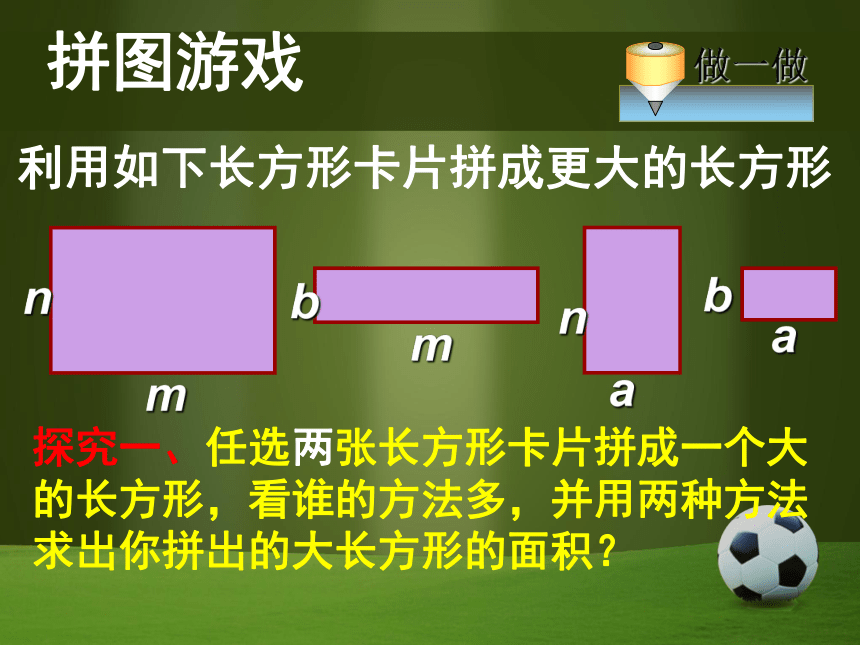
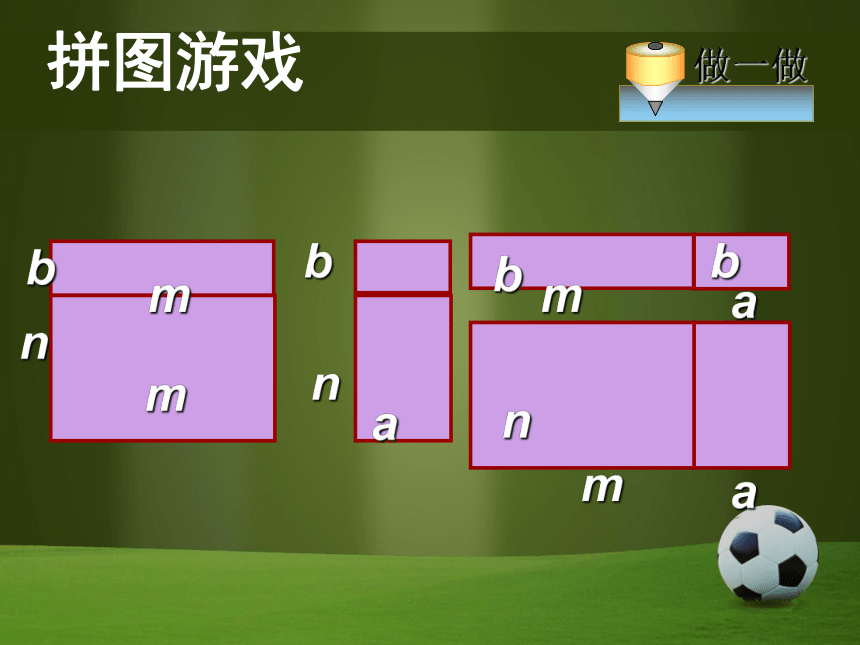
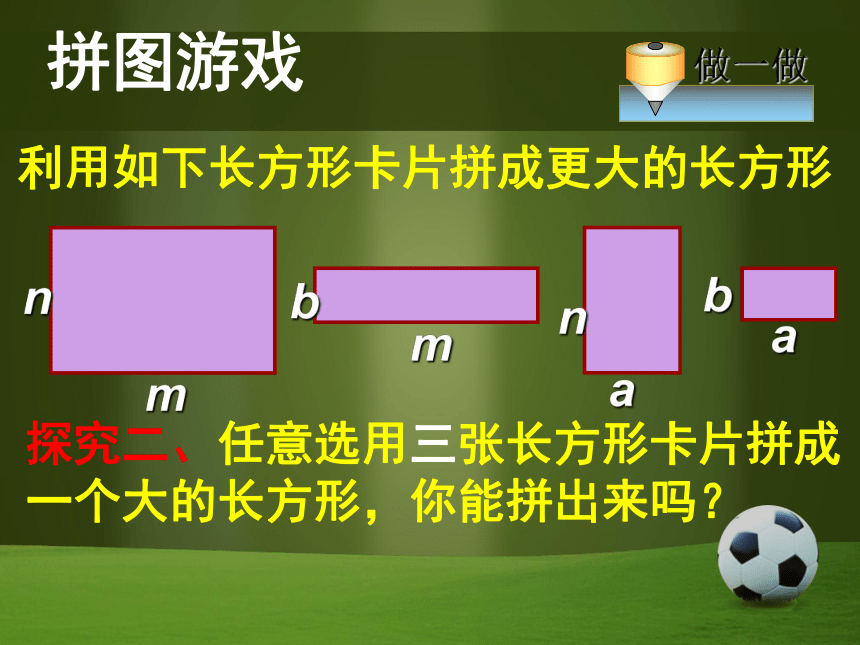
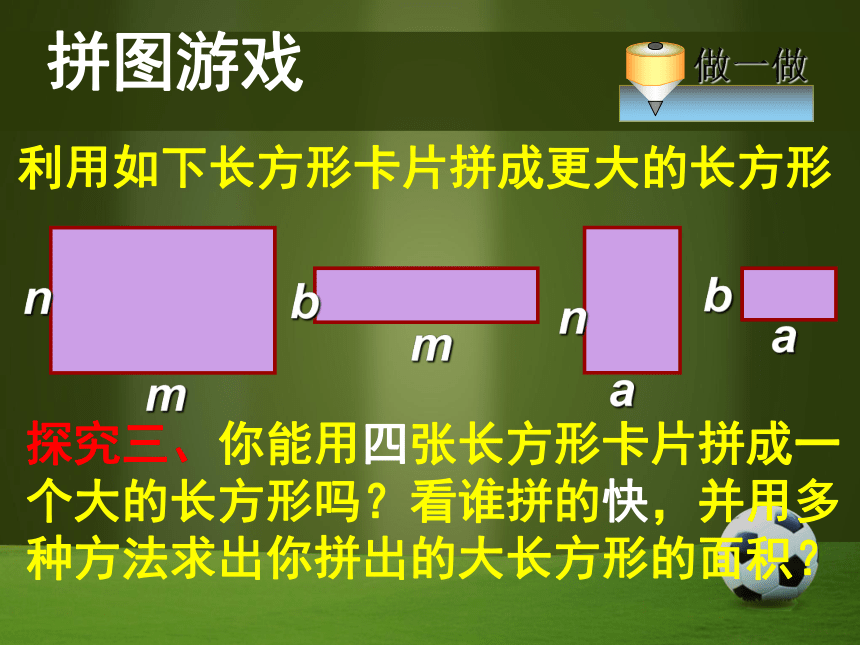
时，要注意一些什么?① 不能漏乘:即单项式要乘遍多项式的每一项② 注意符号的确定.前置诊断计算：(1)（3mn)2(m2+mn-n2)(2)2a2-a(2a-5b) (2)5ab答案：(1)9m4n2－9m2n4 +9m3n3 拼图游戏利用如下长方形卡片拼成更大的长方形mnmabnba探究一、任选两张长方形卡片拼成一个大的长方形，看谁的方法多，并用两种方法求出你拼出的大长方形的面积？拼图游戏mnmabnbamanmabb拼图游戏利用如下长方形卡片拼成更大的长方形mnmabnba探究二、任意选用三张长方形卡片拼成一个大的长方形，你能拼出来吗？
拼图游戏mnmabnba
mnaba
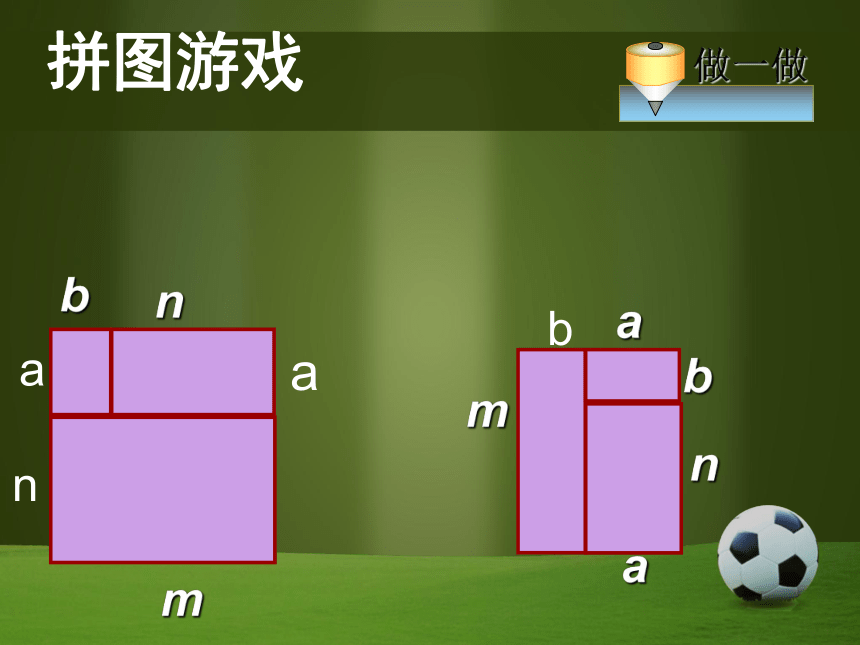
拼图游戏利用如下长方形卡片拼成更大的长方形mnmabnba探究三、你能用四张长方形卡片拼成一个大的长方形吗？看谁拼的快，并用多种方法求出你拼出的大长方形的面积？
bnm用不同的形式表示所拼长方形的面积(１)用长方形的面积法，
理解多项式乘多项式的公式展开。(m+a)(n+b)mn+mb+an+ab=mbn(m+a)(n+b)= mn+mb+an+ab 的理解将等号两端的 x 换成(n+b)则有： 在 (m+a)x = mx + ax 中，(m+a) x =m x +a x(n+b)(n+b)(n+b)(2)用单项式乘多项式理解公式展开=mn+mb + an+ab(m+a)(n+b)=mn1234这个结果还可以从下面的图中反映出来多项式的乘法+mb+an+ab(3)用连线法理解公式：mn+ mb+ ab+ an学会连一连：(a+b)(c+d)=ac+bc+bd+ad-by(a+b)(x–y)=ax+bx-ay学会连一连： 如何记忆多项式与多项式相乘的运算法则： 先用一个多项式的每一项
乘另一个多项式的每一项再把所得的积相加。(m+a)(n+b)=mn+ mb+ an+ ab比一比看谁做的又快又对：(a+b+c)(d+e+f)=考考你ad+ae+af+bd+be+bf+cd+ce+cf例题解析例题解析【例3】计算： (1)(1?x)(0.6?x)；?x?0.6 ? x +=0.6?1.6x+x2 x? x=0.6最后的结果要合并同类项. 两项相乘时,先定符号例题解析例题解析【例3】计算： (2)(2x + y)(x?y)。（2） (2x + y)(x?y)=2xx2x?x2x?y?2x? y+ y+ y?x+??y?y=2x2?2xy+ xy?y2=2x2 ?xy?y2p19(1)(m+2n)(m-2n) (2)(2n +5)(n?3) ;1、计算：(3)(x+2y)2 ; (4)(ax+b)(cx+d ) .答案:（1）m2-4n2(2)2n2-n-15(3)x2+4xy+4y2(4)acx2+adx+bcx+bd注意 !1.计算(x+2y)2应该这样做(x+2y)2 =(x+2y)(x+2y)
=x2+2xy+2xy+4y2
=x2+4xy+4y2
切记: 一般情况下
(x+2y)2不等于x2+4y2 .练习一、计算：(2) (2x+3)(3x–1);(3)(2x+5)(2x+5).(1) (2n+6)(n–3);练习二、计算：(1) (2a–3b)(a+5b) ;(2) (3a–2)(a–1)–(a+1)(a+2) ;注 意 !2.(3a–2)(a–1)–(a+1)(a+2)
是多项式的积与积的差，后两个多项式乘积的展开式要用括号括起来。
先用一个多项式的每一项
乘另一个多项式的每一项再把所得的积相加。小结本节课你学到了什么?多项式乘多项式的乘法法则：运用多项式乘法法则要注意： (4)最后的计算结果要化简￣￣￣合并同类项． 作业P19 习题 1.8知识技能：第1题 再见