三角形全等专题复习课件

课件14张PPT。探索三角形全等的条件
专题复习 学习目标1.通过本节课的学习，我们将更进一步明白三角形全等的判定方法。
2.我们能灵活运用“SSS”、“SAS”、“ASA”、“AAS” 来判定三角形全等。
3.会用三角形全等的条件推理和论证有关问题。
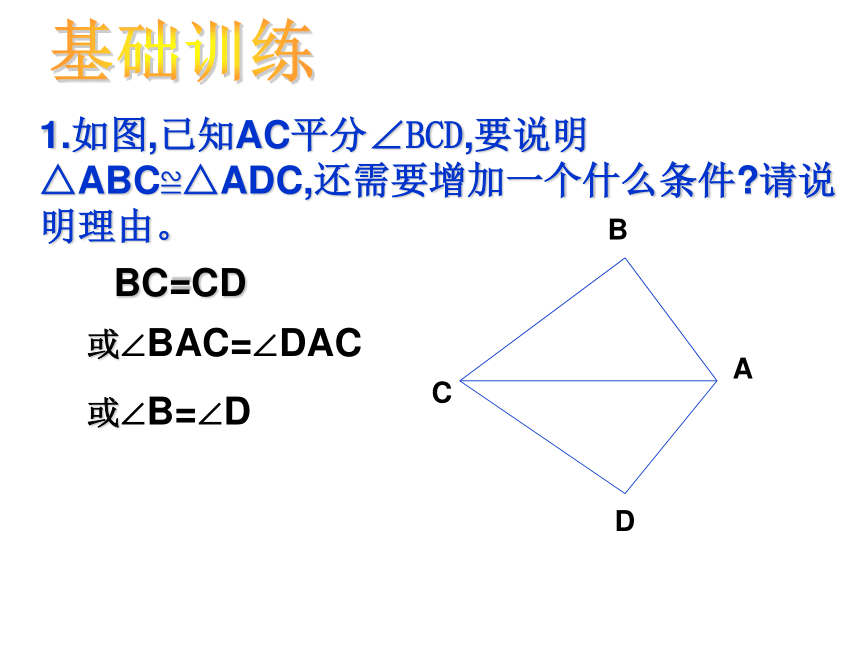
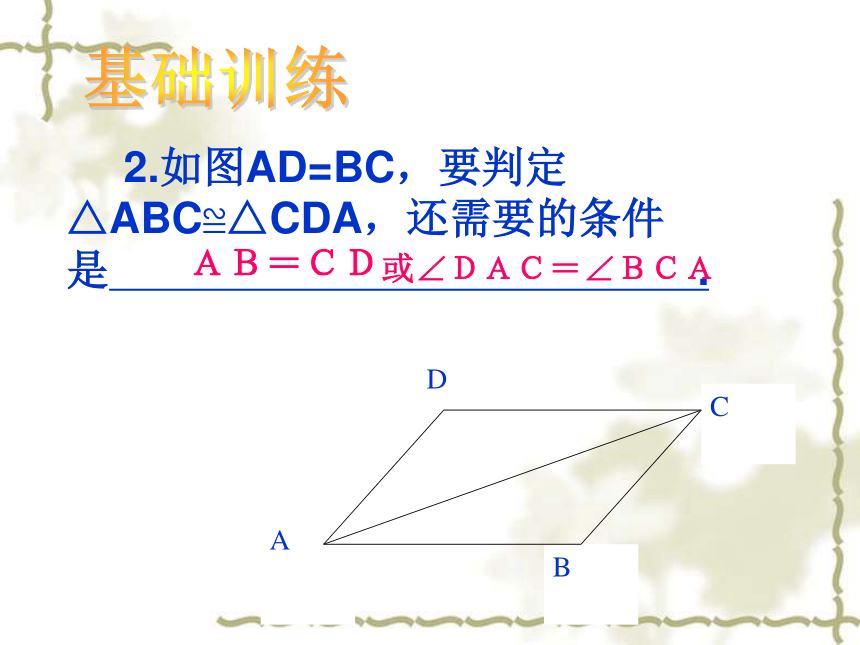
4.通过学习，我们的思维会越来越灵活。三角形全等的判定方法（1）全等三角形的定义（2）边边边公理（SSS）（3）边角边公理（SAS）三边对应相等的两个三角形全等两边及它们的夹角对应相等的两个三角形全等能够完全重合的两个三角形是全等三角形（4）角边角公理（ASA）两角及它们的夹边对应相等的两个三角形全等（5）角角边公理（AAS）两角及其中一角的对边对应相等的两个三角形全等概念导引1.如图,已知AC平分∠BCD,要说明△ABC≌△ADC,还需要增加一个什么条件?请说明理由。或∠BAC=∠DACBC=CD或∠B=∠D基础训练2.如图AD=BC，要判定 △ABC≌△CDA，还需要的条件是 　　 .
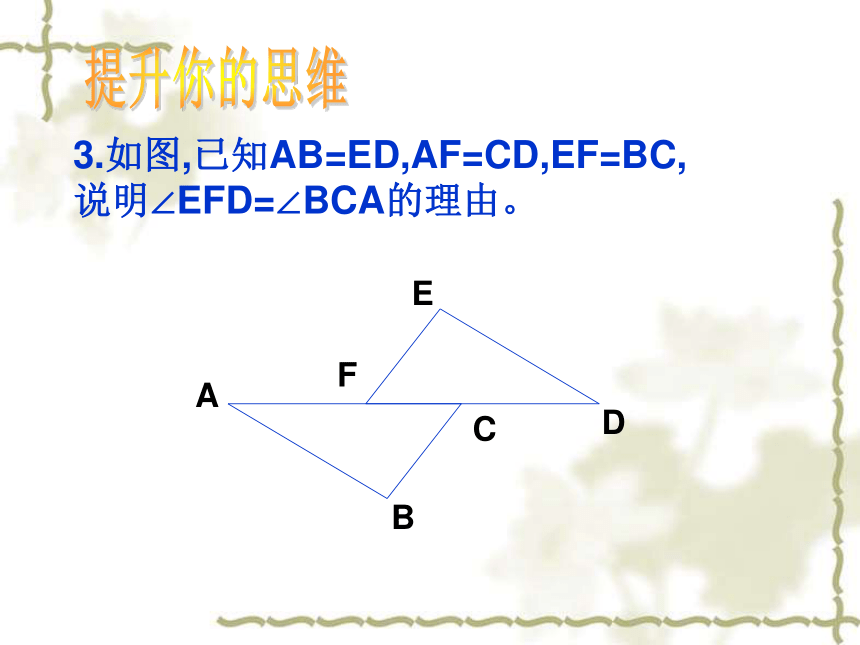
基础训练ＡＢ＝ＣＤ或∠ＤＡＣ＝∠ＢＣＡBAFCDE3.如图,已知AB=ED,AF=CD,EF=BC,
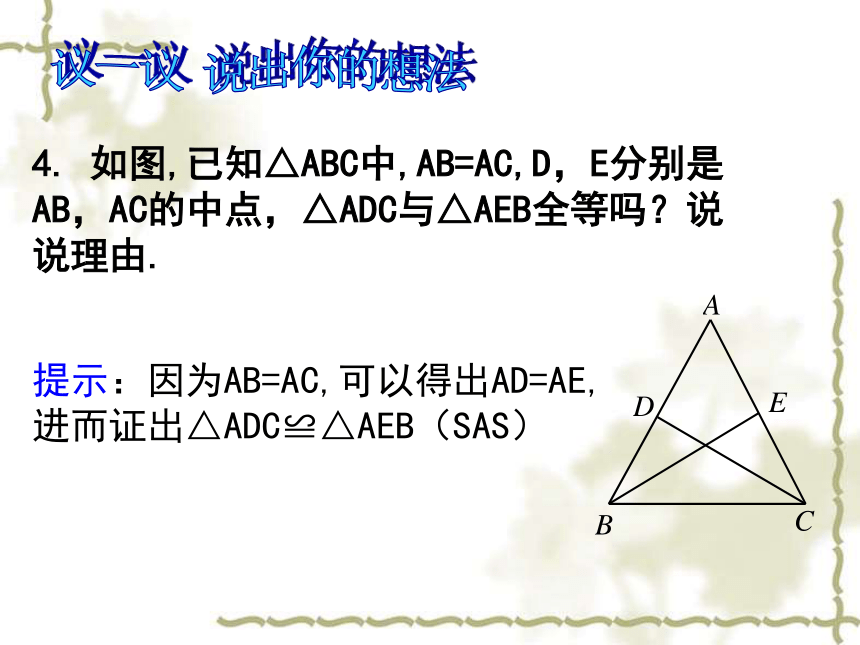
说明∠EFD=∠BCA的理由。提升你的思维4. 如图,已知△ABC中,AB=AC,D，E分别是AB，AC的中点，△ADC与△AEB全等吗？说说理由. 提示：因为AB=AC,可以得出AD=AE,
进而证出△ADC≌△AEB（SAS）. 议一议 说出你的想法5.如图，BE=CD，∠1=∠2，则AB=AC吗？为什么？讲 解争先恐后哦如图，BE=CD，∠1=∠2，则AB=AC吗？为什么？解:∵∠1=∠2（ ）已知∴∠ADC=∠AEB（ ）等角的补角相等在△ADC和△AEB中∠A=∠A（ ）公共角∠ADC=∠AEB（ ）已证DC=EB（ ）已知 ∴△ADC≌△AEB（ ）AAS∴AB=AC（ ）全等三角形的对应边相等6.如图:AC和DB相交于点O,若AB=DC，AC=DB，则∠B=∠C,请说明理由.小组讨论题：如图:AC和DB相交于点O,若AB=DC，AC=DB，则∠B=∠C,请说明理由.如图，∠1=∠2，AB=CD，AC与BD相交于点O，则图中必定全等的三角形有（ ）
A. 2对 B. 3对
C. 4对 D. 6对C你敢挑战吗中考链接课堂小结交流本节课的收获，说说存在的困惑再见祝你进步