浙江省金华市婺城区2024-2025学年九年级上学期期末数学试卷(含答案)
文档属性
| 名称 | 浙江省金华市婺城区2024-2025学年九年级上学期期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 277.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-15 22:41:47 | ||
图片预览



文档简介
2024 学年第一学期九年级期末检测 数学试题卷
考生须知:
1. 全卷共三大题, 24 小题, 全卷满分 120 分, 考试时间 120 分钟。
2. 全卷分试卷 I (选择题) 和试卷 II (非选择题) 两部分, 全部在答题卷上作答, 卷 I 的答案必须用 铅笔填涂;卷II的答案必须用黑色字迹钢笔或签字笔答在答题卷的相应位置上。
卷 I
一、选择题 (本大题有 10 小题, 每小题 3 分, 共 30 分。请选出各题中一个符合题意的正确选项, 不选、多选、错选均不给分)
1. 若 ,则 的值是 ( )
A. 2 B. 3 C. D.
2. 已知 的半径为 。若点 在 外,则 的长可能是 ( )
A. B. C. D.
3. 一副除去大小王的扑克牌中,抽取一张扑克牌恰好是“红桃”这一事件是( )
A. 随机事件 B. 不可能事件 C. 必然事件 D. 确定性事件
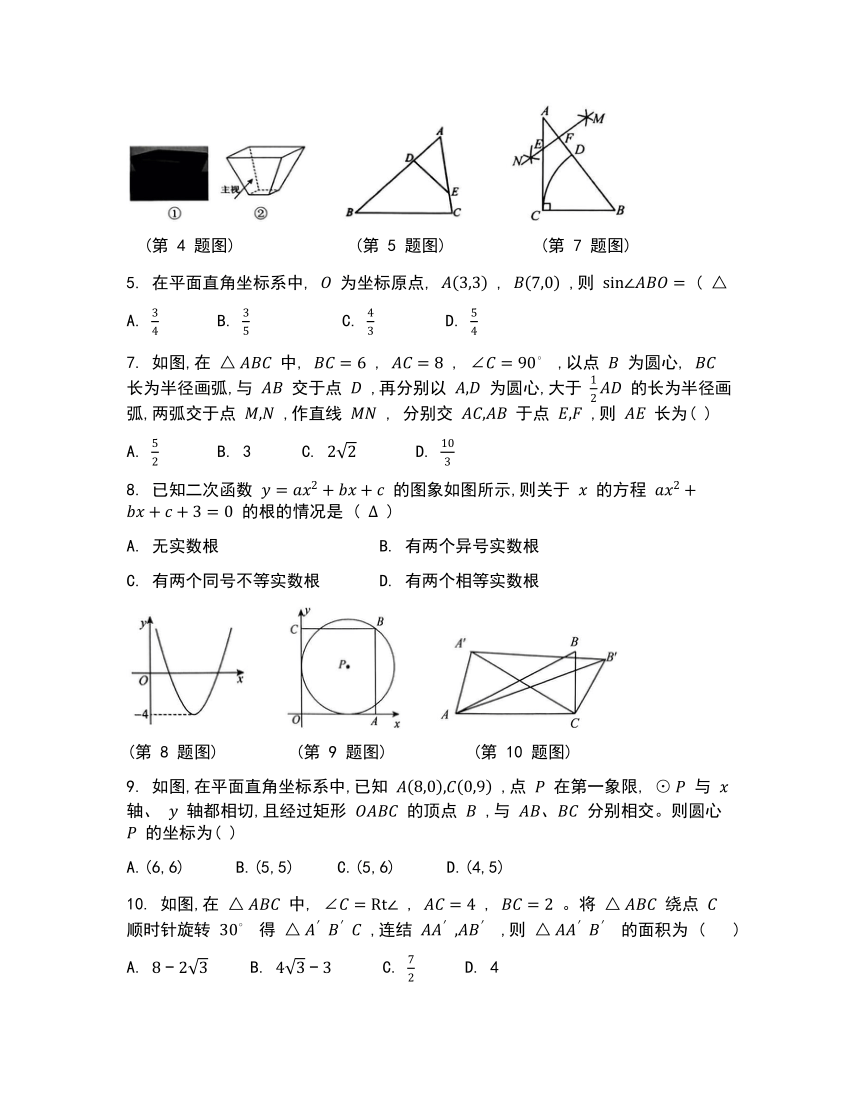
4. 图①是古代必备的粮食度量用具叫“斗”,图②是它的示意图,则该 “斗” 的三视图中图形相同的是( ▲ )
A. 主视图与俯视图 B. 左视图与主视图
C. 左视图与俯视图 D. 左视图、主视图、俯视图均相同
5. 如图, , , ,则 等于( )
A. B. C. D.
(第 4 题图) (第 5 题图) (第 7 题图)
5. 在平面直角坐标系中, 为坐标原点, , ,则 (
A. B. C. D.
7. 如图,在 中, , , ,以点 为圆心, 长为半径画弧,与 交于点 ,再分别以 为圆心,大于 的长为半径画弧,两弧交于点 ,作直线 , 分别交 于点 ,则 长为( )
A. B. 3 C. D.
8. 已知二次函数 的图象如图所示,则关于 的方程 的根的情况是 ( )
A. 无实数根 B. 有两个异号实数根
C. 有两个同号不等实数根 D. 有两个相等实数根
(第 8 题图) (第 9 题图) (第 10 题图)
9. 如图,在平面直角坐标系中,已知 ,点 在第一象限, 与 轴、 轴都相切,且经过矩形 的顶点 ,与 分别相交。则圆心 的坐标为( )
A.(6,6) B.(5,5) C.(5,6) D.(4,5)
10. 如图,在 中, , , 。将 绕点 顺时针旋转 得 ,连结 ,则 的面积为 ( )
A. B. C. D. 4
卷 II
二、填空题 (本大题有 6 小题, 每小题 3 分, 共 18 分。)
11. 抛物线 的顶点坐标是_____▲_____。
12. 在一个不透明的袋子中有红球和白球共 20 个, 它们除颜色外都相同, 每次从袋中随机摸出一个小球, 记下颜色后再放回袋中, 通过多次重复实验, 发现摸出白球的频率稳定在 0.7 附近, 则估计袋子中的白球有_____▲_____个。
13. 如图,将直角三角板的锐角顶点 放在 上,边 与 分别交于点 ,连结 。 若 , ,则 的半径为_____▲_____cm。
(第 13 题图) (第 14 题图) (第 15 题图) (第 16 题图)
14. 如图,地面 上的点 处放置平面镜,光线从 点射出经平面镜 (点 处) 反射后照射到 点。已知 ,垂足分别为 米, 米, 米,则 长为_____▲_____米。
15. 如图, 与正八边形 相切于点 ,若 的半径为 8,则 的长为_____▲_____ (结果保留 )。
16. 如图,在菱形 中, ,点 在 上,以 为边作菱形 ,使点 在 的延长线上,连结 , ,延长 交 于点 。若 是 的中点,则 _____▲_____。
三、解答题 (本大题有 8 小题, 共 72 分。)
17. (本题 6 分) 计算: 。
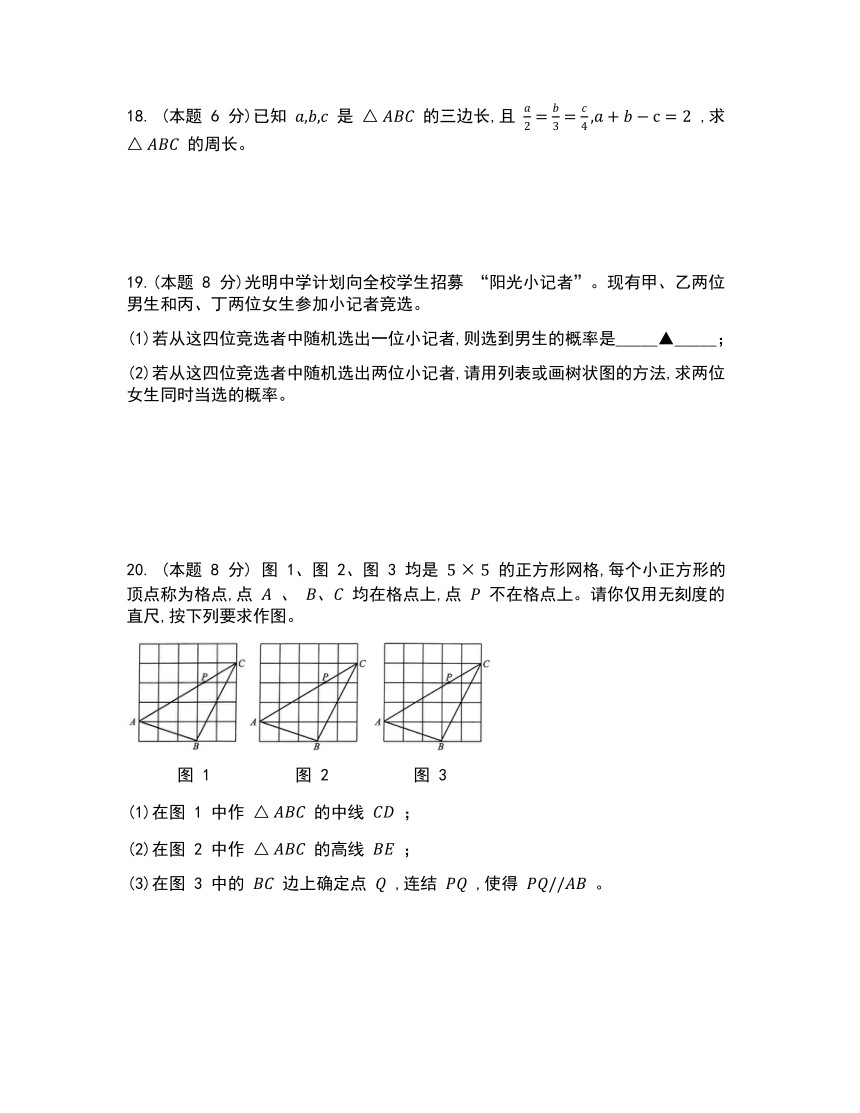
(本题 6 分)已知 是 的三边长,且 ,求 的周长。
19.(本题 8 分)光明中学计划向全校学生招募 “阳光小记者”。现有甲、乙两位男生和丙、丁两位女生参加小记者竞选。
(1)若从这四位竞选者中随机选出一位小记者,则选到男生的概率是_____▲_____;
(2)若从这四位竞选者中随机选出两位小记者,请用列表或画树状图的方法,求两位女生同时当选的概率。
20. (本题 8 分) 图 1、图 2、图 3 均是 的正方形网格,每个小正方形的顶点称为格点,点 、 均在格点上,点 不在格点上。请你仅用无刻度的直尺,按下列要求作图。
图 1 图 2 图 3
(1)在图 1 中作 的中线 ;
(2)在图 2 中作 的高线 ;
(3)在图 3 中的 边上确定点 ,连结 ,使得 。
21. (本题 8 分) 对于一个任意的四位数 ,若 的千位数字与个位数字之和等于百位数字与十位数字之和,我们称这样的四位数为 “稳定数”。例如: 四位数 3197,因为 ,所以四位数 3197 是稳定数。
(1)填空:2025_____ 稳定数(填 “是” 或 “不是”);
(2)已知一个稳定数的千位数字为 1 ,百位数字为 9 ,求这个稳定数;
(3)命题 “两个稳定数的和仍是稳定数” 是真命题还是假命题?请说明理由。
22.(本题 10 分)汽车盲区是指驾驶员位于驾驶座位置,其视线被车体遮挡而不能直接观察到的区域。如图, 、 分别为汽车两侧盲区的示意图,已知视线 与地面 的夹角 ,视线 与地面 的夹角 ,点 分别为 与车窗底部的交点, , , 垂直地面 , 点到 点的距离 。(参考数据: ,
(1)求车窗底部到地面的高度(即 的长);
(2)求盲区中 的长度;
(3)点 在 上, ,在 处有一个高度为 的物体,驾驶员能观察到物体吗? 请说明理由。
23. (本题 12 分) 已知在同一平面直角坐标系内的两条抛物线 ( 为常数)。
(1)若抛物线 与 轴正半轴的交点落在抛物线 上,求 的值;
( 2 )已知抛物线 可由抛物线 绕点 旋转 得到,求点 的坐标;
若在 的范围内,始终存在 ,求 的取值范围(直接写出答案)。
24. (本题 12 分) 如图 1,在 中, ,以 为直径的 交 分别于点 , ,连结 相交于点 ,连结 。
(1)求证: ;
(2)若 ,求 的值;
(3)过点 作 于点 ,交于 于点 ,交 于点 (如图 2)。
求证: 。
图 1 图 2
2024 学年第一学期九年级期末检测 数学参考答案及评分细则
一、选择题 (本题共 10 小题, 每小题 3 分, 共 30 分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A B D B A C B A
评分标准 选对一题给 3 分,不选,多选,错选均不给分
二、填空题 (本题有 6 小题, 每小题 3 分,共 18 分)
11.(0, - 2); 12. 14 ; 15. 6 16. 。
三、解答题 (本题有 8 小题, 共 72 分. )
17. (本题 6 分)
原式 .4 分
.2 分
18. (本题 6 分)
设 ,则 .2 分
,解得 .2 分
的周长为 .2 分
19. (本题 8 分)
(1) .3 分
(2)根据题意,画出树状图,如下: 第一名: .3 分第二名: 两位女生同时当选的概率是 .2 分
20. (本题 8 分)
作图略,各小题作图方案都不唯一,正确即可。
第(1)小题 3 分;第(2)小题 3 分;第(3)小题 2 分
21. (本题 10 分)
(1)不是 .3 分
(2)设十位数字为 ,个位数字为 ,根据题意,得
所求的稳定数为 1980 或 1919。 .4 分
(3)是假命题,反例如下: .1 分
四位数 2817 与 2222 都是稳定数,它们的和等于 5039
然而四位数 5039 不是稳定数
两个稳定数的和仍是稳定数”是假命题 2 分
22. (本题 10 分)
(1) 在 中,
.3 分
答:车窗底部到地面的高度为 1.12 米
(2)由题意:四边形 是矩形
,
在 Rt 中,
,
答: 盲区中 的长度为 .3 分
(3)过点 作 ,
,
由 MNIIFD,得 ,
故 ,即 ,
解得: ,
在 处有一个高度为 的物体,驾驶员能观察到物体。 .4 分
23. (本题 12 分)
(1)把 代入 ,得 ,解得
抛物线 与 轴正半轴的交点为(2,0) .2 分
把(2,0)代入 ,得 解得 .2 分
(2)由题意:抛物线 与抛物线 关于点 成中心对称
抛物线 与抛物线 开口大小相同,开口方向相反
.2 分
抛物线 顶点坐标为 ,抛物线 的顶点坐标为(0, - 4)
点 坐标为 .2 分
(3) (求得临界值各得 1 分) 4 分
24. (本题 12 分)
图 1
(1)证明略 .4 分
(2)由 得 , ,则
图 2
,即 .4 分
(3)简略思路:
方法 1: 连结 ,可证明
由 ,得
由 ,得
即
图 2
方法 2: 连结 ,可证明
由 ,得
即 .4 分
考生须知:
1. 全卷共三大题, 24 小题, 全卷满分 120 分, 考试时间 120 分钟。
2. 全卷分试卷 I (选择题) 和试卷 II (非选择题) 两部分, 全部在答题卷上作答, 卷 I 的答案必须用 铅笔填涂;卷II的答案必须用黑色字迹钢笔或签字笔答在答题卷的相应位置上。
卷 I
一、选择题 (本大题有 10 小题, 每小题 3 分, 共 30 分。请选出各题中一个符合题意的正确选项, 不选、多选、错选均不给分)
1. 若 ,则 的值是 ( )
A. 2 B. 3 C. D.
2. 已知 的半径为 。若点 在 外,则 的长可能是 ( )
A. B. C. D.
3. 一副除去大小王的扑克牌中,抽取一张扑克牌恰好是“红桃”这一事件是( )
A. 随机事件 B. 不可能事件 C. 必然事件 D. 确定性事件
4. 图①是古代必备的粮食度量用具叫“斗”,图②是它的示意图,则该 “斗” 的三视图中图形相同的是( ▲ )
A. 主视图与俯视图 B. 左视图与主视图
C. 左视图与俯视图 D. 左视图、主视图、俯视图均相同
5. 如图, , , ,则 等于( )
A. B. C. D.
(第 4 题图) (第 5 题图) (第 7 题图)
5. 在平面直角坐标系中, 为坐标原点, , ,则 (
A. B. C. D.
7. 如图,在 中, , , ,以点 为圆心, 长为半径画弧,与 交于点 ,再分别以 为圆心,大于 的长为半径画弧,两弧交于点 ,作直线 , 分别交 于点 ,则 长为( )
A. B. 3 C. D.
8. 已知二次函数 的图象如图所示,则关于 的方程 的根的情况是 ( )
A. 无实数根 B. 有两个异号实数根
C. 有两个同号不等实数根 D. 有两个相等实数根
(第 8 题图) (第 9 题图) (第 10 题图)
9. 如图,在平面直角坐标系中,已知 ,点 在第一象限, 与 轴、 轴都相切,且经过矩形 的顶点 ,与 分别相交。则圆心 的坐标为( )
A.(6,6) B.(5,5) C.(5,6) D.(4,5)
10. 如图,在 中, , , 。将 绕点 顺时针旋转 得 ,连结 ,则 的面积为 ( )
A. B. C. D. 4
卷 II
二、填空题 (本大题有 6 小题, 每小题 3 分, 共 18 分。)
11. 抛物线 的顶点坐标是_____▲_____。
12. 在一个不透明的袋子中有红球和白球共 20 个, 它们除颜色外都相同, 每次从袋中随机摸出一个小球, 记下颜色后再放回袋中, 通过多次重复实验, 发现摸出白球的频率稳定在 0.7 附近, 则估计袋子中的白球有_____▲_____个。
13. 如图,将直角三角板的锐角顶点 放在 上,边 与 分别交于点 ,连结 。 若 , ,则 的半径为_____▲_____cm。
(第 13 题图) (第 14 题图) (第 15 题图) (第 16 题图)
14. 如图,地面 上的点 处放置平面镜,光线从 点射出经平面镜 (点 处) 反射后照射到 点。已知 ,垂足分别为 米, 米, 米,则 长为_____▲_____米。
15. 如图, 与正八边形 相切于点 ,若 的半径为 8,则 的长为_____▲_____ (结果保留 )。
16. 如图,在菱形 中, ,点 在 上,以 为边作菱形 ,使点 在 的延长线上,连结 , ,延长 交 于点 。若 是 的中点,则 _____▲_____。
三、解答题 (本大题有 8 小题, 共 72 分。)
17. (本题 6 分) 计算: 。
(本题 6 分)已知 是 的三边长,且 ,求 的周长。
19.(本题 8 分)光明中学计划向全校学生招募 “阳光小记者”。现有甲、乙两位男生和丙、丁两位女生参加小记者竞选。
(1)若从这四位竞选者中随机选出一位小记者,则选到男生的概率是_____▲_____;
(2)若从这四位竞选者中随机选出两位小记者,请用列表或画树状图的方法,求两位女生同时当选的概率。
20. (本题 8 分) 图 1、图 2、图 3 均是 的正方形网格,每个小正方形的顶点称为格点,点 、 均在格点上,点 不在格点上。请你仅用无刻度的直尺,按下列要求作图。
图 1 图 2 图 3
(1)在图 1 中作 的中线 ;
(2)在图 2 中作 的高线 ;
(3)在图 3 中的 边上确定点 ,连结 ,使得 。
21. (本题 8 分) 对于一个任意的四位数 ,若 的千位数字与个位数字之和等于百位数字与十位数字之和,我们称这样的四位数为 “稳定数”。例如: 四位数 3197,因为 ,所以四位数 3197 是稳定数。
(1)填空:2025_____ 稳定数(填 “是” 或 “不是”);
(2)已知一个稳定数的千位数字为 1 ,百位数字为 9 ,求这个稳定数;
(3)命题 “两个稳定数的和仍是稳定数” 是真命题还是假命题?请说明理由。
22.(本题 10 分)汽车盲区是指驾驶员位于驾驶座位置,其视线被车体遮挡而不能直接观察到的区域。如图, 、 分别为汽车两侧盲区的示意图,已知视线 与地面 的夹角 ,视线 与地面 的夹角 ,点 分别为 与车窗底部的交点, , , 垂直地面 , 点到 点的距离 。(参考数据: ,
(1)求车窗底部到地面的高度(即 的长);
(2)求盲区中 的长度;
(3)点 在 上, ,在 处有一个高度为 的物体,驾驶员能观察到物体吗? 请说明理由。
23. (本题 12 分) 已知在同一平面直角坐标系内的两条抛物线 ( 为常数)。
(1)若抛物线 与 轴正半轴的交点落在抛物线 上,求 的值;
( 2 )已知抛物线 可由抛物线 绕点 旋转 得到,求点 的坐标;
若在 的范围内,始终存在 ,求 的取值范围(直接写出答案)。
24. (本题 12 分) 如图 1,在 中, ,以 为直径的 交 分别于点 , ,连结 相交于点 ,连结 。
(1)求证: ;
(2)若 ,求 的值;
(3)过点 作 于点 ,交于 于点 ,交 于点 (如图 2)。
求证: 。
图 1 图 2
2024 学年第一学期九年级期末检测 数学参考答案及评分细则
一、选择题 (本题共 10 小题, 每小题 3 分, 共 30 分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A B D B A C B A
评分标准 选对一题给 3 分,不选,多选,错选均不给分
二、填空题 (本题有 6 小题, 每小题 3 分,共 18 分)
11.(0, - 2); 12. 14 ; 15. 6 16. 。
三、解答题 (本题有 8 小题, 共 72 分. )
17. (本题 6 分)
原式 .4 分
.2 分
18. (本题 6 分)
设 ,则 .2 分
,解得 .2 分
的周长为 .2 分
19. (本题 8 分)
(1) .3 分
(2)根据题意,画出树状图,如下: 第一名: .3 分第二名: 两位女生同时当选的概率是 .2 分
20. (本题 8 分)
作图略,各小题作图方案都不唯一,正确即可。
第(1)小题 3 分;第(2)小题 3 分;第(3)小题 2 分
21. (本题 10 分)
(1)不是 .3 分
(2)设十位数字为 ,个位数字为 ,根据题意,得
所求的稳定数为 1980 或 1919。 .4 分
(3)是假命题,反例如下: .1 分
四位数 2817 与 2222 都是稳定数,它们的和等于 5039
然而四位数 5039 不是稳定数
两个稳定数的和仍是稳定数”是假命题 2 分
22. (本题 10 分)
(1) 在 中,
.3 分
答:车窗底部到地面的高度为 1.12 米
(2)由题意:四边形 是矩形
,
在 Rt 中,
,
答: 盲区中 的长度为 .3 分
(3)过点 作 ,
,
由 MNIIFD,得 ,
故 ,即 ,
解得: ,
在 处有一个高度为 的物体,驾驶员能观察到物体。 .4 分
23. (本题 12 分)
(1)把 代入 ,得 ,解得
抛物线 与 轴正半轴的交点为(2,0) .2 分
把(2,0)代入 ,得 解得 .2 分
(2)由题意:抛物线 与抛物线 关于点 成中心对称
抛物线 与抛物线 开口大小相同,开口方向相反
.2 分
抛物线 顶点坐标为 ,抛物线 的顶点坐标为(0, - 4)
点 坐标为 .2 分
(3) (求得临界值各得 1 分) 4 分
24. (本题 12 分)
图 1
(1)证明略 .4 分
(2)由 得 , ,则
图 2
,即 .4 分
(3)简略思路:
方法 1: 连结 ,可证明
由 ,得
由 ,得
即
图 2
方法 2: 连结 ,可证明
由 ,得
即 .4 分
同课章节目录
