河南省信阳市光山县2024-2025学年八年级上学期1月期末考试数学试题(图片版,含答案)
文档属性
| 名称 | 河南省信阳市光山县2024-2025学年八年级上学期1月期末考试数学试题(图片版,含答案) |  | |
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 22:48:50 | ||
图片预览


文档简介
2024--2025学年度上期期末调研考试试卷
八年级数学
注意事项:
1.考试时间 100 分钟;本试卷共4页,计三大题 23 小题,满分 120 分;
2.本试卷上不要答题,请按答题卡上注意事项的要求直接把答案填写在答题卡上。答在
试卷上的答案无效。
一、选择题(每小题3分,共30分.下列各小题均有四个答案,其中只有一个是正确的)
1.中国文字博大精深,其中有许多是轴对称图形,以下四个文字中是轴对称图形的是( )
A.莲 B.城 C.光 D.山
2.如图,工人师傅安装门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法
的依据是( )
A.两点之间,线段最短
B.两点确定一条直线
C.垂线段最短
D.三角形的稳定性
3.已知三角形的两边长分别为5和9,则该三角形的第三边长可能是 ( )
A.3 B.4 C.5 D.14
4.下列运算,正确的是 ( )
A. a2 a3 = a6 B. (a2)5 = a10 C. (3a3)3 = 9a9 D. a8 ÷ a4 = a2
5.如图,这是被墨迹污染了一部分的三角形,王林根据所学的知识很快就画出了一个与
其全等的三角形,画图的依据是( )
A.SSS B.SAS C.AAS D.ASA
6.如图,折叠直角三角形纸片的直角,使点C落在AB边上的点E处.若BC = 24,∠B = 30 ,
则DE的长是( )
A.12 B.10 C.8 D.6
第5题图 第6题图
八年级数学试题 第1页(共 4页)
7.如图,在ΔABC中,∠ = 40 ,将ΔABC沿着直线l折叠,点C落在点D
的位置,则∠1-∠2的度数是 ( )
A.40° B.80° C.90° D.140°
6
8.已知关于x的方程 + = 1的解是非负数,则a的取值范围是( )
1 1
A.a>5 B.a≥5
C.a≥5且a≠6 D.a>5且a≠6
9.如图,在ΔABC中,AB=AC,∠ = 36 ,BD 平分∠ABC交AC于点D,
DE//AB交BC 于点E,EF//BD交CD于点F,则图中等腰三角形的个数为
( )
A.5个 B.6个 C.7个 D.8个
10.小明乘出租车去体育场,有两条线路可供选择,线路一的全程为25km,
但交通比较拥堵;线路二的全程为30km,平均车速比走线路一时的平均车速
高80%,因此能比走线路一少用10min到达.若设走线路一时的平均速度为x
km/h,根据题意可列方程( )
25 30 = 10 25 30A. B. = 10
(1+80%) 60 (1+80%)
30 25 = 10 30 25C. D. = 10
(1+80%) 60 (1+80%)
二、填空题 (共 5 小题,每小题 3 分,共 15 分)
0
11.若(x 1) =1,则x的取值范围是 .
12.一个多边形的每一个外角都为30 ,那么这个多边形的边数为 .
13.若(x+m)(2x+3)的乘积中不含x的一次项,则m的值为 .
14.如图,在ΔABC中,O是ΔABC内一点,且点O到ΔABC三边的距离相
等,∠BOC = 134 ,则∠A的度数为 .
15.在等腰三角形ABC中,AB=AC,AC的垂直平分线DE交直线AB于点E,交AC
于点D,连接CE,如果∠AEC = 80 ,那么∠B的度数为 .
八年级数学试题 第2页(共 4页)
三、解答题(共 8 小题,共 75 分)
16.(8分)计算与解方程.
2
(1) 计算:(x+y) (y+2x)(y 2x) ;
2x 1
(2) 解方程: = 1
x 2 2 x
(
2
17.(9分)先化简 x + 1) ÷ +22 ,再从-1,1,-2中选择合适的x值代入求值. +1 +2 +1
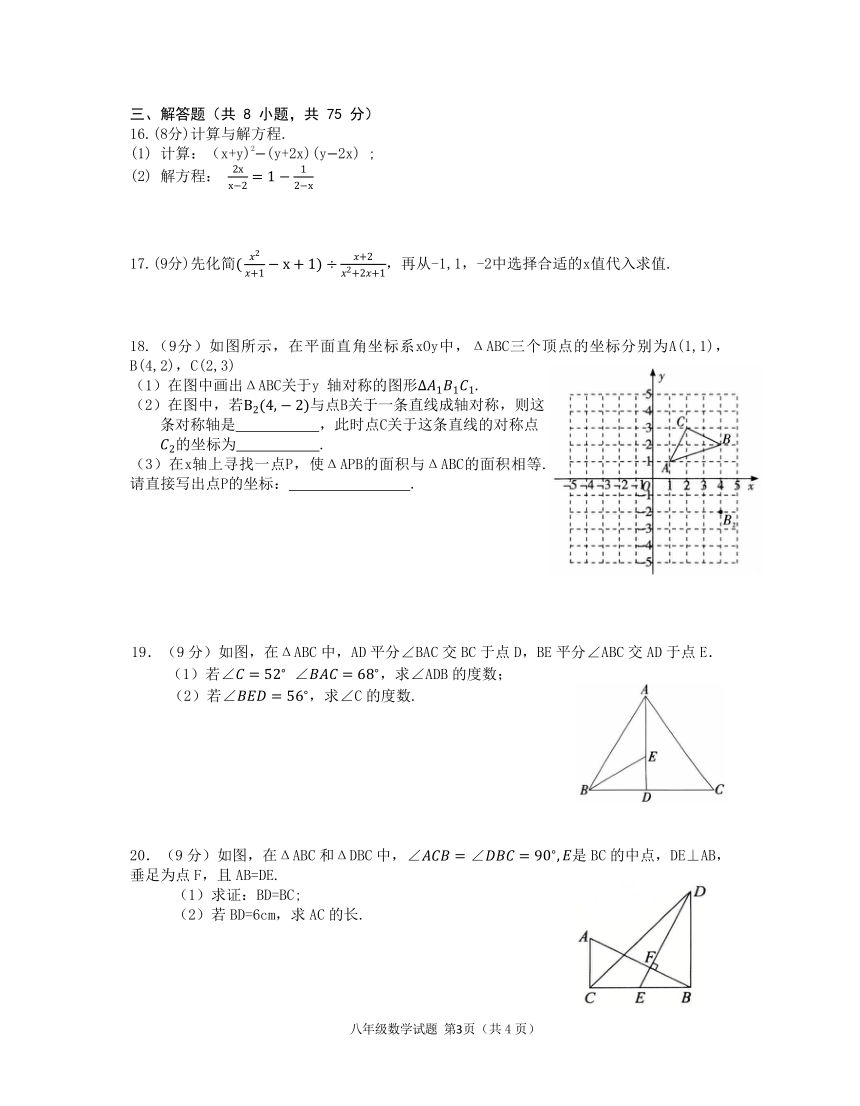
18.(9分)如图所示,在平面直角坐标系xOy中,ΔABC三个顶点的坐标分别为A(1,1),
B(4,2),C(2,3)
(1)在图中画出ΔABC关于y 轴对称的图形 1 1 1.
(2)在图中,若B2(4, 2)与点B关于一条直线成轴对称,则这
条对称轴是 ,此时点C关于这条直线的对称点
2的坐标为 .
(3)在x轴上寻找一点P,使ΔAPB的面积与ΔABC的面积相等.
请直接写出点P的坐标: .
19.(9分)如图,在ΔABC 中,AD 平分∠BAC 交 BC 于点 D,BE 平分∠ABC 交 AD 于点 E.
(1)若∠ = 52 ∠ = 68 ,求∠ADB 的度数;
(2)若∠ = 56 ,求∠C的度数.
20.(9 分)如图,在ΔABC 和ΔDBC 中,∠ = ∠ = 90 , 是 BC 的中点,DE⊥AB,
垂足为点 F,且 AB=DE.
(1)求证:BD=BC;
(2)若 BD=6cm,求 AC 的长.
八年级数学试题 第3页(共 4页)
21.(9分)某中学为落实《教育部办公厅关于进一步加强中小学生体质健康管理工作的
通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已
知每个篮球的价格比每个足球的价格贵30元,用4500元购买篮球的数量和用3000元购
买足球的数量相同,则每个篮球和每个足球的价格分别是多少元?
22.(10分)
(1)已知( )2 = 6, = 3,则 2 + 2 =
(2)如图,点C是线段AB上一点,以AC,BC为边分别向两边作正方形ACDE和正方形
BCFG.设AB =8,两正方形的面积和 1 + 2 = 36,求图中阴影部分的面积.
23.(12分)在ΔABC中,AB=AC,点D是射线CB上的一动点(不与点B,C重合),以AD为一
边在AD的右侧作ΔADE,,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠ = 90 时,那么∠DCE = 度.
(2)设∠BAC=α,∠DCE=β.
①如图2,当点D在线段CB上,∠ ≠ 90 时,请你探究α与β之间的数量关系,并证
明你的结论;
②如图3,当点D在线段CB的延长线上,∠ ≠ 90 时,请将图3补充完整,写出此时α
与β之间的数量关系并证明.
图 1 图 2 图 3
八年级数学试题 第4页(共 4页)
2024--2025学年度上期期末调研考试试卷
八年级数学参考答案
一、选择题
1、D 2、D 3、C 4、B 5、D 6、C 7、B 8、C 9、C 10、A
二、填空题
11. x≠1 12. 12 13. 3- 14. 88 15. 65 或 25
2
三、解答题
16. (1)解:原式 =x2+2xy+y2 - y2+4x2 (2分)
=5x2+2xy (4分)
(2)解:方程两边同乘(x-2),得2x=x-2+1.
解得x=-1. (3分)
检验:当x=-1时,x-2≠0.
所以原分式方程的解为x=-1. (4分)
2 2 2
17.解:( x x + 1) ÷ x+2 = x (x 1)(x+1)2
(x+1)
x+1 x +2x+1 x+1 x+2
1 (x + 1)2
=
x + 1 x + 2
= x+1 . (6分)
x+2
当x=1时,原式 = 1+1 = 2. (9分)
1+2 3
18.解:(1)如图,Δ 1 1 1即为所求. (2分)
(2)x轴(或横轴) (2,-3) (6分)
(3)(3,0) (9分)
19.解:(1)∵ ∠ = 68 , AD 平分∠BAC,
八年级数学答案 第1页(共 3页)
∴ ∠ = 1∠ = 34 .
2
∵ ∠ = 52 ∴ ∠ = ∠ +∠ = 86 .(4 分)
(2)∵ ∠ = 56 ∴ ∠ +∠ = 56 ,
∵AD 平分∠BAC,BE 平分∠ABC,∴∠ABC+∠ = 2∠ + 2∠ = 112 .
∴ ∠ = 180 (∠ +∠ ) = 68 . (9 分)
20. (1)∵DE⊥AB,可得∠BFE = 90 ,
∴ ∠ +∠ = 90 ,
∵∠ = 90 ,
∴ ∠ +∠ = 90 ,
∴∠A=∠DEB,
在ΔABC和ΔEDB中,
∠ACB = ∠DBC
∠A = ∠DEB
=
ΔABC≌ΔEDB (AAS),
∴BD=BC; (5分)
(2)∵ΔABC≌ΔEDB,
∴AC=BE,
∵E是BC的中点, BD=6cm,
1 1
∴ = = = 3 ,
2 2
∴AC=3cm. (9分)
21.解:设每个足球的价格是 x 元,则每个篮球的价格是(x+30)元.
4500
根据题意,得 = 3000 . (5 分)
+30
解得 x=60.
经检验,x=60 是所列方程的解,且符合题意.
∴x+30=90.
答:每个篮球的价格是 90 元,每个足球的价格是 60 元. (9 分)
22.解:(1)12 (3分)
(2)设AC=a,BC=b,
∵ = 8, 1 + 2 = 36,
∴a+b=8, 2 + 2 = 36. (5分)
∴ = 1 [( + )2 ( 2 + 2)]
2
= 1 × (64 36)
2
=14. (8分)
∴ 1阴影 = = 14 ×
1 = 7. (10分)
2 2
23.解:(1)90 (2分)
(2)① + = 180 .
∵∠BAD+∠DAC=α,
八年级数学答案 第2页(共 3页)
∠DAC+∠CAE=α,
∴∠BAD=∠CAE,
在ΔBAD和ΔCAE中
AB = AC
∠BAD = ∠CAE
AD = AE
∴ΔBAD≌ΔCAE(SAS),
∴∠ACE=∠B,
∵∠ +∠ = 180 ,
∴∠ = ∠ +∠ = 180 ,
∴ + = 180 ; (7分)
(3)作出图形,
∵∠BAD+∠BAE=α,
∠BAE+∠CAE=α,
∴∠BAD=∠CAE,
在ΔBAD和ΔCAE中,
AB = AC
∠BAD = ∠CAE
AD = AE
∴ΔBAD≌ΔCAE(SAS),
∴∠AEC=∠ADB,
∵∠ +∠ + = 180 ,
∠ +∠ + = 180 ,
∠CED=∠AEC+∠AED,
∴α=β. (12分)
八年级数学答案 第3页(共 3页)
八年级数学
注意事项:
1.考试时间 100 分钟;本试卷共4页,计三大题 23 小题,满分 120 分;
2.本试卷上不要答题,请按答题卡上注意事项的要求直接把答案填写在答题卡上。答在
试卷上的答案无效。
一、选择题(每小题3分,共30分.下列各小题均有四个答案,其中只有一个是正确的)
1.中国文字博大精深,其中有许多是轴对称图形,以下四个文字中是轴对称图形的是( )
A.莲 B.城 C.光 D.山
2.如图,工人师傅安装门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法
的依据是( )
A.两点之间,线段最短
B.两点确定一条直线
C.垂线段最短
D.三角形的稳定性
3.已知三角形的两边长分别为5和9,则该三角形的第三边长可能是 ( )
A.3 B.4 C.5 D.14
4.下列运算,正确的是 ( )
A. a2 a3 = a6 B. (a2)5 = a10 C. (3a3)3 = 9a9 D. a8 ÷ a4 = a2
5.如图,这是被墨迹污染了一部分的三角形,王林根据所学的知识很快就画出了一个与
其全等的三角形,画图的依据是( )
A.SSS B.SAS C.AAS D.ASA
6.如图,折叠直角三角形纸片的直角,使点C落在AB边上的点E处.若BC = 24,∠B = 30 ,
则DE的长是( )
A.12 B.10 C.8 D.6
第5题图 第6题图
八年级数学试题 第1页(共 4页)
7.如图,在ΔABC中,∠ = 40 ,将ΔABC沿着直线l折叠,点C落在点D
的位置,则∠1-∠2的度数是 ( )
A.40° B.80° C.90° D.140°
6
8.已知关于x的方程 + = 1的解是非负数,则a的取值范围是( )
1 1
A.a>5 B.a≥5
C.a≥5且a≠6 D.a>5且a≠6
9.如图,在ΔABC中,AB=AC,∠ = 36 ,BD 平分∠ABC交AC于点D,
DE//AB交BC 于点E,EF//BD交CD于点F,则图中等腰三角形的个数为
( )
A.5个 B.6个 C.7个 D.8个
10.小明乘出租车去体育场,有两条线路可供选择,线路一的全程为25km,
但交通比较拥堵;线路二的全程为30km,平均车速比走线路一时的平均车速
高80%,因此能比走线路一少用10min到达.若设走线路一时的平均速度为x
km/h,根据题意可列方程( )
25 30 = 10 25 30A. B. = 10
(1+80%) 60 (1+80%)
30 25 = 10 30 25C. D. = 10
(1+80%) 60 (1+80%)
二、填空题 (共 5 小题,每小题 3 分,共 15 分)
0
11.若(x 1) =1,则x的取值范围是 .
12.一个多边形的每一个外角都为30 ,那么这个多边形的边数为 .
13.若(x+m)(2x+3)的乘积中不含x的一次项,则m的值为 .
14.如图,在ΔABC中,O是ΔABC内一点,且点O到ΔABC三边的距离相
等,∠BOC = 134 ,则∠A的度数为 .
15.在等腰三角形ABC中,AB=AC,AC的垂直平分线DE交直线AB于点E,交AC
于点D,连接CE,如果∠AEC = 80 ,那么∠B的度数为 .
八年级数学试题 第2页(共 4页)
三、解答题(共 8 小题,共 75 分)
16.(8分)计算与解方程.
2
(1) 计算:(x+y) (y+2x)(y 2x) ;
2x 1
(2) 解方程: = 1
x 2 2 x
(
2
17.(9分)先化简 x + 1) ÷ +22 ,再从-1,1,-2中选择合适的x值代入求值. +1 +2 +1
18.(9分)如图所示,在平面直角坐标系xOy中,ΔABC三个顶点的坐标分别为A(1,1),
B(4,2),C(2,3)
(1)在图中画出ΔABC关于y 轴对称的图形 1 1 1.
(2)在图中,若B2(4, 2)与点B关于一条直线成轴对称,则这
条对称轴是 ,此时点C关于这条直线的对称点
2的坐标为 .
(3)在x轴上寻找一点P,使ΔAPB的面积与ΔABC的面积相等.
请直接写出点P的坐标: .
19.(9分)如图,在ΔABC 中,AD 平分∠BAC 交 BC 于点 D,BE 平分∠ABC 交 AD 于点 E.
(1)若∠ = 52 ∠ = 68 ,求∠ADB 的度数;
(2)若∠ = 56 ,求∠C的度数.
20.(9 分)如图,在ΔABC 和ΔDBC 中,∠ = ∠ = 90 , 是 BC 的中点,DE⊥AB,
垂足为点 F,且 AB=DE.
(1)求证:BD=BC;
(2)若 BD=6cm,求 AC 的长.
八年级数学试题 第3页(共 4页)
21.(9分)某中学为落实《教育部办公厅关于进一步加强中小学生体质健康管理工作的
通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已
知每个篮球的价格比每个足球的价格贵30元,用4500元购买篮球的数量和用3000元购
买足球的数量相同,则每个篮球和每个足球的价格分别是多少元?
22.(10分)
(1)已知( )2 = 6, = 3,则 2 + 2 =
(2)如图,点C是线段AB上一点,以AC,BC为边分别向两边作正方形ACDE和正方形
BCFG.设AB =8,两正方形的面积和 1 + 2 = 36,求图中阴影部分的面积.
23.(12分)在ΔABC中,AB=AC,点D是射线CB上的一动点(不与点B,C重合),以AD为一
边在AD的右侧作ΔADE,,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠ = 90 时,那么∠DCE = 度.
(2)设∠BAC=α,∠DCE=β.
①如图2,当点D在线段CB上,∠ ≠ 90 时,请你探究α与β之间的数量关系,并证
明你的结论;
②如图3,当点D在线段CB的延长线上,∠ ≠ 90 时,请将图3补充完整,写出此时α
与β之间的数量关系并证明.
图 1 图 2 图 3
八年级数学试题 第4页(共 4页)
2024--2025学年度上期期末调研考试试卷
八年级数学参考答案
一、选择题
1、D 2、D 3、C 4、B 5、D 6、C 7、B 8、C 9、C 10、A
二、填空题
11. x≠1 12. 12 13. 3- 14. 88 15. 65 或 25
2
三、解答题
16. (1)解:原式 =x2+2xy+y2 - y2+4x2 (2分)
=5x2+2xy (4分)
(2)解:方程两边同乘(x-2),得2x=x-2+1.
解得x=-1. (3分)
检验:当x=-1时,x-2≠0.
所以原分式方程的解为x=-1. (4分)
2 2 2
17.解:( x x + 1) ÷ x+2 = x (x 1)(x+1)2
(x+1)
x+1 x +2x+1 x+1 x+2
1 (x + 1)2
=
x + 1 x + 2
= x+1 . (6分)
x+2
当x=1时,原式 = 1+1 = 2. (9分)
1+2 3
18.解:(1)如图,Δ 1 1 1即为所求. (2分)
(2)x轴(或横轴) (2,-3) (6分)
(3)(3,0) (9分)
19.解:(1)∵ ∠ = 68 , AD 平分∠BAC,
八年级数学答案 第1页(共 3页)
∴ ∠ = 1∠ = 34 .
2
∵ ∠ = 52 ∴ ∠ = ∠ +∠ = 86 .(4 分)
(2)∵ ∠ = 56 ∴ ∠ +∠ = 56 ,
∵AD 平分∠BAC,BE 平分∠ABC,∴∠ABC+∠ = 2∠ + 2∠ = 112 .
∴ ∠ = 180 (∠ +∠ ) = 68 . (9 分)
20. (1)∵DE⊥AB,可得∠BFE = 90 ,
∴ ∠ +∠ = 90 ,
∵∠ = 90 ,
∴ ∠ +∠ = 90 ,
∴∠A=∠DEB,
在ΔABC和ΔEDB中,
∠ACB = ∠DBC
∠A = ∠DEB
=
ΔABC≌ΔEDB (AAS),
∴BD=BC; (5分)
(2)∵ΔABC≌ΔEDB,
∴AC=BE,
∵E是BC的中点, BD=6cm,
1 1
∴ = = = 3 ,
2 2
∴AC=3cm. (9分)
21.解:设每个足球的价格是 x 元,则每个篮球的价格是(x+30)元.
4500
根据题意,得 = 3000 . (5 分)
+30
解得 x=60.
经检验,x=60 是所列方程的解,且符合题意.
∴x+30=90.
答:每个篮球的价格是 90 元,每个足球的价格是 60 元. (9 分)
22.解:(1)12 (3分)
(2)设AC=a,BC=b,
∵ = 8, 1 + 2 = 36,
∴a+b=8, 2 + 2 = 36. (5分)
∴ = 1 [( + )2 ( 2 + 2)]
2
= 1 × (64 36)
2
=14. (8分)
∴ 1阴影 = = 14 ×
1 = 7. (10分)
2 2
23.解:(1)90 (2分)
(2)① + = 180 .
∵∠BAD+∠DAC=α,
八年级数学答案 第2页(共 3页)
∠DAC+∠CAE=α,
∴∠BAD=∠CAE,
在ΔBAD和ΔCAE中
AB = AC
∠BAD = ∠CAE
AD = AE
∴ΔBAD≌ΔCAE(SAS),
∴∠ACE=∠B,
∵∠ +∠ = 180 ,
∴∠ = ∠ +∠ = 180 ,
∴ + = 180 ; (7分)
(3)作出图形,
∵∠BAD+∠BAE=α,
∠BAE+∠CAE=α,
∴∠BAD=∠CAE,
在ΔBAD和ΔCAE中,
AB = AC
∠BAD = ∠CAE
AD = AE
∴ΔBAD≌ΔCAE(SAS),
∴∠AEC=∠ADB,
∵∠ +∠ + = 180 ,
∠ +∠ + = 180 ,
∠CED=∠AEC+∠AED,
∴α=β. (12分)
八年级数学答案 第3页(共 3页)
同课章节目录
