山东省德州市武城县2024—2025学年上学期期末考试九年级数学试题(无答案)
文档属性
| 名称 | 山东省德州市武城县2024—2025学年上学期期末考试九年级数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 737.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-15 21:12:45 | ||
图片预览


文档简介
武城县2024-2025学年度第一学期期末教学质量监测
九年级数学试题
(考试时间120分钟 满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.请将选择题答案用2B铅笔填涂在答题卡指定题号里,将非选择题的答案用0.5毫米黑色签字笔直接答在答题卡上对应的答题区域内,答在试题卷上无效.
3.考生必须保持答题卡的整洁,不能使用涂改液、胶带纸、修正带.
一、选择题(本大题共12个小题每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.刺绣是中国民间传统手工艺之一,下列刺绣图案中,是中心对称图形的为( )
A. B.
C. D.
2.在下列事件中,必然事件是( )
A.掷一次骰子,向上一面的点数是3 B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯 D.任意画一个三角形,其内角和是180°
3.如图,在直角坐标系中,的三个顶点分别为,,,现以原点为位似中心,在第一象限内作与的位似比为2的位似图形,则顶点的坐标是( )
A. B. C. D.
4.将抛物线向下平移2个单位后,所得新抛物线的顶点式为( )
A. B.
C. D.
5.关于的一元二次方程有两个不相等的实数根,则实数的取值范围是( )
A.且 B. C.且 D.
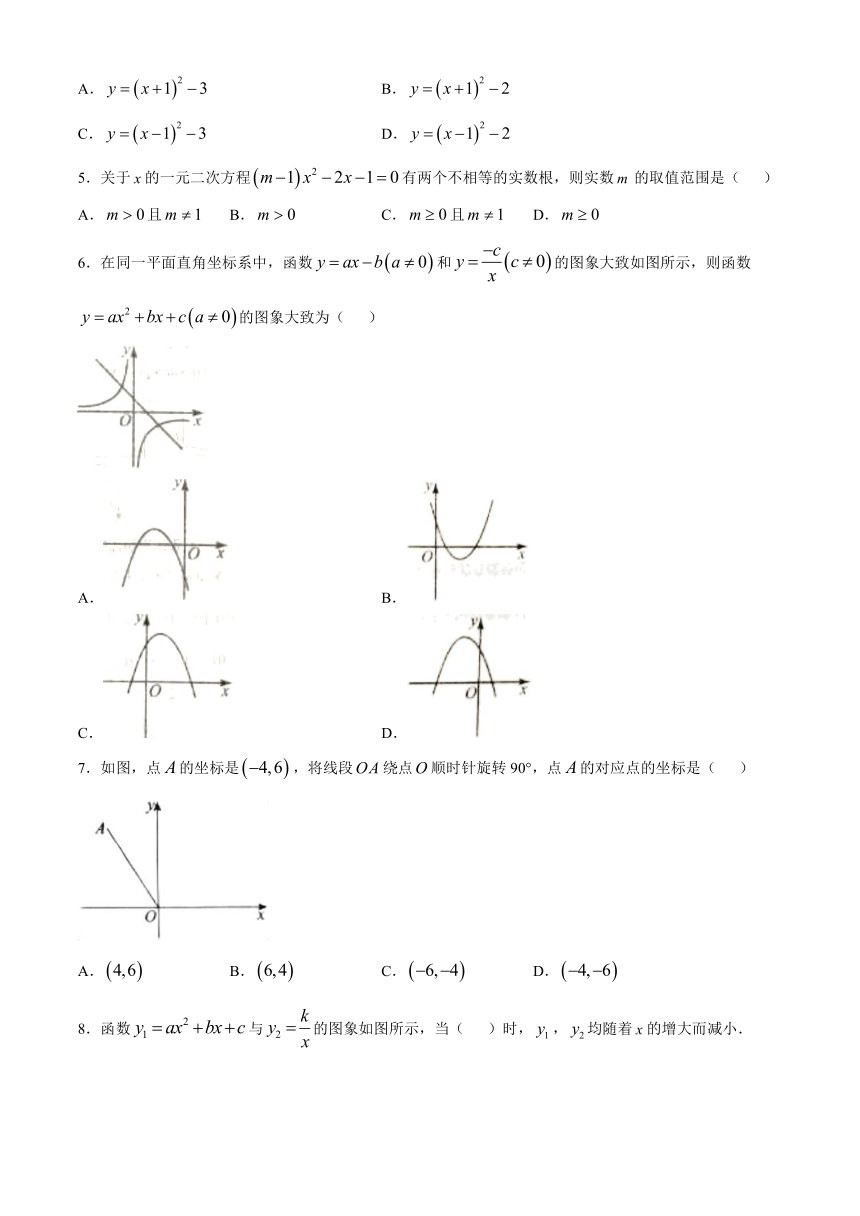
6.在同一平面直角坐标系中,函数和的图象大致如图所示,则函数的图象大致为( )
A. B.
C. D.
7.如图,点的坐标是,将线段绕点顺时针旋转90°,点的对应点的坐标是( )
A. B. C. D.
8.函数与的图象如图所示,当( )时,,均随着的增大而减小.
A. B. C. D.
9.点、、在上的位置如图所示,,的半径为3,则的长是( )
A. B. C. D.
10.如图,在平面直角坐标系中,点,,,,若点在函数的图象上,则的值为( )
A.6 B.8 C.10 D.12
11.如图,在平面直角坐标系中,过点且垂直于轴的直线与反比例函数的图像交于点,将直线绕点逆时针旋转45°,所得的直线经过第一、二、四象限,则的取值范围是( )
A.或 B.且
C.或 D.或
12.如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下列四个结论:①;②;③;④若,则,其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6个小题,共24分)
13.已知方程的两根分别为,,则的值为______.
14.如图,正八边形转盘被分成八个面积相等的三角形,任意转动这个转盘一次,当转盘停止转动时,指针落在阴影部分的概率是______.
15.点关于原点对称的点的坐标是______.
16.如图,在中,,,为边的中线,以为圆心,线段长为半径画弧,交轴正半轴于点,则点的坐标为______.
17.中国古人发明利用物体的影子确定四季的工具——土圭,具体方法是在平台中央竖立一根杆子,尺,观察杆子的日影长度.古代的人们发现,夏至时日影最短,冬至日影最长,这样通过日影的长度得到夏至和冬至,确定了四季.如图,利用土圭之法记录了两个时刻杆的影长,发现第一时刻光线与杆的夹角,和第二时刻光线与地面的夹角相等,测得第二时刻的影长为24尺,则第一时刻的影长为______尺.
18.如图,一段抛物线,记为,它与轴交于点,;将绕点旋转180°得,交轴于点;将绕点旋转180°得,交轴于点;……如此进行下去,得到一“波浪线”,若点在此“波浪线”上,则的值为______.
三、解答题(本大题有7小题,共78分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)2024年巴黎奥运会新增了四个项目:霹雳舞,滑板,冲浪,运动攀岩,依次记为,,,,武城县体育队的小明同学把这四个项目写在了背面完全相同的卡片上,将这四张卡片背面朝上,洗匀放好.
(1)小明想从中随机抽取一张,去了解该项目在奥运会中的得分标准,恰好抽到是(滑板)的概率是______.
(2)体育老师想从中选出来两个项目,让小明做成手抄报给大家普及一下,他先从中随机抽取一张不放回,再从中随机抽取一张,请用列表法或画树状图法表示出所有可能的结果,并求体育老师抽到的两张卡片恰好是(滑板)和(运动攀岩)的概率.
20.(10分)“杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.
(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;
(2)按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.
21.(10分)如图,在中,,是上一点,,.
(1)求证:;
(2)若,,的面积为2,求的面积.
22.(12分)如图,一次函数的图象与反比例函数的图象相交于,两点.
(1)求一次函数和反比例函数的解析式;
(2)请直接写出满足的取值范围.
23.(12分)如图,圆内接四边形的对角线,交于点,平分,.
(1)求的大小;
(2)过点作交的延长线于点,若,,求圆的半径.
24.如图,矩形中,,将一块直角三角板的直角顶点放在两对角线,的交点处,以点为旋转中心转动三角板,并保证三角板的两直角边分别于边,所在的直线相交,交点分别为,.
图1 图2 图3
(1)当,时,如图1,则的值为______;
(2)现将三角板绕点逆时针旋转角,如图2,求的值;
(3)在(2)的基础上继续旋转,当,且使时,如图3,的值是否变化?证明你的结论.
25.(14分)【定义与性质】
如图,记二次函数和的图象分别为抛物线和.
定义:若抛物线的顶点在抛物线上,则称是的伴随抛物线.
性质:①一条抛物线有无数条伴随抛物线;
②若是的伴随抛物线,则也是的伴随抛物线,即的顶点在上.
【理解与运用】
(1)若二次函数和的图象都是抛物线的伴随抛物线,则______,______.
【思考与探究】
(2)设函数的图象为抛物线.
①若函数的图象为抛物线,且始终是的伴随抛物线,求,的值;
②若抛物线与轴有两个不同的交点,,请直接写出的取值范围.
九年级数学试题
(考试时间120分钟 满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.请将选择题答案用2B铅笔填涂在答题卡指定题号里,将非选择题的答案用0.5毫米黑色签字笔直接答在答题卡上对应的答题区域内,答在试题卷上无效.
3.考生必须保持答题卡的整洁,不能使用涂改液、胶带纸、修正带.
一、选择题(本大题共12个小题每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.刺绣是中国民间传统手工艺之一,下列刺绣图案中,是中心对称图形的为( )
A. B.
C. D.
2.在下列事件中,必然事件是( )
A.掷一次骰子,向上一面的点数是3 B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯 D.任意画一个三角形,其内角和是180°
3.如图,在直角坐标系中,的三个顶点分别为,,,现以原点为位似中心,在第一象限内作与的位似比为2的位似图形,则顶点的坐标是( )
A. B. C. D.
4.将抛物线向下平移2个单位后,所得新抛物线的顶点式为( )
A. B.
C. D.
5.关于的一元二次方程有两个不相等的实数根,则实数的取值范围是( )
A.且 B. C.且 D.
6.在同一平面直角坐标系中,函数和的图象大致如图所示,则函数的图象大致为( )
A. B.
C. D.
7.如图,点的坐标是,将线段绕点顺时针旋转90°,点的对应点的坐标是( )
A. B. C. D.
8.函数与的图象如图所示,当( )时,,均随着的增大而减小.
A. B. C. D.
9.点、、在上的位置如图所示,,的半径为3,则的长是( )
A. B. C. D.
10.如图,在平面直角坐标系中,点,,,,若点在函数的图象上,则的值为( )
A.6 B.8 C.10 D.12
11.如图,在平面直角坐标系中,过点且垂直于轴的直线与反比例函数的图像交于点,将直线绕点逆时针旋转45°,所得的直线经过第一、二、四象限,则的取值范围是( )
A.或 B.且
C.或 D.或
12.如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下列四个结论:①;②;③;④若,则,其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6个小题,共24分)
13.已知方程的两根分别为,,则的值为______.
14.如图,正八边形转盘被分成八个面积相等的三角形,任意转动这个转盘一次,当转盘停止转动时,指针落在阴影部分的概率是______.
15.点关于原点对称的点的坐标是______.
16.如图,在中,,,为边的中线,以为圆心,线段长为半径画弧,交轴正半轴于点,则点的坐标为______.
17.中国古人发明利用物体的影子确定四季的工具——土圭,具体方法是在平台中央竖立一根杆子,尺,观察杆子的日影长度.古代的人们发现,夏至时日影最短,冬至日影最长,这样通过日影的长度得到夏至和冬至,确定了四季.如图,利用土圭之法记录了两个时刻杆的影长,发现第一时刻光线与杆的夹角,和第二时刻光线与地面的夹角相等,测得第二时刻的影长为24尺,则第一时刻的影长为______尺.
18.如图,一段抛物线,记为,它与轴交于点,;将绕点旋转180°得,交轴于点;将绕点旋转180°得,交轴于点;……如此进行下去,得到一“波浪线”,若点在此“波浪线”上,则的值为______.
三、解答题(本大题有7小题,共78分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)2024年巴黎奥运会新增了四个项目:霹雳舞,滑板,冲浪,运动攀岩,依次记为,,,,武城县体育队的小明同学把这四个项目写在了背面完全相同的卡片上,将这四张卡片背面朝上,洗匀放好.
(1)小明想从中随机抽取一张,去了解该项目在奥运会中的得分标准,恰好抽到是(滑板)的概率是______.
(2)体育老师想从中选出来两个项目,让小明做成手抄报给大家普及一下,他先从中随机抽取一张不放回,再从中随机抽取一张,请用列表法或画树状图法表示出所有可能的结果,并求体育老师抽到的两张卡片恰好是(滑板)和(运动攀岩)的概率.
20.(10分)“杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.
(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;
(2)按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.
21.(10分)如图,在中,,是上一点,,.
(1)求证:;
(2)若,,的面积为2,求的面积.
22.(12分)如图,一次函数的图象与反比例函数的图象相交于,两点.
(1)求一次函数和反比例函数的解析式;
(2)请直接写出满足的取值范围.
23.(12分)如图,圆内接四边形的对角线,交于点,平分,.
(1)求的大小;
(2)过点作交的延长线于点,若,,求圆的半径.
24.如图,矩形中,,将一块直角三角板的直角顶点放在两对角线,的交点处,以点为旋转中心转动三角板,并保证三角板的两直角边分别于边,所在的直线相交,交点分别为,.
图1 图2 图3
(1)当,时,如图1,则的值为______;
(2)现将三角板绕点逆时针旋转角,如图2,求的值;
(3)在(2)的基础上继续旋转,当,且使时,如图3,的值是否变化?证明你的结论.
25.(14分)【定义与性质】
如图,记二次函数和的图象分别为抛物线和.
定义:若抛物线的顶点在抛物线上,则称是的伴随抛物线.
性质:①一条抛物线有无数条伴随抛物线;
②若是的伴随抛物线,则也是的伴随抛物线,即的顶点在上.
【理解与运用】
(1)若二次函数和的图象都是抛物线的伴随抛物线,则______,______.
【思考与探究】
(2)设函数的图象为抛物线.
①若函数的图象为抛物线,且始终是的伴随抛物线,求,的值;
②若抛物线与轴有两个不同的交点,,请直接写出的取值范围.
同课章节目录
