湖南省双峰县沙塘乡中心学校2014-2015学年八年级下学期期中测试数学试题
文档属性
| 名称 | 湖南省双峰县沙塘乡中心学校2014-2015学年八年级下学期期中测试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 63.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-20 14:13:56 | ||
图片预览


文档简介
八年级下册期中数学测试题
精心选一选,旗开得胜(本大题共10道小题,每小题3分,满分30分)
1. 两个直角三角形全等的条件是( )
A.一锐角对应相等 ; B.两锐角对应相等;
C.一条边对应相等; D.两条边对应相等
2. 一个三角形的三边长为,,,则此三角形最大边上的高为( )
A. B. C. D.
3. 已知x、y为正数,且│x2-4│+ ( http: / / www.21cnjy.com )(y2-3)2=0,如果以x、y的长为直角边作一个直角三角形,那么以此直角三角形的斜边为边长的正方形的面积为( );
A、5 B、25 C、7 D、15
4. 下列各组线段中的三个长度①9、12、 ( http: / / www.21cnjy.com )15;②7、24、25;③32、42、52;④3a、4a、5a(a>0);⑤m2-n2、2mn、m2+n2(m、n为正整数,且m>n)其中可以构成直角三角形的有( );
A、5组; B、4组; C、3组; D、2组
5. 用两块完全相同的直角三角形拼下列图形:①平行四边形 ②矩形 ③菱形 ④正方形 ⑤等腰三角形 ⑥等边三角形,一定能拼成的图形是( ).
A ①④⑤ B ②⑤⑥ C ①②③ D ①②⑤
6. 顺次连结矩形四边中点所得的四边形一定是( ).
A 平行四边形 B 矩形 C 菱形 D 正方形
7. 如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长( ).
A 1 B 1.5 C 2 D 3
8. 如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是( ).
A 3:4 B 5:8 C 9:16 D 1:2
9. 下列图形中,是中心对称图形的是( )
( http: / / www.21cnjy.com )
A B C D
10. 如图,矩形纸片ABCD中,已知AD ( http: / / www.21cnjy.com )=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4 C.5 D.6
细心填一填,一锤定音(本大题共8道小题,每小题4分,满分32分)
11. 在RtABC中,∠C=90°,∠A=75°,则∠B= .
12. 在RtABC中,∠C=90°,AB=24㎝,D为AB的中点,则CD= ㎝.
13. 四根小木棒的长分别为5cm,8cm,12cm,13cm,任选三根组成三角形,其中有 个直角三角形
14. 在△ABC中,AB=8cm,BC=15cm,要使∠B=90°,则AC的长必为______cm.
15. 一个多边形的每一个外角等于40°,则此多边形是 边形,它的内角和等于 。
16. 如图,已知:在AB ( http: / / www.21cnjy.com )CD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=______cm.
( http: / / www.21cnjy.com )
17. 在正方形ABCD处,以BC为边作一个等边三角形△BCE,则∠DCE=
18. 如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是 .
( http: / / www.21cnjy.com )
三、用心做一做,慧眼识金(本大题共3道小题,每小题7分,满分21分)
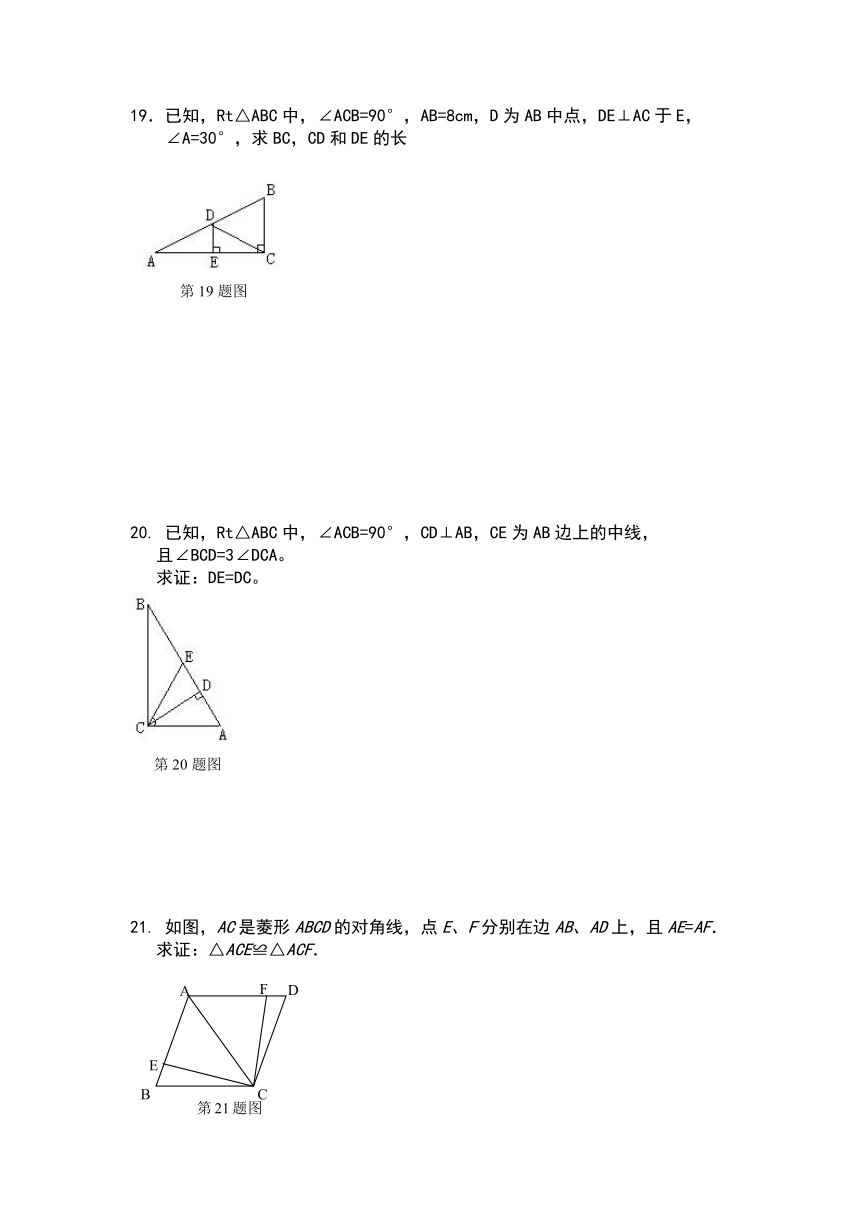
19.已知,Rt△ABC中,∠ACB=90°,AB=8cm,D为AB中点,DE⊥AC于E,
∠A=30°,求BC,CD和DE的长
20. 已知,Rt△ABC中,∠ACB=90°,CD⊥AB,CE为AB边上的中线,
且∠BCD=3∠DCA。
求证:DE=DC。
( http: / / www.21cnjy.com )
21. 如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.
求证:△ACE≌△ACF.
四、综合用一用,马到成功(本大题共1道小题,满分7分)
22. 如图,在△ABC中,点O是AC ( http: / / www.21cnjy.com )边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF。那么当点O运动到何下时,四边形AECF是矩形?并证明你的结论。
五、耐心想一想,再接再厉(本大题共1道小题,满分10分)
23已知:如图,在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF。
⑴△BCE与△DCF全等吗?说明理由;
⑵若∠BEC=60o,求∠EFD。
参考答案
一、选择题
题序 1 2 3 4 5 6 7 8 9 10
答案 D B C B D C C B A D
二、填空题
11、15°
12、12
13、1
14、17
15、1260°
16、3
17、150°
18、2
三、
19、解:在Rt△ABC中
∵∠ACB=90 ∠A=30°∴
∵AB=8 ∴BC=4
∵D为AB中点,CD为中线
∴
∵DE⊥AC,∴∠AED=90°
在Rt△ADE中,,
∴
20、证明:∵∠BCD=3∠DCA且∠BCA=90°
∴∠DCA=22. 5°∠BCD=67.5°∠B=22.5°
∴∠CEA=45°∠ECD=67.5°-22.5°=45°
∴DE=DC
21、证明:∵四边形ABCD为菱形
∴∠BAC=∠DAC
又∵AE=AF,AC=AC
∴△ACE≌△ACF(SAS)
四、
22、当点O运动到AC的中点(或OA=OC)时,
四边形AECF是矩形
证明:∵CE平分∠BCA,∴∠1=∠2,
又∵MN∥BC, ∴∠1=∠3,
∴∠3=∠2,∴EO=CO.
同理,FO=CO
∴EO=FO
又OA=OC, ∴四边形AECF是平行四边形
又∵∠1=∠2,∠4=∠5,
∴∠1+∠5=∠2+∠4.
又∵∠1+∠5+∠2+∠4=180°
∴∠2+∠4=90°
∴四边形AECF是矩形
五
23、(1) △BCE≌△DCF,用SAS即可证明。
(2)∠EFD=15°
A
B
C
D
第8题
第7题
A
B
C
D
E
(第10题图)
第17题图
第19题图
第20题图
第21题图
A
B
C
D
E
F
(第22题图)
第23题图
精心选一选,旗开得胜(本大题共10道小题,每小题3分,满分30分)
1. 两个直角三角形全等的条件是( )
A.一锐角对应相等 ; B.两锐角对应相等;
C.一条边对应相等; D.两条边对应相等
2. 一个三角形的三边长为,,,则此三角形最大边上的高为( )
A. B. C. D.
3. 已知x、y为正数,且│x2-4│+ ( http: / / www.21cnjy.com )(y2-3)2=0,如果以x、y的长为直角边作一个直角三角形,那么以此直角三角形的斜边为边长的正方形的面积为( );
A、5 B、25 C、7 D、15
4. 下列各组线段中的三个长度①9、12、 ( http: / / www.21cnjy.com )15;②7、24、25;③32、42、52;④3a、4a、5a(a>0);⑤m2-n2、2mn、m2+n2(m、n为正整数,且m>n)其中可以构成直角三角形的有( );
A、5组; B、4组; C、3组; D、2组
5. 用两块完全相同的直角三角形拼下列图形:①平行四边形 ②矩形 ③菱形 ④正方形 ⑤等腰三角形 ⑥等边三角形,一定能拼成的图形是( ).
A ①④⑤ B ②⑤⑥ C ①②③ D ①②⑤
6. 顺次连结矩形四边中点所得的四边形一定是( ).
A 平行四边形 B 矩形 C 菱形 D 正方形
7. 如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长( ).
A 1 B 1.5 C 2 D 3
8. 如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是( ).
A 3:4 B 5:8 C 9:16 D 1:2
9. 下列图形中,是中心对称图形的是( )
( http: / / www.21cnjy.com )
A B C D
10. 如图,矩形纸片ABCD中,已知AD ( http: / / www.21cnjy.com )=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4 C.5 D.6
细心填一填,一锤定音(本大题共8道小题,每小题4分,满分32分)
11. 在RtABC中,∠C=90°,∠A=75°,则∠B= .
12. 在RtABC中,∠C=90°,AB=24㎝,D为AB的中点,则CD= ㎝.
13. 四根小木棒的长分别为5cm,8cm,12cm,13cm,任选三根组成三角形,其中有 个直角三角形
14. 在△ABC中,AB=8cm,BC=15cm,要使∠B=90°,则AC的长必为______cm.
15. 一个多边形的每一个外角等于40°,则此多边形是 边形,它的内角和等于 。
16. 如图,已知:在AB ( http: / / www.21cnjy.com )CD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=______cm.
( http: / / www.21cnjy.com )
17. 在正方形ABCD处,以BC为边作一个等边三角形△BCE,则∠DCE=
18. 如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是 .
( http: / / www.21cnjy.com )
三、用心做一做,慧眼识金(本大题共3道小题,每小题7分,满分21分)
19.已知,Rt△ABC中,∠ACB=90°,AB=8cm,D为AB中点,DE⊥AC于E,
∠A=30°,求BC,CD和DE的长
20. 已知,Rt△ABC中,∠ACB=90°,CD⊥AB,CE为AB边上的中线,
且∠BCD=3∠DCA。
求证:DE=DC。
( http: / / www.21cnjy.com )
21. 如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.
求证:△ACE≌△ACF.
四、综合用一用,马到成功(本大题共1道小题,满分7分)
22. 如图,在△ABC中,点O是AC ( http: / / www.21cnjy.com )边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF。那么当点O运动到何下时,四边形AECF是矩形?并证明你的结论。
五、耐心想一想,再接再厉(本大题共1道小题,满分10分)
23已知:如图,在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF。
⑴△BCE与△DCF全等吗?说明理由;
⑵若∠BEC=60o,求∠EFD。
参考答案
一、选择题
题序 1 2 3 4 5 6 7 8 9 10
答案 D B C B D C C B A D
二、填空题
11、15°
12、12
13、1
14、17
15、1260°
16、3
17、150°
18、2
三、
19、解:在Rt△ABC中
∵∠ACB=90 ∠A=30°∴
∵AB=8 ∴BC=4
∵D为AB中点,CD为中线
∴
∵DE⊥AC,∴∠AED=90°
在Rt△ADE中,,
∴
20、证明:∵∠BCD=3∠DCA且∠BCA=90°
∴∠DCA=22. 5°∠BCD=67.5°∠B=22.5°
∴∠CEA=45°∠ECD=67.5°-22.5°=45°
∴DE=DC
21、证明:∵四边形ABCD为菱形
∴∠BAC=∠DAC
又∵AE=AF,AC=AC
∴△ACE≌△ACF(SAS)
四、
22、当点O运动到AC的中点(或OA=OC)时,
四边形AECF是矩形
证明:∵CE平分∠BCA,∴∠1=∠2,
又∵MN∥BC, ∴∠1=∠3,
∴∠3=∠2,∴EO=CO.
同理,FO=CO
∴EO=FO
又OA=OC, ∴四边形AECF是平行四边形
又∵∠1=∠2,∠4=∠5,
∴∠1+∠5=∠2+∠4.
又∵∠1+∠5+∠2+∠4=180°
∴∠2+∠4=90°
∴四边形AECF是矩形
五
23、(1) △BCE≌△DCF,用SAS即可证明。
(2)∠EFD=15°
A
B
C
D
第8题
第7题
A
B
C
D
E
(第10题图)
第17题图
第19题图
第20题图
第21题图
A
B
C
D
E
F
(第22题图)
第23题图
同课章节目录
