人教A版 选择性必修第三册6.3.1 二项式定理 课件(共16张PPT)
文档属性
| 名称 | 人教A版 选择性必修第三册6.3.1 二项式定理 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 40.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-17 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
二项式定理应用
一、掌握二项展开式及通项公式的应用。
三、理解和初步掌握赋值法及其应用。
二、理解掌握二项式系数的性质,并会进行简单应用。
四、能灵活运用二项式系数的性质求二项式展开式系数的最大项。
学习目标
1、二项式定理
试写出二项式定理的展开式
要点梳理
特征总结:
1、展开式共有( )项
2、按a的( )排列;按b的( )排列
3、an-rbr是第( )项。
通项公式
=
二项式系数
(r=0、1、2、3、3…、n)
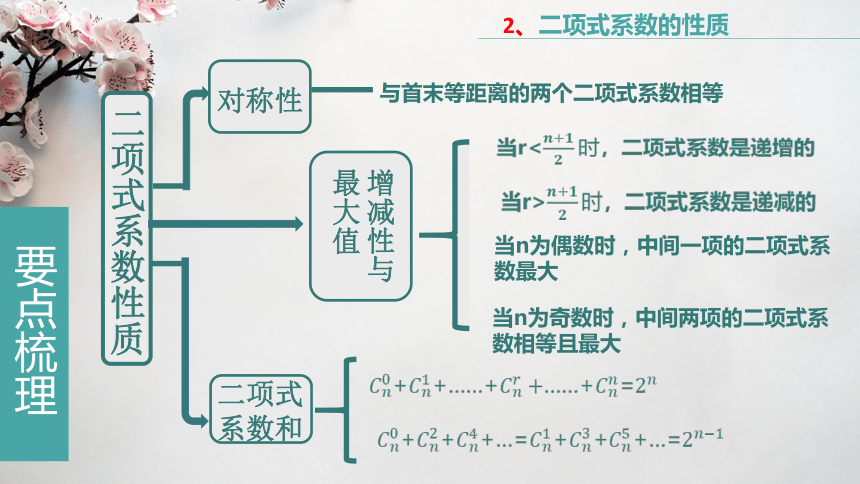
2、二项式系数的性质
二项式系数性质
对称性
二项式系数和
当n为偶数时,中间一项的二项式系数最大
当r<,二项式系数是递增的
当r>,二项式系数是递减的
当n为奇数时,中间两项的二项式系数相等且最大
增减性与最大值
与首末等距离的两个二项式系数相等
++……+……+=
+++…=+++…=
要点梳理
二项展开式中特定项或特定项的系数
(1)(x- 的二项展开式中的常数项为________;
(2)(2013·高考安徽卷)若(x+)8的展开式中,x4的系数为7,则实数a=________.
典型例题
15
课堂笔记
二项展开式中特定项或特定项的系数
求二项展开式中的项
或项的系数的方法
(1)展开式中常数项、有理项的特征是通项中未知数的指数分别为零和整数.解决这类问题时,先要合并通项中同一字母的指数,再根据上述特征进行分析.
(2)有关求二项展开式中的项、系数、参数值或取值范围等,一般要利用通项公式,运用方程思想进行求值,通过解不等式(组)求取值范围.
方法感悟
二项展开式中特定项或特定项的系数
二项式系数的性质
(1)(1+2x)15的二项展开式中系数最大的项为( )
A.第8项 B.第9项 C.第8项和第9项 D.第11项
(2)(安徽省“江南十校”联考)若(x+2+m)9=a0+a1(x+1)+a2(x+1)2+…+a9(x+1)9,且(a0+a2+…+a8)2-(a1+a3+…+a9)2=39,则实数m的值为( )
A.1或-3 B.-1或3 C.1 D.-3
典型例题
D
A
课堂笔记
二项式系数的性质
求二项展开式中的值
或项的系数最大值的方法
方法感悟
(1)二项式定理给出的是一个恒等式,对于a,b的一切值都成立.因此,可将a,b设定为一些特殊的值.在使用赋值法时,令a,b等于多少时,应视具体情况而定,一般取“1、-1或0”,有时也取其他值.
(2)求展开式系数最大项:如求(a+bx)n(a、b∈R)的展开式系数最大的项,一般是采用待定系数法,设展开式各项系数分别为A1,A2,…,An+1,且第k项系数最大,应用不等式组,从而解出k值.
二项式系数的性质
二项式定理的综合应用
(高考湖北卷)设a∈Z,且0≤a<13,若512 012+a 能被13整除,则a=( )
A.0 B.1 C.11 D.12
Photoshop Cs6
典型例题
D
课堂笔记
二项式定理的综合应用
解决二项式整除问题
或求余数问题的方法
方法感悟
二项式定理的综合应用
(1)利用二项式定理解决整除问题时,关键是进行合理地变形构造二项式,应注意:要证明一个式子能被另一个式子整除,只要证明这个式子按二项式定理展开后的各项均能被另一个式子整除即可.
(2)求余数问题时,应明确被除式f(x)与除式g(x)(g(x)≠0),商式q(x)与余式的关系及余式的范围.
当堂检测
(1)(东北三校联考)若(-)n的展开式中第四项为常数项,
则n=( )
A.4 B.5 C.6 D.7
(2)如果(x2-)n的展开式中只有第4项的二项式系数最大,那么展开式中的所有项的系数之和是( )
A.0 B.256 C.64 D.
(3)(1+2x)n(其中n∈N且n≥6)的展开式中x3与x4项的二项式系数相等,则
系数最大项为________.
B
D
当堂检测
课堂小结
1、运用通项公式求特定项或特定项的系数等
2、运用二项式系数的性质求二项式系数最大值
3、赋值法求各项系数和等问题
4、运用二项式定理解决整除或余数问题
二项式定理应用
一、掌握二项展开式及通项公式的应用。
三、理解和初步掌握赋值法及其应用。
二、理解掌握二项式系数的性质,并会进行简单应用。
四、能灵活运用二项式系数的性质求二项式展开式系数的最大项。
学习目标
1、二项式定理
试写出二项式定理的展开式
要点梳理
特征总结:
1、展开式共有( )项
2、按a的( )排列;按b的( )排列
3、an-rbr是第( )项。
通项公式
=
二项式系数
(r=0、1、2、3、3…、n)
2、二项式系数的性质
二项式系数性质
对称性
二项式系数和
当n为偶数时,中间一项的二项式系数最大
当r<,二项式系数是递增的
当r>,二项式系数是递减的
当n为奇数时,中间两项的二项式系数相等且最大
增减性与最大值
与首末等距离的两个二项式系数相等
++……+……+=
+++…=+++…=
要点梳理
二项展开式中特定项或特定项的系数
(1)(x- 的二项展开式中的常数项为________;
(2)(2013·高考安徽卷)若(x+)8的展开式中,x4的系数为7,则实数a=________.
典型例题
15
课堂笔记
二项展开式中特定项或特定项的系数
求二项展开式中的项
或项的系数的方法
(1)展开式中常数项、有理项的特征是通项中未知数的指数分别为零和整数.解决这类问题时,先要合并通项中同一字母的指数,再根据上述特征进行分析.
(2)有关求二项展开式中的项、系数、参数值或取值范围等,一般要利用通项公式,运用方程思想进行求值,通过解不等式(组)求取值范围.
方法感悟
二项展开式中特定项或特定项的系数
二项式系数的性质
(1)(1+2x)15的二项展开式中系数最大的项为( )
A.第8项 B.第9项 C.第8项和第9项 D.第11项
(2)(安徽省“江南十校”联考)若(x+2+m)9=a0+a1(x+1)+a2(x+1)2+…+a9(x+1)9,且(a0+a2+…+a8)2-(a1+a3+…+a9)2=39,则实数m的值为( )
A.1或-3 B.-1或3 C.1 D.-3
典型例题
D
A
课堂笔记
二项式系数的性质
求二项展开式中的值
或项的系数最大值的方法
方法感悟
(1)二项式定理给出的是一个恒等式,对于a,b的一切值都成立.因此,可将a,b设定为一些特殊的值.在使用赋值法时,令a,b等于多少时,应视具体情况而定,一般取“1、-1或0”,有时也取其他值.
(2)求展开式系数最大项:如求(a+bx)n(a、b∈R)的展开式系数最大的项,一般是采用待定系数法,设展开式各项系数分别为A1,A2,…,An+1,且第k项系数最大,应用不等式组,从而解出k值.
二项式系数的性质
二项式定理的综合应用
(高考湖北卷)设a∈Z,且0≤a<13,若512 012+a 能被13整除,则a=( )
A.0 B.1 C.11 D.12
Photoshop Cs6
典型例题
D
课堂笔记
二项式定理的综合应用
解决二项式整除问题
或求余数问题的方法
方法感悟
二项式定理的综合应用
(1)利用二项式定理解决整除问题时,关键是进行合理地变形构造二项式,应注意:要证明一个式子能被另一个式子整除,只要证明这个式子按二项式定理展开后的各项均能被另一个式子整除即可.
(2)求余数问题时,应明确被除式f(x)与除式g(x)(g(x)≠0),商式q(x)与余式的关系及余式的范围.
当堂检测
(1)(东北三校联考)若(-)n的展开式中第四项为常数项,
则n=( )
A.4 B.5 C.6 D.7
(2)如果(x2-)n的展开式中只有第4项的二项式系数最大,那么展开式中的所有项的系数之和是( )
A.0 B.256 C.64 D.
(3)(1+2x)n(其中n∈N且n≥6)的展开式中x3与x4项的二项式系数相等,则
系数最大项为________.
B
D
当堂检测
课堂小结
1、运用通项公式求特定项或特定项的系数等
2、运用二项式系数的性质求二项式系数最大值
3、赋值法求各项系数和等问题
4、运用二项式定理解决整除或余数问题
