高二选择性必修二 5.1.1 变化率问题 课件(共17张PPT)
文档属性
| 名称 | 高二选择性必修二 5.1.1 变化率问题 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-17 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第五章一元函数的导数及其应用
5.1.1变化率问题
学习目标
通过任务一的学习,学会运用运动变化的观点和数形结合的思想解决数学问题,经历平均速度到瞬时速度的逼近过程,体会极限的思想。
通过任务二的学习,进一步体会运动变化的观点和数形结合思想在数学中的应用,经历割线到切线的逼近过程,加深对极限思想的认识,提升学生的数学抽象、直观想象和数学运算的核心素养
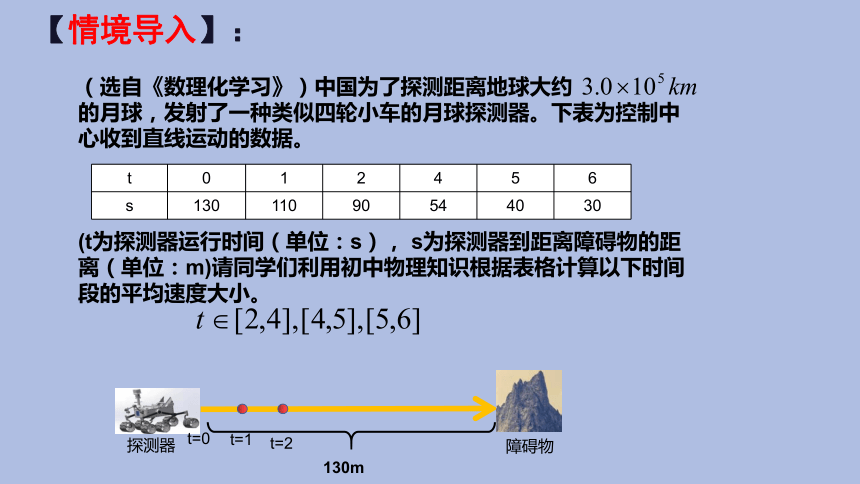
【情境导入】:
(选自《数理化学习》)中国为了探测距离地球大约 的月球,发射了一种类似四轮小车的月球探测器。下表为控制中心收到直线运动的数据。
(t为探测器运行时间(单位:s), s为探测器到距离障碍物的距离(单位:m)请同学们利用初中物理知识根据表格计算以下时间段的平均速度大小。
t 0 1 2 4 5 6
s 130 110 90 54 40 30
130m
障碍物
探测器
t=0
t=1
t=2
平均速度:
平均速度是物体在某段时间内的位移与所用时间的比值,一个描述物体运动平均快慢程度和运动方向的矢量,它粗略地表示物体在一个时间段内的运动情况.
瞬时速度:
我们把物体在某一时刻的速度称为瞬时速度。
在物理中,做变速运动的物体在不同的时刻,速度是不同的,
平均速度公式:物体在做直线运动时经过了A位置和B位置 . 若运动的位移与时间的关系为s(t),则从tA到tB这段时间内的平均速度是多少?
预备知识:
微课再回首:
[t0,t0+△t]平均速度与t0时刻瞬时速度有什么区别和联系
思考:
问题1:如何寻找t=1时刻附近的小时间段?
问题2:瞬时速度如何计算?
【合作探究】:
任务一:求变速直线运动S(t)=t2在t=1时刻的瞬时速度
思考下列问题,小组讨论,给出问题的解决方案。
时间段 平均 速度 时间段 平均
速度
-0.01 [0.99,1] 0.01 [1,1.01]
-0.001 [0.999,1] 0.001 [1,1.001]
-0.0001 [0.9999,1] 1.9999 0.0001 [1,1.0001] 2.0001
-0.00001 [0.99999,1] 1.99999 0.00001 [1,1.00001] 2.00001
.......................... ....................................
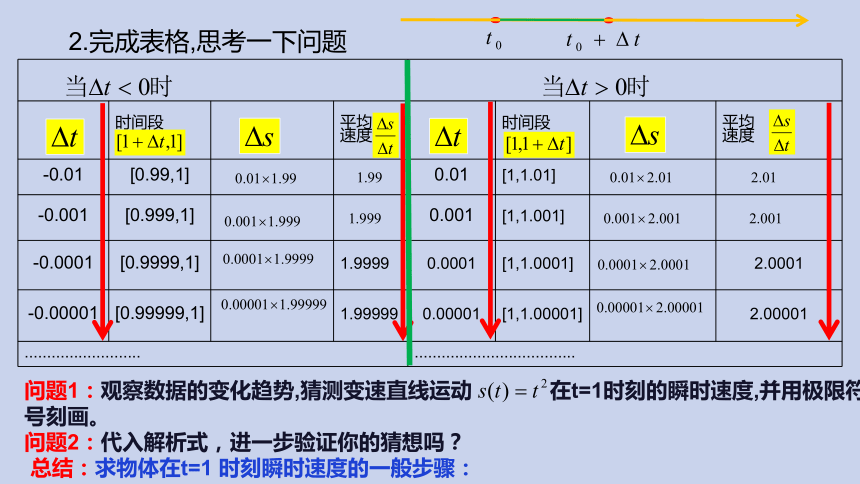
2.完成表格,思考一下问题
问题1:观察数据的变化趋势,猜测变速直线运动 在t=1时刻的瞬时速度,并用极限符号刻画。
问题2:代入解析式,进一步验证你的猜想吗?
总结:求物体在t=1 时刻瞬时速度的一般步骤:
【学习新知】:
答案:
变式:
(1)求变速直线运动 在t=2s时的瞬时速度;
(2)归纳变速直线运动s(t)在 某一时刻t=t0的瞬时速度?
【强化训练】:
一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系:
求运动员在t=1s时的瞬时速度?
【强化训练】:
一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系:
求运动员在t=1s时的瞬时速度?
【微课小测验】:
【探索新知】:
思考:
1. 上述抛物线在P(1,1)的切线如何定义?
2. 动手折纸,体会 的变化趋势,回答割线斜率与切线斜率之间的关系。
用极限符号刻画。
思考:
展示:
任务二:如何求抛物线f(x)=x2在P(1,1)处的切线斜率?
平均 速度 平均
速度
-0.01 1.99 0.01 2.01
-0.001 1.999 0.001 2.001
-0.0001 1.9999 0.0001 2.0001
-0.00001 1.99999 0.00001 2.00001
............. ..................... 割线斜率 割线斜率
-0.01 1.99 0.01 2.01
-0.001 1.999 0.001 2.001
-0.0001 1.9999 0.0001 2.0001
-0.00001 1.99999 0.00001 2.00001
............. ..................... 问题再思考:
A
B
变化率问题在本单元的主题地位:
切线的斜率
导数的概念
函数的最值
导数的正负
(函数的单调性)
割线斜率
平均速度
瞬时速度
【课堂小结】:
1.本节课所学知识点?
2.本节课所用到的数学思想和方法?
极限思想 ; 数形结合
平均速度的极限就是瞬时速度
割线斜率的极限就是切线斜率
对于函数关系式 在 时刻的瞬时速度
对于函数关系式 在 的切线斜率
一、两个思想:
二、两个关系:
三、两个结论:
四、三个核心素养:
数学抽象 ; 直观想象;数学运算
第五章一元函数的导数及其应用
5.1.1变化率问题
学习目标
通过任务一的学习,学会运用运动变化的观点和数形结合的思想解决数学问题,经历平均速度到瞬时速度的逼近过程,体会极限的思想。
通过任务二的学习,进一步体会运动变化的观点和数形结合思想在数学中的应用,经历割线到切线的逼近过程,加深对极限思想的认识,提升学生的数学抽象、直观想象和数学运算的核心素养
【情境导入】:
(选自《数理化学习》)中国为了探测距离地球大约 的月球,发射了一种类似四轮小车的月球探测器。下表为控制中心收到直线运动的数据。
(t为探测器运行时间(单位:s), s为探测器到距离障碍物的距离(单位:m)请同学们利用初中物理知识根据表格计算以下时间段的平均速度大小。
t 0 1 2 4 5 6
s 130 110 90 54 40 30
130m
障碍物
探测器
t=0
t=1
t=2
平均速度:
平均速度是物体在某段时间内的位移与所用时间的比值,一个描述物体运动平均快慢程度和运动方向的矢量,它粗略地表示物体在一个时间段内的运动情况.
瞬时速度:
我们把物体在某一时刻的速度称为瞬时速度。
在物理中,做变速运动的物体在不同的时刻,速度是不同的,
平均速度公式:物体在做直线运动时经过了A位置和B位置 . 若运动的位移与时间的关系为s(t),则从tA到tB这段时间内的平均速度是多少?
预备知识:
微课再回首:
[t0,t0+△t]平均速度与t0时刻瞬时速度有什么区别和联系
思考:
问题1:如何寻找t=1时刻附近的小时间段?
问题2:瞬时速度如何计算?
【合作探究】:
任务一:求变速直线运动S(t)=t2在t=1时刻的瞬时速度
思考下列问题,小组讨论,给出问题的解决方案。
时间段 平均 速度 时间段 平均
速度
-0.01 [0.99,1] 0.01 [1,1.01]
-0.001 [0.999,1] 0.001 [1,1.001]
-0.0001 [0.9999,1] 1.9999 0.0001 [1,1.0001] 2.0001
-0.00001 [0.99999,1] 1.99999 0.00001 [1,1.00001] 2.00001
.......................... ....................................
2.完成表格,思考一下问题
问题1:观察数据的变化趋势,猜测变速直线运动 在t=1时刻的瞬时速度,并用极限符号刻画。
问题2:代入解析式,进一步验证你的猜想吗?
总结:求物体在t=1 时刻瞬时速度的一般步骤:
【学习新知】:
答案:
变式:
(1)求变速直线运动 在t=2s时的瞬时速度;
(2)归纳变速直线运动s(t)在 某一时刻t=t0的瞬时速度?
【强化训练】:
一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系:
求运动员在t=1s时的瞬时速度?
【强化训练】:
一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系:
求运动员在t=1s时的瞬时速度?
【微课小测验】:
【探索新知】:
思考:
1. 上述抛物线在P(1,1)的切线如何定义?
2. 动手折纸,体会 的变化趋势,回答割线斜率与切线斜率之间的关系。
用极限符号刻画。
思考:
展示:
任务二:如何求抛物线f(x)=x2在P(1,1)处的切线斜率?
平均 速度 平均
速度
-0.01 1.99 0.01 2.01
-0.001 1.999 0.001 2.001
-0.0001 1.9999 0.0001 2.0001
-0.00001 1.99999 0.00001 2.00001
............. ..................... 割线斜率 割线斜率
-0.01 1.99 0.01 2.01
-0.001 1.999 0.001 2.001
-0.0001 1.9999 0.0001 2.0001
-0.00001 1.99999 0.00001 2.00001
............. ..................... 问题再思考:
A
B
变化率问题在本单元的主题地位:
切线的斜率
导数的概念
函数的最值
导数的正负
(函数的单调性)
割线斜率
平均速度
瞬时速度
【课堂小结】:
1.本节课所学知识点?
2.本节课所用到的数学思想和方法?
极限思想 ; 数形结合
平均速度的极限就是瞬时速度
割线斜率的极限就是切线斜率
对于函数关系式 在 时刻的瞬时速度
对于函数关系式 在 的切线斜率
一、两个思想:
二、两个关系:
三、两个结论:
四、三个核心素养:
数学抽象 ; 直观想象;数学运算
