2016湖南高考数学二轮备考函数、导数及其应用专题复习策略探讨
文档属性
| 名称 | 2016湖南高考数学二轮备考函数、导数及其应用专题复习策略探讨 |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-20 20:10:28 | ||
图片预览








文档简介
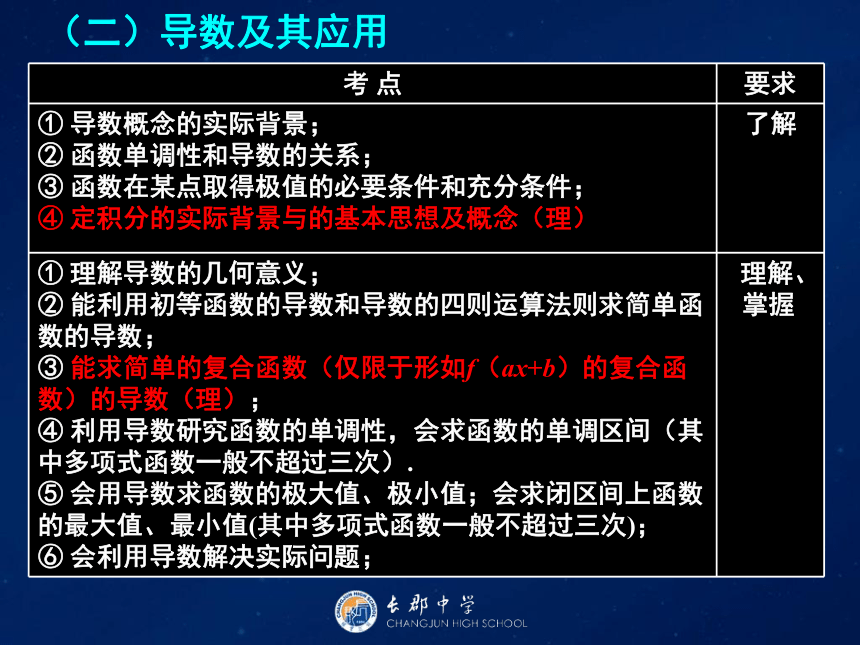
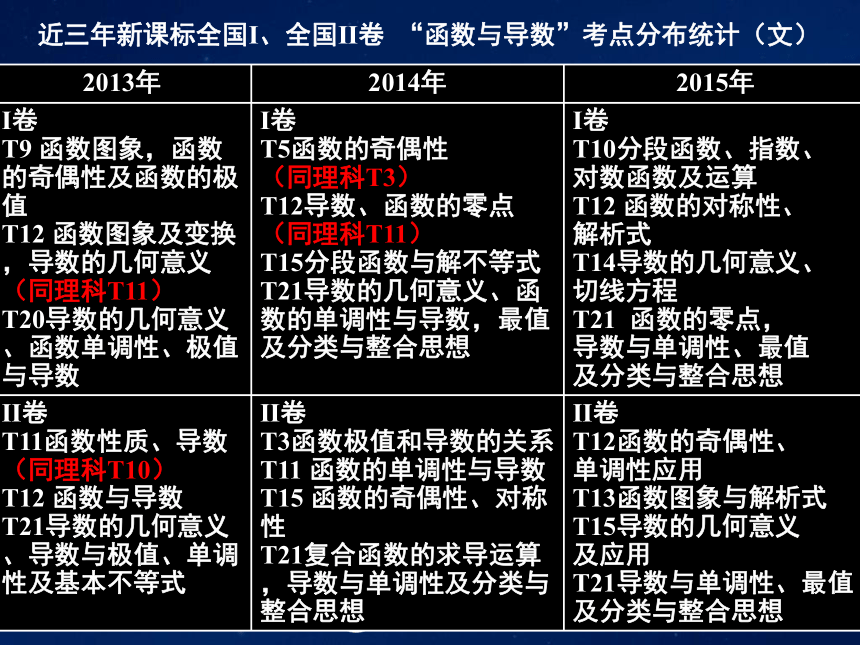
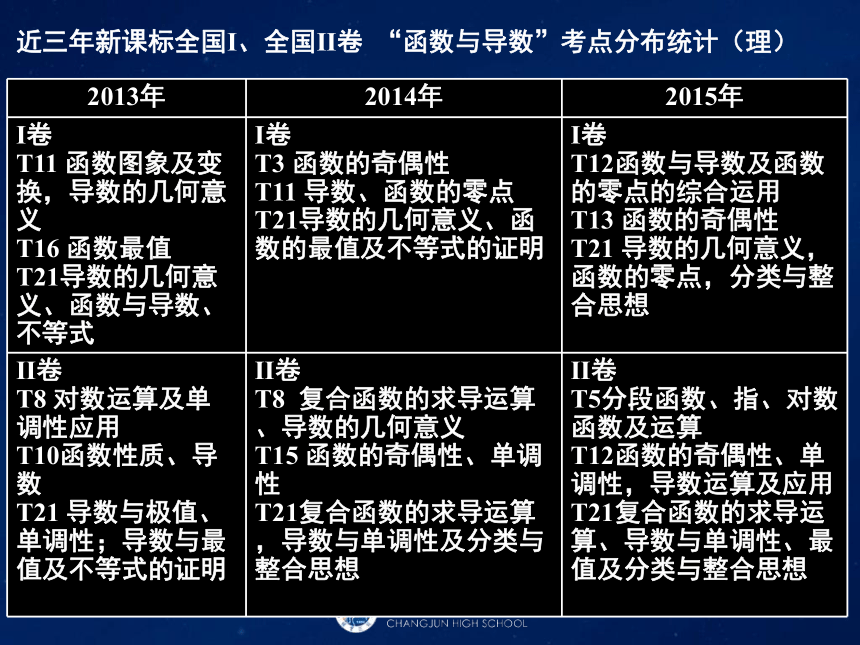
课件64张PPT。一、【考纲要求】 (解读考纲,把握方向)(一)函数的概念与基本初等函数(Ⅰ)(二)导数及其应用二、【考情分析】(预测考点,心中有数)1、考点统计 近三年新课标全国Ⅰ、全国Ⅱ卷 “函数与导数”考点分布统计(文) 近三年新课标全国Ⅰ、全国Ⅱ卷 “函数与导数”考点分布统计(理) 2、命题规律 新课标全国卷对“函数与导数”的考查,比较稳定。基本格局为:文科“三小一大”,分值27分;理科“两小一大”,分值22分。小题主要考查:函数的单调性、奇偶性、函数的零点、导数的几何意义、函数的极值与最值、函数的图象及变换、数形结合思想等,试题难度一般是:文科一道容易题,一道中档题,一道压轴题;理科一道中档题,一道压轴题;大题则在考查函数与导数的基础时,注重考查函数与方程、化归与转化、分类与整合等数学思想方法,还综合考查了运算求解能力、推理论证能力、抽象概括能力等,几乎作为压轴题,难度较大。 三、【题型归类】(考点突破,形成能力)类型一:函数的概念、图象和性质 1.(2015年新课标Ⅰ卷理科第13题)若函数f(x)=xln(x+ )为偶函数,则a=_____________.1 2.(2014年新课标Ⅰ卷理科第3题,文科第5题)设函数的f(x),g(x)定义域为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
A. f(x)g(x)是偶函数
B. |f(x)|g(x)是奇函数
C. f(x)|g(x)|是奇函数
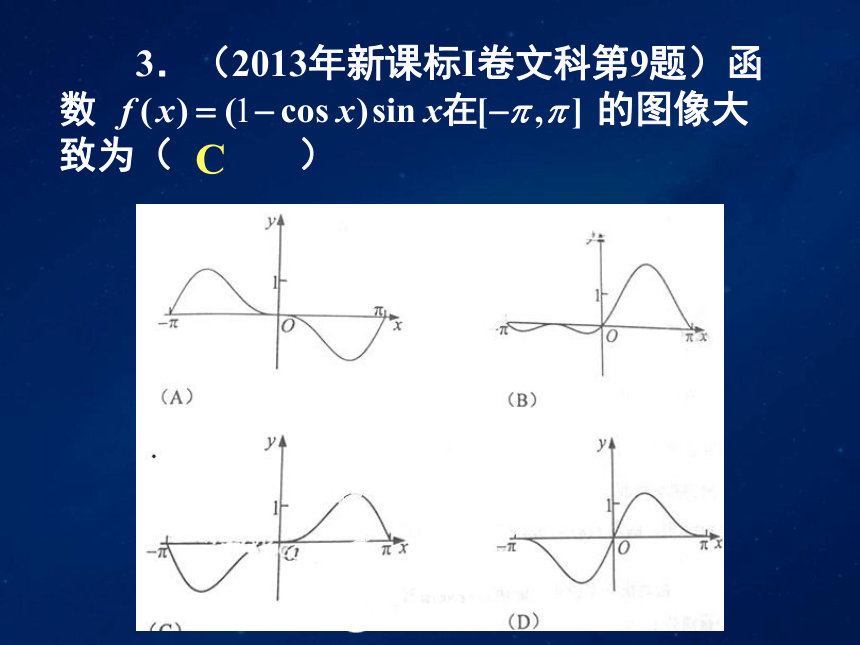
D. |f(x)g(x)|是奇函数C 3.(2013年新课标Ⅰ卷文科第9题)函数 的图像大致为( ) C 4.(2014年新课标Ⅱ卷文科第15题) 偶函数y=f(x)的图像关于x=2直线对称,f(3)=3,则f(-1)=________.3类型二:分段函数、复合函数ACC类型三:利用导数的几何意义处理切线方程问题b=1D类型四:利用导数讨论函数的单调性问题 AD类型五:函数的极值与最值问题BC 类型六:利用导数研究方程的根(函数的零点)问题C类型七:导数与不等式的综合问题(一)函数不等式的证明问题
利用函数与导数证明不等式是新课标高考的命题热点之一,既考查函数的单调性、极值、最值等基础知识,同时考查转化与化归、分类与整合、函数与方程等思想方法,又综合考查求解运算能力、推理论证能力,此类问题应予以关注。【解析】 (1)略【点评】
1、函数不等式的证明通常是采用构造函数,转化为利用导数研究函数的单调性、极值或最值问题。关键是能够根据题设恰当转化,合理构造,优化思维。2、在此类题型中,关注两个问题:
(1)从不同角度看问题,转化与化归可否有不同的解题途径,找寻更佳思路。如思路二构造为整式函数比思路一中的分式函数要简洁的多。
(2)该类问题几乎是涉及多元问题,如何成功实施减元(换元或整体处理等)化归为一元进行求解。 3、在此类函数与方程综合问题中,求证零点“ ”的两种常用处理方法:
①利用等式“ ”,将x1,x2整体变元,再构造函数解决;
②利用原函数f(x)的单调性,转化为证 (或 ,再利用 ,转化为“ ”的问题.【考题链接】(二)含参数不等式的恒成立或有解问题 C D B【解析】法一:分类讨论(略)【点评】
1.不等式“恒成立”或“有解”求解的常用方法:
(1)最值法(有时先要分离变量可简化运算,如题1);
(2)图象法(如题2、题3)
2.方程根的问题:可化为研究相应函数的图象,而图象又归结为极值点和单调区间的讨论 类型八:导数与数列的综合问题考点:
1.利用导数研究函数的单调性;
2.利用数学归纳法证明数列不等式.
3.分类与整合思想、一般与特殊思想【点评】
1.利用导数研究函数的单调性;
2.利用数学归纳法证明数列不等式.
3.合理恰当进行放缩,达到目标不等式【考题链接】四、【备考策略】(主干整合,归纳扩展)1、强基础
抓好两条主线,构建函数知识网络。一是“基本函数的概念与性质”,熟练掌握函数的定义域、解析式、值域、奇偶性、单调性、周期性、对称性等基本知识及求解方法,并会灵活应用;二是“基本函数的图象与性质”,要熟练掌握一次函数、二次函数、反比例函数、指数函数、对数函数等常用函数的图象以及图象变换,会运用基本初等函数的图像分析函数的性质,会利用导数破解图象的特征、研究方程根(函数的零点)及其性质。2、重能力
从对近几年全国卷函数与导数的高考试题分析,充分体现高考命题强调 “以能力力意”的指导思想,全国高考对函数与导数的考查重在对函数与导数知识理解的准确性、深刻性,综合考查能用函数与方程思想、转化与化归思想、分类与整合思想,还综合考查运算求解能力、推理论证能力、抽象概括能力,并且是多种能力同时考查。因此,在对“函数与导数”二轮复习中,既要突出基础性,还要关注综合性,对中上学生(尤其是尖子生)强化思想方法的训练,要善于转化命题,引进变量构建函数,形成透过函数看问题的意识;加强训练学生“增加条件”,合理恰当分类;强化“由式到图”和“由图到式”的转化训练;关注学生的运算能力的训练,培养学生合理、准确的运算能力;注重数学思维能力的训练, 在审题中能抓住思维起点,结合有关知识能够合乎逻辑地准确表述推理过程,训练推理论证能力。3、研考题
历届高考真题是考试大纲中的考试内容和考试要求的具体落实和体现,通过纵、横两向对高考真题的研究,吸纳其中数学精神的本质,贯穿于后段的复习之中。才能更好地把握考纲要求,考题的重点、热点;摸准方向,少走弯路,提高效率。4、抓落实
在“函数与导数”复习中,要准确理解概念、掌握通性通法,特别关注一些易错点,切实抓好落实。
易错点主要有:
①求导公式使用不正确,切线方程表达错误 ;
② 忽视函数的定义域,单调区间书写不规范;
③ 用几何直观代替证明,而没有严格的逻辑推理;
④ 构造函数不当,造成运算繁杂;
⑤ 不知怎样分类讨论;
⑥ 缺少特殊化解决问题的策略;
⑦ 片面地、孤立地考略问题,不能联系前后问进行难点突破对策:
①提高求导运算的准确性,特别是含有复合函数的求导和分式型函数的求导;
② 注重分类讨论问题中,寻找分类依据的训练,做到不重不漏;
③ 数形结合,以“形”引导思维,寻找解题的途径;
④ 加强代数推理能力,严谨、合理的数学表述的培养;
⑤ 合理地对问题进行转化,抓住问题的质;
⑥ 强化一般与特殊转化的针对训练
A. f(x)g(x)是偶函数
B. |f(x)|g(x)是奇函数
C. f(x)|g(x)|是奇函数
D. |f(x)g(x)|是奇函数C 3.(2013年新课标Ⅰ卷文科第9题)函数 的图像大致为( ) C 4.(2014年新课标Ⅱ卷文科第15题) 偶函数y=f(x)的图像关于x=2直线对称,f(3)=3,则f(-1)=________.3类型二:分段函数、复合函数ACC类型三:利用导数的几何意义处理切线方程问题b=1D类型四:利用导数讨论函数的单调性问题 AD类型五:函数的极值与最值问题BC 类型六:利用导数研究方程的根(函数的零点)问题C类型七:导数与不等式的综合问题(一)函数不等式的证明问题
利用函数与导数证明不等式是新课标高考的命题热点之一,既考查函数的单调性、极值、最值等基础知识,同时考查转化与化归、分类与整合、函数与方程等思想方法,又综合考查求解运算能力、推理论证能力,此类问题应予以关注。【解析】 (1)略【点评】
1、函数不等式的证明通常是采用构造函数,转化为利用导数研究函数的单调性、极值或最值问题。关键是能够根据题设恰当转化,合理构造,优化思维。2、在此类题型中,关注两个问题:
(1)从不同角度看问题,转化与化归可否有不同的解题途径,找寻更佳思路。如思路二构造为整式函数比思路一中的分式函数要简洁的多。
(2)该类问题几乎是涉及多元问题,如何成功实施减元(换元或整体处理等)化归为一元进行求解。 3、在此类函数与方程综合问题中,求证零点“ ”的两种常用处理方法:
①利用等式“ ”,将x1,x2整体变元,再构造函数解决;
②利用原函数f(x)的单调性,转化为证 (或 ,再利用 ,转化为“ ”的问题.【考题链接】(二)含参数不等式的恒成立或有解问题 C D B【解析】法一:分类讨论(略)【点评】
1.不等式“恒成立”或“有解”求解的常用方法:
(1)最值法(有时先要分离变量可简化运算,如题1);
(2)图象法(如题2、题3)
2.方程根的问题:可化为研究相应函数的图象,而图象又归结为极值点和单调区间的讨论 类型八:导数与数列的综合问题考点:
1.利用导数研究函数的单调性;
2.利用数学归纳法证明数列不等式.
3.分类与整合思想、一般与特殊思想【点评】
1.利用导数研究函数的单调性;
2.利用数学归纳法证明数列不等式.
3.合理恰当进行放缩,达到目标不等式【考题链接】四、【备考策略】(主干整合,归纳扩展)1、强基础
抓好两条主线,构建函数知识网络。一是“基本函数的概念与性质”,熟练掌握函数的定义域、解析式、值域、奇偶性、单调性、周期性、对称性等基本知识及求解方法,并会灵活应用;二是“基本函数的图象与性质”,要熟练掌握一次函数、二次函数、反比例函数、指数函数、对数函数等常用函数的图象以及图象变换,会运用基本初等函数的图像分析函数的性质,会利用导数破解图象的特征、研究方程根(函数的零点)及其性质。2、重能力
从对近几年全国卷函数与导数的高考试题分析,充分体现高考命题强调 “以能力力意”的指导思想,全国高考对函数与导数的考查重在对函数与导数知识理解的准确性、深刻性,综合考查能用函数与方程思想、转化与化归思想、分类与整合思想,还综合考查运算求解能力、推理论证能力、抽象概括能力,并且是多种能力同时考查。因此,在对“函数与导数”二轮复习中,既要突出基础性,还要关注综合性,对中上学生(尤其是尖子生)强化思想方法的训练,要善于转化命题,引进变量构建函数,形成透过函数看问题的意识;加强训练学生“增加条件”,合理恰当分类;强化“由式到图”和“由图到式”的转化训练;关注学生的运算能力的训练,培养学生合理、准确的运算能力;注重数学思维能力的训练, 在审题中能抓住思维起点,结合有关知识能够合乎逻辑地准确表述推理过程,训练推理论证能力。3、研考题
历届高考真题是考试大纲中的考试内容和考试要求的具体落实和体现,通过纵、横两向对高考真题的研究,吸纳其中数学精神的本质,贯穿于后段的复习之中。才能更好地把握考纲要求,考题的重点、热点;摸准方向,少走弯路,提高效率。4、抓落实
在“函数与导数”复习中,要准确理解概念、掌握通性通法,特别关注一些易错点,切实抓好落实。
易错点主要有:
①求导公式使用不正确,切线方程表达错误 ;
② 忽视函数的定义域,单调区间书写不规范;
③ 用几何直观代替证明,而没有严格的逻辑推理;
④ 构造函数不当,造成运算繁杂;
⑤ 不知怎样分类讨论;
⑥ 缺少特殊化解决问题的策略;
⑦ 片面地、孤立地考略问题,不能联系前后问进行难点突破对策:
①提高求导运算的准确性,特别是含有复合函数的求导和分式型函数的求导;
② 注重分类讨论问题中,寻找分类依据的训练,做到不重不漏;
③ 数形结合,以“形”引导思维,寻找解题的途径;
④ 加强代数推理能力,严谨、合理的数学表述的培养;
⑤ 合理地对问题进行转化,抓住问题的质;
⑥ 强化一般与特殊转化的针对训练
同课章节目录
