2024-2025学年八年级下学期数学(浙教版)开学摸底考试(含答案)
文档属性
| 名称 | 2024-2025学年八年级下学期数学(浙教版)开学摸底考试(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-15 21:24:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
保密★启用前
20224-2025学年八年级下册开学摸底考试(浙教版)
数学
考试范围:八上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本大题有10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在下列图形中, 是轴对称图形有 ( ) 个
A.1 B.2 C.3 D.4
2.某农户买黄金瓜,第一天上午买了45斤,价格为每斤x元,下午他又买了35斤,价格为每斤y元.第二天他以每斤元的价格卖完了80斤,结果同第一天比发现自己亏了.其原因是( )
A. B. C. D.
3.象棋在中国有着三千多年的历史,如图是一方的棋盘,如果“帅”的坐标是(1,1),“卒”的坐标是(3,2),那么“马”的坐标是( )
A. B. C. D.
4.一次函数中,随的增大而增大,且,则这个函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,,,点、在上,那么添加下列一个条件后,仍无法判断的是( )
A. B. C. D.
6.下列命题的逆命题是真命题的是( )
A.直角三角形的两个锐角互余 B.对顶角相等
C.全等三角形的面积相等 D.全等三角形的对应角相等
7.若点A到x轴的距离是5,到y轴的距离是4,且点A在第二象限,则A的坐标为( ).
A. B. C. D.
8.对于一次函数,下列结论错误的是( )
A.函数图象与轴的交点坐标是
B.函数值随自变量的增大而减小
C.函数图象不经过第三象限
D.函数图象向下平移4个单位长度得的图象
9.如图,AB=4,动点P满足S△PAB=4,则PA+PB的最小值为( )
A.5 B. C. D.
10.已知菱形ABCD,E、F是动点,边长为5,,,则下列结论①;②为等边三角形;③;④若,则,正确的有几个( )
A.1 B.2 C.3 D.4
二、填空题(本大题有6小题,每小题3分,共18分)
11.关于x的不等式的最小整数解是 .
12.已知y是关于x的一次函数,下表列出了部分对应值,则m的值是 .
x 0 1 2
y 1 m 5
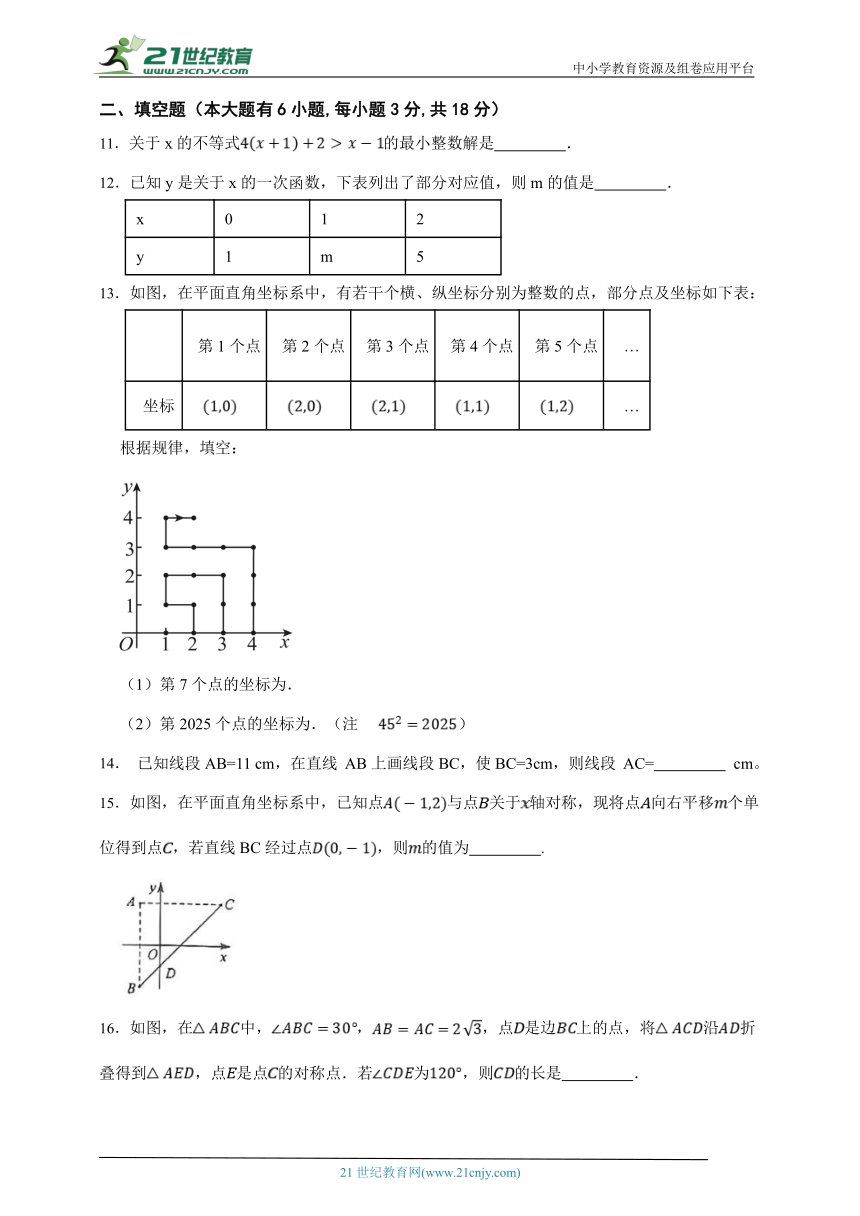
13.如图,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,部分点及坐标如下表:
第1个点 第2个点 第3个点 第4个点 第5个点 …
坐标 …
根据规律,填空:
(1)第7个点的坐标为.
(2)第2025个点的坐标为.(注)
14. 已知线段AB=11 cm,在直线 AB上画线段BC,使BC=3cm,则线段 AC= cm。
15.如图,在平面直角坐标系中,已知点与点关于轴对称,现将点向右平移个单位得到点,若直线BC经过点,则的值为 .
16.如图,在中,,,点是边上的点,将沿折叠得到,点是点的对称点.若为,则的长是 .
三、解答题(本题有8小题,共72分.解答应写出必要的文字说明,证明过程或演算步骤)
17.(1)计算:
(2)下面是小明同学解不等式的过程,请认真阅读并完成相应任务.
解:……第一步
……第二步
……第三步
……第四步
……第五步
任务一:填空:①以上解题过程中,第二步是依据_________(运算律)进行变形的;
②第_________步开始出现错误,这一步错误的原因是_________;
任务二:请直接写出该不等式的正确解集.
18.如图所示,在△ABC中,AB=AC,∠1=∠2,AD⊥CD于点D,AE⊥BE于点E,BE,CD交于点O.
求证:(1)△ABE≌△ACD;
(2)OD=OE.
19.如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,2).
(1)填空:点A关于x轴对称的点的坐标是 ,点B关于y轴对称的点的坐标是 ;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到.请写出的三个顶点坐标;
(3)求△ABC的面积.
20.如图,在 ABC中AD、AE、AF分别为△ABC的高、角平分线和中线,已知 AFC的面积为10,AD=4,∠DAE=20°,∠C=30°.
(1)求BC的长度;
(2)求∠B的度数.
21.一次函数的图象经过,两点.
(1)求此函数的表达式.
(2)试判断点是否在此函数的图象上,并说明理由.
22.倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出A型和B型两款垃圾分拣机器人,已知2台A型机器人和5台B型机器人同时工作2小时共分拣垃圾3.6吨,3台A型机器人和2台B型机器人同时工作5小时共分拣垃圾8吨.
(1)1台A型机器人和1台B型机器人每小时各分拣垃圾多少吨?
(2)某垃圾处理厂计划向机器人公司购进一批A型和B型垃圾分拣机器人,机器人公司的报价如下表:
型号 原价 购买量少于30台 购买量不少于30台
A型 20万元/台 原价购买 打九折
B型 12万元/台 原价购买 打八折
①若要求这批机器人每小时一共能分拣垃圾20吨.设其中购买A型机器人x台(10≤x≤35),购买两种机器人总费用为W万元.求W与x的函数关系式,并说明如何购买总费用最少;
②为了加快垃圾分拣速度,垃圾处理厂计划用不超过140万元增购这两种机器人共10台,机器人公司全部以打折后价格销售,这10台机器人每小时最多处理多少吨垃圾?
23.如图,△ABC的两顶点分别为B(0,0),C(4,0),顶点A在直线l:y=-x+3上.
(1)当△ABC是以BC为底的等腰三角形时,求点A的坐标;
(2)当△ABC的面积为4时,求点A的坐标;
(3)在直线l上是否存在点A,使∠BAC=90°?若存在,求出点A的坐标;若不存在请说明理由.
24.如图是“赵爽弦图”,其中、、和是四个全等的直角三角形,四边形和都是正方形,根据这个图形的面积关系,可以证明勾股定理设,,,取,.
(1)求四个直角三角形的面积和;
(2)求的值.
答案解析部分
1.C
解:第一、第二、第四个图形都能找到这样的一条直线,使这些图形沿着一条直线对折后两部分完全重合,所以是轴对称图形,
第三个图形找到这样的一条直线,使这个图形沿着一条直线对折后两部分完全重合,所以不是轴对称图形,
所以是轴对称图形有3个.
故答案为:C.
利用轴对称图形的定义(如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴)逐项分析判断即可.
2.B
3.C
解:如图所示,建立平面直角坐标系,在“马"的坐标是(-1,2),
故答案为:C.
本题考查建立平面直角坐标系。根据题中所给点的坐标,确定原点和坐标轴即可。
4.B
解: 一次函数中,随的增大而增大,且,
则 k>0,b<0
则一次函数过第一、三、四象限,不过第二象限。
故答案为:B.
本题考查一次函数的性质和象限。当k>0,b>0时,一次函数y=kx+b(k≠0)过第一、二、三象限;当k>0,b<0时,一次函数y=kx+b(k≠0)过第一、三、四象限;当k<0,b>0时,一次函数y=kx+b(k≠0)过第一、二、四象限;当k<0,b<0时,一次函数y=kx+b(k≠0)过第二、三、四象限。熟练掌握一次函数的性质很关键。
5.D
6.A
解:A、逆命题是:两个锐角互余的三角形是直角三角三角形,是真命题,故此选项正确,符合题意;
B、逆命题是:相等的角是对顶角,是假命题,故此选项错误,不符合题意;
C、逆命题是:三个角对应相等的两个三角形全等,是假命题,故此选项错误,不符合题意;
D、逆命题是:面积相等的三角形是全等三角形,是假命题,故此选项错误,不符合题意.
故答案为:A.
先写出命题的逆命题,再判断真假即可求解.
7.B
8.A
解:A、一次函数y=-x+4中,令y=0,得-x+4=0,解得x=4,所以该一次函数图象与x轴的交点坐标为(4,0),故此选项错误,符合题意;
B、一次函数y=-x+4中,自变量的系数k=-1<0,所以数值随自变量的增大而减小,故此选项正确,不符合题意;
C、一次函数y=-x+4中,自变量的系数k=-1<0,所以函数图象经过第二、四象限;一次函数y=-x+4中,常数项b=4>0,所以图象交y轴的正半轴,所以该函数图象经过一、二、四象限,即函数图象不经过第三象限,故此选项正确,不符合题意;
D、一次函数y=-x+4中,向下平移4个单位长度后的函数解析式为y=-x+4-4=-x,故此选项正确,不符合题意.
故答案为:A.
令一次函数解析式中的y=0算出对应的自变量x的值,即可得出该函数图象与x轴交点的坐标,据此可判断A选项;
一次函数y=ax+b(a≠0),当a>0时,函数值随自变量的增大而增大,当a<0时,函数值随自变量的增大而减小,据此可判断B选项;
一次函数y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象限;当a>0,b<0时,图象过一、三、四象限;当a>0,b=0时,图象过一、三象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限,当a<0,b=0时,图象过二、四象限,据此可判断C选项;
一次函数y=ax+b(a≠0)图象的平移规律是“左移加,右移减;上移加,下移减”,据此可判断D选项.
9.D
解:由题意,△PAB的高为4×2÷4=2,则P点在与AB平行且距离AB为2的直线l上,
如图,作A关于直线l对称点A',连接A'B,A'P,
则PA'=PA,PA+PB=PA'+PB≥A'B,A'B即为所求最小值,
Rt△A'AB中,A'A=2×2=4,AB=4,则A'B=
故答案为:D.
先算出三角形的高,得到P点在与AB平行且距离AB为2的直线l上,作A关于直线l对称点A',则A'B即为所求最小值,利用勾股定理求解即可.
10.D
解:①四边形是菱形,∠BAD=120°,
∴AB=BC,AD∥BC,,
,
∴∠B=∠CAF=60°,
∴是等边三角形,
∴BC=AC,
在和中,
,
∴,故①正确;
②∵,
,,
∵是等边三角形,
∴∠ACB=∠BCE+∠ACE=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=∠ECF=60°,
∴是等边三角形,故②正确;
③∵是等边三角形,
∴∠CFG=60°,
,,
,故③正确;
④如图,过点作EM//BC交于点,
易证是等边三角形,则,
∵AF//EM,
∴,故④正确,
故答案为:D.
①根据菱形的性质、平行线的性质证出AB=BC,∠B=∠CAF=60°,从而利用“SAS”可得,即可判断该结论正确;②由,得,,根据等边三角形的性质得∠ACB=∠BCE+∠ACE=60°,进行等量代换得∠ACF+∠ACE=∠ECF=60°,从而证出是等边三角形,即可判断该结论正确正确;③由等边三角形的性质、外角的性质得,即可判断该结论正确;④过点作EM//BC交下点点,易证是等边三角形,则,由AF//EM,则,即可判断该结论正确.
11.
12.3
13.,
14.8或14
解:分两种情况讨论:
①如图,当点C在线段上,
,,
;
②如图,当点C在线段的延长线上,
,,
,
综上可知,线段的长为或,
故答案为:或.
分两种情况讨论:①点C在线段上;②点C在线段的延长线上,分别求解即可得到答案.
15.4
解:∵ 点与点关于轴对称,
∴B(-1,-2),
设直线BC解析式为y=kx+b,
把B(-1,-2)代入解析式得,解得k=1,b=-1,
∴直线BC:y=x-1,
将点向右平移个单位得到点 ,则C(-1+m,2),
把点C坐标代入y=x-1中,得-1+m-1=2,
解得m=4.
故答案为:4.
先求出B坐标,再利用待定系数法求出直线BC解析式,由坐标的平移求C(-1+m,2),然后把点C坐标代入直线BC解析式即可求出m值.
16.2或4
解:作于点,
∵,,
∴,
∴,
∴,
当点在直线的下方时,如图,
由折叠的性质得,
∵,
∴,
∴,
∴,,
∴,,
∴;
当点在直线的上方时,如图,
∵,
∴,
∴,,
∴,,
∴,
∴.
综上,的长是2或4.
故答案为:2或4.
先根据30°角的直角三角形的性质得到,然后分两种情况讨论,利用等腰三角形的性质以及含30度角的直角三角形的性质即可解题.
17.(1);(2)任务一:①乘法分配律;②五,不等式两边都除以,不等号的方向没有改变;任务二:
18.证明:(1)∵AD⊥DC,AE⊥BE,
∴∠ADC=∠AEB=90°,
∵∠1=∠2,∠EAB=∠1+∠DAE,∠DAC=∠2+∠DAE,
∴∠DAC=∠EAB,
在与中,
,
∴;
(2)连接AO,如图,
∵,
∴AE=AD,
在和中,
,
∴,
∴OD=OE.
(1)根据垂直的定义得∠ADC=∠AEB=90°,然后根据角的和差关系得∠DAC=∠EAB,接下来由”AAS“即可得证结论;
(2)根据全等三角形对应边相等的性质得AE=AD,然后得证,于是根据全等三角形对应边相等即可得证结论.
19.(1)(2,1),(-4,3);(2)(0,0),(2,4),(-1,3);(3)5.
20.(1)解:∵AF是△ABC的中线,
∴BC=2BF=2CF,BF=CF,
∴△ABF和△ACF的面积相等,
∵△AFC的面积为10,
∴∠ABF的面积为10,
∵AD=4,
∴ =10,
∴BF=5,
∴BC=2BF=10;
(2)解:∵AD是△ABC的高,
∴∠ADC=90°,
∵∠DAE=20°,
∴∠AED=180°﹣90°﹣20°=70°,
∵∠C=30°,
∴∠CAE=∠AED﹣∠C=40°,
∵AE是△ABC的角平分线,
∴∠BAC=2∠CAE=80°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣80°﹣30°=70°.
(1)求出△ABF和△ACF的面积相等,根据三角形的面积求出BF,继而求出BC即可;
(2)求出∠AED的度数,根据三角形的外角的性质求出∠CAE,根据角平分线的含义求出∠BAC,继而由三角形的内角和定理求出∠B即可。
21.(1)解:设一次函数的解析式为,
一次函数的图象经过,两点,
,
解得,
此函数的表达式为;
(2)解:点不在此函数的图象上,
理由:把代入中得,,
点不在此函数的图象上.
(1)设一次函数解析式为y=kx+b,然后将M和N的坐标分别代入,构建方程组求出k和b的值,即用待定系数法求解即可;
(2)利用(1)中的解析式,通过计算自变量为3对应的函数值可判断点P是否在此函数的图象上。
22.(1)1台A型机器人每小时分拣0.4吨,1台B型机器人每小时分拣0.2吨;(2)①,购买A型35台,B型30台总费用最少;②3吨垃圾.
23.(1)解:如图,当△ABC是以BC为底的等腰三角形时,点A在BC的中垂线上.
∵B(0,0),C(4,0),
∴BC的中垂线为x=2.
又点A在直线l:y=-x+3上,
∴y=-×2+3=2,
即A(2,2);
(2)解:设A(a,b).则依题意得
BC·|b|=4,即×4|b|=4,
解得|b|=2
∴b=±2.
①当b=2时,2=-a+3,
解得 a=2
则A(2,2);
②当b=-2时,-2=-a+3,
解得 a=10
则A(10,-2).
综上所述,点A的坐标是(2,2)或(10,-2);
(3)解:存在,理由如下,
设点A的坐标为,
B(0,0),C(4,0),
,,,
∠BAC=90°,
,即,
解得或,
所以,在直线l上存在点A,使∠BAC=90°,此时点A的坐标是(2,2)或(3.6,1.2).
(1) 当△ABC是以BC为底的等腰三角形时,点A在BC的中垂线上,由B、C两点的坐标可得BC的中垂线为x=2,即A点的横坐标为2,进而将x=2代入直线l的解析式算出对应的函数值,从而即可得出点A的坐标;
(2) 设A(a,b),根据三角形面积计算公式△ABC的面积= BC·|b| ,据此建立方程,求解可得b的值,然后将b的值代入直线l的解析式算出对应的自变量x的值,从而即可求出点A的坐标;
(3)根据直线l上的点的坐标特点设A ,根据两点间的距离公式分别表示出AB2、AC2、BC2然后根据勾股定理建立方程,如果方程有解就存在,方程没有解,就不存在.
24.(1)解:∵、、和是四个全等的直角三角形,,,,
∴AH=DE=b,
,
,
,
,
四个直角三角形的面积和
(2)解:由可知四个直角三角形的面积和为,
,解得,
,
(1)根据全等三角形性质得AH=DE=b,即可求得正正方形EFGH的边长,从而可得该正方形的面积,然后用大正方形面积-小正方形面积即可得四个直角三角形的面积和.
(2)根据,利用a2+b2=c2求a2+b2得的值.利用直角三角形的面积计算公式和面积和求得ab的值,代入即可得到的值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
保密★启用前
20224-2025学年八年级下册开学摸底考试(浙教版)
数学
考试范围:八上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本大题有10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在下列图形中, 是轴对称图形有 ( ) 个
A.1 B.2 C.3 D.4
2.某农户买黄金瓜,第一天上午买了45斤,价格为每斤x元,下午他又买了35斤,价格为每斤y元.第二天他以每斤元的价格卖完了80斤,结果同第一天比发现自己亏了.其原因是( )
A. B. C. D.
3.象棋在中国有着三千多年的历史,如图是一方的棋盘,如果“帅”的坐标是(1,1),“卒”的坐标是(3,2),那么“马”的坐标是( )
A. B. C. D.
4.一次函数中,随的增大而增大,且,则这个函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,,,点、在上,那么添加下列一个条件后,仍无法判断的是( )
A. B. C. D.
6.下列命题的逆命题是真命题的是( )
A.直角三角形的两个锐角互余 B.对顶角相等
C.全等三角形的面积相等 D.全等三角形的对应角相等
7.若点A到x轴的距离是5,到y轴的距离是4,且点A在第二象限,则A的坐标为( ).
A. B. C. D.
8.对于一次函数,下列结论错误的是( )
A.函数图象与轴的交点坐标是
B.函数值随自变量的增大而减小
C.函数图象不经过第三象限
D.函数图象向下平移4个单位长度得的图象
9.如图,AB=4,动点P满足S△PAB=4,则PA+PB的最小值为( )
A.5 B. C. D.
10.已知菱形ABCD,E、F是动点,边长为5,,,则下列结论①;②为等边三角形;③;④若,则,正确的有几个( )
A.1 B.2 C.3 D.4
二、填空题(本大题有6小题,每小题3分,共18分)
11.关于x的不等式的最小整数解是 .
12.已知y是关于x的一次函数,下表列出了部分对应值,则m的值是 .
x 0 1 2
y 1 m 5
13.如图,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,部分点及坐标如下表:
第1个点 第2个点 第3个点 第4个点 第5个点 …
坐标 …
根据规律,填空:
(1)第7个点的坐标为.
(2)第2025个点的坐标为.(注)
14. 已知线段AB=11 cm,在直线 AB上画线段BC,使BC=3cm,则线段 AC= cm。
15.如图,在平面直角坐标系中,已知点与点关于轴对称,现将点向右平移个单位得到点,若直线BC经过点,则的值为 .
16.如图,在中,,,点是边上的点,将沿折叠得到,点是点的对称点.若为,则的长是 .
三、解答题(本题有8小题,共72分.解答应写出必要的文字说明,证明过程或演算步骤)
17.(1)计算:
(2)下面是小明同学解不等式的过程,请认真阅读并完成相应任务.
解:……第一步
……第二步
……第三步
……第四步
……第五步
任务一:填空:①以上解题过程中,第二步是依据_________(运算律)进行变形的;
②第_________步开始出现错误,这一步错误的原因是_________;
任务二:请直接写出该不等式的正确解集.
18.如图所示,在△ABC中,AB=AC,∠1=∠2,AD⊥CD于点D,AE⊥BE于点E,BE,CD交于点O.
求证:(1)△ABE≌△ACD;
(2)OD=OE.
19.如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,2).
(1)填空:点A关于x轴对称的点的坐标是 ,点B关于y轴对称的点的坐标是 ;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到.请写出的三个顶点坐标;
(3)求△ABC的面积.
20.如图,在 ABC中AD、AE、AF分别为△ABC的高、角平分线和中线,已知 AFC的面积为10,AD=4,∠DAE=20°,∠C=30°.
(1)求BC的长度;
(2)求∠B的度数.
21.一次函数的图象经过,两点.
(1)求此函数的表达式.
(2)试判断点是否在此函数的图象上,并说明理由.
22.倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出A型和B型两款垃圾分拣机器人,已知2台A型机器人和5台B型机器人同时工作2小时共分拣垃圾3.6吨,3台A型机器人和2台B型机器人同时工作5小时共分拣垃圾8吨.
(1)1台A型机器人和1台B型机器人每小时各分拣垃圾多少吨?
(2)某垃圾处理厂计划向机器人公司购进一批A型和B型垃圾分拣机器人,机器人公司的报价如下表:
型号 原价 购买量少于30台 购买量不少于30台
A型 20万元/台 原价购买 打九折
B型 12万元/台 原价购买 打八折
①若要求这批机器人每小时一共能分拣垃圾20吨.设其中购买A型机器人x台(10≤x≤35),购买两种机器人总费用为W万元.求W与x的函数关系式,并说明如何购买总费用最少;
②为了加快垃圾分拣速度,垃圾处理厂计划用不超过140万元增购这两种机器人共10台,机器人公司全部以打折后价格销售,这10台机器人每小时最多处理多少吨垃圾?
23.如图,△ABC的两顶点分别为B(0,0),C(4,0),顶点A在直线l:y=-x+3上.
(1)当△ABC是以BC为底的等腰三角形时,求点A的坐标;
(2)当△ABC的面积为4时,求点A的坐标;
(3)在直线l上是否存在点A,使∠BAC=90°?若存在,求出点A的坐标;若不存在请说明理由.
24.如图是“赵爽弦图”,其中、、和是四个全等的直角三角形,四边形和都是正方形,根据这个图形的面积关系,可以证明勾股定理设,,,取,.
(1)求四个直角三角形的面积和;
(2)求的值.
答案解析部分
1.C
解:第一、第二、第四个图形都能找到这样的一条直线,使这些图形沿着一条直线对折后两部分完全重合,所以是轴对称图形,
第三个图形找到这样的一条直线,使这个图形沿着一条直线对折后两部分完全重合,所以不是轴对称图形,
所以是轴对称图形有3个.
故答案为:C.
利用轴对称图形的定义(如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴)逐项分析判断即可.
2.B
3.C
解:如图所示,建立平面直角坐标系,在“马"的坐标是(-1,2),
故答案为:C.
本题考查建立平面直角坐标系。根据题中所给点的坐标,确定原点和坐标轴即可。
4.B
解: 一次函数中,随的增大而增大,且,
则 k>0,b<0
则一次函数过第一、三、四象限,不过第二象限。
故答案为:B.
本题考查一次函数的性质和象限。当k>0,b>0时,一次函数y=kx+b(k≠0)过第一、二、三象限;当k>0,b<0时,一次函数y=kx+b(k≠0)过第一、三、四象限;当k<0,b>0时,一次函数y=kx+b(k≠0)过第一、二、四象限;当k<0,b<0时,一次函数y=kx+b(k≠0)过第二、三、四象限。熟练掌握一次函数的性质很关键。
5.D
6.A
解:A、逆命题是:两个锐角互余的三角形是直角三角三角形,是真命题,故此选项正确,符合题意;
B、逆命题是:相等的角是对顶角,是假命题,故此选项错误,不符合题意;
C、逆命题是:三个角对应相等的两个三角形全等,是假命题,故此选项错误,不符合题意;
D、逆命题是:面积相等的三角形是全等三角形,是假命题,故此选项错误,不符合题意.
故答案为:A.
先写出命题的逆命题,再判断真假即可求解.
7.B
8.A
解:A、一次函数y=-x+4中,令y=0,得-x+4=0,解得x=4,所以该一次函数图象与x轴的交点坐标为(4,0),故此选项错误,符合题意;
B、一次函数y=-x+4中,自变量的系数k=-1<0,所以数值随自变量的增大而减小,故此选项正确,不符合题意;
C、一次函数y=-x+4中,自变量的系数k=-1<0,所以函数图象经过第二、四象限;一次函数y=-x+4中,常数项b=4>0,所以图象交y轴的正半轴,所以该函数图象经过一、二、四象限,即函数图象不经过第三象限,故此选项正确,不符合题意;
D、一次函数y=-x+4中,向下平移4个单位长度后的函数解析式为y=-x+4-4=-x,故此选项正确,不符合题意.
故答案为:A.
令一次函数解析式中的y=0算出对应的自变量x的值,即可得出该函数图象与x轴交点的坐标,据此可判断A选项;
一次函数y=ax+b(a≠0),当a>0时,函数值随自变量的增大而增大,当a<0时,函数值随自变量的增大而减小,据此可判断B选项;
一次函数y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象限;当a>0,b<0时,图象过一、三、四象限;当a>0,b=0时,图象过一、三象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限,当a<0,b=0时,图象过二、四象限,据此可判断C选项;
一次函数y=ax+b(a≠0)图象的平移规律是“左移加,右移减;上移加,下移减”,据此可判断D选项.
9.D
解:由题意,△PAB的高为4×2÷4=2,则P点在与AB平行且距离AB为2的直线l上,
如图,作A关于直线l对称点A',连接A'B,A'P,
则PA'=PA,PA+PB=PA'+PB≥A'B,A'B即为所求最小值,
Rt△A'AB中,A'A=2×2=4,AB=4,则A'B=
故答案为:D.
先算出三角形的高,得到P点在与AB平行且距离AB为2的直线l上,作A关于直线l对称点A',则A'B即为所求最小值,利用勾股定理求解即可.
10.D
解:①四边形是菱形,∠BAD=120°,
∴AB=BC,AD∥BC,,
,
∴∠B=∠CAF=60°,
∴是等边三角形,
∴BC=AC,
在和中,
,
∴,故①正确;
②∵,
,,
∵是等边三角形,
∴∠ACB=∠BCE+∠ACE=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=∠ECF=60°,
∴是等边三角形,故②正确;
③∵是等边三角形,
∴∠CFG=60°,
,,
,故③正确;
④如图,过点作EM//BC交于点,
易证是等边三角形,则,
∵AF//EM,
∴,故④正确,
故答案为:D.
①根据菱形的性质、平行线的性质证出AB=BC,∠B=∠CAF=60°,从而利用“SAS”可得,即可判断该结论正确;②由,得,,根据等边三角形的性质得∠ACB=∠BCE+∠ACE=60°,进行等量代换得∠ACF+∠ACE=∠ECF=60°,从而证出是等边三角形,即可判断该结论正确正确;③由等边三角形的性质、外角的性质得,即可判断该结论正确;④过点作EM//BC交下点点,易证是等边三角形,则,由AF//EM,则,即可判断该结论正确.
11.
12.3
13.,
14.8或14
解:分两种情况讨论:
①如图,当点C在线段上,
,,
;
②如图,当点C在线段的延长线上,
,,
,
综上可知,线段的长为或,
故答案为:或.
分两种情况讨论:①点C在线段上;②点C在线段的延长线上,分别求解即可得到答案.
15.4
解:∵ 点与点关于轴对称,
∴B(-1,-2),
设直线BC解析式为y=kx+b,
把B(-1,-2)代入解析式得,解得k=1,b=-1,
∴直线BC:y=x-1,
将点向右平移个单位得到点 ,则C(-1+m,2),
把点C坐标代入y=x-1中,得-1+m-1=2,
解得m=4.
故答案为:4.
先求出B坐标,再利用待定系数法求出直线BC解析式,由坐标的平移求C(-1+m,2),然后把点C坐标代入直线BC解析式即可求出m值.
16.2或4
解:作于点,
∵,,
∴,
∴,
∴,
当点在直线的下方时,如图,
由折叠的性质得,
∵,
∴,
∴,
∴,,
∴,,
∴;
当点在直线的上方时,如图,
∵,
∴,
∴,,
∴,,
∴,
∴.
综上,的长是2或4.
故答案为:2或4.
先根据30°角的直角三角形的性质得到,然后分两种情况讨论,利用等腰三角形的性质以及含30度角的直角三角形的性质即可解题.
17.(1);(2)任务一:①乘法分配律;②五,不等式两边都除以,不等号的方向没有改变;任务二:
18.证明:(1)∵AD⊥DC,AE⊥BE,
∴∠ADC=∠AEB=90°,
∵∠1=∠2,∠EAB=∠1+∠DAE,∠DAC=∠2+∠DAE,
∴∠DAC=∠EAB,
在与中,
,
∴;
(2)连接AO,如图,
∵,
∴AE=AD,
在和中,
,
∴,
∴OD=OE.
(1)根据垂直的定义得∠ADC=∠AEB=90°,然后根据角的和差关系得∠DAC=∠EAB,接下来由”AAS“即可得证结论;
(2)根据全等三角形对应边相等的性质得AE=AD,然后得证,于是根据全等三角形对应边相等即可得证结论.
19.(1)(2,1),(-4,3);(2)(0,0),(2,4),(-1,3);(3)5.
20.(1)解:∵AF是△ABC的中线,
∴BC=2BF=2CF,BF=CF,
∴△ABF和△ACF的面积相等,
∵△AFC的面积为10,
∴∠ABF的面积为10,
∵AD=4,
∴ =10,
∴BF=5,
∴BC=2BF=10;
(2)解:∵AD是△ABC的高,
∴∠ADC=90°,
∵∠DAE=20°,
∴∠AED=180°﹣90°﹣20°=70°,
∵∠C=30°,
∴∠CAE=∠AED﹣∠C=40°,
∵AE是△ABC的角平分线,
∴∠BAC=2∠CAE=80°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣80°﹣30°=70°.
(1)求出△ABF和△ACF的面积相等,根据三角形的面积求出BF,继而求出BC即可;
(2)求出∠AED的度数,根据三角形的外角的性质求出∠CAE,根据角平分线的含义求出∠BAC,继而由三角形的内角和定理求出∠B即可。
21.(1)解:设一次函数的解析式为,
一次函数的图象经过,两点,
,
解得,
此函数的表达式为;
(2)解:点不在此函数的图象上,
理由:把代入中得,,
点不在此函数的图象上.
(1)设一次函数解析式为y=kx+b,然后将M和N的坐标分别代入,构建方程组求出k和b的值,即用待定系数法求解即可;
(2)利用(1)中的解析式,通过计算自变量为3对应的函数值可判断点P是否在此函数的图象上。
22.(1)1台A型机器人每小时分拣0.4吨,1台B型机器人每小时分拣0.2吨;(2)①,购买A型35台,B型30台总费用最少;②3吨垃圾.
23.(1)解:如图,当△ABC是以BC为底的等腰三角形时,点A在BC的中垂线上.
∵B(0,0),C(4,0),
∴BC的中垂线为x=2.
又点A在直线l:y=-x+3上,
∴y=-×2+3=2,
即A(2,2);
(2)解:设A(a,b).则依题意得
BC·|b|=4,即×4|b|=4,
解得|b|=2
∴b=±2.
①当b=2时,2=-a+3,
解得 a=2
则A(2,2);
②当b=-2时,-2=-a+3,
解得 a=10
则A(10,-2).
综上所述,点A的坐标是(2,2)或(10,-2);
(3)解:存在,理由如下,
设点A的坐标为,
B(0,0),C(4,0),
,,,
∠BAC=90°,
,即,
解得或,
所以,在直线l上存在点A,使∠BAC=90°,此时点A的坐标是(2,2)或(3.6,1.2).
(1) 当△ABC是以BC为底的等腰三角形时,点A在BC的中垂线上,由B、C两点的坐标可得BC的中垂线为x=2,即A点的横坐标为2,进而将x=2代入直线l的解析式算出对应的函数值,从而即可得出点A的坐标;
(2) 设A(a,b),根据三角形面积计算公式△ABC的面积= BC·|b| ,据此建立方程,求解可得b的值,然后将b的值代入直线l的解析式算出对应的自变量x的值,从而即可求出点A的坐标;
(3)根据直线l上的点的坐标特点设A ,根据两点间的距离公式分别表示出AB2、AC2、BC2然后根据勾股定理建立方程,如果方程有解就存在,方程没有解,就不存在.
24.(1)解:∵、、和是四个全等的直角三角形,,,,
∴AH=DE=b,
,
,
,
,
四个直角三角形的面积和
(2)解:由可知四个直角三角形的面积和为,
,解得,
,
(1)根据全等三角形性质得AH=DE=b,即可求得正正方形EFGH的边长,从而可得该正方形的面积,然后用大正方形面积-小正方形面积即可得四个直角三角形的面积和.
(2)根据,利用a2+b2=c2求a2+b2得的值.利用直角三角形的面积计算公式和面积和求得ab的值,代入即可得到的值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
