2024-2025学年七年级下学期数学(北师大版)开学摸底考试(含答案)
文档属性
| 名称 | 2024-2025学年七年级下学期数学(北师大版)开学摸底考试(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
保密★启用前
20224-2025学年七年级下册开学摸底考试(北师大版)
数学
考试范围:七上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(共10题;共35分)
1. -5的倒数的相反数是 ( )
A. B .C.5 D. -5
2.单项式的系数是( )
A. B.2 C.3 D.5
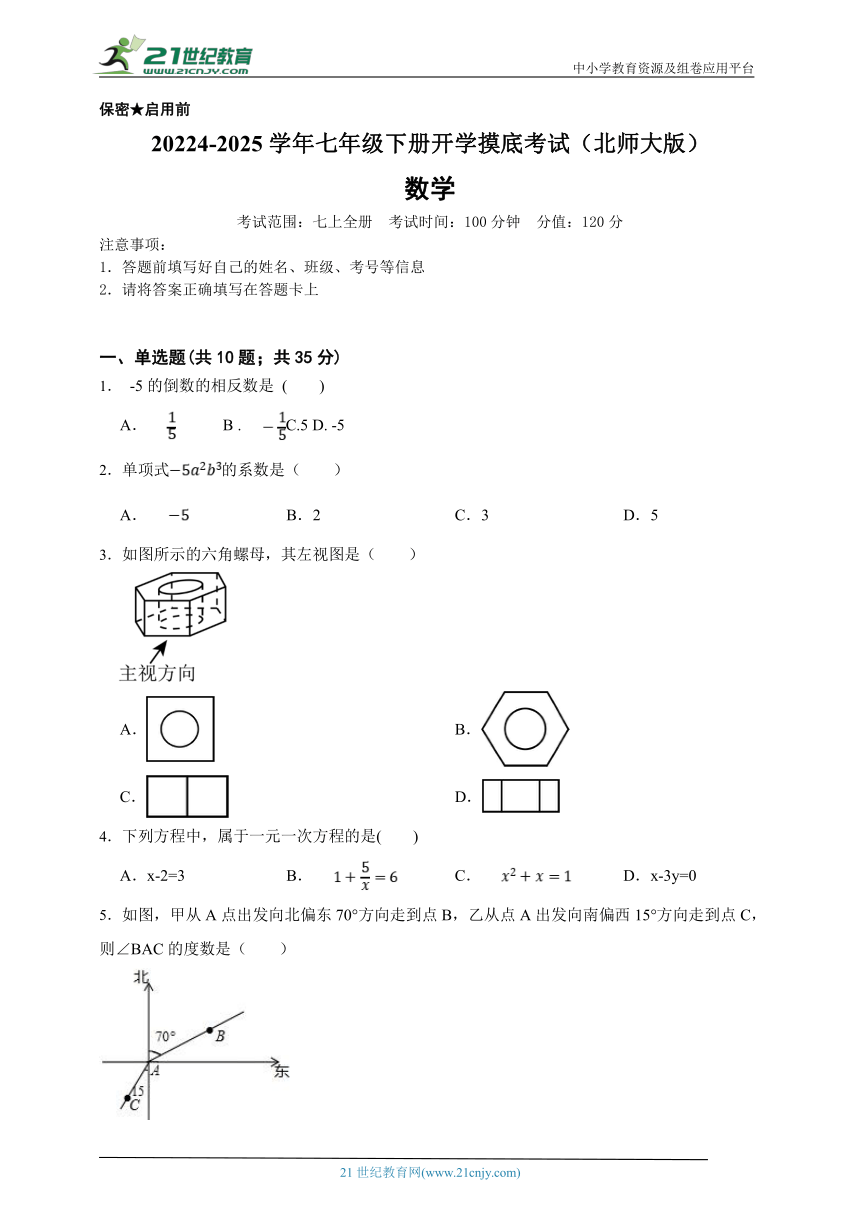
3.如图所示的六角螺母,其左视图是( )
A. B.
C. D.
4.下列方程中,属于一元一次方程的是( )
A.x-2=3 B. C. D.x-3y=0
5.如图,甲从A点出发向北偏东70°方向走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是( )
A.85° B.105° C.125° D.160°
6.下列调查方式合适的是( )
A.为了解市民对电影《血战狙击岭》的感受,黎明在学校随机采访了10名初一学生
B.为了解全班学生每天完成课外作业的时间,小莹同学在网上向3位好友做了调查
C.为了解全国青少年儿童的每天睡眠时间,统计人员采用了普查的方式
D.为了解“神舟十五号”载人飞船发射前零部件的状况,检测人员采用了普查的方式
7.下列计算正确的是( )
A.2(a+2)=2a+2 B.a+a=a2
C.3a 5a=15a2 D.(a+b)2=a2+b2
8.下面是乐乐在整理七年级上册课本知识点时得出的一些结论,你认为正确的有( )
①射线与射线是同一条射线;
②连接两点间的线段叫做这两点间的距离;
③要将一根木条固定在墙上至少需要两颗钉子的原理是两点确定一条直线;
④将弯曲的河道改直,可以缩短航程,其依据是两点之间线段最短.
A.0个 B.1个 C.2个 D.3个
9.如图,C 是线段AB 上一点,M 是AC 的中点,N 是 BC 的中点。若 MC 比 NC 长2cm,则AC比BC长 ( )
A.2cm B.4 cm C.1 cm D.6 cm
10.如图,将一条两边互相平行的纸带折叠.若∠1∶∠2=4∶3,则∠3的度数为( )
A.100° B.105° C.108° D.144°
二、填空题(共10题;共10分)
11.有理数80900000用科学记数法可表示为 .
12.已知.则的余角是 .
13.如图,直线与直线分别交于点,,与的角平分线交于点,与交于点,点是上一点,且,连接,是上一点使,作平分,交于点,,则 .
14.若实数、满足等式:,则 .
15.如图,一艘渔船向东航行,8点到达O处,灯塔A在其北偏东60°方向,距离16海里,10点到达B处,灯塔A在其正北方向,此时渔船与灯塔A相距 海里.
16.已知,,,求 .
17.如图,已知AB∥CD,CE,BE的交点为点E,现进行如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为点E1;
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为点E2;
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为点E3;
……
第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为点En.
若,则∠BEC等于 °.
18.如果有理数a、b、c在数轴上的位置如图所示,则 .
19.在一个装有水的圆柱形容器内,竖直插有一根圆柱形玻璃棒(实心),此时容器内水的高度为 80 cm,玻璃棒浸没在水中的长度大于 40 cm.已知容器内侧底面直径为20cm,玻璃棒的底面直径为5cm .现在把这根玻璃棒轻轻向正上方提起30cm,则水面下降了 cm.
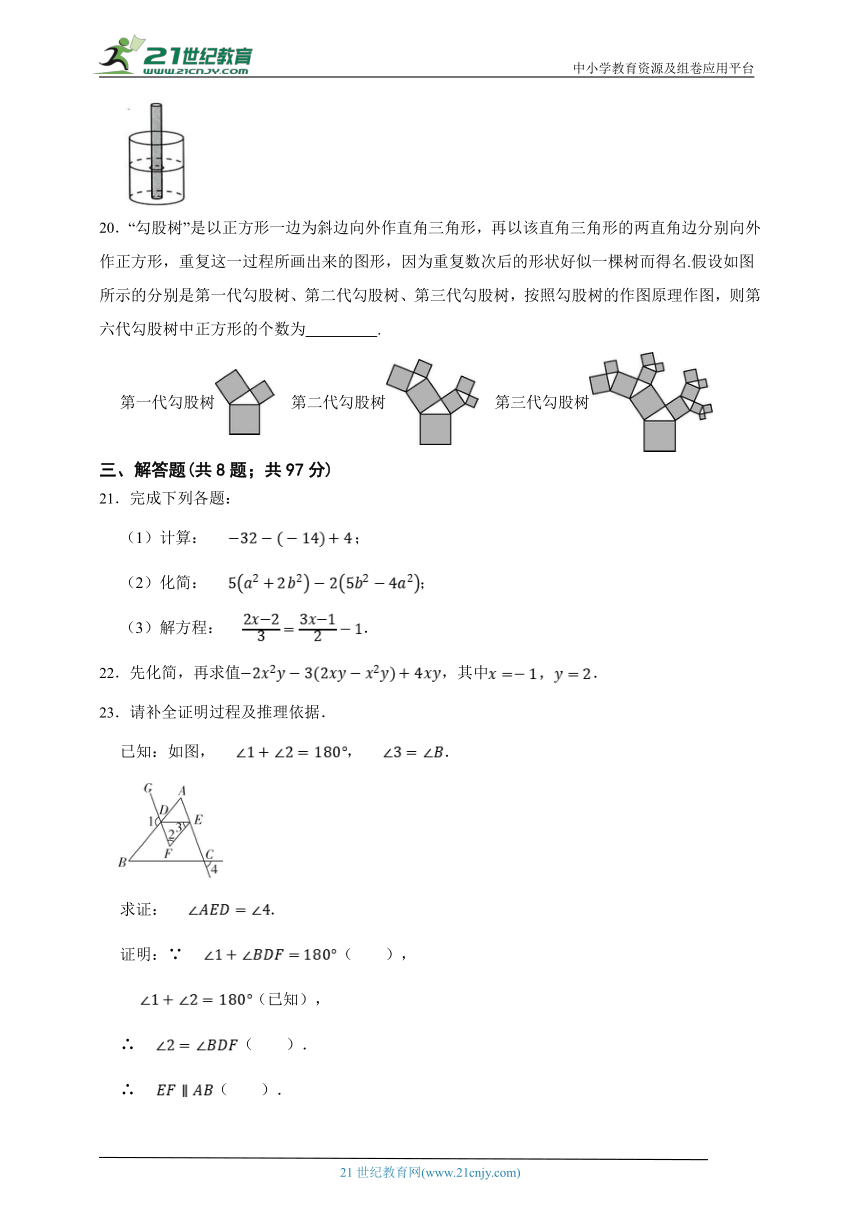
20.“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图所示的分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为 .
第一代勾股树 第二代勾股树 第三代勾股树
三、解答题(共8题;共97分)
21.完成下列各题:
(1)计算:;
(2)化简:;
(3)解方程:.
22.先化简,再求值,其中.
23.请补全证明过程及推理依据.
已知:如图,,.
求证:.
证明:∵( ),
(已知),
∴( ).
∴( ).
∴( ).
∵(已知),
∴ ▲ .
∴( ).
∴( ).
又∵( ),
∴.
24.打造书香文化,培养阅读习惯,崇德中学计划在各班建图书角,开展“我最喜欢阅读的书篇”为主题的调查活动,学生根据自己的爱好选择一类书籍(A:科技类,B:文学类,C:政史类,D:艺术类,E:其他类).张老师组织数学兴趣小组对学校部分学生进行了问卷调查,根据收集到的数据,绘制了两幅不完整的统计图(如图所示).
根据图中信息,请回答下列问题;
(1)条形图中的 , ,文学类书籍对应扇形圆心角等于 度;
(2)若该校有2000名学生,请你估计最喜欢阅读政史类书籍的学生人数;
(3)甲同学从A,B,C三类书籍中随机选择一种,乙同学从B,C,D三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.
25.已知∠AOB=100°,射线 OC 在∠AOB 的内部,射线OE,OF 分别是∠AOC 和∠COB 的平分线。
(1)如图①,若∠AOC=30°,求∠EOF 的度数。
(2)①如图②,若射线OC 在∠AOB 的内部绕点O 旋转,求∠EOF 的度数。
②若射线OC 在∠AOB 的外部绕点O 旋转(旋转中∠AOC,∠BOC 均指小于180°的角),其余条件不变,请借助图③探究∠EOF 的度数。
26.工大附中某楼窗户的形状如图所示(图中长度单位:米),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是米.(取3)
(1)求窗户的面积;
(2)求窗户的外框(半圆和大正方形)的总长;
(3)当时,为了隔音保暖,窗户安装的是带有分隔线的双层玻璃,每层这样的玻璃每平方米20元,窗户外框材料每米30元,求制作这样一个窗户需要多少钱?
27.今年义乌市准备争创全国卫生城市,某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
28.如图,直线与的两边交于,两点,,点是边上一个动点,连接.
(1)过点作,交射线于点,依题意补全图形,
①直接写出的度数(用含α的式子表示);
②若点,在,的延长线上,并且直线,当平分时,求的度数(用含的式子表示);小林在思考这道题时,想到过点作交射线于点,通过转化角可以求出的度数.你可以利用小林的思路解答此题也可以独立思考求出的度数.
(2)参考小林思考问题的方法,解决问题:若点,在,的延长线上,并且直线,当点在上运动时,直接用含的等式表示,,的数量关系.
答案解析部分
1.A
2.A
3.C
4.A
5.C
6.D
7.C
8.C
9.B
10.C
11.8.09×107
12.34°30′
13.
14.
15.8
16.
17.
18.-1-c
19.2
20.127
21.(1)
(2)
(3)
22.解:原式,
当时,原式.
23.解:证明:∵(邻补角的定义),
(已知),
∴(同角的补角相等).
∴(内错角相等,两直线平行)
∴(两直线平行,内错角相等).
∵(已知),
∴.
∴(同位角相等,两直线平行).
∴(两直线平行,同位角相等).
又∵(对顶角相等),
∴.
24.(1)18;6;
(2)解:(人),
因此估计最喜欢阅读政史类书籍的学生人数为480人;
(3)解:画树状图如下:
由图可知,共有9种等可能的情况,其中甲乙两位同学选择相同类别书籍的情况有2种,
因此甲乙两位同学选择相同类别书籍的概率为:.
25.(1)解: ∵∠AOB=100°,∠AOC=30°,
∴∠BOC=∠AOB-∠AOC=70°。
∵OE,OF 分别是∠AOC 和∠COB 的平分线,
(2)解: ①∵OE,OF 分别是∠AOC 和∠COB 的平分线,
②分两种情况讨论:
i.射线OE,OF 只有一条在∠AOB 的外部,如解图①,此时
ii.射线OE,OF 都在∠AOB 的外部,如解图②,此时
综上所述,∠EOF 的度数为50°或130
26.(1)平方米
(2)米
(3)元
27.(1)解:设温情提示牌的单价为x元,则垃圾箱的单价为3x元,
根据题意得,2x+3×3x=550,
∴x=50,
经检验,符合题意,
∴3x=150元,
即:温馨提示牌和垃圾箱的单价各是50元和150元;
(2)解:设购买温情提示牌y个(y为正整数),则垃圾箱为(100﹣y)个,
根据题意得,意,
∴
∵y为正整数,
∴y为50,51,52,共3中方案;
有三种方案:①温馨提示牌50个,垃圾箱50个,
②温馨提示牌51个,垃圾箱49个,
③温馨提示牌52个,垃圾箱48个,
设总费用为w元
W=50y+150(100﹣y)=﹣100y+15000,
∵k=-100 ,∴w随y的增大而减小
∴当y=52时,所需资金最少,最少是9800元.
28.(1)解:①补图如下,
∵,
∴,
∵,
∴;
②如下图,
∵,,
∴,
∵平分,
∴,
∵,
∴,
∵,
∴;
(2)或或.
过点作交射线于点,
当点在线段上时,如下图,
∵,,
∴,,
∵,
∴,
当点在线段上时,如下图,
∵,,
∴,,
∵,
∴,
∵,
∴,
∴;
当点在射线上时,如下图,
∵,,
∴,,
∴,
∵,,
∴,
∴.
综上所述,或或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
保密★启用前
20224-2025学年七年级下册开学摸底考试(北师大版)
数学
考试范围:七上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(共10题;共35分)
1. -5的倒数的相反数是 ( )
A. B .C.5 D. -5
2.单项式的系数是( )
A. B.2 C.3 D.5
3.如图所示的六角螺母,其左视图是( )
A. B.
C. D.
4.下列方程中,属于一元一次方程的是( )
A.x-2=3 B. C. D.x-3y=0
5.如图,甲从A点出发向北偏东70°方向走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是( )
A.85° B.105° C.125° D.160°
6.下列调查方式合适的是( )
A.为了解市民对电影《血战狙击岭》的感受,黎明在学校随机采访了10名初一学生
B.为了解全班学生每天完成课外作业的时间,小莹同学在网上向3位好友做了调查
C.为了解全国青少年儿童的每天睡眠时间,统计人员采用了普查的方式
D.为了解“神舟十五号”载人飞船发射前零部件的状况,检测人员采用了普查的方式
7.下列计算正确的是( )
A.2(a+2)=2a+2 B.a+a=a2
C.3a 5a=15a2 D.(a+b)2=a2+b2
8.下面是乐乐在整理七年级上册课本知识点时得出的一些结论,你认为正确的有( )
①射线与射线是同一条射线;
②连接两点间的线段叫做这两点间的距离;
③要将一根木条固定在墙上至少需要两颗钉子的原理是两点确定一条直线;
④将弯曲的河道改直,可以缩短航程,其依据是两点之间线段最短.
A.0个 B.1个 C.2个 D.3个
9.如图,C 是线段AB 上一点,M 是AC 的中点,N 是 BC 的中点。若 MC 比 NC 长2cm,则AC比BC长 ( )
A.2cm B.4 cm C.1 cm D.6 cm
10.如图,将一条两边互相平行的纸带折叠.若∠1∶∠2=4∶3,则∠3的度数为( )
A.100° B.105° C.108° D.144°
二、填空题(共10题;共10分)
11.有理数80900000用科学记数法可表示为 .
12.已知.则的余角是 .
13.如图,直线与直线分别交于点,,与的角平分线交于点,与交于点,点是上一点,且,连接,是上一点使,作平分,交于点,,则 .
14.若实数、满足等式:,则 .
15.如图,一艘渔船向东航行,8点到达O处,灯塔A在其北偏东60°方向,距离16海里,10点到达B处,灯塔A在其正北方向,此时渔船与灯塔A相距 海里.
16.已知,,,求 .
17.如图,已知AB∥CD,CE,BE的交点为点E,现进行如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为点E1;
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为点E2;
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为点E3;
……
第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为点En.
若,则∠BEC等于 °.
18.如果有理数a、b、c在数轴上的位置如图所示,则 .
19.在一个装有水的圆柱形容器内,竖直插有一根圆柱形玻璃棒(实心),此时容器内水的高度为 80 cm,玻璃棒浸没在水中的长度大于 40 cm.已知容器内侧底面直径为20cm,玻璃棒的底面直径为5cm .现在把这根玻璃棒轻轻向正上方提起30cm,则水面下降了 cm.
20.“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图所示的分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为 .
第一代勾股树 第二代勾股树 第三代勾股树
三、解答题(共8题;共97分)
21.完成下列各题:
(1)计算:;
(2)化简:;
(3)解方程:.
22.先化简,再求值,其中.
23.请补全证明过程及推理依据.
已知:如图,,.
求证:.
证明:∵( ),
(已知),
∴( ).
∴( ).
∴( ).
∵(已知),
∴ ▲ .
∴( ).
∴( ).
又∵( ),
∴.
24.打造书香文化,培养阅读习惯,崇德中学计划在各班建图书角,开展“我最喜欢阅读的书篇”为主题的调查活动,学生根据自己的爱好选择一类书籍(A:科技类,B:文学类,C:政史类,D:艺术类,E:其他类).张老师组织数学兴趣小组对学校部分学生进行了问卷调查,根据收集到的数据,绘制了两幅不完整的统计图(如图所示).
根据图中信息,请回答下列问题;
(1)条形图中的 , ,文学类书籍对应扇形圆心角等于 度;
(2)若该校有2000名学生,请你估计最喜欢阅读政史类书籍的学生人数;
(3)甲同学从A,B,C三类书籍中随机选择一种,乙同学从B,C,D三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.
25.已知∠AOB=100°,射线 OC 在∠AOB 的内部,射线OE,OF 分别是∠AOC 和∠COB 的平分线。
(1)如图①,若∠AOC=30°,求∠EOF 的度数。
(2)①如图②,若射线OC 在∠AOB 的内部绕点O 旋转,求∠EOF 的度数。
②若射线OC 在∠AOB 的外部绕点O 旋转(旋转中∠AOC,∠BOC 均指小于180°的角),其余条件不变,请借助图③探究∠EOF 的度数。
26.工大附中某楼窗户的形状如图所示(图中长度单位:米),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是米.(取3)
(1)求窗户的面积;
(2)求窗户的外框(半圆和大正方形)的总长;
(3)当时,为了隔音保暖,窗户安装的是带有分隔线的双层玻璃,每层这样的玻璃每平方米20元,窗户外框材料每米30元,求制作这样一个窗户需要多少钱?
27.今年义乌市准备争创全国卫生城市,某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
28.如图,直线与的两边交于,两点,,点是边上一个动点,连接.
(1)过点作,交射线于点,依题意补全图形,
①直接写出的度数(用含α的式子表示);
②若点,在,的延长线上,并且直线,当平分时,求的度数(用含的式子表示);小林在思考这道题时,想到过点作交射线于点,通过转化角可以求出的度数.你可以利用小林的思路解答此题也可以独立思考求出的度数.
(2)参考小林思考问题的方法,解决问题:若点,在,的延长线上,并且直线,当点在上运动时,直接用含的等式表示,,的数量关系.
答案解析部分
1.A
2.A
3.C
4.A
5.C
6.D
7.C
8.C
9.B
10.C
11.8.09×107
12.34°30′
13.
14.
15.8
16.
17.
18.-1-c
19.2
20.127
21.(1)
(2)
(3)
22.解:原式,
当时,原式.
23.解:证明:∵(邻补角的定义),
(已知),
∴(同角的补角相等).
∴(内错角相等,两直线平行)
∴(两直线平行,内错角相等).
∵(已知),
∴.
∴(同位角相等,两直线平行).
∴(两直线平行,同位角相等).
又∵(对顶角相等),
∴.
24.(1)18;6;
(2)解:(人),
因此估计最喜欢阅读政史类书籍的学生人数为480人;
(3)解:画树状图如下:
由图可知,共有9种等可能的情况,其中甲乙两位同学选择相同类别书籍的情况有2种,
因此甲乙两位同学选择相同类别书籍的概率为:.
25.(1)解: ∵∠AOB=100°,∠AOC=30°,
∴∠BOC=∠AOB-∠AOC=70°。
∵OE,OF 分别是∠AOC 和∠COB 的平分线,
(2)解: ①∵OE,OF 分别是∠AOC 和∠COB 的平分线,
②分两种情况讨论:
i.射线OE,OF 只有一条在∠AOB 的外部,如解图①,此时
ii.射线OE,OF 都在∠AOB 的外部,如解图②,此时
综上所述,∠EOF 的度数为50°或130
26.(1)平方米
(2)米
(3)元
27.(1)解:设温情提示牌的单价为x元,则垃圾箱的单价为3x元,
根据题意得,2x+3×3x=550,
∴x=50,
经检验,符合题意,
∴3x=150元,
即:温馨提示牌和垃圾箱的单价各是50元和150元;
(2)解:设购买温情提示牌y个(y为正整数),则垃圾箱为(100﹣y)个,
根据题意得,意,
∴
∵y为正整数,
∴y为50,51,52,共3中方案;
有三种方案:①温馨提示牌50个,垃圾箱50个,
②温馨提示牌51个,垃圾箱49个,
③温馨提示牌52个,垃圾箱48个,
设总费用为w元
W=50y+150(100﹣y)=﹣100y+15000,
∵k=-100 ,∴w随y的增大而减小
∴当y=52时,所需资金最少,最少是9800元.
28.(1)解:①补图如下,
∵,
∴,
∵,
∴;
②如下图,
∵,,
∴,
∵平分,
∴,
∵,
∴,
∵,
∴;
(2)或或.
过点作交射线于点,
当点在线段上时,如下图,
∵,,
∴,,
∵,
∴,
当点在线段上时,如下图,
∵,,
∴,,
∵,
∴,
∵,
∴,
∴;
当点在射线上时,如下图,
∵,,
∴,,
∴,
∵,,
∴,
∴.
综上所述,或或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
