07.第十二章 简单机械 评估测试卷(含答案)
文档属性
| 名称 | 07.第十二章 简单机械 评估测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 275.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-15 21:43:00 | ||
图片预览



文档简介
第十二章评估测试卷
(满分:100分 时间:60分钟)
一、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项最符合题意)
1.在如图所示的简单机械中,属于费力杠杆的是 ( )
A.羊角锤 B.镊子 C.铡刀 D.开瓶器
2.下列关于功、功率、机械效率的说法正确的是 ( )
A.做功多的机器机械效率一定高
B.功率小的机器做功慢
C.机械效率高的机械功率一定大
D.功率大的机器做功时间一定短
3.(2024重庆A卷中考)同学们模仿中药房的戥秤制作杆秤,用筷子做秤杆,用钩码做秤砣,用细线将秤盘系在A点。当不挂秤砣、且秤盘不放物体时,在O点提起提纽,秤杆水平平衡;当秤盘放
100 g物体、秤砣移到B点时,秤杆再次水平平衡,如图所示。在O点与B点两条刻线之间均匀地画上49条刻度线。下列说法正确的是 ( )
A.自制杆秤的每一格约表示2.08 g
B.称中药时B端翘起应减少中药恢复水平平衡
C.若秤砣磨损,则测量结果会比真实质量偏小
D.若将提纽移到O点右侧可以增大杆秤的量程
4.如图所示,O点为杠杆的支点,杠杆右端挂有重为G的物体,杠杆在力F1的作用下在水平位置平衡。如果用力F2代替力F1使杠杆仍在水平位置保持平衡,下列关系中正确的是( )
A.F1F2
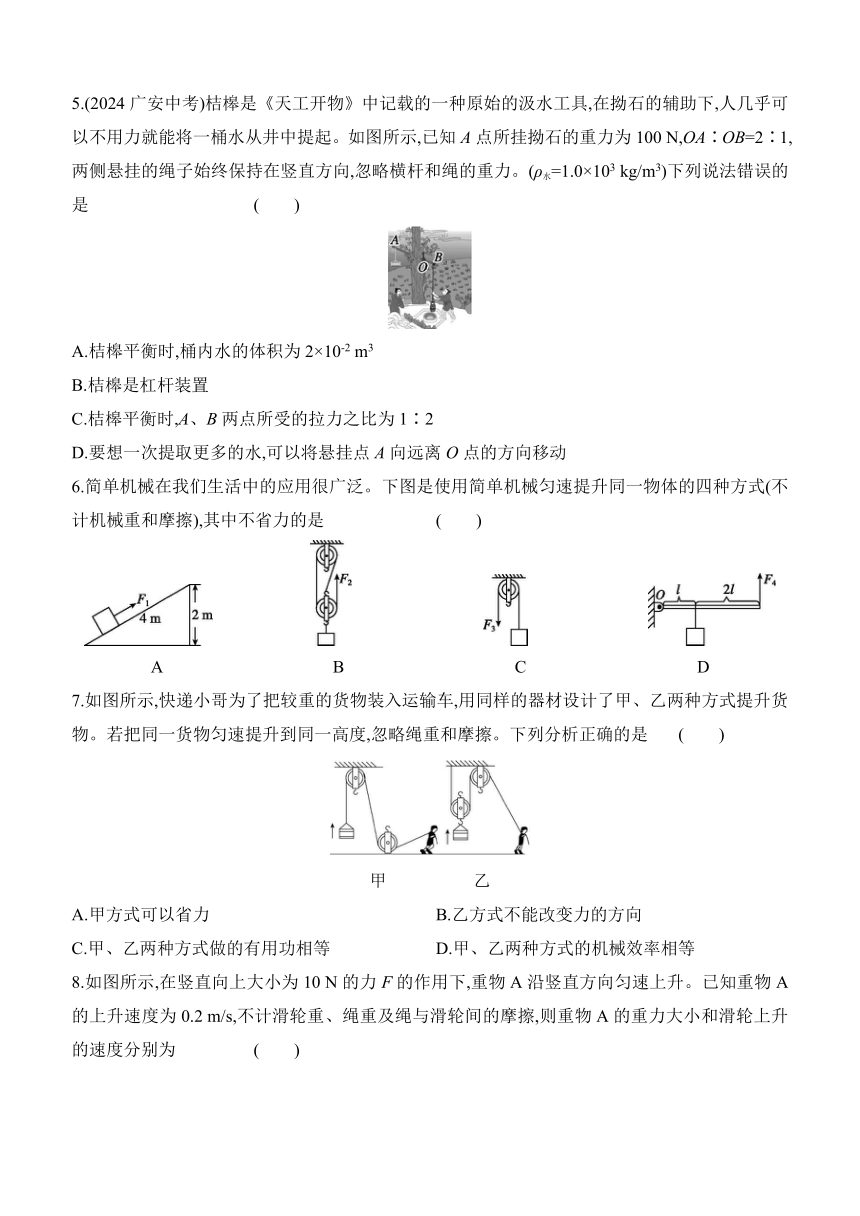
C.F25.(2024广安中考)桔槔是《天工开物》中记载的一种原始的汲水工具,在拗石的辅助下,人几乎可以不用力就能将一桶水从井中提起。如图所示,已知A点所挂拗石的重力为100 N,OA∶OB=2∶1,两侧悬挂的绳子始终保持在竖直方向,忽略横杆和绳的重力。(ρ水=1.0×103 kg/m3)下列说法错误的是 ( )
A.桔槔平衡时,桶内水的体积为2×10-2 m3
B.桔槔是杠杆装置
C.桔槔平衡时,A、B两点所受的拉力之比为1∶2
D.要想一次提取更多的水,可以将悬挂点A向远离O点的方向移动
6.简单机械在我们生活中的应用很广泛。下图是使用简单机械匀速提升同一物体的四种方式(不计机械重和摩擦),其中不省力的是 ( )
A B C D
7.如图所示,快递小哥为了把较重的货物装入运输车,用同样的器材设计了甲、乙两种方式提升货物。若把同一货物匀速提升到同一高度,忽略绳重和摩擦。下列分析正确的是 ( )
甲 乙
A.甲方式可以省力 B.乙方式不能改变力的方向
C.甲、乙两种方式做的有用功相等 D.甲、乙两种方式的机械效率相等
8.如图所示,在竖直向上大小为10 N的力F的作用下,重物A沿竖直方向匀速上升。已知重物A的上升速度为0.2 m/s,不计滑轮重、绳重及绳与滑轮间的摩擦,则重物A的重力大小和滑轮上升的速度分别为 ( )
A.20 N,0.4 m/s B.20 N,0.1 m/s C.5 N,0.4 m/s D.5 N,0.1 m/s
9.如图所示,甲、乙分别为同一滑轮组的不同绕法,忽略绳重及一切阻力,用图甲绕法匀速提升重为900 N的物体时,机械效率为90%。下列判断正确的是 ( )
甲 乙
A.拉力F1的大小为450 N
B.用图乙绕法匀速提升400 N的物体时,机械效率为80%
C.分别用两种绕法匀速提升相同的物体时,图乙绕法的机械效率大
D.分别用两种绕法匀速提升相同物体升高相同高度,F2做功少
10.如图所示,利用轻质滑轮组匀速拉动水平地面上重为G的物体。若拉力的大小为F,物体和地面之间的摩擦力大小为f,A点的拉力为FA,则下列滑轮组的机械效率表达式正确的是 ( )
A. B. C. D.
二、填空及作图题(本大题共5小题,每空2分,每图2分,共24分)
11.学习了杠杆知识后,小明将一个胡萝卜分成了两部分,如图所示,根据杠杆平衡的条件可得出A端胡萝卜相比B端胡萝卜 (选填“更重些”“一样重”或“更轻些”)。
12.在均匀直尺的中央挖一小凹槽,把一个薄金属片的一端插入橡皮中,另一端支在直尺的凹槽内制成一个简易“天平”。静止时直尺水平平衡。在直尺的两侧各放一个相同的小盘,在小盘中倒入质量不等的大米和小米,调整小盘在直尺上的位置,使直尺再次水平平衡,如图所示。由图可知,大米的质量 (选填“大于”或“小于”)小米的质量。F是左盘对直尺施加的力,请在图中画出F的力臂。现向左盘中再加入少量大米,写出一种能够使直尺恢复平衡的方法: 。
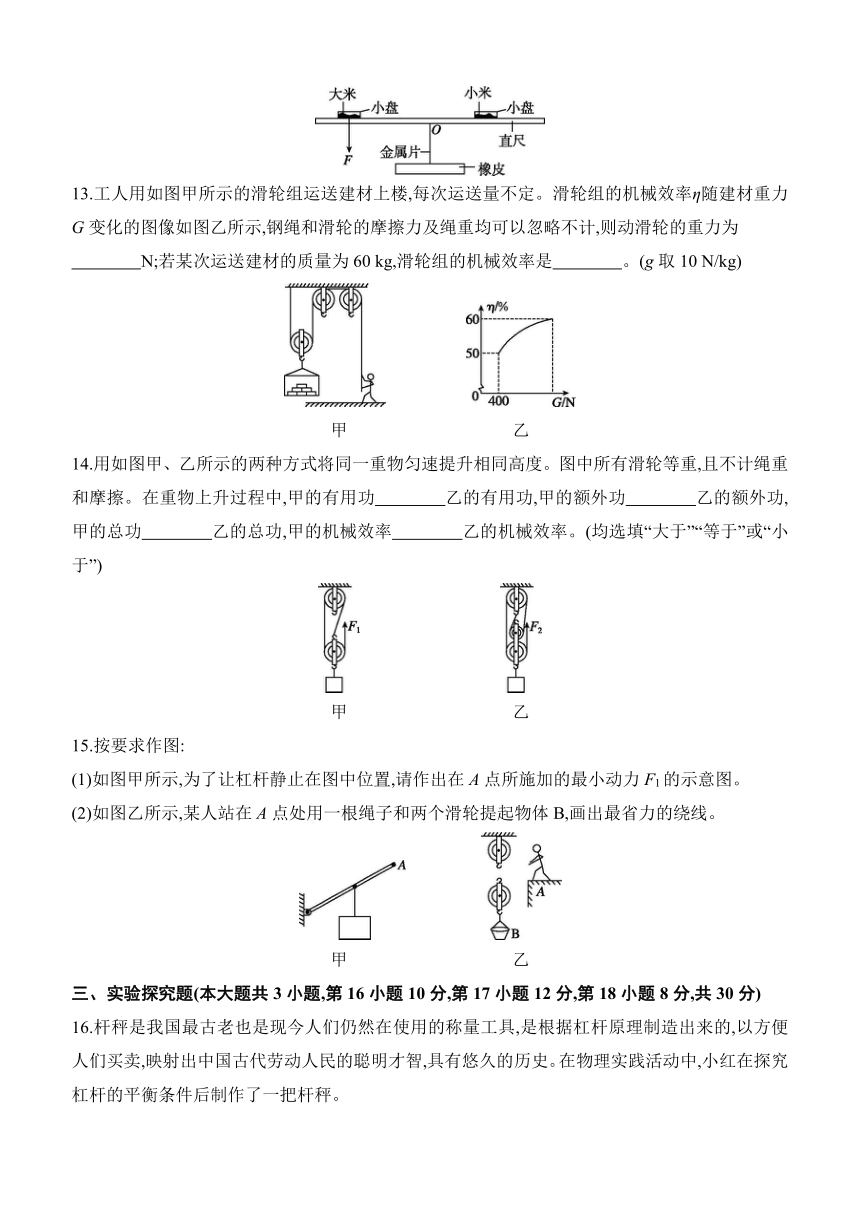
13.工人用如图甲所示的滑轮组运送建材上楼,每次运送量不定。滑轮组的机械效率η随建材重力G变化的图像如图乙所示,钢绳和滑轮的摩擦力及绳重均可以忽略不计,则动滑轮的重力为
N;若某次运送建材的质量为60 kg,滑轮组的机械效率是 。(g取10 N/kg)
甲 乙
14.用如图甲、乙所示的两种方式将同一重物匀速提升相同高度。图中所有滑轮等重,且不计绳重和摩擦。在重物上升过程中,甲的有用功 乙的有用功,甲的额外功 乙的额外功,甲的总功 乙的总功,甲的机械效率 乙的机械效率。(均选填“大于”“等于”或“小于”)
甲 乙
15.按要求作图:
(1)如图甲所示,为了让杠杆静止在图中位置,请作出在A点所施加的最小动力F1的示意图。
(2)如图乙所示,某人站在A点处用一根绳子和两个滑轮提起物体B,画出最省力的绕线。
甲 乙
三、实验探究题(本大题共3小题,第16小题10分,第17小题12分,第18小题8分,共30分)
16.杆秤是我国最古老也是现今人们仍然在使用的称量工具,是根据杠杆原理制造出来的,以方便人们买卖,映射出中国古代劳动人民的聪明才智,具有悠久的历史。在物理实践活动中,小红在探究杠杆的平衡条件后制作了一把杆秤。
甲 乙 丙
(1)实验前,杠杆静止时如图甲所示,此时应将杠杆的平衡螺母向 调,直至杠杆在水平位置平衡。
(2)杠杆水平平衡后,在杠杆左边A点处挂3个相同的钩码,如图乙所示,要使杠杆平衡,应在杠杆右边B点处挂 个同样的钩码。
(3)小红想用弹簧测力计进行实验,将B点所挂钩码取下,用弹簧测力计倒挂在B点并竖直向下拉,使杠杆水平平衡,此时弹簧测力计的示数将 (选填“大于”“小于”或“等于”)B点原本所挂钩码重力的大小。
(4)实验结束后,小红制作了如图丙所示的杆秤,该杆秤有2个提纽。若提起提纽1,秤盘不放物体,将秤砣移至某一点使杆秤恰好水平平衡,那么该点标定的刻度应为 ;以此类推,在秤盘上放1 g的物体,移动秤砣,使杆秤在水平位置处于平衡状态,在秤砣所挂的位置标定的刻度为1;然后在秤盘上放2 g的物体按上述方法直至标出所有刻度。
(5)若要增加称量的范围,应选用提纽 。
17.提高机械效率可以充分发挥机械设备的作用,对节能减排、提高经济效益有重要的意义。某科技创新小组根据生活经验和客观事实,对影响滑轮组机械效率的因素作出如下猜想:
猜想I:滑轮组的机械效率与物体被提升的高度有关;
猜想Ⅱ:滑轮组的机械效率与动滑轮的重力有关;
猜想Ⅲ:滑轮组的机械效率与所提物体的重力有关。
根据猜想,运用图甲、乙、丙所示的装置进行了实验探究,测得的实验数据如下表所示。
甲 乙 丙
实验 次数 钩码的 重力G/N 钩码上升 高度h/m 绳端拉力 F/N 绳端移动 的距离s/m 机械 效率η
1 2 0.1 0.90 0.3 74.1%
2 4 0.1 1.50 0.3 88.9%
3 4 0.1 1.25 0.4
4 4 0.2 1.50 0.6 88.9%
(1)实验时应沿竖直方向 缓慢向上拉动弹簧测力计。
(2)分析表中数据可知:第3次实验是利用图 装置完成的,它的机械效率η= 。
(3)比较2、4两次实验数据,可验证猜想I是 (选填“正确”或“错误”)的。
(4)通过比较 (填实验序号)两次实验数据可得出结论:同一滑轮组提升重物时,物重越大,滑轮组的机械效率越高。
(5)通过比较2、3两次实验数据可得出结论:不同滑轮组提升相同重物时,动滑轮越重,滑轮组的机械效率 。
18.为了探究斜面的机械效率与斜面倾斜程度之间的关系,探究小组的同学利用木板、刻度尺、弹簧测力计、木块等器材设计了如图所示的实验装置,实验测得的数据如下表:
实验 次数 斜面倾 斜程度 木块重 力G/N 斜面高 度h/m 沿斜面拉 力F/N 斜面长 度s/m 机械 效率
1 较缓 3 0.2 1.6 1 37.5%
2 较陡 3 0.3 1.8 1
3 最陡 3 0.4 2.0 1 60%
请你根据表中的数据回答下列问题:
(1)第2次实验中,斜面的机械效率为 ,斜面对木块的摩擦力为 N。
(2)斜面的机械效率与斜面的倾斜程度之间的关系是 。
(3)试列举出生活中利用斜面的一个实例: 。
四、计算应用题(本大题共2小题,第19小题8分,第20小题8分,共16分。解答时,要求有必要的文字说明、公式和计算步骤等,只写最后结果不得分)
19.如图是一辆汽车通过滑轮组将深井中的物体拉至井口的装置图,已知井深10 m,物体重G=4×103 N,汽车重G车=3×104 N,汽车匀速拉绳子时的拉力F=2×103 N,汽车受到的阻力为车重的。
(1)若汽车运动的速度为1.2 m/s,则将物体由井底拉至井口,需要多长时间
(2)滑轮组的机械效率是多少 (保留一位小数)
(3)汽车的牵引力是多大
(4)将物体由井底拉至井口,汽车的牵引力做的功是多少
20.如图所示,小明用细绳系在轻质杠杆的O点将轻杆悬挂起来,在杆的A端悬挂质量为20 kg的重物,在B端竖直向下缓慢拉动杠杆至水平位置。已知AO长1 m,OB长0.5 m,小明的重力为500 N,求此时:(g取10 N/kg)
(1)重物的重力。
(2)小明对杆的拉力大小。
(3)小明用此杠杆最多能抬起物体的最大重力。
【详解答案】
1.B 解析:省力杠杆的动力臂大于阻力臂,可以省力但是费距离,羊角锤、铡刀、开瓶器等简单机械是省力杠杆,A、C、D不符合题意;费力杠杆的动力臂小于阻力臂,费力但是省距离,镊子属于费力杠杆,B符合题意。故选B。
2.B 解析:有用功与总功的比值叫作机械效率,故机械效率与做功的多少无直接联系,A错误;功率反映做功的快慢,功率大则做功快,功率小则做功慢,故B正确;机械效率与机械功率之间没有直接关系,故C错误;做功多少不确定的情况下,功率大的机器做功时间不一定短,故D错误。故选B。
3.B 解析:当秤盘放100 g物体、秤砣移到B点时,秤杆再次水平平衡,则B点所示的质量为100 g,在O点与B点两条刻线之间均匀地画上49条刻度线,则从O点到B点共50个小格,每一小格表示的质量为m0==2 g,故A错误;称中药时B端翘起,杆秤不能水平平衡,说明物体的质量大于秤砣指示的示数,可以向右侧移动秤砣,也可以减少物体的质量来使杆秤恢复水平平衡,故B正确;根据G=mg和杠杆的平衡条件可得,m物g×OA=
m砣g×OB,秤砣磨损了,则m砣减小,故OB变大,秤砣需向右移动才能使杆秤平衡,则测量结果将偏大,故C错误;若将提纽移到O点右侧,测量相同质量的物体时,左边力臂变大,右边力臂减小,秤砣质量不变,则能称量的物体质量减小,杆秤量程变小,故D错误。故选B。
4.B 解析:设动力臂为l2,杠杆长为l(即阻力臂为l);由图可知,F2与杠杆垂直,因此其力臂为最长的动力臂,由杠杆的平衡条件可知,F2为最小的动力,则F1>F2,故A错误,B正确;用力F2使杠杆在水平位置保持平衡时,由杠杆平衡条件可得,F2·l2=G·l,由图知,l2G,故C错误;因为F1>F2,F2>G,所以F1>F2>G,故D错误。故选B。
5.A 解析:A.桔槔平衡时,FA×OA=FB×OB,FB===200 N,则G桶+G水=FB=200 N,因为存在桶的重力,所以G水≠200 N,则V水≠2×10-2 m3,故A错误;B.一根硬棒能绕固定点转动,这根硬棒就是杠杆,故桔槔是杠杆装置,故B正确;C.桔槔平衡时,FA×OA=FB×OB,==,故C正确;D.把拗石的拉力看成动力,悬挂点A向远离O点的方向移动,可以增大动力臂,动力与动力臂的乘积变大,根据杠杆平衡条件,阻力与阻力臂的乘积也变大,而阻力臂不变,所以阻力变大,可以提取更多的水,故D正确。故选A。
6.C 解析:不计机械重和摩擦,设物体的重力为G。A.由图知,F1×4 m=G×2 m,所以F1=G,可以省力;B.由图知,滑轮组中由三段绳子承担物重,所以F2=G,可以省力;C.由图知,该装置是定滑轮,F3=G,不能省力;D.根据杠杆的平衡条件可得,F4×(l+2l)=G×l,所以F4=G,可以省力。由以上分析得,只有C不省力。故选C。
7.C 解析:由图可知,甲方式由两个定滑轮组成,定滑轮的本质是等臂杠杆,不能省力,故A错误;乙方式是用一个动滑轮和一个定滑轮组成的滑轮组,不仅可以省力,也可以改变力的方向,故B错误;由题可知,甲、乙两滑轮组均将相同货物提升相同高度,由W有用=Gh可知,W甲有用=W乙有用,故C正确;由图可知,甲方式由两个定滑轮组成,乙方式是用一个动滑轮和一个定滑轮组成的滑轮组,乙方式要克服动滑轮的重力做功,做的额外功大于甲方式,有用功相同、总功不相同,根据η=可知,两个滑轮组的机械效率不相等,故D错误。故选C。
8.D 解析:根据动滑轮的特点,拉力F的大小为10 N,所以重物A的重力为×10 N=5 N;重物A上升的速度为0.2 m/s,则力F上升的速度是×0.2 m/s=0.1 m/s。故选D。
9.B 解析:忽略绳重及一切阻力,用图甲绕法匀速提升重为900 N的物体时,机械效率为90%,图甲中的n=2,由η====可得,拉力F1===500 N,故A错误;图甲中,根据F1=(G+G动)可得,动滑轮的重力G动=2F1-G=2×500 N-900 N=100 N;忽略绳重及一切阻力,滑轮组的机械效率η===,则用图乙绕法匀速提升400 N的物体时,其机械效率为η'===80%,故B正确;由η===可知,分别用两种绕法匀速提升相同的物体时,η甲=η乙,故C错误;分别用两种绕法匀速提升相同物体升高相同高度时,做的有用功相同,额外功相同,则总功相同(即F1和F2做功相同),故D错误。故选B。
10.C 解析:由图可知,这个滑轮组由一个定滑轮和一个动滑轮组成,承担摩擦力的绳子段数n=2,根据滑轮组机械效率的计算公式,有η===,物体匀速运动,则FA=f,因而有η=。故选C。
11.更重些 解析:由图可知,A端胡萝卜的重心到支点O的距离(即力臂lA)比B端胡萝卜的重心到支点O的距离,(即力臂lB)小,lAGB,即A端胡萝卜比B端胡萝卜更重些。
12.小于 如图所示:
向右盘放入少量小米(合理即可)
解析:由图可知,大米对直尺的压力的力臂大于小米对直尺的压力的力臂,根据杠杆的平衡条件可知,大米的重力小于小米的重力,由G=mg可知,大米的质量小于小米的质量。从支点O向F的作用线作垂线段l,即为力F的力臂l。现向左盘中再加入少量大米,则左边力与力臂的乘积变大,为使直尺恢复平衡,可向右盘放入少量小米或将左盘向右移动一段距离等。
13.400 60% 解析:由图乙可知,当建材重力G1=400 N时,η1=50%,由η=====50%可得,此时拉力为F1===400 N,滑轮和钢绳的摩擦力及绳重忽略不计,因为拉力F=(G+G动),所以动滑轮的重力G动=2F1-G1=2×400 N-400 N=400 N。60 kg建材的重力G=mg=60 kg×10 N/kg=600 N,运送建材的质量为60 kg时,滑轮组的机械效率为η=====60%。
14.等于 小于 小于 大于 解析:因为W有用=Gh,所以利用甲和乙滑轮组将同一重物提升相同高度做的有用功相等,即W有用甲=W有用乙;不计绳重及摩擦时,提升动滑轮做的功是额外功,甲图中只有一个动滑轮,乙图中有两个动滑轮,提升相同高度,由W额外=G轮h可知,W额外甲η乙。
15.(1)(2)如图所示:
甲 乙
解析:(1)动力F1最小时,其力臂最长,即从支点到动力作用点的距离为力臂l;力和力臂是垂直关系,故在A点作力臂l的垂线,方向向上,即为最小动力F1。(2)用3段绳子承担物重,绳端拉力向上,绕法如上图。
16.(1)右 (2)2 (3)等于 (4)0 (5)2
解析:(1)实验前,杠杆静止时如图甲所示,左边重,此时应将杠杆的平衡螺母向右调节。(2)根据杠杆的平衡条件,则3G×2l=nG×3l,解得n=2,所以在杠杆右边B点处挂2个同样的钩码。(3)将B点所挂钩码取下,用弹簧测力计倒挂在B点并竖直向下拉,使杠杆水平平衡,阻力与阻力臂的乘积不变,动力臂的大小不变,则动力不变,此时弹簧测力计的示数等于B点原本所挂钩码重力的大小。(4)若提起提纽1,秤盘不放物体,将秤砣移至某一点使杆秤恰好水平平衡,此时秤盘内的质量为零,那么该点标定的刻度应为0。(5)选用提纽2,支点左移,可以增大阻力臂,减小动力臂,秤砣的质量不变,阻力的大小不变,阻力与阻力臂的乘积变大,则动力会变大,增加了称量的范围。
17.(1)匀速 (2)丙 80% (3)错误 (4)1、2 (5)越低
解析:(1)实验时,应缓慢匀速拉动弹簧测力计,此时钩码受力平衡,测力计的示数等于拉力。(2)由表中数据可得,第3次实验时钩码移动的距离为0.1 m,绳子端移动的距离为0.4 m,则绳子的股数为n==4,即动滑轮上有4股绳,所以图丙装置符合题意。由表中数据可得,有用功为W有用=G3h3=4 N×0.1 m=0.4 J,总功为W总=F3s3=1.25 N×
0.4 m=0.5 J,机械效率为η===80%。(3)对比2、4两次实验数据发现,其他条件不变,只改变钩码提升的高度,机械效率是不变的,所以猜想Ⅰ是错误的。(4)要想得到同一滑轮组提升重物时,物重越大,滑轮组的机械效率越高的结论,需要保证所用滑轮组不变,重物提升的高度也不变,只改变重物的重力,所以表中1、2两次实验符合条件。(5)对比2、3两次实验数据可以发现,第2次实验是用乙装置完成的,第3次实验是用丙装置完成的,重物的重力不变,提升的高度也不变,但滑轮组中动滑轮的个数增多了,且机械效率降低,所以可得结论:不同滑轮组提升相同重物时,动滑轮越重,滑轮组的机械效率越低。
18.(1)50% 0.9 (2)斜面越陡,其机械效率越高 (3)盘山公路(合理即可)
解析:(1)第2次实验中,斜面的机械效率:η====50%。在第2次实验中,有用功W有用=Gh=3 N×
0.3 m=0.9 J,总功W总=Fs=1.8 N×1 m=1.8 J,额外功W额外=W总-W有用=1.8 J-0.9 J=0.9 J,根据W额外=fs可得,摩擦力f===0.9 N。(2)由表中数据可知,斜面越陡,其机械效率越高。(3)生活中利用斜面的实例:盘山公路、螺丝钉等。
19.解:(1)由图可知,滑轮组中由3段绳子承担物重,则物体上升的速度:
v物=v车=×1.2 m/s=0.4 m/s,
将物体由井底拉至井口需要的时间:
t===25 s。
(2)滑轮组的机械效率:
η=====≈66.7%。
(3)由题意可得,汽车受到的阻力:
f=G车=×3×104 N=1 500 N。
汽车做匀速直线运动,受到平衡力的作用,在水平方向上,汽车受到向右的牵引力、向左的拉力、向左的阻力的作用;由力的平衡条件可得,牵引力:F牵=F+f=2×103 N+1 500 N=3 500 N。
(4)将物体拉至井口,汽车运动的距离:s车=s绳=3h=3×10 m=30 m,
牵引力做功:W=F牵s车=3 500 N×30 m=1.05×105 J。
答:(1)若汽车的运动速度为1.2 m/s,将物体由井底拉至井口,需要25 s;
(2)滑轮组的机械效率是66.7%;
(3)汽车的牵引力是3 500 N;
(4)将物体由井底拉至井口,汽车的牵引力做的功是1.05×105 J。
20.解:(1)重物的重力:
G=mg=20 kg×10 N/kg=200 N。
(2)根据杠杆的平衡条件可得
FA×OA=FB×OB,
小明对杆的拉力:
FB===400 N。
(3)小明拉起重物最重时,小明对地面的压力正好为零,此时小明对杠杆的拉力等于小明的重力,即
FB'=G人=500 N,
根据杠杆平衡条件可得
FA'×OA=FB'×OB,
即FA'===250 N。
答:(1)重物的重力为200 N;
(2)小明对杆的拉力为400 N;
(3)小明用此杆最多能抬起物体的最大重力为250 N。
(满分:100分 时间:60分钟)
一、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项最符合题意)
1.在如图所示的简单机械中,属于费力杠杆的是 ( )
A.羊角锤 B.镊子 C.铡刀 D.开瓶器
2.下列关于功、功率、机械效率的说法正确的是 ( )
A.做功多的机器机械效率一定高
B.功率小的机器做功慢
C.机械效率高的机械功率一定大
D.功率大的机器做功时间一定短
3.(2024重庆A卷中考)同学们模仿中药房的戥秤制作杆秤,用筷子做秤杆,用钩码做秤砣,用细线将秤盘系在A点。当不挂秤砣、且秤盘不放物体时,在O点提起提纽,秤杆水平平衡;当秤盘放
100 g物体、秤砣移到B点时,秤杆再次水平平衡,如图所示。在O点与B点两条刻线之间均匀地画上49条刻度线。下列说法正确的是 ( )
A.自制杆秤的每一格约表示2.08 g
B.称中药时B端翘起应减少中药恢复水平平衡
C.若秤砣磨损,则测量结果会比真实质量偏小
D.若将提纽移到O点右侧可以增大杆秤的量程
4.如图所示,O点为杠杆的支点,杠杆右端挂有重为G的物体,杠杆在力F1的作用下在水平位置平衡。如果用力F2代替力F1使杠杆仍在水平位置保持平衡,下列关系中正确的是( )
A.F1
C.F2
A.桔槔平衡时,桶内水的体积为2×10-2 m3
B.桔槔是杠杆装置
C.桔槔平衡时,A、B两点所受的拉力之比为1∶2
D.要想一次提取更多的水,可以将悬挂点A向远离O点的方向移动
6.简单机械在我们生活中的应用很广泛。下图是使用简单机械匀速提升同一物体的四种方式(不计机械重和摩擦),其中不省力的是 ( )
A B C D
7.如图所示,快递小哥为了把较重的货物装入运输车,用同样的器材设计了甲、乙两种方式提升货物。若把同一货物匀速提升到同一高度,忽略绳重和摩擦。下列分析正确的是 ( )
甲 乙
A.甲方式可以省力 B.乙方式不能改变力的方向
C.甲、乙两种方式做的有用功相等 D.甲、乙两种方式的机械效率相等
8.如图所示,在竖直向上大小为10 N的力F的作用下,重物A沿竖直方向匀速上升。已知重物A的上升速度为0.2 m/s,不计滑轮重、绳重及绳与滑轮间的摩擦,则重物A的重力大小和滑轮上升的速度分别为 ( )
A.20 N,0.4 m/s B.20 N,0.1 m/s C.5 N,0.4 m/s D.5 N,0.1 m/s
9.如图所示,甲、乙分别为同一滑轮组的不同绕法,忽略绳重及一切阻力,用图甲绕法匀速提升重为900 N的物体时,机械效率为90%。下列判断正确的是 ( )
甲 乙
A.拉力F1的大小为450 N
B.用图乙绕法匀速提升400 N的物体时,机械效率为80%
C.分别用两种绕法匀速提升相同的物体时,图乙绕法的机械效率大
D.分别用两种绕法匀速提升相同物体升高相同高度,F2做功少
10.如图所示,利用轻质滑轮组匀速拉动水平地面上重为G的物体。若拉力的大小为F,物体和地面之间的摩擦力大小为f,A点的拉力为FA,则下列滑轮组的机械效率表达式正确的是 ( )
A. B. C. D.
二、填空及作图题(本大题共5小题,每空2分,每图2分,共24分)
11.学习了杠杆知识后,小明将一个胡萝卜分成了两部分,如图所示,根据杠杆平衡的条件可得出A端胡萝卜相比B端胡萝卜 (选填“更重些”“一样重”或“更轻些”)。
12.在均匀直尺的中央挖一小凹槽,把一个薄金属片的一端插入橡皮中,另一端支在直尺的凹槽内制成一个简易“天平”。静止时直尺水平平衡。在直尺的两侧各放一个相同的小盘,在小盘中倒入质量不等的大米和小米,调整小盘在直尺上的位置,使直尺再次水平平衡,如图所示。由图可知,大米的质量 (选填“大于”或“小于”)小米的质量。F是左盘对直尺施加的力,请在图中画出F的力臂。现向左盘中再加入少量大米,写出一种能够使直尺恢复平衡的方法: 。
13.工人用如图甲所示的滑轮组运送建材上楼,每次运送量不定。滑轮组的机械效率η随建材重力G变化的图像如图乙所示,钢绳和滑轮的摩擦力及绳重均可以忽略不计,则动滑轮的重力为
N;若某次运送建材的质量为60 kg,滑轮组的机械效率是 。(g取10 N/kg)
甲 乙
14.用如图甲、乙所示的两种方式将同一重物匀速提升相同高度。图中所有滑轮等重,且不计绳重和摩擦。在重物上升过程中,甲的有用功 乙的有用功,甲的额外功 乙的额外功,甲的总功 乙的总功,甲的机械效率 乙的机械效率。(均选填“大于”“等于”或“小于”)
甲 乙
15.按要求作图:
(1)如图甲所示,为了让杠杆静止在图中位置,请作出在A点所施加的最小动力F1的示意图。
(2)如图乙所示,某人站在A点处用一根绳子和两个滑轮提起物体B,画出最省力的绕线。
甲 乙
三、实验探究题(本大题共3小题,第16小题10分,第17小题12分,第18小题8分,共30分)
16.杆秤是我国最古老也是现今人们仍然在使用的称量工具,是根据杠杆原理制造出来的,以方便人们买卖,映射出中国古代劳动人民的聪明才智,具有悠久的历史。在物理实践活动中,小红在探究杠杆的平衡条件后制作了一把杆秤。
甲 乙 丙
(1)实验前,杠杆静止时如图甲所示,此时应将杠杆的平衡螺母向 调,直至杠杆在水平位置平衡。
(2)杠杆水平平衡后,在杠杆左边A点处挂3个相同的钩码,如图乙所示,要使杠杆平衡,应在杠杆右边B点处挂 个同样的钩码。
(3)小红想用弹簧测力计进行实验,将B点所挂钩码取下,用弹簧测力计倒挂在B点并竖直向下拉,使杠杆水平平衡,此时弹簧测力计的示数将 (选填“大于”“小于”或“等于”)B点原本所挂钩码重力的大小。
(4)实验结束后,小红制作了如图丙所示的杆秤,该杆秤有2个提纽。若提起提纽1,秤盘不放物体,将秤砣移至某一点使杆秤恰好水平平衡,那么该点标定的刻度应为 ;以此类推,在秤盘上放1 g的物体,移动秤砣,使杆秤在水平位置处于平衡状态,在秤砣所挂的位置标定的刻度为1;然后在秤盘上放2 g的物体按上述方法直至标出所有刻度。
(5)若要增加称量的范围,应选用提纽 。
17.提高机械效率可以充分发挥机械设备的作用,对节能减排、提高经济效益有重要的意义。某科技创新小组根据生活经验和客观事实,对影响滑轮组机械效率的因素作出如下猜想:
猜想I:滑轮组的机械效率与物体被提升的高度有关;
猜想Ⅱ:滑轮组的机械效率与动滑轮的重力有关;
猜想Ⅲ:滑轮组的机械效率与所提物体的重力有关。
根据猜想,运用图甲、乙、丙所示的装置进行了实验探究,测得的实验数据如下表所示。
甲 乙 丙
实验 次数 钩码的 重力G/N 钩码上升 高度h/m 绳端拉力 F/N 绳端移动 的距离s/m 机械 效率η
1 2 0.1 0.90 0.3 74.1%
2 4 0.1 1.50 0.3 88.9%
3 4 0.1 1.25 0.4
4 4 0.2 1.50 0.6 88.9%
(1)实验时应沿竖直方向 缓慢向上拉动弹簧测力计。
(2)分析表中数据可知:第3次实验是利用图 装置完成的,它的机械效率η= 。
(3)比较2、4两次实验数据,可验证猜想I是 (选填“正确”或“错误”)的。
(4)通过比较 (填实验序号)两次实验数据可得出结论:同一滑轮组提升重物时,物重越大,滑轮组的机械效率越高。
(5)通过比较2、3两次实验数据可得出结论:不同滑轮组提升相同重物时,动滑轮越重,滑轮组的机械效率 。
18.为了探究斜面的机械效率与斜面倾斜程度之间的关系,探究小组的同学利用木板、刻度尺、弹簧测力计、木块等器材设计了如图所示的实验装置,实验测得的数据如下表:
实验 次数 斜面倾 斜程度 木块重 力G/N 斜面高 度h/m 沿斜面拉 力F/N 斜面长 度s/m 机械 效率
1 较缓 3 0.2 1.6 1 37.5%
2 较陡 3 0.3 1.8 1
3 最陡 3 0.4 2.0 1 60%
请你根据表中的数据回答下列问题:
(1)第2次实验中,斜面的机械效率为 ,斜面对木块的摩擦力为 N。
(2)斜面的机械效率与斜面的倾斜程度之间的关系是 。
(3)试列举出生活中利用斜面的一个实例: 。
四、计算应用题(本大题共2小题,第19小题8分,第20小题8分,共16分。解答时,要求有必要的文字说明、公式和计算步骤等,只写最后结果不得分)
19.如图是一辆汽车通过滑轮组将深井中的物体拉至井口的装置图,已知井深10 m,物体重G=4×103 N,汽车重G车=3×104 N,汽车匀速拉绳子时的拉力F=2×103 N,汽车受到的阻力为车重的。
(1)若汽车运动的速度为1.2 m/s,则将物体由井底拉至井口,需要多长时间
(2)滑轮组的机械效率是多少 (保留一位小数)
(3)汽车的牵引力是多大
(4)将物体由井底拉至井口,汽车的牵引力做的功是多少
20.如图所示,小明用细绳系在轻质杠杆的O点将轻杆悬挂起来,在杆的A端悬挂质量为20 kg的重物,在B端竖直向下缓慢拉动杠杆至水平位置。已知AO长1 m,OB长0.5 m,小明的重力为500 N,求此时:(g取10 N/kg)
(1)重物的重力。
(2)小明对杆的拉力大小。
(3)小明用此杠杆最多能抬起物体的最大重力。
【详解答案】
1.B 解析:省力杠杆的动力臂大于阻力臂,可以省力但是费距离,羊角锤、铡刀、开瓶器等简单机械是省力杠杆,A、C、D不符合题意;费力杠杆的动力臂小于阻力臂,费力但是省距离,镊子属于费力杠杆,B符合题意。故选B。
2.B 解析:有用功与总功的比值叫作机械效率,故机械效率与做功的多少无直接联系,A错误;功率反映做功的快慢,功率大则做功快,功率小则做功慢,故B正确;机械效率与机械功率之间没有直接关系,故C错误;做功多少不确定的情况下,功率大的机器做功时间不一定短,故D错误。故选B。
3.B 解析:当秤盘放100 g物体、秤砣移到B点时,秤杆再次水平平衡,则B点所示的质量为100 g,在O点与B点两条刻线之间均匀地画上49条刻度线,则从O点到B点共50个小格,每一小格表示的质量为m0==2 g,故A错误;称中药时B端翘起,杆秤不能水平平衡,说明物体的质量大于秤砣指示的示数,可以向右侧移动秤砣,也可以减少物体的质量来使杆秤恢复水平平衡,故B正确;根据G=mg和杠杆的平衡条件可得,m物g×OA=
m砣g×OB,秤砣磨损了,则m砣减小,故OB变大,秤砣需向右移动才能使杆秤平衡,则测量结果将偏大,故C错误;若将提纽移到O点右侧,测量相同质量的物体时,左边力臂变大,右边力臂减小,秤砣质量不变,则能称量的物体质量减小,杆秤量程变小,故D错误。故选B。
4.B 解析:设动力臂为l2,杠杆长为l(即阻力臂为l);由图可知,F2与杠杆垂直,因此其力臂为最长的动力臂,由杠杆的平衡条件可知,F2为最小的动力,则F1>F2,故A错误,B正确;用力F2使杠杆在水平位置保持平衡时,由杠杆平衡条件可得,F2·l2=G·l,由图知,l2
5.A 解析:A.桔槔平衡时,FA×OA=FB×OB,FB===200 N,则G桶+G水=FB=200 N,因为存在桶的重力,所以G水≠200 N,则V水≠2×10-2 m3,故A错误;B.一根硬棒能绕固定点转动,这根硬棒就是杠杆,故桔槔是杠杆装置,故B正确;C.桔槔平衡时,FA×OA=FB×OB,==,故C正确;D.把拗石的拉力看成动力,悬挂点A向远离O点的方向移动,可以增大动力臂,动力与动力臂的乘积变大,根据杠杆平衡条件,阻力与阻力臂的乘积也变大,而阻力臂不变,所以阻力变大,可以提取更多的水,故D正确。故选A。
6.C 解析:不计机械重和摩擦,设物体的重力为G。A.由图知,F1×4 m=G×2 m,所以F1=G,可以省力;B.由图知,滑轮组中由三段绳子承担物重,所以F2=G,可以省力;C.由图知,该装置是定滑轮,F3=G,不能省力;D.根据杠杆的平衡条件可得,F4×(l+2l)=G×l,所以F4=G,可以省力。由以上分析得,只有C不省力。故选C。
7.C 解析:由图可知,甲方式由两个定滑轮组成,定滑轮的本质是等臂杠杆,不能省力,故A错误;乙方式是用一个动滑轮和一个定滑轮组成的滑轮组,不仅可以省力,也可以改变力的方向,故B错误;由题可知,甲、乙两滑轮组均将相同货物提升相同高度,由W有用=Gh可知,W甲有用=W乙有用,故C正确;由图可知,甲方式由两个定滑轮组成,乙方式是用一个动滑轮和一个定滑轮组成的滑轮组,乙方式要克服动滑轮的重力做功,做的额外功大于甲方式,有用功相同、总功不相同,根据η=可知,两个滑轮组的机械效率不相等,故D错误。故选C。
8.D 解析:根据动滑轮的特点,拉力F的大小为10 N,所以重物A的重力为×10 N=5 N;重物A上升的速度为0.2 m/s,则力F上升的速度是×0.2 m/s=0.1 m/s。故选D。
9.B 解析:忽略绳重及一切阻力,用图甲绕法匀速提升重为900 N的物体时,机械效率为90%,图甲中的n=2,由η====可得,拉力F1===500 N,故A错误;图甲中,根据F1=(G+G动)可得,动滑轮的重力G动=2F1-G=2×500 N-900 N=100 N;忽略绳重及一切阻力,滑轮组的机械效率η===,则用图乙绕法匀速提升400 N的物体时,其机械效率为η'===80%,故B正确;由η===可知,分别用两种绕法匀速提升相同的物体时,η甲=η乙,故C错误;分别用两种绕法匀速提升相同物体升高相同高度时,做的有用功相同,额外功相同,则总功相同(即F1和F2做功相同),故D错误。故选B。
10.C 解析:由图可知,这个滑轮组由一个定滑轮和一个动滑轮组成,承担摩擦力的绳子段数n=2,根据滑轮组机械效率的计算公式,有η===,物体匀速运动,则FA=f,因而有η=。故选C。
11.更重些 解析:由图可知,A端胡萝卜的重心到支点O的距离(即力臂lA)比B端胡萝卜的重心到支点O的距离,(即力臂lB)小,lA
12.小于 如图所示:
向右盘放入少量小米(合理即可)
解析:由图可知,大米对直尺的压力的力臂大于小米对直尺的压力的力臂,根据杠杆的平衡条件可知,大米的重力小于小米的重力,由G=mg可知,大米的质量小于小米的质量。从支点O向F的作用线作垂线段l,即为力F的力臂l。现向左盘中再加入少量大米,则左边力与力臂的乘积变大,为使直尺恢复平衡,可向右盘放入少量小米或将左盘向右移动一段距离等。
13.400 60% 解析:由图乙可知,当建材重力G1=400 N时,η1=50%,由η=====50%可得,此时拉力为F1===400 N,滑轮和钢绳的摩擦力及绳重忽略不计,因为拉力F=(G+G动),所以动滑轮的重力G动=2F1-G1=2×400 N-400 N=400 N。60 kg建材的重力G=mg=60 kg×10 N/kg=600 N,运送建材的质量为60 kg时,滑轮组的机械效率为η=====60%。
14.等于 小于 小于 大于 解析:因为W有用=Gh,所以利用甲和乙滑轮组将同一重物提升相同高度做的有用功相等,即W有用甲=W有用乙;不计绳重及摩擦时,提升动滑轮做的功是额外功,甲图中只有一个动滑轮,乙图中有两个动滑轮,提升相同高度,由W额外=G轮h可知,W额外甲
15.(1)(2)如图所示:
甲 乙
解析:(1)动力F1最小时,其力臂最长,即从支点到动力作用点的距离为力臂l;力和力臂是垂直关系,故在A点作力臂l的垂线,方向向上,即为最小动力F1。(2)用3段绳子承担物重,绳端拉力向上,绕法如上图。
16.(1)右 (2)2 (3)等于 (4)0 (5)2
解析:(1)实验前,杠杆静止时如图甲所示,左边重,此时应将杠杆的平衡螺母向右调节。(2)根据杠杆的平衡条件,则3G×2l=nG×3l,解得n=2,所以在杠杆右边B点处挂2个同样的钩码。(3)将B点所挂钩码取下,用弹簧测力计倒挂在B点并竖直向下拉,使杠杆水平平衡,阻力与阻力臂的乘积不变,动力臂的大小不变,则动力不变,此时弹簧测力计的示数等于B点原本所挂钩码重力的大小。(4)若提起提纽1,秤盘不放物体,将秤砣移至某一点使杆秤恰好水平平衡,此时秤盘内的质量为零,那么该点标定的刻度应为0。(5)选用提纽2,支点左移,可以增大阻力臂,减小动力臂,秤砣的质量不变,阻力的大小不变,阻力与阻力臂的乘积变大,则动力会变大,增加了称量的范围。
17.(1)匀速 (2)丙 80% (3)错误 (4)1、2 (5)越低
解析:(1)实验时,应缓慢匀速拉动弹簧测力计,此时钩码受力平衡,测力计的示数等于拉力。(2)由表中数据可得,第3次实验时钩码移动的距离为0.1 m,绳子端移动的距离为0.4 m,则绳子的股数为n==4,即动滑轮上有4股绳,所以图丙装置符合题意。由表中数据可得,有用功为W有用=G3h3=4 N×0.1 m=0.4 J,总功为W总=F3s3=1.25 N×
0.4 m=0.5 J,机械效率为η===80%。(3)对比2、4两次实验数据发现,其他条件不变,只改变钩码提升的高度,机械效率是不变的,所以猜想Ⅰ是错误的。(4)要想得到同一滑轮组提升重物时,物重越大,滑轮组的机械效率越高的结论,需要保证所用滑轮组不变,重物提升的高度也不变,只改变重物的重力,所以表中1、2两次实验符合条件。(5)对比2、3两次实验数据可以发现,第2次实验是用乙装置完成的,第3次实验是用丙装置完成的,重物的重力不变,提升的高度也不变,但滑轮组中动滑轮的个数增多了,且机械效率降低,所以可得结论:不同滑轮组提升相同重物时,动滑轮越重,滑轮组的机械效率越低。
18.(1)50% 0.9 (2)斜面越陡,其机械效率越高 (3)盘山公路(合理即可)
解析:(1)第2次实验中,斜面的机械效率:η====50%。在第2次实验中,有用功W有用=Gh=3 N×
0.3 m=0.9 J,总功W总=Fs=1.8 N×1 m=1.8 J,额外功W额外=W总-W有用=1.8 J-0.9 J=0.9 J,根据W额外=fs可得,摩擦力f===0.9 N。(2)由表中数据可知,斜面越陡,其机械效率越高。(3)生活中利用斜面的实例:盘山公路、螺丝钉等。
19.解:(1)由图可知,滑轮组中由3段绳子承担物重,则物体上升的速度:
v物=v车=×1.2 m/s=0.4 m/s,
将物体由井底拉至井口需要的时间:
t===25 s。
(2)滑轮组的机械效率:
η=====≈66.7%。
(3)由题意可得,汽车受到的阻力:
f=G车=×3×104 N=1 500 N。
汽车做匀速直线运动,受到平衡力的作用,在水平方向上,汽车受到向右的牵引力、向左的拉力、向左的阻力的作用;由力的平衡条件可得,牵引力:F牵=F+f=2×103 N+1 500 N=3 500 N。
(4)将物体拉至井口,汽车运动的距离:s车=s绳=3h=3×10 m=30 m,
牵引力做功:W=F牵s车=3 500 N×30 m=1.05×105 J。
答:(1)若汽车的运动速度为1.2 m/s,将物体由井底拉至井口,需要25 s;
(2)滑轮组的机械效率是66.7%;
(3)汽车的牵引力是3 500 N;
(4)将物体由井底拉至井口,汽车的牵引力做的功是1.05×105 J。
20.解:(1)重物的重力:
G=mg=20 kg×10 N/kg=200 N。
(2)根据杠杆的平衡条件可得
FA×OA=FB×OB,
小明对杆的拉力:
FB===400 N。
(3)小明拉起重物最重时,小明对地面的压力正好为零,此时小明对杠杆的拉力等于小明的重力,即
FB'=G人=500 N,
根据杠杆平衡条件可得
FA'×OA=FB'×OB,
即FA'===250 N。
答:(1)重物的重力为200 N;
(2)小明对杆的拉力为400 N;
(3)小明用此杆最多能抬起物体的最大重力为250 N。
