第十章 浮力 专题训练六 利用浮力测密度 同步练 (含答案)2024-2025学年物理人教版八年级下册
文档属性
| 名称 | 第十章 浮力 专题训练六 利用浮力测密度 同步练 (含答案)2024-2025学年物理人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 182.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-15 21:56:19 | ||
图片预览

文档简介
专题训练六 利用浮力测密度
利用浮沉条件测密度
1.用量筒测固体的密度(固体密度小于水且不吸水,水的密度用ρ水表示),方案如图所示。
① ② ③
(1)在量筒内装适量的水,读取量筒示数为V1。
(2)将固体放入量筒内,读取量筒示数为V2。
(3)用细铁丝或大头针将固体压至 于水中,读取量筒示数为V3。
(4)固体的质量m= ,固体的体积V= 。
(5)固体的密度ρ= 。
2.小明捡到一颗漂亮的小石块,他想估测出小石块的密度ρ石,回家后他利用一把刻度尺、一条细线、一个厚底薄壁圆柱形杯子(杯子厚度不计)和一桶水来测这颗小石块的密度。下面是小明测出ρ石的部分实验步骤,请你按照小明的实验思路,将实验步骤补充完整。
甲 乙
(1)将装有适量水的长杯子放入桶内的水中,使杯子 在水面上,如图甲所示,用刻度尺测出杯底到桶中水面的高度记为h1。
(2)用刻度尺测得杯底到杯内水面的高度记为h2。
(3)把小石块投入杯内水中,杯子继续竖直漂浮在水面上,如图乙所示, 。
(4) 。
(5)接着他将杯子取出,测得杯子的底面积为S。
(6)利用上述测量出的物理量和题中的已知量计算ρ石的表达式为 。
3.小桂分享他在家仅用电子秤、碗和水(已知水的密度为ρ水),测量蜡块的密度的方法:
图1 图2 图3
①如图1,用电子秤测出某圆柱体蜡块的质量为m1;
②如图2,将蜡块放入水中,静止时蜡块竖直漂浮,记下水面对应蜡块的位置;
③取出蜡块擦拭干净,并沿记号水平切下其没入水中的部分(不计损耗),称其质量为m2,如图3所示;
④结合以上测量数据算得蜡块的密度表达式为 (用m1、m2、ρ水表示)。
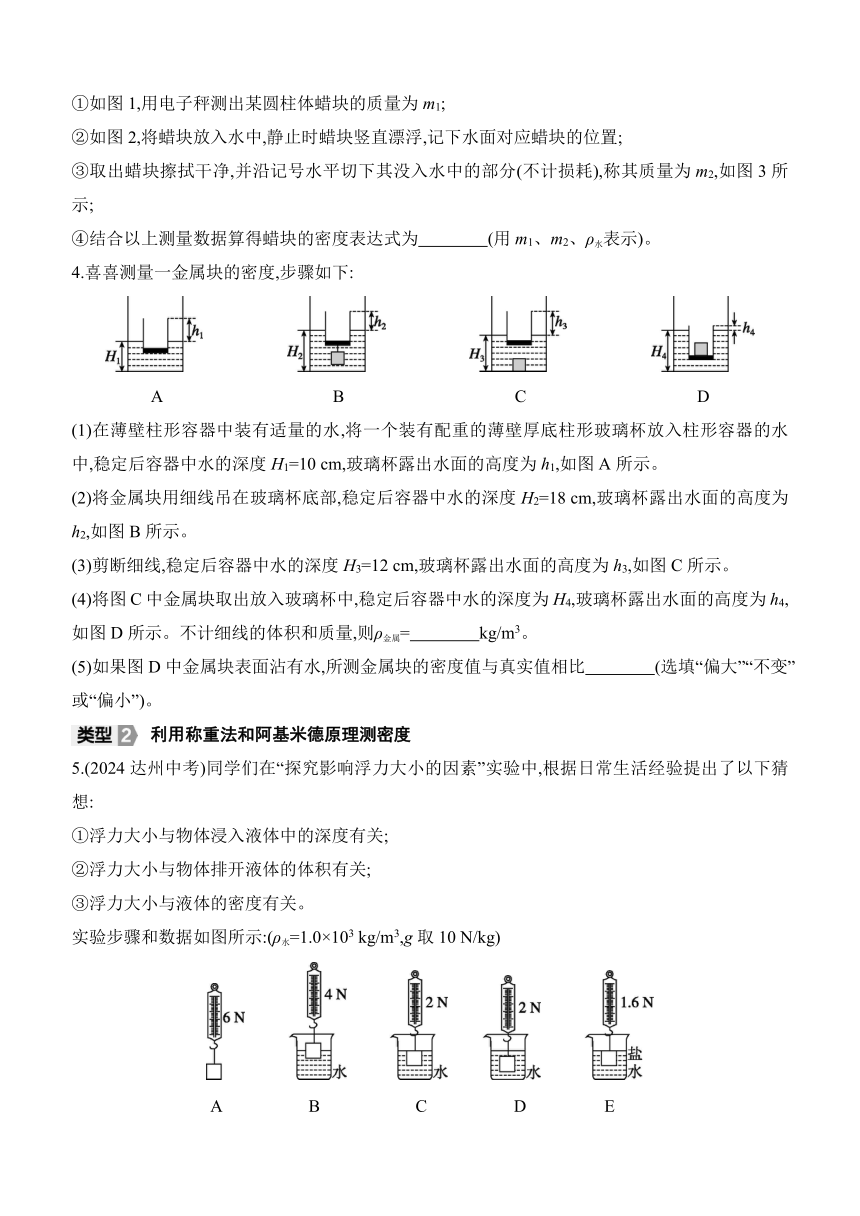
4.喜喜测量一金属块的密度,步骤如下:
A B C D
(1)在薄壁柱形容器中装有适量的水,将一个装有配重的薄壁厚底柱形玻璃杯放入柱形容器的水中,稳定后容器中水的深度H1=10 cm,玻璃杯露出水面的高度为h1,如图A所示。
(2)将金属块用细线吊在玻璃杯底部,稳定后容器中水的深度H2=18 cm,玻璃杯露出水面的高度为h2,如图B所示。
(3)剪断细线,稳定后容器中水的深度H3=12 cm,玻璃杯露出水面的高度为h3,如图C所示。
(4)将图C中金属块取出放入玻璃杯中,稳定后容器中水的深度为H4,玻璃杯露出水面的高度为h4,如图D所示。不计细线的体积和质量,则ρ金属= kg/m3。
(5)如果图D中金属块表面沾有水,所测金属块的密度值与真实值相比 (选填“偏大”“不变”或“偏小”)。
利用称重法和阿基米德原理测密度
5.(2024达州中考)同学们在“探究影响浮力大小的因素”实验中,根据日常生活经验提出了以下猜想:
①浮力大小与物体浸入液体中的深度有关;
②浮力大小与物体排开液体的体积有关;
③浮力大小与液体的密度有关。
实验步骤和数据如图所示:(ρ水=1.0×103 kg/m3,g取10 N/kg)
A B C D E
(1)根据实验数据,小聪计算出该物体浸没在水中受到的浮力大小是 N。
(2)为了验证猜想①,分析A与C、D三次实验,得出的结论是浸没在液体中的物体所受浮力大小与其浸入液体中的深度 (选填“有”或“无”)关。
(3)为了验证猜想②,分析A与 三次实验,得出的结论是浸在液体中的物体所受浮力大小与物体排开液体的体积有关。
(4)小聪为了验证猜想③,分析A与B、E三次实验,得出的结论是浸在液体中的物体所受浮力大小与液体的密度有关。你认为这样操作是 (选填“正确”或“错误”)的,理由是 。
(5)细心的小红利用实验数据还计算出步骤E中所用盐水的密度是 kg/m3。
6.物理兴趣小组的同学在探究影响浮力大小的因素过程中,经过讨论提出如下猜想:
猜想1:浮力的大小与物体浸入液体中的深度有关;
猜想2:浮力的大小与液体的密度有关;
猜想3:浮力的大小与物体的形状有关。
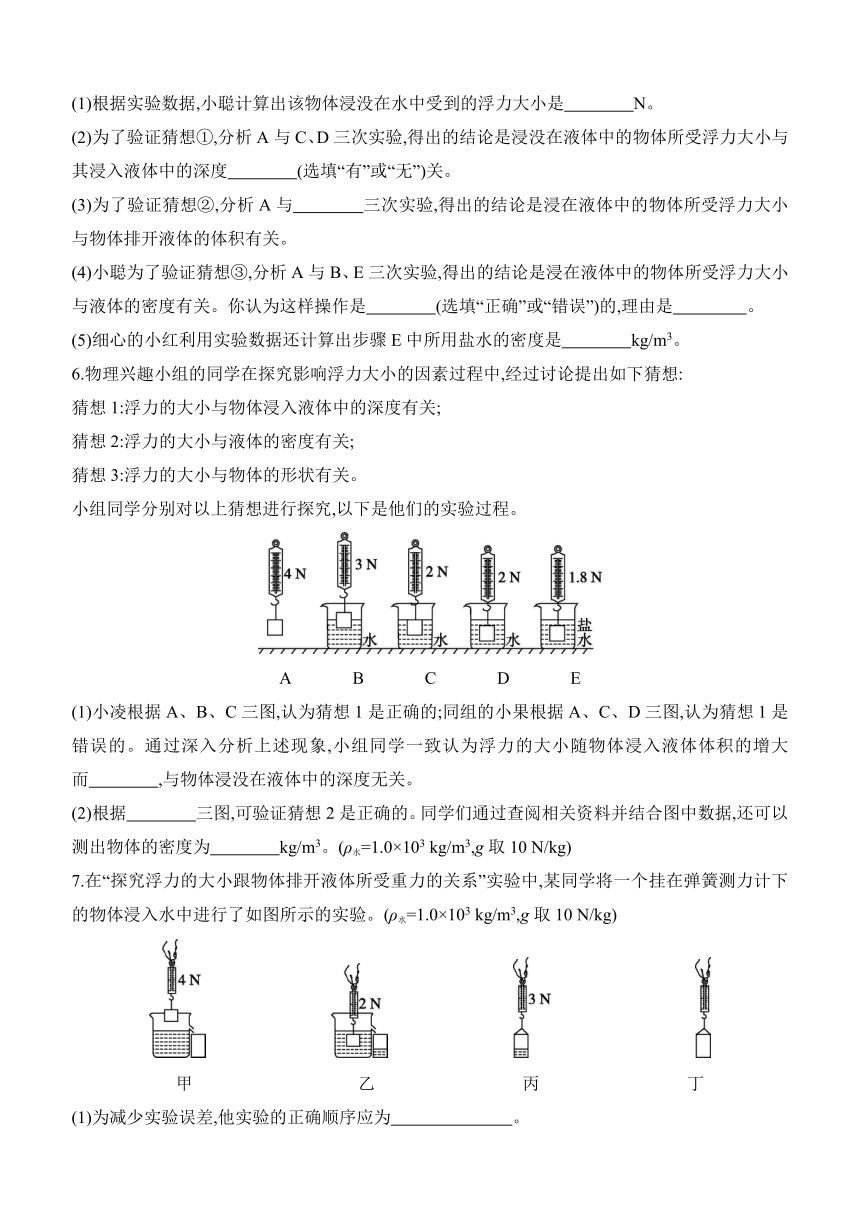
小组同学分别对以上猜想进行探究,以下是他们的实验过程。
A B C D E
(1)小凌根据A、B、C三图,认为猜想1是正确的;同组的小果根据A、C、D三图,认为猜想1是错误的。通过深入分析上述现象,小组同学一致认为浮力的大小随物体浸入液体体积的增大而 ,与物体浸没在液体中的深度无关。
(2)根据 三图,可验证猜想2是正确的。同学们通过查阅相关资料并结合图中数据,还可以测出物体的密度为 kg/m3。(ρ水=1.0×103 kg/m3,g取10 N/kg)
7.在“探究浮力的大小跟物体排开液体所受重力的关系”实验中,某同学将一个挂在弹簧测力计下的物体浸入水中进行了如图所示的实验。(ρ水=1.0×103 kg/m3,g取10 N/kg)
甲 乙 丙 丁
(1)为减少实验误差,他实验的正确顺序应为 。
(2)根据图中信息可知,物体浸没在水中时受到的浮力为 N;经计算可知,图丁中弹簧测力计的示数应为 N,物体的密度为 kg/m3。
(3)更换不同的物体和液体做实验,达到多次测量 (选填“寻找普遍规律”或“求平均值减小误差”)的目的。大量的实验结果表明,浸在液体中的物体受到向上的浮力,浮力的大小
它排开的液体所受到的重力,这就是著名的阿基米德原理。
【详解答案】
1.(3)浸没 (4)(V2-V1)ρ水 V3-V1
(5)ρ水
解析:在量筒内装适量的水,读取量筒示数为V1,将固体放入量筒内,读取量筒示数为V2,此时,固体排开水的体积为V排=V2-V1,此时,固体受到的浮力为F浮=ρ水gV排=ρ水g(V2-V1),固体处于漂浮状态,受到的浮力等于重力,即G=mg=F浮=ρ水g(V2-V1),则固体的质量为m=(V2-V1)ρ水。用细铁丝或大头针将固体压至浸没于水中,读取量筒示数为V3,此时,固体和量筒内水的总体积为V3,则固体的体积为V=V3-V1。固体的密度为ρ==ρ水。
2.(1)漂浮
(3)用刻度尺测出杯底到桶中水面的高度h3
(4)用刻度尺测出杯底到杯内水面的高度h4
(6)ρ石=
解析:(1)图甲中,将装有适量水的长杯子放入桶内的水中,使杯子漂浮在水面上。(3)把小石块投入杯内水中,杯子继续竖直漂浮在水面上,如图乙所示,小石块的重力等于杯子浮力的增加量,由G=ΔF浮=ρ水gΔV排=ρ水gS·(h3-h1)可知需要测出杯底到桶中水面的高度h3。(4)由V=S(h4-h2)可知利用排水法测量小石块体积时需要测出杯底到杯内水面的高度h4。(6)由G=mg可得,小石头的质量m=ρ水S(h3-h1),则小石头的密度ρ石===。
3. 解析:用电子秤测出某圆柱体蜡块的质量为m1,则蜡块的重力G=m1g;将蜡块放入水中,静止时蜡块竖直漂浮,则F浮=G,由阿基米德原理和浮沉条件知,ρ水gV排=m1g;解得蜡块排开水的体积:V排=,取出蜡块擦拭干净,并沿记号水平切下没入水中的部分(不计损耗),称其质量为m2,蜡块浸入水中的体积V2==V排;则有=,得蜡块的密度表达式ρ蜡=。
4.(4)4.0×103 (5)不变
解析:设容器底面积为S,玻璃杯包括配重的重力为G,由图A可知,F浮1=G,即ρ水gV排1=G,由图B可知,F浮2=G+
G金属,即ρ水gV排2=G+G金属,其中V排2-V排1=S(H2-H1),由图A和图C可知,V金属=S(H3-H1),G金属=ρ金属gV金属,由上可得ρ水gV排2=ρ水gV排1+ρ金属gV金属,ρ水gS·(H2-H1)=ρ金属gS(H3-H1),则ρ金属=ρ水=×1.0×103 kg/m3=
4.0×103 kg/m3。(5)由以上计算过程可知,通过A、B、C三图就可以计算出金属块的密度,和图D操作无关,故如果图D中金属块表面沾有水,所测密度值不变。
5.(1)4 (2)无 (3)B、C
(4)错误 没有控制物体排开液体的体积相等
(5)1.1×103
解析:(1)由图可知,物体的重力为6 N,浸没在水中时弹簧测力计的示数为2 N,根据称重法测浮力可知,物体浸没在水中受到的浮力大小为F浮=G物-F示=6 N-2 N=4 N。(2)A与C、D三次实验中物体浸入液体的深度不同,根据称重法测浮力可知,C、D两次实验中弹簧测力计的示数相等,则浮力大小相等,故可以得出结论:浸没在液体中的物体所受浮力大小与其浸入液体中的深度无关。(3)验证浮力大小与物体排开液体的体积有关,则需要保持液体的密度相同,改变物体排开液体的体积,故选择A与B、 C三次实验,得出的结论是浸在液体中的物体所受浮力大小与物体排开液体的体积有关。(4)验证浮力大小与液体的密度有关,则需要保持物体排开液体的体积相等,改变液体的密度, A与B、E三次实验中液体的密度不同,物体排开液体的体积也不同,未控制单一变量,故该操作是错误的,无法得出该结论。(5)由(1)可知,物体浸没在水中时受到的浮力为4 N,则物体的体积为V=V排===4×10-4 m3,物体在盐水中所受的浮力为F浮'=G物-F示'=6 N-1.6 N=4.4 N,则步骤E中所用盐水的密度为ρ盐===1.1×103 kg/m3。
6.(1)增大 (2)A、D、E 2×103
解析:(1)根据C、 D两图可知,物体浸入液体的深度不同,但测力计的示数相同,说明浮力大小与物体浸没在液体中的深度无关;根据A、B、C三图可知,物体浸入液体的体积不同,测力计的示数不同,说明浮力大小与物体浸入液体的体积有关,物体浸入液体的体积越大,物体受到的浮力越大。(2)根据A、D、E三图可知,物体浸入液体的体积相同,但液体的密度不同,测力计的示数不同,说明浮力大小与液体的密度有关。根据图A、C可知,物体浸入水中受到的浮力F浮=G-F=4 N-2 N=2 N,根据F浮=ρ液gV排可得物体排开水的体积V排===
2×10-4 m3,因为物体浸没,所以V=V排=2×10-4 m3,根据G=mg和ρ=可得,物体的密度ρ====2×103 kg/m3。
7.(1)丁、甲、乙、丙
(2)2 1 2×103
(3)寻找普遍规律 等于
解析:(1)为了减少测量误差,可以先测量小桶的重力,再测量物体的重力,再将物体浸入水中,测出测力计对物体的拉力,最后测小桶和溢出水的总重力,所以实验顺序为丁、甲、乙、丙。(2)根据称重法测浮力可得,物体浸没在水中时受到的浮力为F浮=G-F示=F甲-F乙=4 N-2 N=2 N,根据阿基米德原理可知,物体排开水的重力为G排=F浮=2 N,所以图丁中弹簧测力计的示数应为F丁=G桶=G总-G排=3 N-2 N=1 N。物体的体积为V=V排===2×10-4 m3,由图甲可知,物体的重力为4 N,则物体的密度为ρ=====2×103 kg/m3。(3)本实验属于探究类实验,更换不同的物体和液体做实验,是为了达到多次测量寻找普遍规律的目的。由上述实验可知,浸在液体中的物体受到向上的浮力,浮力的大小等于它排开的液体所受到的重力,这就是著名的阿基米德原理。
利用浮沉条件测密度
1.用量筒测固体的密度(固体密度小于水且不吸水,水的密度用ρ水表示),方案如图所示。
① ② ③
(1)在量筒内装适量的水,读取量筒示数为V1。
(2)将固体放入量筒内,读取量筒示数为V2。
(3)用细铁丝或大头针将固体压至 于水中,读取量筒示数为V3。
(4)固体的质量m= ,固体的体积V= 。
(5)固体的密度ρ= 。
2.小明捡到一颗漂亮的小石块,他想估测出小石块的密度ρ石,回家后他利用一把刻度尺、一条细线、一个厚底薄壁圆柱形杯子(杯子厚度不计)和一桶水来测这颗小石块的密度。下面是小明测出ρ石的部分实验步骤,请你按照小明的实验思路,将实验步骤补充完整。
甲 乙
(1)将装有适量水的长杯子放入桶内的水中,使杯子 在水面上,如图甲所示,用刻度尺测出杯底到桶中水面的高度记为h1。
(2)用刻度尺测得杯底到杯内水面的高度记为h2。
(3)把小石块投入杯内水中,杯子继续竖直漂浮在水面上,如图乙所示, 。
(4) 。
(5)接着他将杯子取出,测得杯子的底面积为S。
(6)利用上述测量出的物理量和题中的已知量计算ρ石的表达式为 。
3.小桂分享他在家仅用电子秤、碗和水(已知水的密度为ρ水),测量蜡块的密度的方法:
图1 图2 图3
①如图1,用电子秤测出某圆柱体蜡块的质量为m1;
②如图2,将蜡块放入水中,静止时蜡块竖直漂浮,记下水面对应蜡块的位置;
③取出蜡块擦拭干净,并沿记号水平切下其没入水中的部分(不计损耗),称其质量为m2,如图3所示;
④结合以上测量数据算得蜡块的密度表达式为 (用m1、m2、ρ水表示)。
4.喜喜测量一金属块的密度,步骤如下:
A B C D
(1)在薄壁柱形容器中装有适量的水,将一个装有配重的薄壁厚底柱形玻璃杯放入柱形容器的水中,稳定后容器中水的深度H1=10 cm,玻璃杯露出水面的高度为h1,如图A所示。
(2)将金属块用细线吊在玻璃杯底部,稳定后容器中水的深度H2=18 cm,玻璃杯露出水面的高度为h2,如图B所示。
(3)剪断细线,稳定后容器中水的深度H3=12 cm,玻璃杯露出水面的高度为h3,如图C所示。
(4)将图C中金属块取出放入玻璃杯中,稳定后容器中水的深度为H4,玻璃杯露出水面的高度为h4,如图D所示。不计细线的体积和质量,则ρ金属= kg/m3。
(5)如果图D中金属块表面沾有水,所测金属块的密度值与真实值相比 (选填“偏大”“不变”或“偏小”)。
利用称重法和阿基米德原理测密度
5.(2024达州中考)同学们在“探究影响浮力大小的因素”实验中,根据日常生活经验提出了以下猜想:
①浮力大小与物体浸入液体中的深度有关;
②浮力大小与物体排开液体的体积有关;
③浮力大小与液体的密度有关。
实验步骤和数据如图所示:(ρ水=1.0×103 kg/m3,g取10 N/kg)
A B C D E
(1)根据实验数据,小聪计算出该物体浸没在水中受到的浮力大小是 N。
(2)为了验证猜想①,分析A与C、D三次实验,得出的结论是浸没在液体中的物体所受浮力大小与其浸入液体中的深度 (选填“有”或“无”)关。
(3)为了验证猜想②,分析A与 三次实验,得出的结论是浸在液体中的物体所受浮力大小与物体排开液体的体积有关。
(4)小聪为了验证猜想③,分析A与B、E三次实验,得出的结论是浸在液体中的物体所受浮力大小与液体的密度有关。你认为这样操作是 (选填“正确”或“错误”)的,理由是 。
(5)细心的小红利用实验数据还计算出步骤E中所用盐水的密度是 kg/m3。
6.物理兴趣小组的同学在探究影响浮力大小的因素过程中,经过讨论提出如下猜想:
猜想1:浮力的大小与物体浸入液体中的深度有关;
猜想2:浮力的大小与液体的密度有关;
猜想3:浮力的大小与物体的形状有关。
小组同学分别对以上猜想进行探究,以下是他们的实验过程。
A B C D E
(1)小凌根据A、B、C三图,认为猜想1是正确的;同组的小果根据A、C、D三图,认为猜想1是错误的。通过深入分析上述现象,小组同学一致认为浮力的大小随物体浸入液体体积的增大而 ,与物体浸没在液体中的深度无关。
(2)根据 三图,可验证猜想2是正确的。同学们通过查阅相关资料并结合图中数据,还可以测出物体的密度为 kg/m3。(ρ水=1.0×103 kg/m3,g取10 N/kg)
7.在“探究浮力的大小跟物体排开液体所受重力的关系”实验中,某同学将一个挂在弹簧测力计下的物体浸入水中进行了如图所示的实验。(ρ水=1.0×103 kg/m3,g取10 N/kg)
甲 乙 丙 丁
(1)为减少实验误差,他实验的正确顺序应为 。
(2)根据图中信息可知,物体浸没在水中时受到的浮力为 N;经计算可知,图丁中弹簧测力计的示数应为 N,物体的密度为 kg/m3。
(3)更换不同的物体和液体做实验,达到多次测量 (选填“寻找普遍规律”或“求平均值减小误差”)的目的。大量的实验结果表明,浸在液体中的物体受到向上的浮力,浮力的大小
它排开的液体所受到的重力,这就是著名的阿基米德原理。
【详解答案】
1.(3)浸没 (4)(V2-V1)ρ水 V3-V1
(5)ρ水
解析:在量筒内装适量的水,读取量筒示数为V1,将固体放入量筒内,读取量筒示数为V2,此时,固体排开水的体积为V排=V2-V1,此时,固体受到的浮力为F浮=ρ水gV排=ρ水g(V2-V1),固体处于漂浮状态,受到的浮力等于重力,即G=mg=F浮=ρ水g(V2-V1),则固体的质量为m=(V2-V1)ρ水。用细铁丝或大头针将固体压至浸没于水中,读取量筒示数为V3,此时,固体和量筒内水的总体积为V3,则固体的体积为V=V3-V1。固体的密度为ρ==ρ水。
2.(1)漂浮
(3)用刻度尺测出杯底到桶中水面的高度h3
(4)用刻度尺测出杯底到杯内水面的高度h4
(6)ρ石=
解析:(1)图甲中,将装有适量水的长杯子放入桶内的水中,使杯子漂浮在水面上。(3)把小石块投入杯内水中,杯子继续竖直漂浮在水面上,如图乙所示,小石块的重力等于杯子浮力的增加量,由G=ΔF浮=ρ水gΔV排=ρ水gS·(h3-h1)可知需要测出杯底到桶中水面的高度h3。(4)由V=S(h4-h2)可知利用排水法测量小石块体积时需要测出杯底到杯内水面的高度h4。(6)由G=mg可得,小石头的质量m=ρ水S(h3-h1),则小石头的密度ρ石===。
3. 解析:用电子秤测出某圆柱体蜡块的质量为m1,则蜡块的重力G=m1g;将蜡块放入水中,静止时蜡块竖直漂浮,则F浮=G,由阿基米德原理和浮沉条件知,ρ水gV排=m1g;解得蜡块排开水的体积:V排=,取出蜡块擦拭干净,并沿记号水平切下没入水中的部分(不计损耗),称其质量为m2,蜡块浸入水中的体积V2==V排;则有=,得蜡块的密度表达式ρ蜡=。
4.(4)4.0×103 (5)不变
解析:设容器底面积为S,玻璃杯包括配重的重力为G,由图A可知,F浮1=G,即ρ水gV排1=G,由图B可知,F浮2=G+
G金属,即ρ水gV排2=G+G金属,其中V排2-V排1=S(H2-H1),由图A和图C可知,V金属=S(H3-H1),G金属=ρ金属gV金属,由上可得ρ水gV排2=ρ水gV排1+ρ金属gV金属,ρ水gS·(H2-H1)=ρ金属gS(H3-H1),则ρ金属=ρ水=×1.0×103 kg/m3=
4.0×103 kg/m3。(5)由以上计算过程可知,通过A、B、C三图就可以计算出金属块的密度,和图D操作无关,故如果图D中金属块表面沾有水,所测密度值不变。
5.(1)4 (2)无 (3)B、C
(4)错误 没有控制物体排开液体的体积相等
(5)1.1×103
解析:(1)由图可知,物体的重力为6 N,浸没在水中时弹簧测力计的示数为2 N,根据称重法测浮力可知,物体浸没在水中受到的浮力大小为F浮=G物-F示=6 N-2 N=4 N。(2)A与C、D三次实验中物体浸入液体的深度不同,根据称重法测浮力可知,C、D两次实验中弹簧测力计的示数相等,则浮力大小相等,故可以得出结论:浸没在液体中的物体所受浮力大小与其浸入液体中的深度无关。(3)验证浮力大小与物体排开液体的体积有关,则需要保持液体的密度相同,改变物体排开液体的体积,故选择A与B、 C三次实验,得出的结论是浸在液体中的物体所受浮力大小与物体排开液体的体积有关。(4)验证浮力大小与液体的密度有关,则需要保持物体排开液体的体积相等,改变液体的密度, A与B、E三次实验中液体的密度不同,物体排开液体的体积也不同,未控制单一变量,故该操作是错误的,无法得出该结论。(5)由(1)可知,物体浸没在水中时受到的浮力为4 N,则物体的体积为V=V排===4×10-4 m3,物体在盐水中所受的浮力为F浮'=G物-F示'=6 N-1.6 N=4.4 N,则步骤E中所用盐水的密度为ρ盐===1.1×103 kg/m3。
6.(1)增大 (2)A、D、E 2×103
解析:(1)根据C、 D两图可知,物体浸入液体的深度不同,但测力计的示数相同,说明浮力大小与物体浸没在液体中的深度无关;根据A、B、C三图可知,物体浸入液体的体积不同,测力计的示数不同,说明浮力大小与物体浸入液体的体积有关,物体浸入液体的体积越大,物体受到的浮力越大。(2)根据A、D、E三图可知,物体浸入液体的体积相同,但液体的密度不同,测力计的示数不同,说明浮力大小与液体的密度有关。根据图A、C可知,物体浸入水中受到的浮力F浮=G-F=4 N-2 N=2 N,根据F浮=ρ液gV排可得物体排开水的体积V排===
2×10-4 m3,因为物体浸没,所以V=V排=2×10-4 m3,根据G=mg和ρ=可得,物体的密度ρ====2×103 kg/m3。
7.(1)丁、甲、乙、丙
(2)2 1 2×103
(3)寻找普遍规律 等于
解析:(1)为了减少测量误差,可以先测量小桶的重力,再测量物体的重力,再将物体浸入水中,测出测力计对物体的拉力,最后测小桶和溢出水的总重力,所以实验顺序为丁、甲、乙、丙。(2)根据称重法测浮力可得,物体浸没在水中时受到的浮力为F浮=G-F示=F甲-F乙=4 N-2 N=2 N,根据阿基米德原理可知,物体排开水的重力为G排=F浮=2 N,所以图丁中弹簧测力计的示数应为F丁=G桶=G总-G排=3 N-2 N=1 N。物体的体积为V=V排===2×10-4 m3,由图甲可知,物体的重力为4 N,则物体的密度为ρ=====2×103 kg/m3。(3)本实验属于探究类实验,更换不同的物体和液体做实验,是为了达到多次测量寻找普遍规律的目的。由上述实验可知,浸在液体中的物体受到向上的浮力,浮力的大小等于它排开的液体所受到的重力,这就是著名的阿基米德原理。
