6.2向心力(共23张PPT)物理人教版(2019)必修第二册
文档属性
| 名称 | 6.2向心力(共23张PPT)物理人教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-16 10:26:03 | ||
图片预览








文档简介
(共23张PPT)
6.2 向心力
学习目标
1.知道什么是向心力,知道向心力的作用,知道它是根据力的作用效果命名的.
2.会分析向心力的来源,掌握向心力的表达式,并能用来进行计算.
3.体验向心力的存在,会设计相关实验,探究向心力与物体的质量、速度和轨道半径的关系,体会控制变量法在研究多个物理量关系中的应用.
4.知道变速圆周运动和一般曲线运动的受力特点.
这就是我们今天将要学习的问题。
空中飞椅与人一起做匀速圆周运动。
你知道它们在运动过程中所受合力的方向有什么特点吗?
情景引入
一个小球在细线的牵引下,绕光滑桌面上的图钉做匀速圆周运动。用剪刀将细线剪断,观察小球将做什么运动?你认为使小球做圆周运动的力指向何方?
思考与讨论
一、向心力
下面我们从受力分析开始分析
新知讲解
O
G
FN
F
O
FN与G相平衡,所以合力为拉力F
用剪刀将细线剪断,小球将沿切线方向飞出,做匀速直线运动。
结论:对于做匀速圆周运动的小球
1、所受的合力为细线的拉力;
2、拉力即为使小球做圆周运动的力;
3、拉力的方向指向圆心。
向心力
1.定义:做匀速圆周运动的物体所受的合力总指向 ,这个指向 的 力叫作向心力.
2.方向:始终沿着 指向 .
3.作用:只改变速度的 ,不改变速度的 .
4.向心力的来源:向心力是由 提供的.是根据力
的 命名的,
圆心
圆心
半径
圆心
方向
大小
作用效果
某个力或者几个力的合力
自学感知 梳理教材夯实基础
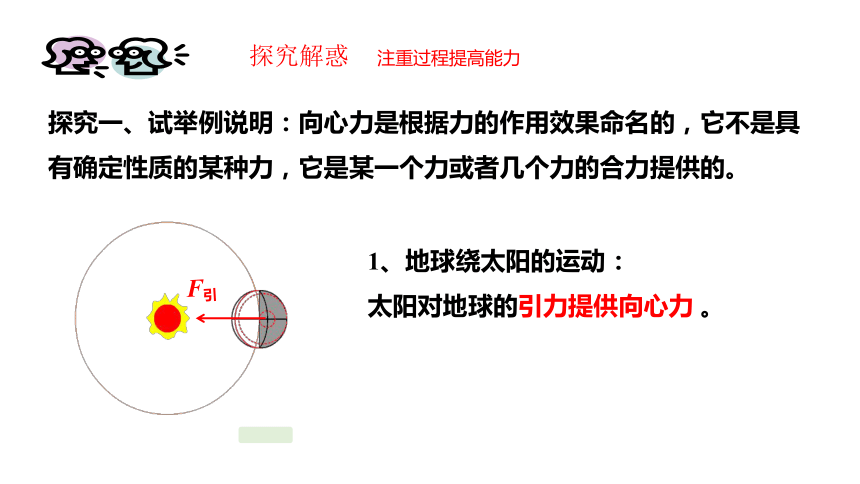
1、地球绕太阳的运动:
太阳对地球的引力提供向心力 。
F引
探究一、试举例说明:向心力是根据力的作用效果命名的,它不是具有确定性质的某种力,它是某一个力或者几个力的合力提供的。
探究解惑 注重过程提高能力
O'
ω
O
θ
l
m
mg
F合
FT
2、飞椅与人一起做圆周运动:
向心力 F合 则是由绳子斜向上方的拉力 F T和所受重力 mg 的合力提供的。
二、向心力的大小
因此,我们可以先通过实验感受向心力大小与圆周运动的一些运动学量之间的定性关系,再通过实验,进一步探究向心力的大小与这些量的定量关系。
新知讲解
认识物理量的方法:先定性了解,再探究定量关系
操作步骤:
1、在绳子的一端拴一个小沙袋,另一端握在手中,将手举过头顶, 使沙袋在水平面内做圆周运动。沙袋所受的向心力近似等于手通过绳对沙袋的拉力。
感受向心力(定性了解)
(一)、做一做
r
2、设沙袋转动的速度为V,绳的长度为L,沙袋的质量为m
(1)保持V和L不变,改变m,感受向心力的变化。
(3)保持m和V不变,改变L,感受向心力的变化。
(2)保持L和m不变,改变V,感受向心力的变化。
3、结论:向心力的大小与物体的质量、速度、轨道半径等因素有关系。
探究向心力大小的表达式(定量关系)
1、实验器材:向心力演示器、两个质量相同的钢球和一个质量小的铝球。
向心力演示器
1
2
4
3
5
8
7
6
2、向心力演示器的构造及工作原理:
匀速转动手柄 1、可以使变速塔轮 2 和 3 以及长槽 4 和短槽 5随之匀速转动,横臂 6的挡板对小球的压力提供向心力,该力的反作用力通过弹簧测力套筒 7的下降和标尺 8上露出的等分标记,可以粗略的计算出两个小球所受向心力的比值。
(二)、实验
①控制小球质量和半径不变,探究向心力与__________的关系。
②控制小球质量和角速度不变,探究向心力与________的关系。
③控制小球半径和角速度不变,探究向心力与________的关系。
角速度
半径
质量
3.实验原理
探究方法:控制变量法。
4、实验步骤
(1)把两个质量相同的小球放在长槽和短槽上,使它们的转动半径相同。调整塔轮上的皮带,使两个小球的角速度不一样。注意向心力的大小与角速度的关系。
(3)换成质量不同的小球,分别使两小球的转动半径相同。调整塔轮上的皮带,使两个小球的角速度也相同。注意向心力的大小与质量的关系。
(4)重复几次以上实验。
(2)保持两个小球质量不变,增大长槽上小球的转动半径。调整塔轮上的皮带,使两个小球的角速度相同。注意向心力的大小与半径的关系。
实验演示
5、数据收集与分析
(1).m、r一定
(2).m、ω一定
序号 1 2 3 4 5 6
F向
r
序号 1 2 3 4 5 6
F向
ω
ω2
序号 1 2 3 4 5 6
F向
r
(3).r、ω一定
(4).分别作出F向-ω2、F向-r、F向-m的图像。
6.实验结论:
(1)在质量和半径一定的情况下,向心力的大小与角速度的平方成正比。
(2)在质量和角速度一定的情况下,向心力的大小与半径成正比。
(3)在半径和角速度一定的情况下,向心力的大小与质量成正比。
精确的实验表明,向心力的大小可以表示为:Fn = mω2r
或
v2
Fn=m——
r
(1)确定研究对象、轨迹圆周(含圆心、半径和轨道平面).
(2)受力分析(画图),写出指向圆心的合力的表达式(合成法、正交分解法等).
(3)根据合力等于向心力列方程,必要时列出其他相关方程.
(4)统一单位,代入数据计算,求出结果或进行讨论.
注意:第(1)步是关键;第(2)步是难点;第(3)步是重点。
探究解惑 注重过程提高能力
探究二、解答匀速圆周运动问题的一般步骤:
例题1.如图所示,沿半径为R的半球型碗的光滑内表面,质量为m的小球正在虚线所示的水平面内做匀速圆周运动,小球离碗底的高度h= ,试求(结果可用根号表示):
(1)此时小球对碗壁的压力大小。
(2)小球做匀速圆周运动的线速度大小。
(3)小球做匀速圆周运动的周期大小。
【解析】(1)由几何关系可知,支持力与水平方向的夹角为:θ=30°
对小球受力分析可知:FNsin 30°= mg,
解得:FN= 2 mg。
(2)根据牛顿第二定律可知:FNcos 30°=
解得:v= 。
(3)根据T= 可得:T=
根据 F产生的效果,可以把 F 分解为两个相互垂直的分力:跟圆周相切的分力 Ft 和指向圆心的分力 Fn。Ft 与沙袋运动的速度同向,使得沙袋的速度越来越大 ;Fn 指向圆心,提供沙袋做圆周运动所需的向心力,改变沙袋速度的方向。
F
Fn
Ft
Fn 改变速度的方向 Ft改变速度的大小
v0
如图:我们使沙袋加速转动时,绳子牵引沙袋的方向并不严格指向圆心。O是沙袋运动轨迹的圆心,F 是绳对沙袋的拉力
1、变速圆周运动的特点
三、变速圆周运动和一般曲线运动的受力特点
F
O
新知讲解
r2
r1
2、一般的曲线运动
(1)定义:运动轨迹既不是直线也不是圆周的曲线运动,可以称为一般的曲线运动。
(2)研究方法:采用圆周运动的分析方法来处理
在研究时,可以把这条曲线分割为许多很短的小段,质点在每小段的运动都可以看作圆周运动的一部分。
v
v
(1)合外力方向与速度方向夹角为锐角时,力为动力,速率越来越大.
(2)合外力方向与速度方向夹角为钝角时,力为阻力,速率越来越小.
探究3、怎样根据合力的方向特点判断一般曲线运动的速率变化?
Ft 与物体运动的速度反向,使得物体的速度越来越小 ;Fn 指向圆心,提供物体做圆周运动所需的向心力,改变物体速度的方向。
F
Fn
Ft
v0
例题2、如图所示,在物体沿曲线从M点到N点的运动过程中,速度逐渐减小.在此过程中物体所受合力F的方向可能是
√
解析 做曲线运动的物体所受合力的方向总是指向曲线凹侧,A、D错误;由于速度逐渐减小,故合力F的方向与速度方向的夹角应大于90°,C正确,B错误.
课堂小结
1、做匀速圆周运动的物体所受的合力总指向圆心,这个指向圆心的力就叫作向心力,用符号:Fn
2、方向:始终指向圆心(与v 垂直或与半径垂直),是变力。
3、向心力来源
向心力是根据力的作用效果命名的,它不是具有确定性质的某种力,它可以是某一个力或者几个力的合力提供的。
4、向心力的大小可以表示为:Fn = mω2r Fn= mv2/r
6.2 向心力
学习目标
1.知道什么是向心力,知道向心力的作用,知道它是根据力的作用效果命名的.
2.会分析向心力的来源,掌握向心力的表达式,并能用来进行计算.
3.体验向心力的存在,会设计相关实验,探究向心力与物体的质量、速度和轨道半径的关系,体会控制变量法在研究多个物理量关系中的应用.
4.知道变速圆周运动和一般曲线运动的受力特点.
这就是我们今天将要学习的问题。
空中飞椅与人一起做匀速圆周运动。
你知道它们在运动过程中所受合力的方向有什么特点吗?
情景引入
一个小球在细线的牵引下,绕光滑桌面上的图钉做匀速圆周运动。用剪刀将细线剪断,观察小球将做什么运动?你认为使小球做圆周运动的力指向何方?
思考与讨论
一、向心力
下面我们从受力分析开始分析
新知讲解
O
G
FN
F
O
FN与G相平衡,所以合力为拉力F
用剪刀将细线剪断,小球将沿切线方向飞出,做匀速直线运动。
结论:对于做匀速圆周运动的小球
1、所受的合力为细线的拉力;
2、拉力即为使小球做圆周运动的力;
3、拉力的方向指向圆心。
向心力
1.定义:做匀速圆周运动的物体所受的合力总指向 ,这个指向 的 力叫作向心力.
2.方向:始终沿着 指向 .
3.作用:只改变速度的 ,不改变速度的 .
4.向心力的来源:向心力是由 提供的.是根据力
的 命名的,
圆心
圆心
半径
圆心
方向
大小
作用效果
某个力或者几个力的合力
自学感知 梳理教材夯实基础
1、地球绕太阳的运动:
太阳对地球的引力提供向心力 。
F引
探究一、试举例说明:向心力是根据力的作用效果命名的,它不是具有确定性质的某种力,它是某一个力或者几个力的合力提供的。
探究解惑 注重过程提高能力
O'
ω
O
θ
l
m
mg
F合
FT
2、飞椅与人一起做圆周运动:
向心力 F合 则是由绳子斜向上方的拉力 F T和所受重力 mg 的合力提供的。
二、向心力的大小
因此,我们可以先通过实验感受向心力大小与圆周运动的一些运动学量之间的定性关系,再通过实验,进一步探究向心力的大小与这些量的定量关系。
新知讲解
认识物理量的方法:先定性了解,再探究定量关系
操作步骤:
1、在绳子的一端拴一个小沙袋,另一端握在手中,将手举过头顶, 使沙袋在水平面内做圆周运动。沙袋所受的向心力近似等于手通过绳对沙袋的拉力。
感受向心力(定性了解)
(一)、做一做
r
2、设沙袋转动的速度为V,绳的长度为L,沙袋的质量为m
(1)保持V和L不变,改变m,感受向心力的变化。
(3)保持m和V不变,改变L,感受向心力的变化。
(2)保持L和m不变,改变V,感受向心力的变化。
3、结论:向心力的大小与物体的质量、速度、轨道半径等因素有关系。
探究向心力大小的表达式(定量关系)
1、实验器材:向心力演示器、两个质量相同的钢球和一个质量小的铝球。
向心力演示器
1
2
4
3
5
8
7
6
2、向心力演示器的构造及工作原理:
匀速转动手柄 1、可以使变速塔轮 2 和 3 以及长槽 4 和短槽 5随之匀速转动,横臂 6的挡板对小球的压力提供向心力,该力的反作用力通过弹簧测力套筒 7的下降和标尺 8上露出的等分标记,可以粗略的计算出两个小球所受向心力的比值。
(二)、实验
①控制小球质量和半径不变,探究向心力与__________的关系。
②控制小球质量和角速度不变,探究向心力与________的关系。
③控制小球半径和角速度不变,探究向心力与________的关系。
角速度
半径
质量
3.实验原理
探究方法:控制变量法。
4、实验步骤
(1)把两个质量相同的小球放在长槽和短槽上,使它们的转动半径相同。调整塔轮上的皮带,使两个小球的角速度不一样。注意向心力的大小与角速度的关系。
(3)换成质量不同的小球,分别使两小球的转动半径相同。调整塔轮上的皮带,使两个小球的角速度也相同。注意向心力的大小与质量的关系。
(4)重复几次以上实验。
(2)保持两个小球质量不变,增大长槽上小球的转动半径。调整塔轮上的皮带,使两个小球的角速度相同。注意向心力的大小与半径的关系。
实验演示
5、数据收集与分析
(1).m、r一定
(2).m、ω一定
序号 1 2 3 4 5 6
F向
r
序号 1 2 3 4 5 6
F向
ω
ω2
序号 1 2 3 4 5 6
F向
r
(3).r、ω一定
(4).分别作出F向-ω2、F向-r、F向-m的图像。
6.实验结论:
(1)在质量和半径一定的情况下,向心力的大小与角速度的平方成正比。
(2)在质量和角速度一定的情况下,向心力的大小与半径成正比。
(3)在半径和角速度一定的情况下,向心力的大小与质量成正比。
精确的实验表明,向心力的大小可以表示为:Fn = mω2r
或
v2
Fn=m——
r
(1)确定研究对象、轨迹圆周(含圆心、半径和轨道平面).
(2)受力分析(画图),写出指向圆心的合力的表达式(合成法、正交分解法等).
(3)根据合力等于向心力列方程,必要时列出其他相关方程.
(4)统一单位,代入数据计算,求出结果或进行讨论.
注意:第(1)步是关键;第(2)步是难点;第(3)步是重点。
探究解惑 注重过程提高能力
探究二、解答匀速圆周运动问题的一般步骤:
例题1.如图所示,沿半径为R的半球型碗的光滑内表面,质量为m的小球正在虚线所示的水平面内做匀速圆周运动,小球离碗底的高度h= ,试求(结果可用根号表示):
(1)此时小球对碗壁的压力大小。
(2)小球做匀速圆周运动的线速度大小。
(3)小球做匀速圆周运动的周期大小。
【解析】(1)由几何关系可知,支持力与水平方向的夹角为:θ=30°
对小球受力分析可知:FNsin 30°= mg,
解得:FN= 2 mg。
(2)根据牛顿第二定律可知:FNcos 30°=
解得:v= 。
(3)根据T= 可得:T=
根据 F产生的效果,可以把 F 分解为两个相互垂直的分力:跟圆周相切的分力 Ft 和指向圆心的分力 Fn。Ft 与沙袋运动的速度同向,使得沙袋的速度越来越大 ;Fn 指向圆心,提供沙袋做圆周运动所需的向心力,改变沙袋速度的方向。
F
Fn
Ft
Fn 改变速度的方向 Ft改变速度的大小
v0
如图:我们使沙袋加速转动时,绳子牵引沙袋的方向并不严格指向圆心。O是沙袋运动轨迹的圆心,F 是绳对沙袋的拉力
1、变速圆周运动的特点
三、变速圆周运动和一般曲线运动的受力特点
F
O
新知讲解
r2
r1
2、一般的曲线运动
(1)定义:运动轨迹既不是直线也不是圆周的曲线运动,可以称为一般的曲线运动。
(2)研究方法:采用圆周运动的分析方法来处理
在研究时,可以把这条曲线分割为许多很短的小段,质点在每小段的运动都可以看作圆周运动的一部分。
v
v
(1)合外力方向与速度方向夹角为锐角时,力为动力,速率越来越大.
(2)合外力方向与速度方向夹角为钝角时,力为阻力,速率越来越小.
探究3、怎样根据合力的方向特点判断一般曲线运动的速率变化?
Ft 与物体运动的速度反向,使得物体的速度越来越小 ;Fn 指向圆心,提供物体做圆周运动所需的向心力,改变物体速度的方向。
F
Fn
Ft
v0
例题2、如图所示,在物体沿曲线从M点到N点的运动过程中,速度逐渐减小.在此过程中物体所受合力F的方向可能是
√
解析 做曲线运动的物体所受合力的方向总是指向曲线凹侧,A、D错误;由于速度逐渐减小,故合力F的方向与速度方向的夹角应大于90°,C正确,B错误.
课堂小结
1、做匀速圆周运动的物体所受的合力总指向圆心,这个指向圆心的力就叫作向心力,用符号:Fn
2、方向:始终指向圆心(与v 垂直或与半径垂直),是变力。
3、向心力来源
向心力是根据力的作用效果命名的,它不是具有确定性质的某种力,它可以是某一个力或者几个力的合力提供的。
4、向心力的大小可以表示为:Fn = mω2r Fn= mv2/r
