人教A版《高中数学》选择性必修第三册7.1.2全概率公式 课件(共21张PPT)
文档属性
| 名称 | 人教A版《高中数学》选择性必修第三册7.1.2全概率公式 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-18 08:49:45 | ||
图片预览






文档简介
(共21张PPT)
人教A版《高中数学》选择性必修第三册第七章第二节
7.1.2全概率公式
复习旧知
例3 银行储蓄卡的密码由 6位数字组成. 某人在银行自助取款机上取钱时,忘记了密码的最后1位数字. 求:
(1) 任意按最后1位数字,不超过2次就按对的概率;
(1) 设Ai=“第i次按对密码”(i=1, 2),则事件“不超过2次就按对密码”可表示为
古希腊有一个聪明的囚徒被国王判了死刑,国王听说他很聪明,就给了他一次免死的机会。
国王:“现在有两个坛子,50个白球和50个黑球,你可以随意的把这100个球混合后放到两个坛子中,然后蒙上眼睛,任取一坛,再任摸一球,如果摸到白球能免你一死。”
创设情境
囚徒的智慧
囚徒:“怎么办呢?如何分配这100个球,才能够使我死里逃生的机会更大呢?”
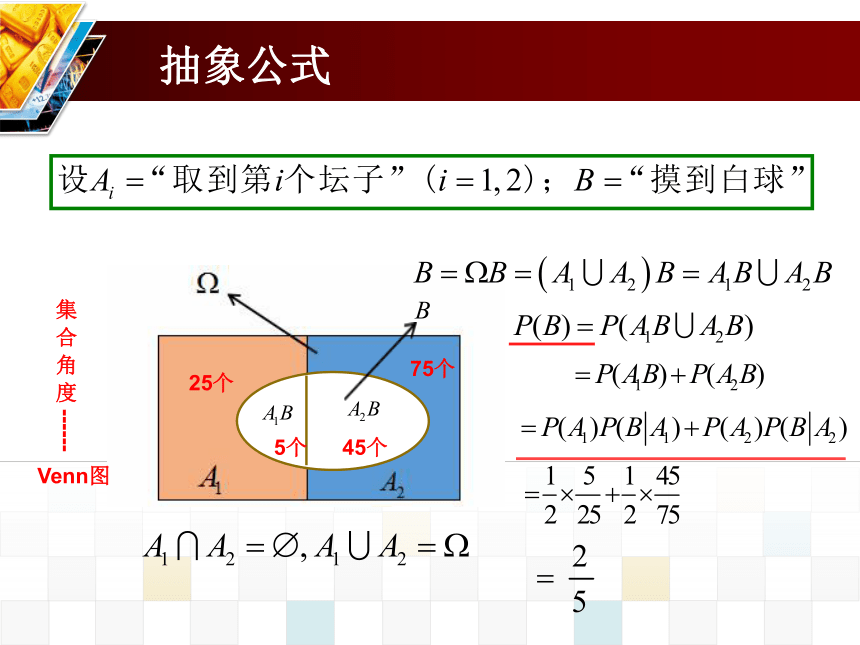
抽象公式
囚徒的智慧
囚徒:假设将5个白球和20个黑球放到1号坛子里,剩下的45个白球和30个黑球放到2号坛子里,现在从两个坛子中任取一坛,再从中任摸一球,求摸到白球的概率是多少?也就是能够死里逃生的机会有多大呢?
5个
20个
45个
30个
1号 2号
抽象公式
抽象公式
集 合 角 度 ------
5个
25个
45个
75个
Venn图
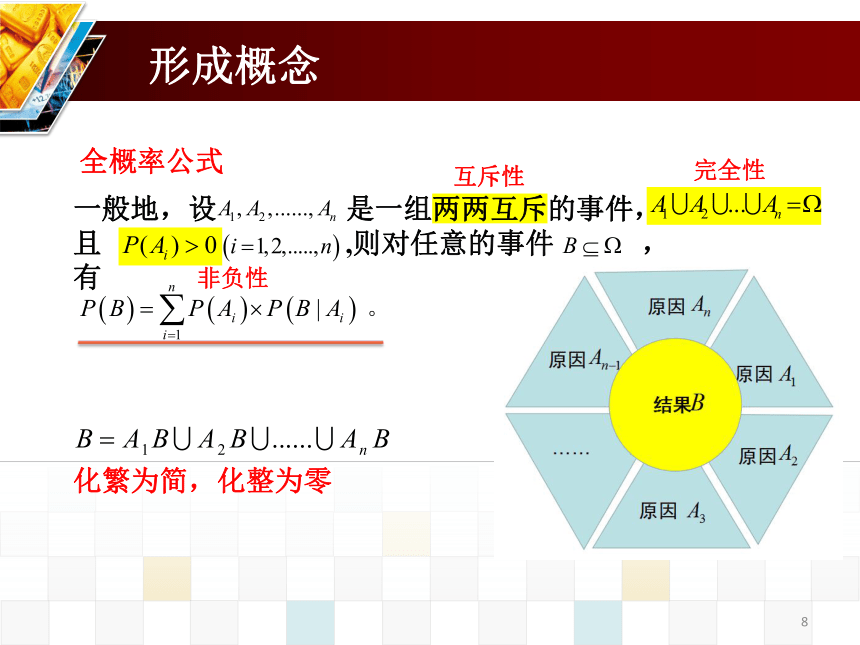
五、教学过程A1A2A3An..........AnBA3BBA2BA1B 合作探究探究一如果第一步实验的结果有n个,则对任意的事件全概率公式一般地,设是一组两两互斥的事件,且,则对任意的事件,有化繁为简,化整为零五、教学过程形成概念互斥性完全性非负性形成概念
公式运用
路径角度
解:
试一试:假设将5个白球和20个黑球放到1号坛子里,剩下的45个白球和30个黑球放到2号坛子里,现在从两个坛子中任取一坛,再从中任摸一球,求摸到白球的概率是多少?也就是能够死里逃生的机会有多大呢?
——概率树图
1.设事件
2.找划分
3.写概率
4.代公式
公式运用
路径角度
解:
试一试:假设将5个白球和20个黑球放到1号坛子里,剩下的45个白球和30个黑球放到2号坛子里,现在从两个坛子中任取一坛,再从中任摸一球,求摸到白球的概率是多少?也就是能够死里逃生的机会有多大呢?
——概率树图
1.设事件
2.找划分
3.写概率
4.代公式
互斥事件
条件概率
原因
由因导果
结果
....
....
....
探究二
在刚才的方案中,我们计算出了囚徒“死里逃生”的概率为0.4,请同学们思考,是否有更好的方案呢?
公式运用
扬长
补短
公式运用
例:有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.己知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
运用公式
例:有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.己知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
运用公式
(2)如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
合作探究
1.本题中的实际意义是什么?
探究三
2.解决问题(2)的关键等式是什么?
贝叶斯公式一般地,设是一组两两互斥的事件,且,则对任意的事件,,有五、教学过程公式拓展该公式由英国数学家贝叶斯(Bayes)给出.它是在观察到事件B已发生的条件下,寻找导致B发生的每个原因的概率.对分子用乘法公式分母用全概率公式医学应用
X光片的病理诊断案例
一、教材分析实际问题条件概率加法公式乘法公式全概率公式抽象贝叶斯公式统计分析信用估计质量检验风险分析病例诊断......执果索因由因求果大单元目标检测
A.第二天去甲影院的概率为0.54
B.第二天去乙影院的概率为0.44
D.第二天去了甲影院,则第一天去乙影院的概率为
C.第二天去了乙影院,则第一天去甲影院的概率为
AC
本节课你有哪些收获
公式巩固
公式拓展
——数学抽象
逻辑推理
——数学运算
数据分析
公式生成
数学核心素养
本节思路
问题解决
生活无处不数学,
爱生活,爱数学,
共筑美好未来!
问题提出
总结提升
到生活中去
从生活中来
——
人教A版《高中数学》选择性必修第三册第七章第二节
7.1.2全概率公式
复习旧知
例3 银行储蓄卡的密码由 6位数字组成. 某人在银行自助取款机上取钱时,忘记了密码的最后1位数字. 求:
(1) 任意按最后1位数字,不超过2次就按对的概率;
(1) 设Ai=“第i次按对密码”(i=1, 2),则事件“不超过2次就按对密码”可表示为
古希腊有一个聪明的囚徒被国王判了死刑,国王听说他很聪明,就给了他一次免死的机会。
国王:“现在有两个坛子,50个白球和50个黑球,你可以随意的把这100个球混合后放到两个坛子中,然后蒙上眼睛,任取一坛,再任摸一球,如果摸到白球能免你一死。”
创设情境
囚徒的智慧
囚徒:“怎么办呢?如何分配这100个球,才能够使我死里逃生的机会更大呢?”
抽象公式
囚徒的智慧
囚徒:假设将5个白球和20个黑球放到1号坛子里,剩下的45个白球和30个黑球放到2号坛子里,现在从两个坛子中任取一坛,再从中任摸一球,求摸到白球的概率是多少?也就是能够死里逃生的机会有多大呢?
5个
20个
45个
30个
1号 2号
抽象公式
抽象公式
集 合 角 度 ------
5个
25个
45个
75个
Venn图
五、教学过程A1A2A3An..........AnBA3BBA2BA1B 合作探究探究一如果第一步实验的结果有n个,则对任意的事件全概率公式一般地,设是一组两两互斥的事件,且,则对任意的事件,有化繁为简,化整为零五、教学过程形成概念互斥性完全性非负性形成概念
公式运用
路径角度
解:
试一试:假设将5个白球和20个黑球放到1号坛子里,剩下的45个白球和30个黑球放到2号坛子里,现在从两个坛子中任取一坛,再从中任摸一球,求摸到白球的概率是多少?也就是能够死里逃生的机会有多大呢?
——概率树图
1.设事件
2.找划分
3.写概率
4.代公式
公式运用
路径角度
解:
试一试:假设将5个白球和20个黑球放到1号坛子里,剩下的45个白球和30个黑球放到2号坛子里,现在从两个坛子中任取一坛,再从中任摸一球,求摸到白球的概率是多少?也就是能够死里逃生的机会有多大呢?
——概率树图
1.设事件
2.找划分
3.写概率
4.代公式
互斥事件
条件概率
原因
由因导果
结果
....
....
....
探究二
在刚才的方案中,我们计算出了囚徒“死里逃生”的概率为0.4,请同学们思考,是否有更好的方案呢?
公式运用
扬长
补短
公式运用
例:有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.己知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
运用公式
例:有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.己知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
运用公式
(2)如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
合作探究
1.本题中的实际意义是什么?
探究三
2.解决问题(2)的关键等式是什么?
贝叶斯公式一般地,设是一组两两互斥的事件,且,则对任意的事件,,有五、教学过程公式拓展该公式由英国数学家贝叶斯(Bayes)给出.它是在观察到事件B已发生的条件下,寻找导致B发生的每个原因的概率.对分子用乘法公式分母用全概率公式医学应用
X光片的病理诊断案例
一、教材分析实际问题条件概率加法公式乘法公式全概率公式抽象贝叶斯公式统计分析信用估计质量检验风险分析病例诊断......执果索因由因求果大单元目标检测
A.第二天去甲影院的概率为0.54
B.第二天去乙影院的概率为0.44
D.第二天去了甲影院,则第一天去乙影院的概率为
C.第二天去了乙影院,则第一天去甲影院的概率为
AC
本节课你有哪些收获
公式巩固
公式拓展
——数学抽象
逻辑推理
——数学运算
数据分析
公式生成
数学核心素养
本节思路
问题解决
生活无处不数学,
爱生活,爱数学,
共筑美好未来!
问题提出
总结提升
到生活中去
从生活中来
——
