人教B版必修三 数学建模活动:周期现象的描述 课件(共25张PPT)
文档属性
| 名称 | 人教B版必修三 数学建模活动:周期现象的描述 课件(共25张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-18 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
4.2.1数学建模活动:周期现象的描述
学习 目标 1.了解三角函数是描述周期变化现象的重要函数模型,并会用三角函数模型解决一些简单的实际问题。(重点)
2.实际问题抽象为三角函数模型,培养数学应用意识。(重点、难点)
3.提高利用信息技术处理一些实际计算的能力。(难点)
核心 素养 1.通过建立三角模型解决实际问题,培养数学建模素养。
2.借助实际问题求解,提升数学运算素养。
若干年后,如果在座的各位同学有机会当上船长,当你的船只要到某个港口去 ,你作为船长,你希望知道那个港口的一些什么情况?
创设情境、提出问题
在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋。下面是某港口在某季节每天的时间与水深(单位:m)记录表。
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 5.0
问题1:观察表格中的数据,你能够从中得到一些什么信息?
问题2:如何更加直观地看出这种周期性变化规律?
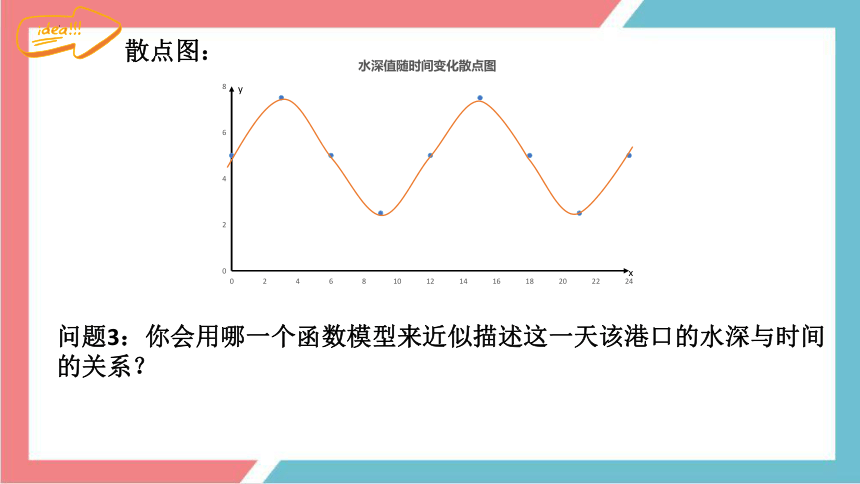
散点图:
y
x
问题3:你会用哪一个函数模型来近似描述这一天该港口的水深与时间的关系?
分析问题、建立模型
小组合作探究1:
问题4:怎样求出三角函数模型?并给出一天24小时内整点水深值数值表。
x
小组合作探究1:
问题4:怎样求出三角函数模型?并给出一天24小时内整点水深值数值表。
x
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
00
01
:
开始/重置
00
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
02
03
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
04
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
05
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
06
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
小组合作探究1:
问题4:怎样求出三角函数模型?并给出一天24小时内整点水深值数值表。
x
ggb1
时刻 0 1 2 3 4 5 6 7 8 9 10 11 12
水深 5.000 6.250 7.165 7.500 7.165 6.250 5.000 3.754 2.835 2.500 2.835 3.754 5.000
时刻 13 14 15 16 17 18 19 20 21 22 23 24
水深 6.250 7.165 7.500 7.165 6.250 5.000 3.754 2.835 2.500 2.835 3.754 5.000
24小时内整点水深值数值表
有了水深关于时间的函数模型以后,作为船长考虑的问题还没有结束,因为船只在进出港时,每艘船只的吃水深度是不一样,下面我们就看一看把这两方面的情况都考虑进去的一个问题:
验证模型、应用模型
问题5:一艘货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能呆多久?
小组合作探究2:
用数学的眼光看,这里研究的是一个怎样的数学问题?
如何解决?
问题5:一艘货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能呆多久?
小组合作探究2:
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
00
01
:
开始/重置
00
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
02
03
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
04
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
05
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
问题5:一艘货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能呆多久?
小组合作探究2:
分析:水深,即
ggb2
转化为时刻:
A点00:23,B点5:37,C点12:37,D点17:37
该船在00:23至5:37或12:23至17:37安全进港
若当天安全离港,最多停留5h14min.
刚才整个过程,货船在进港,在港口停留,到后来离开港口,货船的吃深深度一直没有改变,也就是说货船的安全深度一直没有改变,但是实际情况往往是货船载满货物进港,在港口卸货,在卸货的过程中,由物理学的知识我们知道,随着船身自身重量的减小,船身会上浮,这样一来当两者都在改变的时候,我们又该如何选择进出港时间呢?请看下面问题:
问题6:在探究2条件中,若该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?
小组合作探究3:
问题6:在探究2条件中,若该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?
小组合作探究3:
安全即需要:实际水深 安全水深,
即
ggb3
转化为时刻:
F点6:43
该船在6:43必须停止卸货,将船驶向较深水域.
课堂小结
本节课你有什么收获?
知识:
数学思想与方法:
启发:
数学建模求解实际问题过程
三角函数模型
应用Ggb软件
转化
数形结合
类比
数学与生活息息相关
探究实际问题的范例
课后作业
(1)针对本节课所学内容完成研究报告;
(2)了解更多生活中与三角函数模型有关的现象;
(3)一个城市所在的经度和纬度是如何影响日出和日落的时间的?收集有关数据,并提供理论证据支持你的结论。
数学是知识的工具,亦是其它知识工具的源泉。所有研究顺序和度量的科学均和数学有关。
——笛卡尔
4.2.1数学建模活动:周期现象的描述
学习 目标 1.了解三角函数是描述周期变化现象的重要函数模型,并会用三角函数模型解决一些简单的实际问题。(重点)
2.实际问题抽象为三角函数模型,培养数学应用意识。(重点、难点)
3.提高利用信息技术处理一些实际计算的能力。(难点)
核心 素养 1.通过建立三角模型解决实际问题,培养数学建模素养。
2.借助实际问题求解,提升数学运算素养。
若干年后,如果在座的各位同学有机会当上船长,当你的船只要到某个港口去 ,你作为船长,你希望知道那个港口的一些什么情况?
创设情境、提出问题
在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋。下面是某港口在某季节每天的时间与水深(单位:m)记录表。
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 5.0
问题1:观察表格中的数据,你能够从中得到一些什么信息?
问题2:如何更加直观地看出这种周期性变化规律?
散点图:
y
x
问题3:你会用哪一个函数模型来近似描述这一天该港口的水深与时间的关系?
分析问题、建立模型
小组合作探究1:
问题4:怎样求出三角函数模型?并给出一天24小时内整点水深值数值表。
x
小组合作探究1:
问题4:怎样求出三角函数模型?并给出一天24小时内整点水深值数值表。
x
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
00
01
:
开始/重置
00
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
02
03
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
04
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
05
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
06
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
小组合作探究1:
问题4:怎样求出三角函数模型?并给出一天24小时内整点水深值数值表。
x
ggb1
时刻 0 1 2 3 4 5 6 7 8 9 10 11 12
水深 5.000 6.250 7.165 7.500 7.165 6.250 5.000 3.754 2.835 2.500 2.835 3.754 5.000
时刻 13 14 15 16 17 18 19 20 21 22 23 24
水深 6.250 7.165 7.500 7.165 6.250 5.000 3.754 2.835 2.500 2.835 3.754 5.000
24小时内整点水深值数值表
有了水深关于时间的函数模型以后,作为船长考虑的问题还没有结束,因为船只在进出港时,每艘船只的吃水深度是不一样,下面我们就看一看把这两方面的情况都考虑进去的一个问题:
验证模型、应用模型
问题5:一艘货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能呆多久?
小组合作探究2:
用数学的眼光看,这里研究的是一个怎样的数学问题?
如何解决?
问题5:一艘货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能呆多久?
小组合作探究2:
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
00
01
:
开始/重置
00
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
02
03
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
04
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
05
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
09
08
07
06
05
04
03
02
01
00
问题5:一艘货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能呆多久?
小组合作探究2:
分析:水深,即
ggb2
转化为时刻:
A点00:23,B点5:37,C点12:37,D点17:37
该船在00:23至5:37或12:23至17:37安全进港
若当天安全离港,最多停留5h14min.
刚才整个过程,货船在进港,在港口停留,到后来离开港口,货船的吃深深度一直没有改变,也就是说货船的安全深度一直没有改变,但是实际情况往往是货船载满货物进港,在港口卸货,在卸货的过程中,由物理学的知识我们知道,随着船身自身重量的减小,船身会上浮,这样一来当两者都在改变的时候,我们又该如何选择进出港时间呢?请看下面问题:
问题6:在探究2条件中,若该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?
小组合作探究3:
问题6:在探究2条件中,若该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?
小组合作探究3:
安全即需要:实际水深 安全水深,
即
ggb3
转化为时刻:
F点6:43
该船在6:43必须停止卸货,将船驶向较深水域.
课堂小结
本节课你有什么收获?
知识:
数学思想与方法:
启发:
数学建模求解实际问题过程
三角函数模型
应用Ggb软件
转化
数形结合
类比
数学与生活息息相关
探究实际问题的范例
课后作业
(1)针对本节课所学内容完成研究报告;
(2)了解更多生活中与三角函数模型有关的现象;
(3)一个城市所在的经度和纬度是如何影响日出和日落的时间的?收集有关数据,并提供理论证据支持你的结论。
数学是知识的工具,亦是其它知识工具的源泉。所有研究顺序和度量的科学均和数学有关。
——笛卡尔
