人教版六年级下册数学第四单元 正比例和反比例复习课 课件(共18张PPT)
文档属性
| 名称 | 人教版六年级下册数学第四单元 正比例和反比例复习课 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 08:24:20 | ||
图片预览






文档简介
(共18张PPT)
正比例和反比例
(复习课)
人教版小学数学六年级下册第四单元
单位:XXXX
授课人:XXX
课前计算训练营
1.填一填。
4×6=60×( ) 2.4×( )=2×12 36×( )= 1.8×6
3650dm =( )m 1.75时=( )分钟 公顷=( )m
( ):8=0.625=30:( ) = =( )%
24
( )
2.算一算。
2019×0.125×8= 72÷ = 7× ÷7× =
1.5×101-1.5= 6 -3 = 25×4%=
0.87+0.3= 1÷25%= 3.14×90=
0.4
10
0.3
3.65
105
1250
5
48
15
62.5
2019
32
150
9
1
1.17
4
282.6
1
通过复习,进一步认识正比例和反比例的意义,了解正、反比例的联系与区别,能正确判断正、反比例;
2
3
学习目标
通过回顾梳理,感悟知识之间的联系,建构正比例、反比例相关的知识网络;
发展分析、比较、抽象、概括的能力,激发探索数学知识和规律的兴趣。
1.结合思维导图,小组内分享关于正比例和反比例的有关知识;
2.叙述各自绘图思路,讨论并总结该部分知识的框架和具体体系;
3.推选代表,展示发言。
一、回顾梳理,集中展示
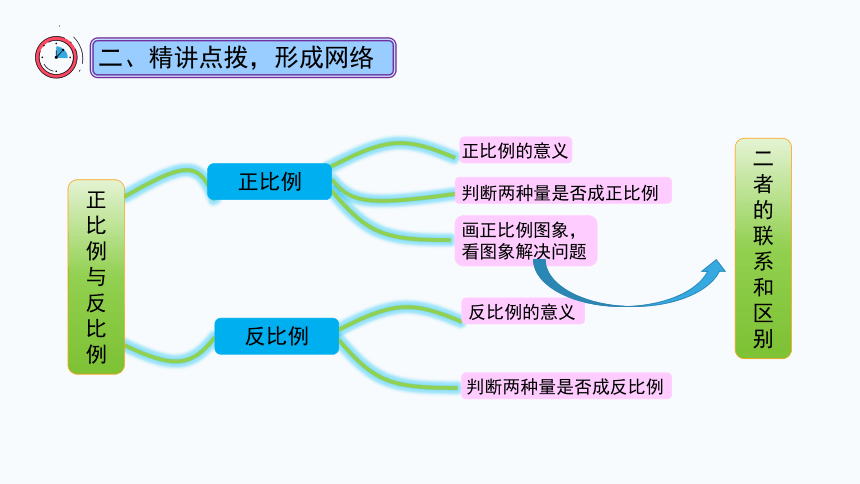
正比例与反比例
正比例
判断两种量是否成正比例
正比例的意义
画正比例图象,
看图象解决问题
反比例
判断两种量是否成反比例
反比例的意义
二、精讲点拨,形成网络
二者的联系和区别
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种
量中相对应的两个数的比值一定,这两种量就叫做成正比例的量.
它们的关系叫做正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定)
正比例关系可以用下面的式子表示:
二、精讲点拨,形成网络
1.正比例的意义
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种
量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量.
它们的关系叫做反比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的积(一定)
反比例关系可以用下面的式子表示:
二、精讲点拨,形成网络
2.反比例的意义
二、精讲点拨,形成网络
3.正比例和反比例的图像
0
2 3 4 5 6 7
1
240
40
80
120
160
200
路程(千米)
0 5 10 15 20 25 30
120
20
40
60
80
100
加工时间(时)
时间(时)
每小时加工数(个)
正比例图像是一条从(0,0)出发的射线。
反比例图像是一条光滑的曲线。
二、精讲点拨,形成网络
3.正比例和反比例的图像
正比例 反比例
相同点
不同点 变化方向
关系式
结果
图像
变化的方向相同,一种量扩大(或缩小),另一种量也随着扩大(或缩小)
都是两种相关联的量,一种量变化,另一种量也随着变化
变化的方向相反,一种量扩大(或缩小),另一种量反而缩小(或扩大)
二、精讲点拨,形成网络
两种量中相对应的两个数的比值,也就是商一定
两种量中相对应的两个数的乘积一定
是一条光滑的曲线
是一条从(0,0)出发的无限延伸的射线
4.正、反比例的联系和区别
二、精讲点拨,形成网络
5.判断正反比例的方法
一看:看两种量是不是相关联的量;(一种量是不是随着另一种量的变化而变化)
二算:根据这两种量所对应的数量关系进行列式计算;
三判断:比值一定成正比例,乘积一定成反比例,和或者差一定,不成比例。
判断:
1.两种相关联的量,不是成正比例就是成反比例。( )
4.圆的面积与半径成反比例。( )
2.如果 ,那么x和y成正比例。( )
3.圆柱体的高一定,底面积和体积成正比例。( )
√
×
×
×
三、应用训练,当堂检测
选择:
1.有一堆煤,烧掉的质量和剩余的质量( )。
A.成正比例 B.成反比例 C. 不成比例
2. 3x=4y,x和y( )。
4.下表中,x与y成反比例,那么☆表示的数是( )
A. 3 B.4 C.5 D.6
3.当( )一定时,平行四边形的底和高成反比例。
A.成正比例 B.成反比例 C.无法判断
A. 底 B. 高 C. 面积 D. 无法确定
x 5 ☆
y 12 15
C
A
C
B
烧掉的质量+剩余的质量=煤的总量(和一定)
平行四边形的底×高=平行四边形的面积
三、应用训练,当堂检测
1.除数一定,被除数和商。( )
2.行一段路,已行的路程和剩下的路程。( )
3.一批纸的张数一定,每本练习本的张数和装订的本数。
( )
4.全班人数一定,出勤人数和出勤率。( )
下面每组题中的两种量是否成比例,并说出理由.
成正比例
不成比例
成反比例
成正比例
已行的路程+剩下的路程=总路程(和一定)
每本练习本的张数×装订的本数=总张数(积一定)
被除数÷除数=商
三、应用训练,当堂检测
解决问题:
一个手机组装车间要完成一批任务,每天组装手机的数量与需要的天数如下表。
(1)每天组装的数量用p表示,需要的天数用t表示。你能用式子表示出
p、t和组装的手机总数之间的关系吗?
组装的手机总数=pt
三、应用训练,当堂检测
(2)p与t成什么比例关系?
(3)如果这批组装任务需要8天完成。每天要组装多少部手机?
因为pt=组装手机的总数=12000(乘积一定),
所以p与t成反比例关系。
500×24÷8=1500(部)
答:每天要组装1500部手机。
三、应用训练,当堂检测
完成任务单上相关习题
四、深化巩固,拓展思维
五、总结收获,分层作业
这节课你有哪些收获呢?
正比例和反比例
(复习课)
人教版小学数学六年级下册第四单元
单位:XXXX
授课人:XXX
课前计算训练营
1.填一填。
4×6=60×( ) 2.4×( )=2×12 36×( )= 1.8×6
3650dm =( )m 1.75时=( )分钟 公顷=( )m
( ):8=0.625=30:( ) = =( )%
24
( )
2.算一算。
2019×0.125×8= 72÷ = 7× ÷7× =
1.5×101-1.5= 6 -3 = 25×4%=
0.87+0.3= 1÷25%= 3.14×90=
0.4
10
0.3
3.65
105
1250
5
48
15
62.5
2019
32
150
9
1
1.17
4
282.6
1
通过复习,进一步认识正比例和反比例的意义,了解正、反比例的联系与区别,能正确判断正、反比例;
2
3
学习目标
通过回顾梳理,感悟知识之间的联系,建构正比例、反比例相关的知识网络;
发展分析、比较、抽象、概括的能力,激发探索数学知识和规律的兴趣。
1.结合思维导图,小组内分享关于正比例和反比例的有关知识;
2.叙述各自绘图思路,讨论并总结该部分知识的框架和具体体系;
3.推选代表,展示发言。
一、回顾梳理,集中展示
正比例与反比例
正比例
判断两种量是否成正比例
正比例的意义
画正比例图象,
看图象解决问题
反比例
判断两种量是否成反比例
反比例的意义
二、精讲点拨,形成网络
二者的联系和区别
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种
量中相对应的两个数的比值一定,这两种量就叫做成正比例的量.
它们的关系叫做正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定)
正比例关系可以用下面的式子表示:
二、精讲点拨,形成网络
1.正比例的意义
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种
量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量.
它们的关系叫做反比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的积(一定)
反比例关系可以用下面的式子表示:
二、精讲点拨,形成网络
2.反比例的意义
二、精讲点拨,形成网络
3.正比例和反比例的图像
0
2 3 4 5 6 7
1
240
40
80
120
160
200
路程(千米)
0 5 10 15 20 25 30
120
20
40
60
80
100
加工时间(时)
时间(时)
每小时加工数(个)
正比例图像是一条从(0,0)出发的射线。
反比例图像是一条光滑的曲线。
二、精讲点拨,形成网络
3.正比例和反比例的图像
正比例 反比例
相同点
不同点 变化方向
关系式
结果
图像
变化的方向相同,一种量扩大(或缩小),另一种量也随着扩大(或缩小)
都是两种相关联的量,一种量变化,另一种量也随着变化
变化的方向相反,一种量扩大(或缩小),另一种量反而缩小(或扩大)
二、精讲点拨,形成网络
两种量中相对应的两个数的比值,也就是商一定
两种量中相对应的两个数的乘积一定
是一条光滑的曲线
是一条从(0,0)出发的无限延伸的射线
4.正、反比例的联系和区别
二、精讲点拨,形成网络
5.判断正反比例的方法
一看:看两种量是不是相关联的量;(一种量是不是随着另一种量的变化而变化)
二算:根据这两种量所对应的数量关系进行列式计算;
三判断:比值一定成正比例,乘积一定成反比例,和或者差一定,不成比例。
判断:
1.两种相关联的量,不是成正比例就是成反比例。( )
4.圆的面积与半径成反比例。( )
2.如果 ,那么x和y成正比例。( )
3.圆柱体的高一定,底面积和体积成正比例。( )
√
×
×
×
三、应用训练,当堂检测
选择:
1.有一堆煤,烧掉的质量和剩余的质量( )。
A.成正比例 B.成反比例 C. 不成比例
2. 3x=4y,x和y( )。
4.下表中,x与y成反比例,那么☆表示的数是( )
A. 3 B.4 C.5 D.6
3.当( )一定时,平行四边形的底和高成反比例。
A.成正比例 B.成反比例 C.无法判断
A. 底 B. 高 C. 面积 D. 无法确定
x 5 ☆
y 12 15
C
A
C
B
烧掉的质量+剩余的质量=煤的总量(和一定)
平行四边形的底×高=平行四边形的面积
三、应用训练,当堂检测
1.除数一定,被除数和商。( )
2.行一段路,已行的路程和剩下的路程。( )
3.一批纸的张数一定,每本练习本的张数和装订的本数。
( )
4.全班人数一定,出勤人数和出勤率。( )
下面每组题中的两种量是否成比例,并说出理由.
成正比例
不成比例
成反比例
成正比例
已行的路程+剩下的路程=总路程(和一定)
每本练习本的张数×装订的本数=总张数(积一定)
被除数÷除数=商
三、应用训练,当堂检测
解决问题:
一个手机组装车间要完成一批任务,每天组装手机的数量与需要的天数如下表。
(1)每天组装的数量用p表示,需要的天数用t表示。你能用式子表示出
p、t和组装的手机总数之间的关系吗?
组装的手机总数=pt
三、应用训练,当堂检测
(2)p与t成什么比例关系?
(3)如果这批组装任务需要8天完成。每天要组装多少部手机?
因为pt=组装手机的总数=12000(乘积一定),
所以p与t成反比例关系。
500×24÷8=1500(部)
答:每天要组装1500部手机。
三、应用训练,当堂检测
完成任务单上相关习题
四、深化巩固,拓展思维
五、总结收获,分层作业
这节课你有哪些收获呢?
