第二十章 数据的分析 评估测试卷(含答案)2024-2025学年数学人教版八年级下册
文档属性
| 名称 | 第二十章 数据的分析 评估测试卷(含答案)2024-2025学年数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 128.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:19:37 | ||
图片预览


文档简介
第二十章 数据的分析评估测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.某同学要统计本校图书馆最受学生欢迎的图书种类,以下是打乱顺序的统计步骤:①从扇形图中分析出最受学生欢迎的种类;②去图书馆收集学生借阅图书的记录;③绘制扇形图来表示各个种类所占的百分比;④整理借阅图书记录并绘制频数分布表.正确统计步骤的顺序是 ( )
A.①③②④ B.②④③①
C.④③①② D.②①④③
2.下表为嘉淇八年级下学年的年级排名.若添加数据9后,该组数据的平均数增加了,则嘉淇的八下三调考试年级排名为 ( )
考试 八下一调 八下二调 八下三调 八下期末
年级排名 6 6 4
A.26 B.19 C.1 D.38
3.某企业参加“科技创新企业百强”评选,创新能力、创新价值、创新影响三项得分分别为8分,9分,7分.若将三项得分依次按5∶3∶2的比例计算总成绩,则该企业的总成绩为 ( )
A.8分 B.8.1分 C.8.2分 D.8.3分
4.小明根据演讲比赛中九位评委所给的分数制作了如下表格:
中位数 众数 方差
8.3 8.1 0.15
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是 ( )
A.平均数 B.众数 C.中位数 D.方差
5.在体育中考模拟测试中,九年级某班的7名女生仰卧起坐的成绩(单位:个)分别为52,54,55,46,52,53,52.这组数据的众数和中位数分别是 ( )
A.52,54 B.53,54 C.52,52 D.52,56
6.若一组数据2,3,5,6,a有唯一众数,且众数与中位数相等,则a的值为 ( )
A.3 B.5 C.3或5 D.3或4
7.一组大于1的正整数5,7,3,m,7,6的中位数是5.5;唯一的众数是7,则这组数据的平均数是 ( )
A. B. C.5或 D.5或
8.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如表所示:
选手 甲 乙 丙 丁
平均数 7 8 8 7
方差 0.9 1.1 0.9 1
则这四位选手中成绩好且发挥最稳定的是 ( )
A.甲 B.乙
C.丙 D.丁
9.已知一组数据x1,x2,x3,x4的方差为5,则x1-1,x2-1,x3-1,x4-1的方差为 ( )
A.5 B.4
C.3 D.1
10.一组数据:2,5,2,3,若添加一个数据3,则不发生变化的统计量是 ( )
A.平均数 B.中位数
C.众数 D.方差
11.(2024遵化月考)某班50名同学进行党史知识竞赛,测试成绩统计如表,其中有两个数据被遮盖.关于成绩的统计量中,与被遮盖的数据无关的是 ( )
成绩/分 91 92 93 94 95 96 97 98 99 100
人数 ■ ■ 1 2 3 5 6 8 10 12
A.众数、中位数 B.众数、平均数
C.中位数、平均数 D.众数、方差
12.甲、乙两组各有12名学生,各组长绘制了本组5月份家庭用水量的统计图表如下.
甲组5月份12户家庭用水量统计表
用水量/t 4 5 6 9
户数 4 5 2 1
乙组5月份12户家庭用水量统计图
比较5月份两组家庭用水量的中位数,下列说法正确的是 ( )
A.甲组比乙组大 B.甲、乙两组相等
C.乙组比甲组大 D.无法判断
二、填空题(本大题共4个小题,每小题3分,共12分)
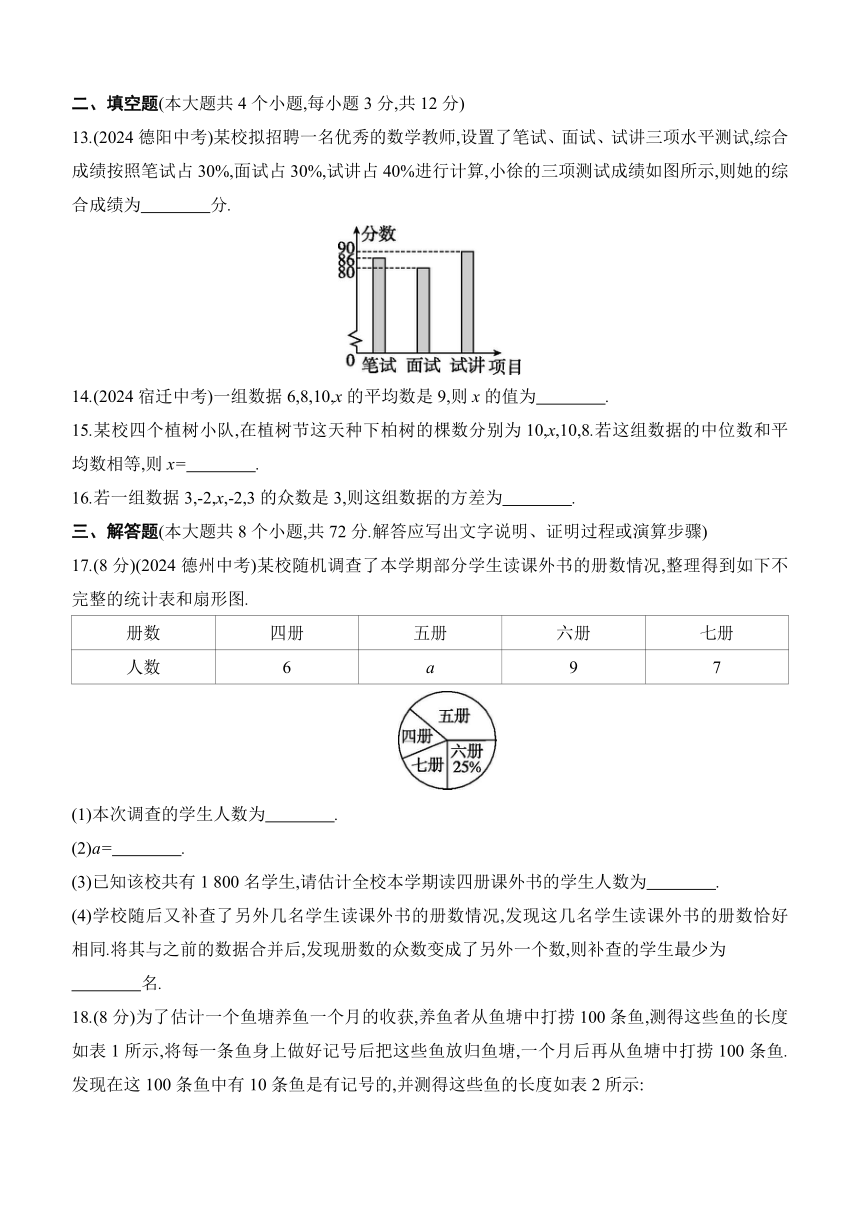
13.(2024德阳中考)某校拟招聘一名优秀的数学教师,设置了笔试、面试、试讲三项水平测试,综合成绩按照笔试占30%,面试占30%,试讲占40%进行计算,小徐的三项测试成绩如图所示,则她的综合成绩为 分.
14.(2024宿迁中考)一组数据6,8,10,x的平均数是9,则x的值为 .
15.某校四个植树小队,在植树节这天种下柏树的棵数分别为10,x,10,8.若这组数据的中位数和平均数相等,则x= .
16.若一组数据3,-2,x,-2,3的众数是3,则这组数据的方差为 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)(2024德州中考)某校随机调查了本学期部分学生读课外书的册数情况,整理得到如下不完整的统计表和扇形图.
册数 四册 五册 六册 七册
人数 6 a 9 7
(1)本次调查的学生人数为 .
(2)a= .
(3)已知该校共有1 800名学生,请估计全校本学期读四册课外书的学生人数为 .
(4)学校随后又补查了另外几名学生读课外书的册数情况,发现这几名学生读课外书的册数恰好相同.将其与之前的数据合并后,发现册数的众数变成了另外一个数,则补查的学生最少为
名.
18.(8分)为了估计一个鱼塘养鱼一个月的收获,养鱼者从鱼塘中打捞100条鱼,测得这些鱼的长度如表1所示,将每一条鱼身上做好记号后把这些鱼放归鱼塘,一个月后再从鱼塘中打捞100条鱼.发现在这100条鱼中有10条鱼是有记号的,并测得这些鱼的长度如表2所示:
表1
长度/cm 13 14 15 16 17
条数 10 20 30 20 20
表2
长度/cm 17 18 19 22
条数 2 2 4 2
(1)估计这个鱼塘有多少条鱼.
(2)设增长1 cm长的鱼约增重80 g,估计这个鱼塘的鱼一个月能增重多少千克.
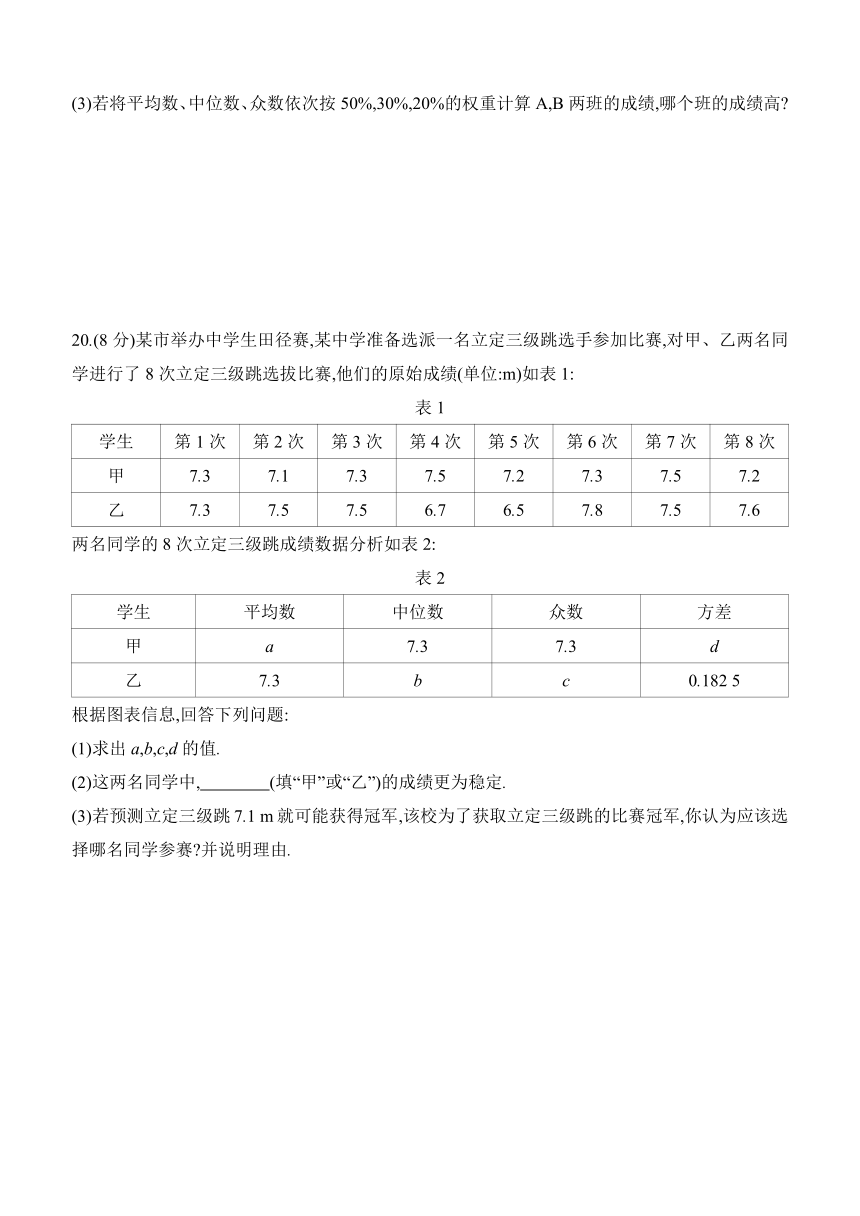
19.(8分)6月5日是世界环境日,为增强学生的环境保护意识,某学校举行了“环保主题知识竞赛”.现从该校A,B两班参赛学生中各随机抽取10名学生的成绩,并进行整理分析,下面给出了部分信息:
B班10名学生的成绩为7,8,8,8,8,9,9,9,10,10.
A,B两班抽取学生竞赛成绩统计表
班级 平均数 中位数 众数
A班 8.6 9 a
B班 8.6 b 8
A班抽取学生竞赛成绩条形图
根据以上信息,解答下列问题:
(1)a= ,b= .
(2)根据以上数据,你认为该校A,B两班中,哪个班级学生知识竞赛成绩更优异 请说明理由.
(3)若将平均数、中位数、众数依次按50%,30%,20%的权重计算A,B两班的成绩,哪个班的成绩高
20.(8分)某市举办中学生田径赛,某中学准备选派一名立定三级跳选手参加比赛,对甲、乙两名同学进行了8次立定三级跳选拔比赛,他们的原始成绩(单位:m)如表1:
表1
学生 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次
甲 7.3 7.1 7.3 7.5 7.2 7.3 7.5 7.2
乙 7.3 7.5 7.5 6.7 6.5 7.8 7.5 7.6
两名同学的8次立定三级跳成绩数据分析如表2:
表2
学生 平均数 中位数 众数 方差
甲 a 7.3 7.3 d
乙 7.3 b c 0.182 5
根据图表信息,回答下列问题:
(1)求出a,b,c,d的值.
(2)这两名同学中, (填“甲”或“乙”)的成绩更为稳定.
(3)若预测立定三级跳7.1 m就可能获得冠军,该校为了获取立定三级跳的比赛冠军,你认为应该选择哪名同学参赛 并说明理由.
21.(10分)某工厂车间共有20名工人,调查每名工人的日均生产能力,获得数据如下表:
工人日均生产件数 8 10 12 13
人数 6 2 4 8
根据以上信息,回答下列问题:
(1)20名工人的日均生产件数的众数是 ,中位数是 .
(2)计算这20名工人的日均生产件数的平均数.
(3)若要使60%的工人都能完成任务,应选什么统计量(平均数、中位数、众数)作为日均生产件数的定额 请说明理由.
22.(10分)为鼓励学生积极加入中国共青团组织,某学校团委在八、九年级各抽取50名学生开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分10分.竞赛成绩如图所示.
(1)请根据图表中的信息,回答下列问题.
年级 平均数 众数 中位数 方差
八年级 8 7 b 1.88
九年级 8 a 8 c
①表中的a= ,b= ,c= .
②现要给成绩突出的年级颁奖,如果分别从众数和方差两个角度来分析,你认为应该给哪个年级颁奖
(2)若规定成绩10分获一等奖,9分获二等奖,8分获三等奖,请通过计算说明哪个年级的获奖率高
23.(10分)甲、乙、丙三位同学参加数学综合素质测试.各项成绩(单位:分)如下:
同学 数与代数 图形与几何 概率与统计 综合
甲 91 88 90 x
乙 70 92 99 y
丙 z 79 93 251
(1)请写出表格中三个未知数的平均值: .
(2)甲、乙、丙三位同学单科成绩的中位数分别为 .
(3)若数与代数、图形与几何、概率与统计成绩按照比例3∶4∶3来计算,谁更有希望去参加市数学大赛 请说明理由.
24.(10分)蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分10分):
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分(满分10分)统计图:
c.配送速度和服务质量得分统计表:
快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 7.8 m 7
乙 8 8 7
根据以上信息,回答下列问题:
(1)表格中的m= ; (填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司 请说明理由.
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息 (列出一条即可)
【详解答案】
1.B 解析:正确统计步骤的顺序是②去图书馆收集学生借阅图书的记录;④整理借阅图书记录并绘制频数分布表;③绘制扇形图来表示各个种类所占的百分比;①从扇形图中分析出最受学生欢迎的种类.故正确统计步骤的顺序是②④③①.故选B.
2.C 解析:设嘉淇的八下三调考试年级排名为x,依题意有(6+6+x+4+9)÷5=(6+6+x+4)÷4+.解得x=1.故嘉淇的八下三调考试年级排名为1.故选C.
3.B 解析:该企业的总成绩为8×+9×+7×=8.1(分).故选B.
4.C 解析:去掉一个最高分和一个最低分,对中位数不产生影响,故中位数不会发生变化.故选C.
5.C 解析:∵这组数据中,52出现次数最多,∴众数是52.将这组数据从小到大排列:46,52,52,52,53,54,55,则中位数为52.故选C.
6.C 解析:∵数据2,3,5,6,a有唯一众数,且众数与中位数相等,∴a应该属于排序后第3位,且与第二或第四个数相同.∴a=3或5.故选C.
7.C 解析:根据题意,已知众数、中位数和其中的五个数,可以推出m为2或4.∴这组数据的平均数是=5或=.故选C.
8.C 解析:∵乙、丙的平均数高于甲、丁,
∴乙、丙的成绩较好,又∵丙的方差比乙小,
∴这四位选手中成绩好且发挥最稳定的是丙.故选C.
9.A 解析:∵数据x1,x2,x3,x4与数据x1-1,x2-1,x3-1,x4-1的波动程度相同,数据x1,x2,x3,x4的方差是5,
∴数据x1-1,x2-1,x3-1,x4-1的方差是5.故选A.
10.A 解析:由这组数据:2,5,2,3,可得平均数是=3,中位数是=2.5,众数是2,方差是
×[(2-3)2+(5-3)2+(2-3)2+(3-3)2]=,
加入数据3后,这组数据变为2,2,3,3,5,平均数是=3,中位数是3,众数是2和3,方差是
×[(2-3)2+(5-3)2+(2-3)2+(3-3)2+(3-3)2]=.∴不发生变化的是平均数.故选A.
11.A 解析:由表格数据可知,成绩为91分、92分的同学为50-(12+10+8+6+5+3+2+1)=3(名),则在这组数据中,100出现次数最多,因此成绩的众数是100,成绩从小到大排列后处在第25,26位的两个数都是98,因此成绩的中位数是98,因此中位数和众数与被遮盖的数据无关.故选A.
12.B 解析:由统计表知,甲组家庭用水量的中位数为=5(t),乙组家庭用水量为4 t和6 t的分别有12×=3(户),用水量为7 t的有12×=2(户),则用水量为5 t的有12-(3+3+2)=4(户),∴乙组家庭用水量的中位数为=5(t).∴甲组和乙组家庭用水量的中位数相等.故选B.
13.85.8 解析:她的综合成绩为86×30%+80×30%+90×40%=85.8(分).
14.12 解析:∵一组数据6,8,10,x的平均数是9,∴=9.解得x=12.
15.12或8 解析:∵这组数据的中位数和平均数相等,∴=10或9.解得x=12或8.
16.6 解析:∵数据3,-2,x,-2,3的众数是3,∴x=3.∴这组数据为3,-2,3,-2,3.∴这组数据的平均数为
=1.∴这组数据的方差为×[2×(-2-1)2+3×(3-1)2]=6.
17.解:(1)36 (2)14 (3)300 (4)6
解析:(1)本次调查的学生人数为
9÷25%=36.
(2)a=36-6-9-7=14.
(3)估计全校本学期读四册课外书的学生人数为1 800×=300.
(4)补查前读课外书册数最多的是五册,
∴补查前读课外书册数的众数为5.
∵补查的几名学生读课外书的册数恰好相同,且补查后读课外书册数的众数变成了另外一个数,
∴补查的学生最少为14-9+1=6(名).
18.解:(1)设这个鱼塘有n条鱼.
依题意.得=,解得n=1 000.
经检验,n=1 000是原方程的根,且符合题意.
答:估计这个鱼塘中有1 000条鱼.
(2)打捞的100条鱼中每条鱼的平均长度为
=15.2(cm).
一个月后打捞有记号的10条鱼中每条鱼的平均长度为
=19(cm).
这个鱼塘每条鱼平均增长的长度约为
19-15.2=3.8(cm),
这个鱼塘的鱼一个月约能增重
3.8×80×1 000=304 000(g)=304(kg).
答:估计这个鱼塘的鱼一个月能增重304 kg.
19.解:(1)10 8.5
(2)A班学生知识竞赛成绩更优异.理由如下:
∵A,B两班学生知识竞赛成绩的平均数相同,但A班学生知识竞赛成绩的中位数大于B班学生知识竞赛成绩的中位数,A班学生知识竞赛成绩的众数大于B班学生知识竞赛成绩的众数,
∴A班学生知识竞赛成绩更优异.
(3)A班的成绩为
8.6×50%+9×30%+10×20%=9(分),
B班的成绩为
8.6×50%+8.5×30%+8×20%=8.45(分),
∵9>8.45,∴A班的成绩高.
20.解:(1)由题意,得a=×(7.3×3+7.1+7.5×2+7.2×2)=7.3;
b==7.5;c=7.5;
d=×[3×(7.3-7.3)2+(7.1-7.3)2+2×(7.5-7.3)2+2×(7.2-7.3)2]=0.017 5.
(2)甲
(3)应选择甲同学参赛.理由如下:
∵预测立定三级跳7.1 m就可能获得冠军,
∴成绩在7.1 m或7.1 m以上的次数甲多,故选择甲同学参赛.
21.解:(1)13 12
(2)=11.
答:这20名工人的日均生产件数的平均数为11.
(3)选择中位数或平均数作为日均生产件数的定额.理由如下:
∵20×60%=12(人),
日均生产12件及12件以上的有4+8=12(人),
∴只需日均生产件数的定额大于10件且小于或等于12件即可.
∴选择中位数或平均数作为日均生产件数的定额.
22.解:(1)①8 8 1.56
②∵从众数角度看,八年级的众数为7分,九年级的众数为8分,
∴应该给九年级颁奖.
∵从方差角度看,八年级的方差为1.88,九年级的方差为1.56,
又∵两个年级的平均数相同,九年级的成绩波动小,
∴应该给九年级颁奖.
故如果分别从众数和方差两个角度来分析,应该给九年级颁奖.
(2)八年级的获奖率为
(10+7+11)÷50=56%,
九年级的获奖率为
(14+13+6)÷50=66%,
∵66%>56%,∴九年级的获奖率高.
23.解:(1)203 (2)90,92,79
(3)甲更有希望去参加市数学大赛.理由如下:
甲的平均成绩为
=89.5(分),
乙的平均成绩为
=87.5(分),
丙的平均成绩为
=83.2(分),
∵89.5>87.5>83.2,
∴甲更有希望去参加市数学大赛.
24.解:(1)7.5 <
(2)(答案不唯一)小丽应选择甲公司.理由如下:
∵配送速度甲和乙的得分相差不大,服务质量得分中甲和乙的平均数相同,但是甲的方差明显小于乙的方差,
∴甲公司更稳定.
∴小丽应选择甲公司.
(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.某同学要统计本校图书馆最受学生欢迎的图书种类,以下是打乱顺序的统计步骤:①从扇形图中分析出最受学生欢迎的种类;②去图书馆收集学生借阅图书的记录;③绘制扇形图来表示各个种类所占的百分比;④整理借阅图书记录并绘制频数分布表.正确统计步骤的顺序是 ( )
A.①③②④ B.②④③①
C.④③①② D.②①④③
2.下表为嘉淇八年级下学年的年级排名.若添加数据9后,该组数据的平均数增加了,则嘉淇的八下三调考试年级排名为 ( )
考试 八下一调 八下二调 八下三调 八下期末
年级排名 6 6 4
A.26 B.19 C.1 D.38
3.某企业参加“科技创新企业百强”评选,创新能力、创新价值、创新影响三项得分分别为8分,9分,7分.若将三项得分依次按5∶3∶2的比例计算总成绩,则该企业的总成绩为 ( )
A.8分 B.8.1分 C.8.2分 D.8.3分
4.小明根据演讲比赛中九位评委所给的分数制作了如下表格:
中位数 众数 方差
8.3 8.1 0.15
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是 ( )
A.平均数 B.众数 C.中位数 D.方差
5.在体育中考模拟测试中,九年级某班的7名女生仰卧起坐的成绩(单位:个)分别为52,54,55,46,52,53,52.这组数据的众数和中位数分别是 ( )
A.52,54 B.53,54 C.52,52 D.52,56
6.若一组数据2,3,5,6,a有唯一众数,且众数与中位数相等,则a的值为 ( )
A.3 B.5 C.3或5 D.3或4
7.一组大于1的正整数5,7,3,m,7,6的中位数是5.5;唯一的众数是7,则这组数据的平均数是 ( )
A. B. C.5或 D.5或
8.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如表所示:
选手 甲 乙 丙 丁
平均数 7 8 8 7
方差 0.9 1.1 0.9 1
则这四位选手中成绩好且发挥最稳定的是 ( )
A.甲 B.乙
C.丙 D.丁
9.已知一组数据x1,x2,x3,x4的方差为5,则x1-1,x2-1,x3-1,x4-1的方差为 ( )
A.5 B.4
C.3 D.1
10.一组数据:2,5,2,3,若添加一个数据3,则不发生变化的统计量是 ( )
A.平均数 B.中位数
C.众数 D.方差
11.(2024遵化月考)某班50名同学进行党史知识竞赛,测试成绩统计如表,其中有两个数据被遮盖.关于成绩的统计量中,与被遮盖的数据无关的是 ( )
成绩/分 91 92 93 94 95 96 97 98 99 100
人数 ■ ■ 1 2 3 5 6 8 10 12
A.众数、中位数 B.众数、平均数
C.中位数、平均数 D.众数、方差
12.甲、乙两组各有12名学生,各组长绘制了本组5月份家庭用水量的统计图表如下.
甲组5月份12户家庭用水量统计表
用水量/t 4 5 6 9
户数 4 5 2 1
乙组5月份12户家庭用水量统计图
比较5月份两组家庭用水量的中位数,下列说法正确的是 ( )
A.甲组比乙组大 B.甲、乙两组相等
C.乙组比甲组大 D.无法判断
二、填空题(本大题共4个小题,每小题3分,共12分)
13.(2024德阳中考)某校拟招聘一名优秀的数学教师,设置了笔试、面试、试讲三项水平测试,综合成绩按照笔试占30%,面试占30%,试讲占40%进行计算,小徐的三项测试成绩如图所示,则她的综合成绩为 分.
14.(2024宿迁中考)一组数据6,8,10,x的平均数是9,则x的值为 .
15.某校四个植树小队,在植树节这天种下柏树的棵数分别为10,x,10,8.若这组数据的中位数和平均数相等,则x= .
16.若一组数据3,-2,x,-2,3的众数是3,则这组数据的方差为 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)(2024德州中考)某校随机调查了本学期部分学生读课外书的册数情况,整理得到如下不完整的统计表和扇形图.
册数 四册 五册 六册 七册
人数 6 a 9 7
(1)本次调查的学生人数为 .
(2)a= .
(3)已知该校共有1 800名学生,请估计全校本学期读四册课外书的学生人数为 .
(4)学校随后又补查了另外几名学生读课外书的册数情况,发现这几名学生读课外书的册数恰好相同.将其与之前的数据合并后,发现册数的众数变成了另外一个数,则补查的学生最少为
名.
18.(8分)为了估计一个鱼塘养鱼一个月的收获,养鱼者从鱼塘中打捞100条鱼,测得这些鱼的长度如表1所示,将每一条鱼身上做好记号后把这些鱼放归鱼塘,一个月后再从鱼塘中打捞100条鱼.发现在这100条鱼中有10条鱼是有记号的,并测得这些鱼的长度如表2所示:
表1
长度/cm 13 14 15 16 17
条数 10 20 30 20 20
表2
长度/cm 17 18 19 22
条数 2 2 4 2
(1)估计这个鱼塘有多少条鱼.
(2)设增长1 cm长的鱼约增重80 g,估计这个鱼塘的鱼一个月能增重多少千克.
19.(8分)6月5日是世界环境日,为增强学生的环境保护意识,某学校举行了“环保主题知识竞赛”.现从该校A,B两班参赛学生中各随机抽取10名学生的成绩,并进行整理分析,下面给出了部分信息:
B班10名学生的成绩为7,8,8,8,8,9,9,9,10,10.
A,B两班抽取学生竞赛成绩统计表
班级 平均数 中位数 众数
A班 8.6 9 a
B班 8.6 b 8
A班抽取学生竞赛成绩条形图
根据以上信息,解答下列问题:
(1)a= ,b= .
(2)根据以上数据,你认为该校A,B两班中,哪个班级学生知识竞赛成绩更优异 请说明理由.
(3)若将平均数、中位数、众数依次按50%,30%,20%的权重计算A,B两班的成绩,哪个班的成绩高
20.(8分)某市举办中学生田径赛,某中学准备选派一名立定三级跳选手参加比赛,对甲、乙两名同学进行了8次立定三级跳选拔比赛,他们的原始成绩(单位:m)如表1:
表1
学生 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次
甲 7.3 7.1 7.3 7.5 7.2 7.3 7.5 7.2
乙 7.3 7.5 7.5 6.7 6.5 7.8 7.5 7.6
两名同学的8次立定三级跳成绩数据分析如表2:
表2
学生 平均数 中位数 众数 方差
甲 a 7.3 7.3 d
乙 7.3 b c 0.182 5
根据图表信息,回答下列问题:
(1)求出a,b,c,d的值.
(2)这两名同学中, (填“甲”或“乙”)的成绩更为稳定.
(3)若预测立定三级跳7.1 m就可能获得冠军,该校为了获取立定三级跳的比赛冠军,你认为应该选择哪名同学参赛 并说明理由.
21.(10分)某工厂车间共有20名工人,调查每名工人的日均生产能力,获得数据如下表:
工人日均生产件数 8 10 12 13
人数 6 2 4 8
根据以上信息,回答下列问题:
(1)20名工人的日均生产件数的众数是 ,中位数是 .
(2)计算这20名工人的日均生产件数的平均数.
(3)若要使60%的工人都能完成任务,应选什么统计量(平均数、中位数、众数)作为日均生产件数的定额 请说明理由.
22.(10分)为鼓励学生积极加入中国共青团组织,某学校团委在八、九年级各抽取50名学生开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分10分.竞赛成绩如图所示.
(1)请根据图表中的信息,回答下列问题.
年级 平均数 众数 中位数 方差
八年级 8 7 b 1.88
九年级 8 a 8 c
①表中的a= ,b= ,c= .
②现要给成绩突出的年级颁奖,如果分别从众数和方差两个角度来分析,你认为应该给哪个年级颁奖
(2)若规定成绩10分获一等奖,9分获二等奖,8分获三等奖,请通过计算说明哪个年级的获奖率高
23.(10分)甲、乙、丙三位同学参加数学综合素质测试.各项成绩(单位:分)如下:
同学 数与代数 图形与几何 概率与统计 综合
甲 91 88 90 x
乙 70 92 99 y
丙 z 79 93 251
(1)请写出表格中三个未知数的平均值: .
(2)甲、乙、丙三位同学单科成绩的中位数分别为 .
(3)若数与代数、图形与几何、概率与统计成绩按照比例3∶4∶3来计算,谁更有希望去参加市数学大赛 请说明理由.
24.(10分)蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分10分):
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分(满分10分)统计图:
c.配送速度和服务质量得分统计表:
快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 7.8 m 7
乙 8 8 7
根据以上信息,回答下列问题:
(1)表格中的m= ; (填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司 请说明理由.
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息 (列出一条即可)
【详解答案】
1.B 解析:正确统计步骤的顺序是②去图书馆收集学生借阅图书的记录;④整理借阅图书记录并绘制频数分布表;③绘制扇形图来表示各个种类所占的百分比;①从扇形图中分析出最受学生欢迎的种类.故正确统计步骤的顺序是②④③①.故选B.
2.C 解析:设嘉淇的八下三调考试年级排名为x,依题意有(6+6+x+4+9)÷5=(6+6+x+4)÷4+.解得x=1.故嘉淇的八下三调考试年级排名为1.故选C.
3.B 解析:该企业的总成绩为8×+9×+7×=8.1(分).故选B.
4.C 解析:去掉一个最高分和一个最低分,对中位数不产生影响,故中位数不会发生变化.故选C.
5.C 解析:∵这组数据中,52出现次数最多,∴众数是52.将这组数据从小到大排列:46,52,52,52,53,54,55,则中位数为52.故选C.
6.C 解析:∵数据2,3,5,6,a有唯一众数,且众数与中位数相等,∴a应该属于排序后第3位,且与第二或第四个数相同.∴a=3或5.故选C.
7.C 解析:根据题意,已知众数、中位数和其中的五个数,可以推出m为2或4.∴这组数据的平均数是=5或=.故选C.
8.C 解析:∵乙、丙的平均数高于甲、丁,
∴乙、丙的成绩较好,又∵丙的方差比乙小,
∴这四位选手中成绩好且发挥最稳定的是丙.故选C.
9.A 解析:∵数据x1,x2,x3,x4与数据x1-1,x2-1,x3-1,x4-1的波动程度相同,数据x1,x2,x3,x4的方差是5,
∴数据x1-1,x2-1,x3-1,x4-1的方差是5.故选A.
10.A 解析:由这组数据:2,5,2,3,可得平均数是=3,中位数是=2.5,众数是2,方差是
×[(2-3)2+(5-3)2+(2-3)2+(3-3)2]=,
加入数据3后,这组数据变为2,2,3,3,5,平均数是=3,中位数是3,众数是2和3,方差是
×[(2-3)2+(5-3)2+(2-3)2+(3-3)2+(3-3)2]=.∴不发生变化的是平均数.故选A.
11.A 解析:由表格数据可知,成绩为91分、92分的同学为50-(12+10+8+6+5+3+2+1)=3(名),则在这组数据中,100出现次数最多,因此成绩的众数是100,成绩从小到大排列后处在第25,26位的两个数都是98,因此成绩的中位数是98,因此中位数和众数与被遮盖的数据无关.故选A.
12.B 解析:由统计表知,甲组家庭用水量的中位数为=5(t),乙组家庭用水量为4 t和6 t的分别有12×=3(户),用水量为7 t的有12×=2(户),则用水量为5 t的有12-(3+3+2)=4(户),∴乙组家庭用水量的中位数为=5(t).∴甲组和乙组家庭用水量的中位数相等.故选B.
13.85.8 解析:她的综合成绩为86×30%+80×30%+90×40%=85.8(分).
14.12 解析:∵一组数据6,8,10,x的平均数是9,∴=9.解得x=12.
15.12或8 解析:∵这组数据的中位数和平均数相等,∴=10或9.解得x=12或8.
16.6 解析:∵数据3,-2,x,-2,3的众数是3,∴x=3.∴这组数据为3,-2,3,-2,3.∴这组数据的平均数为
=1.∴这组数据的方差为×[2×(-2-1)2+3×(3-1)2]=6.
17.解:(1)36 (2)14 (3)300 (4)6
解析:(1)本次调查的学生人数为
9÷25%=36.
(2)a=36-6-9-7=14.
(3)估计全校本学期读四册课外书的学生人数为1 800×=300.
(4)补查前读课外书册数最多的是五册,
∴补查前读课外书册数的众数为5.
∵补查的几名学生读课外书的册数恰好相同,且补查后读课外书册数的众数变成了另外一个数,
∴补查的学生最少为14-9+1=6(名).
18.解:(1)设这个鱼塘有n条鱼.
依题意.得=,解得n=1 000.
经检验,n=1 000是原方程的根,且符合题意.
答:估计这个鱼塘中有1 000条鱼.
(2)打捞的100条鱼中每条鱼的平均长度为
=15.2(cm).
一个月后打捞有记号的10条鱼中每条鱼的平均长度为
=19(cm).
这个鱼塘每条鱼平均增长的长度约为
19-15.2=3.8(cm),
这个鱼塘的鱼一个月约能增重
3.8×80×1 000=304 000(g)=304(kg).
答:估计这个鱼塘的鱼一个月能增重304 kg.
19.解:(1)10 8.5
(2)A班学生知识竞赛成绩更优异.理由如下:
∵A,B两班学生知识竞赛成绩的平均数相同,但A班学生知识竞赛成绩的中位数大于B班学生知识竞赛成绩的中位数,A班学生知识竞赛成绩的众数大于B班学生知识竞赛成绩的众数,
∴A班学生知识竞赛成绩更优异.
(3)A班的成绩为
8.6×50%+9×30%+10×20%=9(分),
B班的成绩为
8.6×50%+8.5×30%+8×20%=8.45(分),
∵9>8.45,∴A班的成绩高.
20.解:(1)由题意,得a=×(7.3×3+7.1+7.5×2+7.2×2)=7.3;
b==7.5;c=7.5;
d=×[3×(7.3-7.3)2+(7.1-7.3)2+2×(7.5-7.3)2+2×(7.2-7.3)2]=0.017 5.
(2)甲
(3)应选择甲同学参赛.理由如下:
∵预测立定三级跳7.1 m就可能获得冠军,
∴成绩在7.1 m或7.1 m以上的次数甲多,故选择甲同学参赛.
21.解:(1)13 12
(2)=11.
答:这20名工人的日均生产件数的平均数为11.
(3)选择中位数或平均数作为日均生产件数的定额.理由如下:
∵20×60%=12(人),
日均生产12件及12件以上的有4+8=12(人),
∴只需日均生产件数的定额大于10件且小于或等于12件即可.
∴选择中位数或平均数作为日均生产件数的定额.
22.解:(1)①8 8 1.56
②∵从众数角度看,八年级的众数为7分,九年级的众数为8分,
∴应该给九年级颁奖.
∵从方差角度看,八年级的方差为1.88,九年级的方差为1.56,
又∵两个年级的平均数相同,九年级的成绩波动小,
∴应该给九年级颁奖.
故如果分别从众数和方差两个角度来分析,应该给九年级颁奖.
(2)八年级的获奖率为
(10+7+11)÷50=56%,
九年级的获奖率为
(14+13+6)÷50=66%,
∵66%>56%,∴九年级的获奖率高.
23.解:(1)203 (2)90,92,79
(3)甲更有希望去参加市数学大赛.理由如下:
甲的平均成绩为
=89.5(分),
乙的平均成绩为
=87.5(分),
丙的平均成绩为
=83.2(分),
∵89.5>87.5>83.2,
∴甲更有希望去参加市数学大赛.
24.解:(1)7.5 <
(2)(答案不唯一)小丽应选择甲公司.理由如下:
∵配送速度甲和乙的得分相差不大,服务质量得分中甲和乙的平均数相同,但是甲的方差明显小于乙的方差,
∴甲公司更稳定.
∴小丽应选择甲公司.
(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)
