第十八章 平行四边形 评估测试卷(含答案)2024-2025学年数学人教版八年级下册
文档属性
| 名称 | 第十八章 平行四边形 评估测试卷(含答案)2024-2025学年数学人教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 236.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 00:00:00 | ||
图片预览



文档简介
第十八章 平行四边形 评估测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
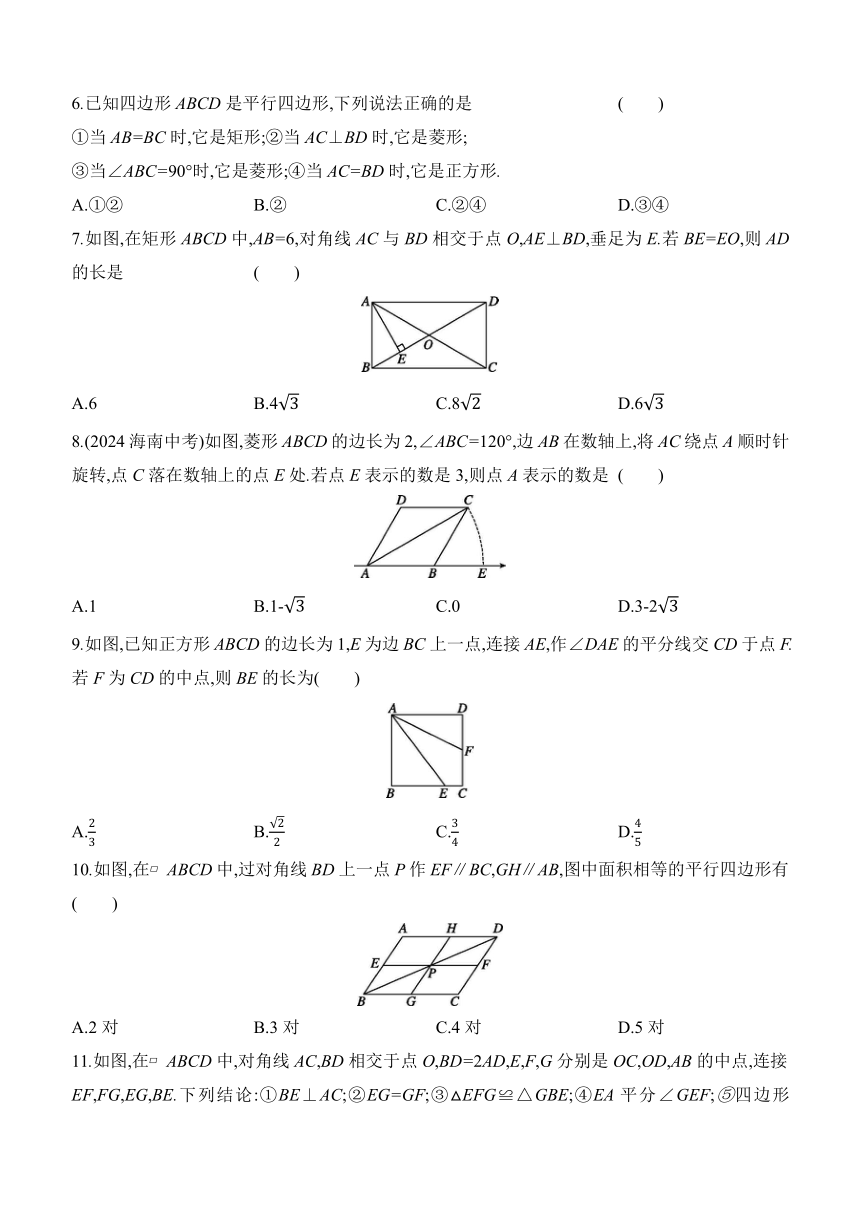
1.(2024沧州盐山县期末)如图,在△ABC中,∠C=90°,AB=13,AC=5,D,E分别是AC,AB的中点,则DE的长是 ( )
A.5 B.6 C.7 D.8
2.如图,在 ABCD中,∠A-∠B=50°,则∠C的度数是 ( )
A.130° B.115° C.65° D.50°
3.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.在此滑动过程中,点P到点O的距离 ( )
A.变小 B.不变 C.变大 D.无法判断
4.如图,若直线m∥n,则下列线段的长可以表示平行线m与n之间的距离的是 ( )
A.AB B.AC C.AD D.DE
5.如图,已知点A的坐标为(-2,2),菱形ABCD的对角线交于坐标原点O,则点C的坐标是 ( )
A.(-2,-2) B.(2,-2) C.(2,-2) D.(-2,-2)
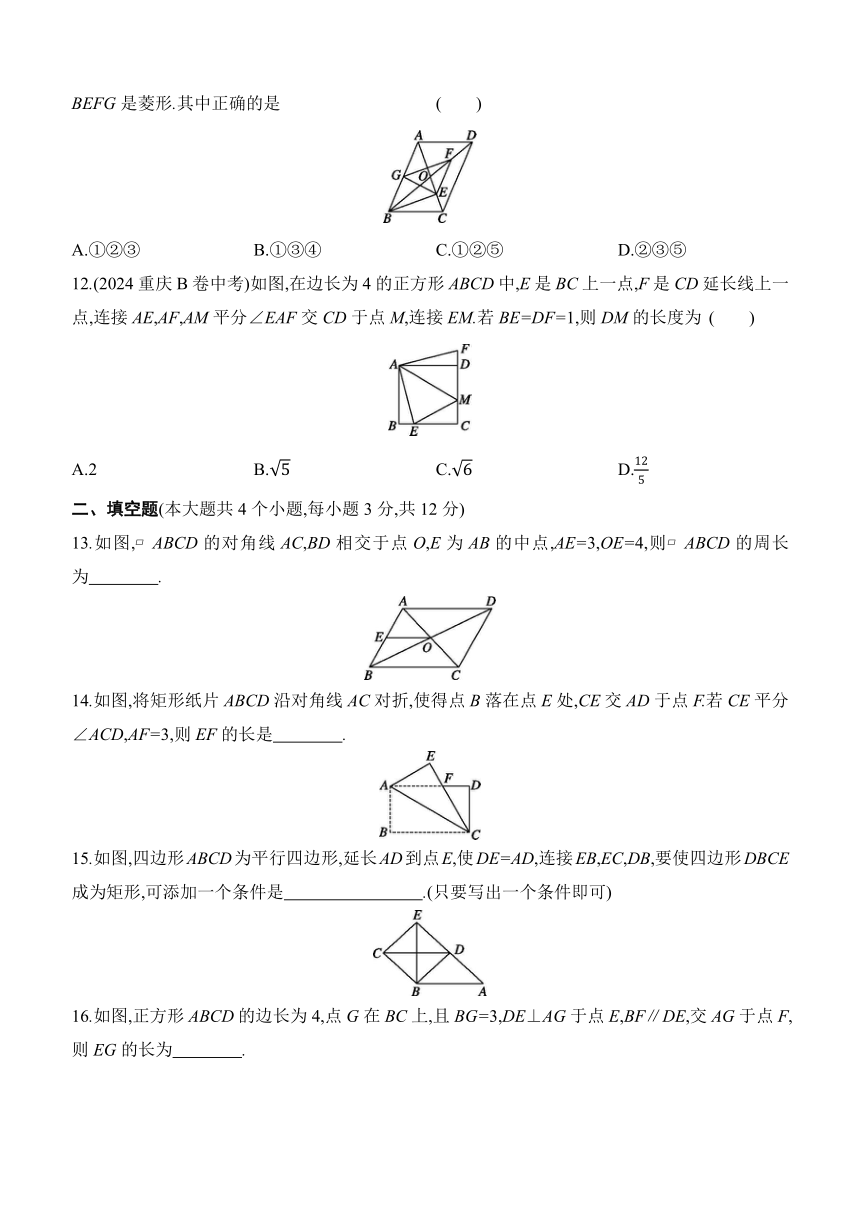
6.已知四边形ABCD是平行四边形,下列说法正确的是 ( )
①当AB=BC时,它是矩形;②当AC⊥BD时,它是菱形;
③当∠ABC=90°时,它是菱形;④当AC=BD时,它是正方形.
A.①② B.② C.②④ D.③④
7.如图,在矩形ABCD中,AB=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E.若BE=EO,则AD的长是 ( )
A.6 B.4 C.8 D.6
8.(2024海南中考)如图,菱形ABCD的边长为2,∠ABC=120°,边AB在数轴上,将AC绕点A顺时针旋转,点C落在数轴上的点E处.若点E表示的数是3,则点A表示的数是 ( )
A.1 B.1- C.0 D.3-2
9.如图,已知正方形ABCD的边长为1,E为边BC上一点,连接AE,作∠DAE的平分线交CD于点F.若F为CD的中点,则BE的长为( )
A. B. C. D.
10.如图,在 ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中面积相等的平行四边形有( )
A.2对 B.3对 C.4对 D.5对
11.如图,在 ABCD中,对角线AC,BD相交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点,连接EF,FG,EG,BE.下列结论:①BE⊥AC;②EG=GF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是 ( )
A.①②③ B.①③④ C.①②⑤ D.②③⑤
12.(2024重庆B卷中考)如图,在边长为4的正方形ABCD中,E是BC上一点,F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M,连接EM.若BE=DF=1,则DM的长度为 ( )
A.2 B. C. D.
二、填空题(本大题共4个小题,每小题3分,共12分)
13.如图, ABCD的对角线AC,BD相交于点O,E为AB的中点,AE=3,OE=4,则 ABCD的周长为 .
14.如图,将矩形纸片ABCD沿对角线AC对折,使得点B落在点E处,CE交AD于点F.若CE平分∠ACD,AF=3,则EF的长是 .
15.如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,要使四边形DBCE成为矩形,可添加一个条件是 .(只要写出一个条件即可)
16.如图,正方形ABCD的边长为4,点G在BC上,且BG=3,DE⊥AG于点E,BF∥DE,交AG于点F,则EG的长为 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)如图,在 ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O.
求证:OE=OF.
18.(8分)如图,在Rt△ABC中,∠ABC=90°,AB(1)求证:四边形AECF是菱形.
(2)若BE=1,CE=4,求EF的长.
19.(8分)将两张长为8、宽为4的矩形纸片按如图所示叠放.
(1)判断四边形AGCH的形状,并说明理由.
(2)求四边形AGCH的面积.
20.(8分)如图,BD平分∠ABF,A是射线BM上一点,过点A作AD∥BN交BG于点D,过点A作AE⊥BN于点E,过点D作DF⊥BN于点F.
(1)求证:四边形AEFD是矩形.
(2)在BF上取点C,使得CF=BE,连接AC,CD.求证:AC⊥BD.
21.(8分)如图,在菱形ABCD中,过点A作AE⊥BC于点E,延长BC至点F,使EF=BC,连接DF.
(1)求证:四边形AEFD是矩形.
(2)若BF=18,DF=6,求CD的长.
22.(8分)如图,在Rt△ABC中,两锐角的平分线AD,BE相交于点O,OF⊥AC于点F,OG⊥BC于点G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
23.(12分)如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.
(1)求证:AK=AH.
(2)求证:四边形AKFH是正方形.
(3)若四边形AKFH的面积为10,CE=1,求点A,E之间的距离.
24.(12分)(2024哈尔滨中考)如图1,四边形ABCD的对角线AC,BD相交于点O,AD∥BC,OA=OC,AB=BC.
(1)求证:四边形ABCD是菱形.
(2)如图2,AB=AC,CH⊥AD于点H,交BD于点E,连接AE,点G在AB上,连接EG交AC于点F.若∠FEC=75°,在不添加任何辅助线的情况下,直接写出四条与线段CE相等的线段(线段CE除外).
图1 图2
【详解答案】
1.B 解析:在△ABC中,∠C=90°,AB=13,AC=5,则BC===12,∵D,E分别是AC,AB的中点,
∴DE=BC=6.故选B.
2.B 解析:∵四边形ABCD是平行四边形,∴∠A=∠C,AD∥BC.∴∠A+∠B=180°.∵∠A-∠B=50°,∴2∠A=230°.∴∠A=115°.∴∠C=115°.故选B.
3.B 解析:如图,连接OP.∵∠AOB=90°,P为AB的中点,∴OP=AB,即在木棍滑动的过程中,点P到点O的距离不发生变化,永远是AB.故选B.
4.B 解析:∵m∥n,AC⊥n,∴AC⊥m.∴AC可以表示平行线m与n之间的距离.故选B.
5.B 解析:∵四边形ABCD为菱形,∴OA=OC,OB=OD.∵点O为坐标原点,∴点A和点C关于原点对称,点B和点D关于原点对称.∵点A的坐标为(-2,2),∴点C的坐标为(2,-2).故选B.
6.B 解析:①若AB=BC,则 ABCD是菱形,选项说法错误;②若AC⊥BD,则 ABCD是菱形,选项说法正确;③若∠ABC=90°,则 ABCD是矩形,选项说法错误;④若AC=BD,则 ABCD是矩形,选项说法错误.综上所述,说法正确的是②.故选B.
7.D 解析:∵四边形ABCD是矩形,∴OA=AC,OB=BD,∠BAD=90°,AC=BD.∴OA=OB.∵AE⊥BD,BE=EO.
∴AE垂直平分OB.∴AB=OA.∴AB=OA=OB=6.∴BD=2OB=12.∴AD==6.故选D.
8.D 解析:如图,过点C作AE的垂线,垂足为F.
∵四边形ABCD是菱形,∴AB=BC=2,AC平分∠DAB,AD∥BC.∴∠DAB+∠ABC=180°.∴∠DAB=180°-∠ABC=
60°.∴∠CAB=∠DAB=30°.∴AC=2CF.∵∠ABC=120°,∴∠CBF=180°-∠ABC=60°.∴∠BCF=90°-∠CBF=30°.∴BF=BC=1.∴在Rt△BCF中,CF===.∴AC=2CF=2.∴AE=AC=2.∵点E表示的数是3,∴点A表示的数是3-2.故选D.
9.C 解析:如图,过点F作FH⊥AE于点H,连接EF.
∵F为CD的中点,
∴DF=CF=.
∵四边形ABCD是正方形,
∴∠D=∠C=∠B=90°.
∵AF是∠DAE的平分线,
∴DF=HF=CF.
∴Rt△ADF≌Rt△AHF(HL).∴AD=AH=1.同理可得Rt△EFH≌Rt△EFC.
∴EH=CE.设CE=EH=x,则AE=1+x,BE=1-x.在Rt△ABE中,AB2+BE2=AE2,∴12+(1-x)2=(1+x)2.解得x=.∴BE=1-=.故选C.
10.B 解析:∵四边形ABCD是平行四边形,∴S△ABD=S△CBD.∵BP是 BEPG的对角线,∴S△BEP=S△BGP.∵PD是 HPFD的对角线,∴S△HPD=S△FPD.∴S△ABD-S△BEP-S△HPD=S△BCD-S△BGP-S△PFD,即S AEPH=S GCFP.∴S ABGH=
S BCFE,同理S AEFD=S GCDH.综上所述,S ABGH=S BCFE,S AEPH=S GCFP,S AEFD=S GCDH,共3对.故选B.
11.B 解析:∵四边形ABCD是平行四边形,∴BO=DO=BD,AD=BC,AB=CD,AB∥CD.又∵BD=2AD,
∴OB=BC=OD=DA.∵E是OC的中点,∴BE⊥AC.故①正确;∵E,F分别是OC,OD的中点,∴EF∥CD,EF=CD.∵G是Rt△ABE斜边AB上的中点,∴GE=AB=AG=BG.∴EG=EF=AG=BG,无法证明EG=GF.故②错误;
∵BG=EF,AB∥CD∥EF,∴四边形BGFE是平行四边形.∴FG=BE.又∵FE=BG,GE=EG,∴△EFG≌△GBE(SSS).故③正确;∵EF∥CD∥AB,∴∠BAC=∠ACD=∠AEF.∵AG=GE,∴∠GAE=∠AEG.∴∠AEG=∠AEF.∴EA平分∠GEF.故④正确;若四边形BEFG是菱形,∴BE=BG=AB.∴∠BAC=30°.与题意不符合,故⑤错误.综上所述,结论正确的是①③④.故选B.
12.D 解析:∵四边形ABCD是正方形,
∴AB=AD,∠ABE=∠ADC=∠ADF=90°.
在Rt△ABE和Rt△ADF中,
∴Rt△ABE≌Rt△ADF(SAS).
∴AE=AF.
∵AM平分∠EAF,
∴∠EAM=∠FAM.
在△AEM和△AFM中,
∴△AEM≌△AFM(SAS).∴EM=FM.
∵四边形ABCD是正方形,
∴BC=CD=4,∠BCD=90°.
设DM=x,则MC=CD-DM=4-x,CE=BC-BE=4-1=3,EM=FM=FD+DM=1+x.
在Rt△MCE中,根据勾股定理,
得EM2=MC2+CE2,
即(1+x)2=(4-x)2+32,
解得x=.故选D.
13.28 解析:∵四边形ABCD是平行四边形,其对角线AC,BD相交于点O,∴AO=CO=AC.∵E为AB的中点,AE=3,∴AB=2AE=6,OE是△ABC的中位线.∴BC=2OE=8.∴ ABCD的周长为2(AB+BC)=2×(6+8)=28.
14. 解析:∵四边形ABCD为矩形,∴∠B=∠D=∠BCD=90°,AB=CD,AD∥BC.∴∠DAC=∠ACB.由折叠可知,AB=AE,∠B=∠E=90°,∠ACB=∠ACE,∴∠CAF=∠ACF.∵AF=3,CE平分∠ACD,∴AF=CF=3,∠ACB=
∠ACF=∠FCD=30°.∴DF=CF=.∵∠B=∠E=90°,AB=AE,∴∠D=∠E=90°,CD=AE.又∵∠CFD=∠AFE,
∴△CDF≌△AEF(AAS).∴EF=DF=.
15.CD=BE(答案不唯一) 解析:∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC.又∵AD=DE,∴DE∥BC,且DE=BC.∴四边形DBCE为平行四边形.添加CD=BE,∴ DBCE为矩形.
16. 解析:∵DE⊥AG,BF∥DE,∴BF⊥AG.∴∠AED=∠BFA=90°.∵四边形ABCD是正方形,∴AB=AD且
∠BAD=∠ADC=90°.∴∠BAF+∠EAD=90°.∵∠EAD+∠ADE=90°,∴∠BAF=∠ADE.
在△AFB和△DEA中,
∴△AFB≌△DEA(AAS).∴AE=BF.在Rt△ABG中,AB=4,BG=3,根据勾股定理,得AG==5.
∵S△ABG=AB·BG=AG·BF,∴4×3=5BF.∴BF=.∴AE=BF=.∴EG=AG-AE=.
17.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ODE=∠OBF.
∵AE=CF,
∴AD-AE=BC-CF,即DE=BF.
又∵∠DOE=∠BOF,
∴△DOE≌△BOF(AAS).
∴OE=OF.
18.解:(1)证明:∵D是AC的中点,
∴AD=CD.
∵DF=DE,
∴四边形AECF是平行四边形.
∵DE⊥AC,
∴四边形AECF是菱形.
(2)由(1),知四边形AECF是菱形,
∴AE=CE=4.
∵BE=1,CE=4,
∴BC=BE+CE=5.
∴在Rt△ABE中,
AB===.
在Rt△ABC中,
AC===2.
∵S菱形AECF=EF·AC=AB·CE,
即EF·2=×4,
∴EF=2.
19.解:(1)四边形AGCH是菱形.理由如下:
∵四边形ABCD和四边形AFCE是矩形,
∴∠B=∠F=90°,AD∥BC,AF∥CE.
∴四边形AGCH是平行四边形,
∵S AGCH=GC·AB=AG·CF,AB=CF,
∴GC=AG.
∴四边形AGCH是菱形.
(2)由(1)可知,GC=AG,
设GC=AG=x,则BG=8-x.
在Rt△ABG中,AB=4,
由勾股定理,得AB2+BG2=AG2,
即42+(8-x)2=x2.
解得x=5.
∴GC=5.
∴S四边形AGCH=GC·AB=5×4=20.
20.证明:(1)∵AE⊥BN,DF⊥BN,
∴AE∥DF.
∵AD∥EF,
∴四边形AEFD是平行四边形.
∵AE⊥BN,
∴∠AEF=90°.
∴四边形AEFD是矩形.
(2)∵四边形AEFD是矩形,
∴AD=EF.
∵BE=CF,
∴BE+EC=EC+CF,即BC=EF.
∴AD=BC.
∵AD∥BC,
∴四边形ABCD是平行四边形.
∵BD平分∠ABC,
∴∠ABD=∠DBC.
∵AD∥BC,
∴∠ADB=∠DBC.
∴∠ABD=∠ADB.
∴AB=AD.
∴四边形ABCD是菱形.
∴AC⊥BD.
21.解:(1)证明:∵四边形ABCD是菱形,
∴BC∥AD,BC=AD.
∵EF=BC,
∴EF∥AD,且EF=AD.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形.
(2)∵四边形ABCD是菱形,
∴BC=CD.
∵BF=18,
∴CF=18-BC=18-CD.
由(1)知,四边形AEFD是矩形,
∴∠F=90°.
∴DF2+CF2=CD2.
∴62+(18-CD)2=CD2.
解得CD=10.
∴CD的长为10.
22.解:(1)证明:如图,过点O作OH⊥AB于点H.
∵OF⊥AC,OG⊥BC,
∴∠OGC=∠OFC=90°.
∵∠C=90°,
∴四边形OGCF是矩形.
∵AD,BE分别是∠BAC,∠ABC的平分线,OF⊥AC,OG⊥BC,
∴OG=OH=OF.
∴四边形OGCF是正方形.
(2)在Rt△ABC中,
∵∠BAC=60°,
∴∠ABC=90°-∠BAC=90°-60°=30°.
∴AC=AB.
∵AC=4,
∴AB=2AC=2×4=8.
∵AC2+BC2=AB2,
∴BC==4.
在Rt△AOH和Rt△AOF中,
∴Rt△AOH≌Rt△AOF(HL).
∴AH=AF.
同理可得Rt△BOH≌Rt△BOG.
∴BH=BG.
设正方形OGCF的边长为x,
则AH=AF=4-x,BH=BG=4-x.
∴4-x+4-x=8.
∴x=2-2.
∴正方形OGCF的边长为2-2.
23.解:(1)证明:∵四边形ABCD和CEFG均是正方形,
∴AB=AD,EC=EF,∠BAD=∠B=∠ADC=∠ADH=90°.
在△ADH和△ABK中,
∴△ADH≌△ABK(SAS).
∴AK=AH.
(2)证明:由(1)同理可得△HGF≌△KEF≌
△ABK≌△ADH.
∴AH=AK=HF=FK.
∴四边形AKFH是菱形.
∵△ADH≌△ABK,
∴∠HAD=∠BAK.
∵∠BAK+∠DAK=∠BAD=90°,
∴∠HAK=∠HAD+∠DAK=90°.
∴四边形AKFH是正方形.
(3)如图,连接AE.
∵四边形AKFH的面积为10,
由(2)知,四边形AKFH是正方形,
∴KF=.
∵EF=CE=1,
∴KE===3.
∴AB=KE=3.
∵BK=EF=1,
∴BE=BK+KE=4.
∴AE===5.
∴点A,E之间的距离为5.
24.解:(1)证明:∵AD∥BC,
∴∠ADO=∠CBO.
在△ADO和△CBO中,
∴△ADO≌△CBO(AAS).
∴OD=OB.
∴四边形ABCD是平行四边形.
∵AB=BC,
∴四边形ABCD是菱形.
(2)与线段CE相等的线段有AE,DE,AG,CF.
解法提示:由(1)知,四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD.
∵AB=AC,
∴AB=BC=CD=AD=AC.
∴△ABC和△ADC为等边三角形.
∵CH⊥AD,
∴AH=DH,
即CH为AD的垂直平分线.
∴AE=DE.
同理可得CE=AE.
∴AE=DE=EC.
∵△ADC为等边三角形,
∴∠ACD=60°.
又∵CH⊥AD,
∴∠ACH=∠ACD=30°.
∵∠FEC=75°,
∴∠EFC=180°-∠ACH-∠FEC=75°.
∴∠EFC=∠FEC.
∴CF=CE.
∵△ABC和△ADC为等边三角形,
∴∠BAC=∠CAD=60°.
∵CE=AE,
∴∠EAC=∠ECA=30°.
∴∠BAE=∠BAC+∠CAE=90°,∠AEC=180°-∠EAC-∠ECA=120°.
∴∠AEG=∠AEC-∠FEC=45°.
∴△AGE为等腰直角三角形.
∴AE=AG.∴AG=CE.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024沧州盐山县期末)如图,在△ABC中,∠C=90°,AB=13,AC=5,D,E分别是AC,AB的中点,则DE的长是 ( )
A.5 B.6 C.7 D.8
2.如图,在 ABCD中,∠A-∠B=50°,则∠C的度数是 ( )
A.130° B.115° C.65° D.50°
3.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.在此滑动过程中,点P到点O的距离 ( )
A.变小 B.不变 C.变大 D.无法判断
4.如图,若直线m∥n,则下列线段的长可以表示平行线m与n之间的距离的是 ( )
A.AB B.AC C.AD D.DE
5.如图,已知点A的坐标为(-2,2),菱形ABCD的对角线交于坐标原点O,则点C的坐标是 ( )
A.(-2,-2) B.(2,-2) C.(2,-2) D.(-2,-2)
6.已知四边形ABCD是平行四边形,下列说法正确的是 ( )
①当AB=BC时,它是矩形;②当AC⊥BD时,它是菱形;
③当∠ABC=90°时,它是菱形;④当AC=BD时,它是正方形.
A.①② B.② C.②④ D.③④
7.如图,在矩形ABCD中,AB=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E.若BE=EO,则AD的长是 ( )
A.6 B.4 C.8 D.6
8.(2024海南中考)如图,菱形ABCD的边长为2,∠ABC=120°,边AB在数轴上,将AC绕点A顺时针旋转,点C落在数轴上的点E处.若点E表示的数是3,则点A表示的数是 ( )
A.1 B.1- C.0 D.3-2
9.如图,已知正方形ABCD的边长为1,E为边BC上一点,连接AE,作∠DAE的平分线交CD于点F.若F为CD的中点,则BE的长为( )
A. B. C. D.
10.如图,在 ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,图中面积相等的平行四边形有( )
A.2对 B.3对 C.4对 D.5对
11.如图,在 ABCD中,对角线AC,BD相交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点,连接EF,FG,EG,BE.下列结论:①BE⊥AC;②EG=GF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是 ( )
A.①②③ B.①③④ C.①②⑤ D.②③⑤
12.(2024重庆B卷中考)如图,在边长为4的正方形ABCD中,E是BC上一点,F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M,连接EM.若BE=DF=1,则DM的长度为 ( )
A.2 B. C. D.
二、填空题(本大题共4个小题,每小题3分,共12分)
13.如图, ABCD的对角线AC,BD相交于点O,E为AB的中点,AE=3,OE=4,则 ABCD的周长为 .
14.如图,将矩形纸片ABCD沿对角线AC对折,使得点B落在点E处,CE交AD于点F.若CE平分∠ACD,AF=3,则EF的长是 .
15.如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,要使四边形DBCE成为矩形,可添加一个条件是 .(只要写出一个条件即可)
16.如图,正方形ABCD的边长为4,点G在BC上,且BG=3,DE⊥AG于点E,BF∥DE,交AG于点F,则EG的长为 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)如图,在 ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O.
求证:OE=OF.
18.(8分)如图,在Rt△ABC中,∠ABC=90°,AB
(2)若BE=1,CE=4,求EF的长.
19.(8分)将两张长为8、宽为4的矩形纸片按如图所示叠放.
(1)判断四边形AGCH的形状,并说明理由.
(2)求四边形AGCH的面积.
20.(8分)如图,BD平分∠ABF,A是射线BM上一点,过点A作AD∥BN交BG于点D,过点A作AE⊥BN于点E,过点D作DF⊥BN于点F.
(1)求证:四边形AEFD是矩形.
(2)在BF上取点C,使得CF=BE,连接AC,CD.求证:AC⊥BD.
21.(8分)如图,在菱形ABCD中,过点A作AE⊥BC于点E,延长BC至点F,使EF=BC,连接DF.
(1)求证:四边形AEFD是矩形.
(2)若BF=18,DF=6,求CD的长.
22.(8分)如图,在Rt△ABC中,两锐角的平分线AD,BE相交于点O,OF⊥AC于点F,OG⊥BC于点G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
23.(12分)如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.
(1)求证:AK=AH.
(2)求证:四边形AKFH是正方形.
(3)若四边形AKFH的面积为10,CE=1,求点A,E之间的距离.
24.(12分)(2024哈尔滨中考)如图1,四边形ABCD的对角线AC,BD相交于点O,AD∥BC,OA=OC,AB=BC.
(1)求证:四边形ABCD是菱形.
(2)如图2,AB=AC,CH⊥AD于点H,交BD于点E,连接AE,点G在AB上,连接EG交AC于点F.若∠FEC=75°,在不添加任何辅助线的情况下,直接写出四条与线段CE相等的线段(线段CE除外).
图1 图2
【详解答案】
1.B 解析:在△ABC中,∠C=90°,AB=13,AC=5,则BC===12,∵D,E分别是AC,AB的中点,
∴DE=BC=6.故选B.
2.B 解析:∵四边形ABCD是平行四边形,∴∠A=∠C,AD∥BC.∴∠A+∠B=180°.∵∠A-∠B=50°,∴2∠A=230°.∴∠A=115°.∴∠C=115°.故选B.
3.B 解析:如图,连接OP.∵∠AOB=90°,P为AB的中点,∴OP=AB,即在木棍滑动的过程中,点P到点O的距离不发生变化,永远是AB.故选B.
4.B 解析:∵m∥n,AC⊥n,∴AC⊥m.∴AC可以表示平行线m与n之间的距离.故选B.
5.B 解析:∵四边形ABCD为菱形,∴OA=OC,OB=OD.∵点O为坐标原点,∴点A和点C关于原点对称,点B和点D关于原点对称.∵点A的坐标为(-2,2),∴点C的坐标为(2,-2).故选B.
6.B 解析:①若AB=BC,则 ABCD是菱形,选项说法错误;②若AC⊥BD,则 ABCD是菱形,选项说法正确;③若∠ABC=90°,则 ABCD是矩形,选项说法错误;④若AC=BD,则 ABCD是矩形,选项说法错误.综上所述,说法正确的是②.故选B.
7.D 解析:∵四边形ABCD是矩形,∴OA=AC,OB=BD,∠BAD=90°,AC=BD.∴OA=OB.∵AE⊥BD,BE=EO.
∴AE垂直平分OB.∴AB=OA.∴AB=OA=OB=6.∴BD=2OB=12.∴AD==6.故选D.
8.D 解析:如图,过点C作AE的垂线,垂足为F.
∵四边形ABCD是菱形,∴AB=BC=2,AC平分∠DAB,AD∥BC.∴∠DAB+∠ABC=180°.∴∠DAB=180°-∠ABC=
60°.∴∠CAB=∠DAB=30°.∴AC=2CF.∵∠ABC=120°,∴∠CBF=180°-∠ABC=60°.∴∠BCF=90°-∠CBF=30°.∴BF=BC=1.∴在Rt△BCF中,CF===.∴AC=2CF=2.∴AE=AC=2.∵点E表示的数是3,∴点A表示的数是3-2.故选D.
9.C 解析:如图,过点F作FH⊥AE于点H,连接EF.
∵F为CD的中点,
∴DF=CF=.
∵四边形ABCD是正方形,
∴∠D=∠C=∠B=90°.
∵AF是∠DAE的平分线,
∴DF=HF=CF.
∴Rt△ADF≌Rt△AHF(HL).∴AD=AH=1.同理可得Rt△EFH≌Rt△EFC.
∴EH=CE.设CE=EH=x,则AE=1+x,BE=1-x.在Rt△ABE中,AB2+BE2=AE2,∴12+(1-x)2=(1+x)2.解得x=.∴BE=1-=.故选C.
10.B 解析:∵四边形ABCD是平行四边形,∴S△ABD=S△CBD.∵BP是 BEPG的对角线,∴S△BEP=S△BGP.∵PD是 HPFD的对角线,∴S△HPD=S△FPD.∴S△ABD-S△BEP-S△HPD=S△BCD-S△BGP-S△PFD,即S AEPH=S GCFP.∴S ABGH=
S BCFE,同理S AEFD=S GCDH.综上所述,S ABGH=S BCFE,S AEPH=S GCFP,S AEFD=S GCDH,共3对.故选B.
11.B 解析:∵四边形ABCD是平行四边形,∴BO=DO=BD,AD=BC,AB=CD,AB∥CD.又∵BD=2AD,
∴OB=BC=OD=DA.∵E是OC的中点,∴BE⊥AC.故①正确;∵E,F分别是OC,OD的中点,∴EF∥CD,EF=CD.∵G是Rt△ABE斜边AB上的中点,∴GE=AB=AG=BG.∴EG=EF=AG=BG,无法证明EG=GF.故②错误;
∵BG=EF,AB∥CD∥EF,∴四边形BGFE是平行四边形.∴FG=BE.又∵FE=BG,GE=EG,∴△EFG≌△GBE(SSS).故③正确;∵EF∥CD∥AB,∴∠BAC=∠ACD=∠AEF.∵AG=GE,∴∠GAE=∠AEG.∴∠AEG=∠AEF.∴EA平分∠GEF.故④正确;若四边形BEFG是菱形,∴BE=BG=AB.∴∠BAC=30°.与题意不符合,故⑤错误.综上所述,结论正确的是①③④.故选B.
12.D 解析:∵四边形ABCD是正方形,
∴AB=AD,∠ABE=∠ADC=∠ADF=90°.
在Rt△ABE和Rt△ADF中,
∴Rt△ABE≌Rt△ADF(SAS).
∴AE=AF.
∵AM平分∠EAF,
∴∠EAM=∠FAM.
在△AEM和△AFM中,
∴△AEM≌△AFM(SAS).∴EM=FM.
∵四边形ABCD是正方形,
∴BC=CD=4,∠BCD=90°.
设DM=x,则MC=CD-DM=4-x,CE=BC-BE=4-1=3,EM=FM=FD+DM=1+x.
在Rt△MCE中,根据勾股定理,
得EM2=MC2+CE2,
即(1+x)2=(4-x)2+32,
解得x=.故选D.
13.28 解析:∵四边形ABCD是平行四边形,其对角线AC,BD相交于点O,∴AO=CO=AC.∵E为AB的中点,AE=3,∴AB=2AE=6,OE是△ABC的中位线.∴BC=2OE=8.∴ ABCD的周长为2(AB+BC)=2×(6+8)=28.
14. 解析:∵四边形ABCD为矩形,∴∠B=∠D=∠BCD=90°,AB=CD,AD∥BC.∴∠DAC=∠ACB.由折叠可知,AB=AE,∠B=∠E=90°,∠ACB=∠ACE,∴∠CAF=∠ACF.∵AF=3,CE平分∠ACD,∴AF=CF=3,∠ACB=
∠ACF=∠FCD=30°.∴DF=CF=.∵∠B=∠E=90°,AB=AE,∴∠D=∠E=90°,CD=AE.又∵∠CFD=∠AFE,
∴△CDF≌△AEF(AAS).∴EF=DF=.
15.CD=BE(答案不唯一) 解析:∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC.又∵AD=DE,∴DE∥BC,且DE=BC.∴四边形DBCE为平行四边形.添加CD=BE,∴ DBCE为矩形.
16. 解析:∵DE⊥AG,BF∥DE,∴BF⊥AG.∴∠AED=∠BFA=90°.∵四边形ABCD是正方形,∴AB=AD且
∠BAD=∠ADC=90°.∴∠BAF+∠EAD=90°.∵∠EAD+∠ADE=90°,∴∠BAF=∠ADE.
在△AFB和△DEA中,
∴△AFB≌△DEA(AAS).∴AE=BF.在Rt△ABG中,AB=4,BG=3,根据勾股定理,得AG==5.
∵S△ABG=AB·BG=AG·BF,∴4×3=5BF.∴BF=.∴AE=BF=.∴EG=AG-AE=.
17.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ODE=∠OBF.
∵AE=CF,
∴AD-AE=BC-CF,即DE=BF.
又∵∠DOE=∠BOF,
∴△DOE≌△BOF(AAS).
∴OE=OF.
18.解:(1)证明:∵D是AC的中点,
∴AD=CD.
∵DF=DE,
∴四边形AECF是平行四边形.
∵DE⊥AC,
∴四边形AECF是菱形.
(2)由(1),知四边形AECF是菱形,
∴AE=CE=4.
∵BE=1,CE=4,
∴BC=BE+CE=5.
∴在Rt△ABE中,
AB===.
在Rt△ABC中,
AC===2.
∵S菱形AECF=EF·AC=AB·CE,
即EF·2=×4,
∴EF=2.
19.解:(1)四边形AGCH是菱形.理由如下:
∵四边形ABCD和四边形AFCE是矩形,
∴∠B=∠F=90°,AD∥BC,AF∥CE.
∴四边形AGCH是平行四边形,
∵S AGCH=GC·AB=AG·CF,AB=CF,
∴GC=AG.
∴四边形AGCH是菱形.
(2)由(1)可知,GC=AG,
设GC=AG=x,则BG=8-x.
在Rt△ABG中,AB=4,
由勾股定理,得AB2+BG2=AG2,
即42+(8-x)2=x2.
解得x=5.
∴GC=5.
∴S四边形AGCH=GC·AB=5×4=20.
20.证明:(1)∵AE⊥BN,DF⊥BN,
∴AE∥DF.
∵AD∥EF,
∴四边形AEFD是平行四边形.
∵AE⊥BN,
∴∠AEF=90°.
∴四边形AEFD是矩形.
(2)∵四边形AEFD是矩形,
∴AD=EF.
∵BE=CF,
∴BE+EC=EC+CF,即BC=EF.
∴AD=BC.
∵AD∥BC,
∴四边形ABCD是平行四边形.
∵BD平分∠ABC,
∴∠ABD=∠DBC.
∵AD∥BC,
∴∠ADB=∠DBC.
∴∠ABD=∠ADB.
∴AB=AD.
∴四边形ABCD是菱形.
∴AC⊥BD.
21.解:(1)证明:∵四边形ABCD是菱形,
∴BC∥AD,BC=AD.
∵EF=BC,
∴EF∥AD,且EF=AD.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形.
(2)∵四边形ABCD是菱形,
∴BC=CD.
∵BF=18,
∴CF=18-BC=18-CD.
由(1)知,四边形AEFD是矩形,
∴∠F=90°.
∴DF2+CF2=CD2.
∴62+(18-CD)2=CD2.
解得CD=10.
∴CD的长为10.
22.解:(1)证明:如图,过点O作OH⊥AB于点H.
∵OF⊥AC,OG⊥BC,
∴∠OGC=∠OFC=90°.
∵∠C=90°,
∴四边形OGCF是矩形.
∵AD,BE分别是∠BAC,∠ABC的平分线,OF⊥AC,OG⊥BC,
∴OG=OH=OF.
∴四边形OGCF是正方形.
(2)在Rt△ABC中,
∵∠BAC=60°,
∴∠ABC=90°-∠BAC=90°-60°=30°.
∴AC=AB.
∵AC=4,
∴AB=2AC=2×4=8.
∵AC2+BC2=AB2,
∴BC==4.
在Rt△AOH和Rt△AOF中,
∴Rt△AOH≌Rt△AOF(HL).
∴AH=AF.
同理可得Rt△BOH≌Rt△BOG.
∴BH=BG.
设正方形OGCF的边长为x,
则AH=AF=4-x,BH=BG=4-x.
∴4-x+4-x=8.
∴x=2-2.
∴正方形OGCF的边长为2-2.
23.解:(1)证明:∵四边形ABCD和CEFG均是正方形,
∴AB=AD,EC=EF,∠BAD=∠B=∠ADC=∠ADH=90°.
在△ADH和△ABK中,
∴△ADH≌△ABK(SAS).
∴AK=AH.
(2)证明:由(1)同理可得△HGF≌△KEF≌
△ABK≌△ADH.
∴AH=AK=HF=FK.
∴四边形AKFH是菱形.
∵△ADH≌△ABK,
∴∠HAD=∠BAK.
∵∠BAK+∠DAK=∠BAD=90°,
∴∠HAK=∠HAD+∠DAK=90°.
∴四边形AKFH是正方形.
(3)如图,连接AE.
∵四边形AKFH的面积为10,
由(2)知,四边形AKFH是正方形,
∴KF=.
∵EF=CE=1,
∴KE===3.
∴AB=KE=3.
∵BK=EF=1,
∴BE=BK+KE=4.
∴AE===5.
∴点A,E之间的距离为5.
24.解:(1)证明:∵AD∥BC,
∴∠ADO=∠CBO.
在△ADO和△CBO中,
∴△ADO≌△CBO(AAS).
∴OD=OB.
∴四边形ABCD是平行四边形.
∵AB=BC,
∴四边形ABCD是菱形.
(2)与线段CE相等的线段有AE,DE,AG,CF.
解法提示:由(1)知,四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD.
∵AB=AC,
∴AB=BC=CD=AD=AC.
∴△ABC和△ADC为等边三角形.
∵CH⊥AD,
∴AH=DH,
即CH为AD的垂直平分线.
∴AE=DE.
同理可得CE=AE.
∴AE=DE=EC.
∵△ADC为等边三角形,
∴∠ACD=60°.
又∵CH⊥AD,
∴∠ACH=∠ACD=30°.
∵∠FEC=75°,
∴∠EFC=180°-∠ACH-∠FEC=75°.
∴∠EFC=∠FEC.
∴CF=CE.
∵△ABC和△ADC为等边三角形,
∴∠BAC=∠CAD=60°.
∵CE=AE,
∴∠EAC=∠ECA=30°.
∴∠BAE=∠BAC+∠CAE=90°,∠AEC=180°-∠EAC-∠ECA=120°.
∴∠AEG=∠AEC-∠FEC=45°.
∴△AGE为等腰直角三角形.
∴AE=AG.∴AG=CE.
