第十六章 二次根式 评估测试卷(含答案)2024-2025学年数学人教版八年级下册
文档属性
| 名称 | 第十六章 二次根式 评估测试卷(含答案)2024-2025学年数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 76.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:21:05 | ||
图片预览


文档简介
第十六章 二次根式评估测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024绥化中考)若式子有意义,则m的取值范围是 ( )
A.m≤ B.m≥- C.m≥ D.m≤-
2.(2024济宁中考)下列计算正确的是 ( )
A.+= B.×=
C.2÷=1 D.=-5
3.若=·,则x的取值范围是 ( )
A.x≥6 B.x≥0
C.0≤x≤6 D.x为一切实数
4.在二次根式,,,,中,最简二次根式有 ( )
A.1个 B.2个 C.3个 D.4个
5.下列等式不成立的是 ( )
A.÷=2 B.×=6
C.=2 D.=
6.下列各式中,不能与合并的是 ( )
A. B. C. D.
7.下列各式计算正确的是 ( )
A.6-2=4 B.5+2=5
C.2×3=6 D.6÷3=2
8.(2024张家口万全区期末)已知a=4+2,b=4-2,则a2b-ab2的值为 ( )
A.-32 B.32
C.-16 D.16
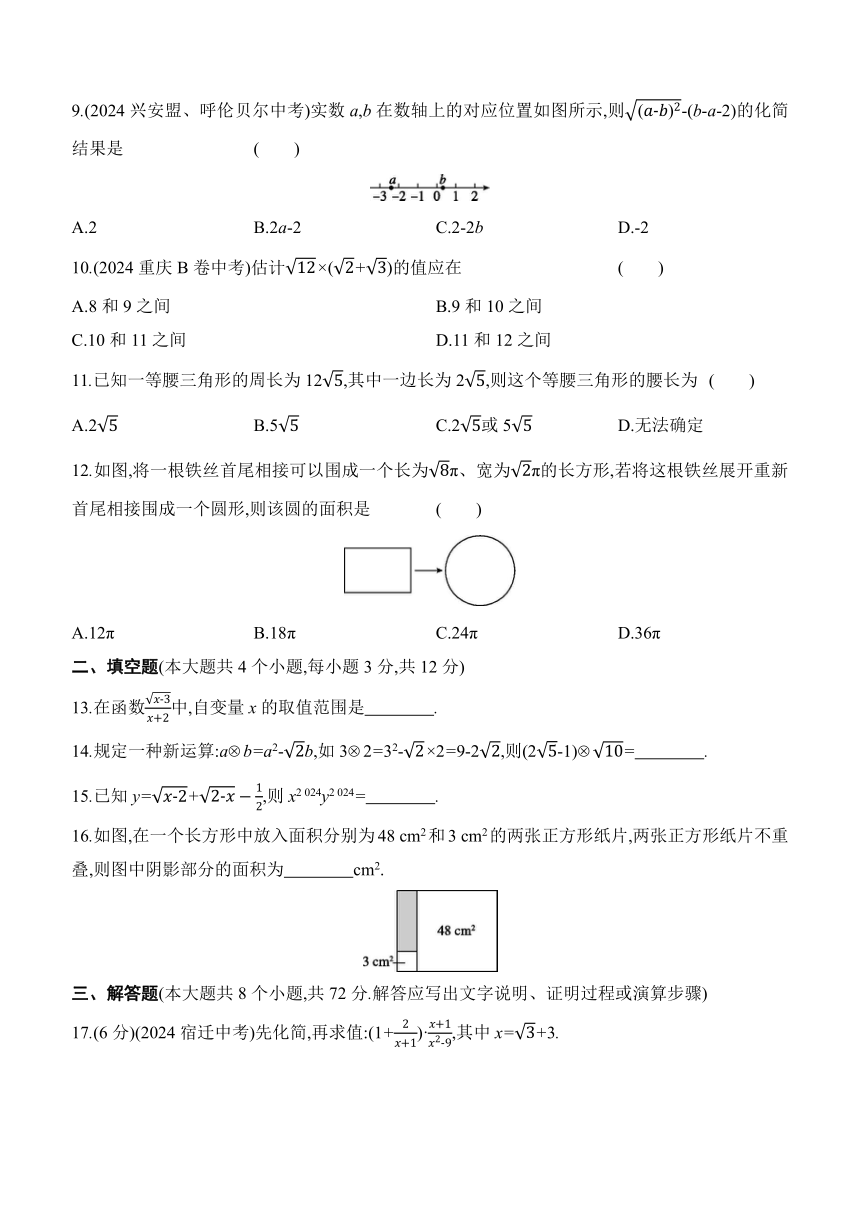
9.(2024兴安盟、呼伦贝尔中考)实数a,b在数轴上的对应位置如图所示,则-(b-a-2)的化简结果是 ( )
A.2 B.2a-2 C.2-2b D.-2
10.(2024重庆B卷中考)估计×(+)的值应在 ( )
A.8和9之间 B.9和10之间
C.10和11之间 D.11和12之间
11.已知一等腰三角形的周长为12,其中一边长为2,则这个等腰三角形的腰长为 ( )
A.2 B.5 C.2或5 D.无法确定
12.如图,将一根铁丝首尾相接可以围成一个长为π、宽为π的长方形,若将这根铁丝展开重新首尾相接围成一个圆形,则该圆的面积是 ( )
A.12π B.18π C.24π D.36π
二、填空题(本大题共4个小题,每小题3分,共12分)
13.在函数中,自变量x的取值范围是 .
14.规定一种新运算:a b=a2-b,如3 2=32-×2=9-2,则(2-1) = .
15.已知y=+,则x2 024y2 024= .
16.如图,在一个长方形中放入面积分别为48 cm2和3 cm2的两张正方形纸片,两张正方形纸片不重叠,则图中阴影部分的面积为 cm2.
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)(2024宿迁中考)先化简,再求值:(1+)·,其中x=+3.
18.(8分)下面是小文同学进行二次根式混合运算的过程,请认真阅读,完成相应的任务:
解:()2×(5+2) =(3-2+2)×(5+2) 第1步 =(5-2)×(5+2) 第2步 =25-12 第3步 =13. 第4步
任务:
(1)上述解答过程中,第1步依据的乘法公式为 (用字母表示).
(2)上述解答过程,从第 步开始出错.
(3)请写出正确的计算过程.
19.(6分)在一个长为5 cm、宽为4 cm的长方体塑料容器中装满水,然后将这个塑料容器内的一部分水倒入一个高为 cm的圆柱形玻璃容器中,当玻璃容器装满水时,塑料容器中的水面下降了 cm.求圆柱形玻璃容器的底面半径.
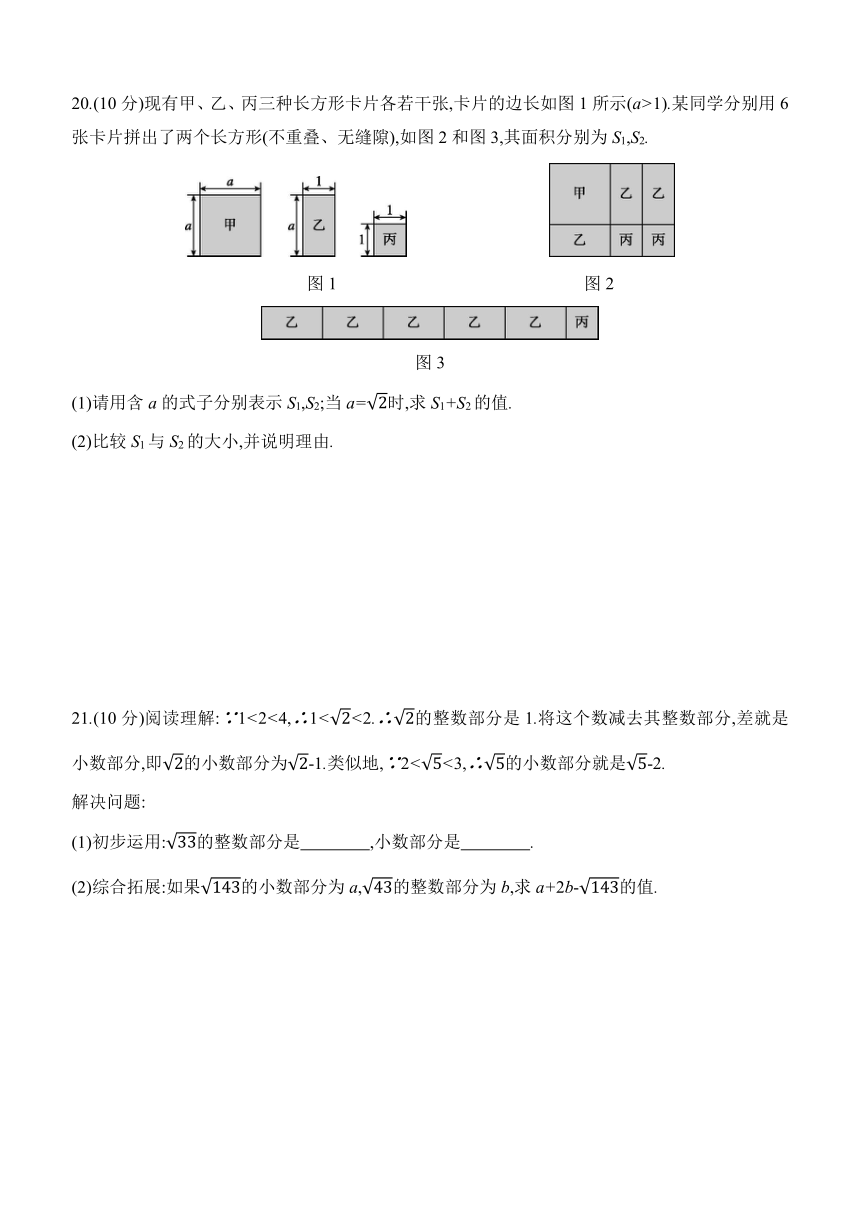
20.(10分)现有甲、乙、丙三种长方形卡片各若干张,卡片的边长如图1所示(a>1).某同学分别用6张卡片拼出了两个长方形(不重叠、无缝隙),如图2和图3,其面积分别为S1,S2.
图1 图2
图3
(1)请用含a的式子分别表示S1,S2;当a=时,求S1+S2的值.
(2)比较S1与S2的大小,并说明理由.
21.(10分)阅读理解:∵1<2<4,∴1<<2.∴的整数部分是1.将这个数减去其整数部分,差就是小数部分,即的小数部分为-1.类似地,∵2<<3,∴的小数部分就是-2.
解决问题:
(1)初步运用:的整数部分是 ,小数部分是 .
(2)综合拓展:如果的小数部分为a,的整数部分为b,求a+2b-的值.
22.(10分)如图,某校有一块形状为正方形的绿地,其边长为(+2)m,现在要在正方形绿地内修建四个大小、形状相同的长方形花坛,每个花坛的长为(+1)m、宽为(-1)m,除去修建花坛的地方,其他地方全部修建成通道.
(1)求通道的总面积.
(2)若要在通道上铺设造价为8元/m2的地砖,如果要铺完整个通道,那么购买地砖需要花费多少元 (参考数据:≈1.41)
23.(10分)定义:若两个二次根式a,b满足a·b=c,且c为有理数,则称a与b是关于c的共轭二次根式.
(1)与是关于 的共轭二次根式.
(2)若m与2-3是关于2的共轭二次根式,则m= .
(3)若3+与6+n是关于12的共轭二次根式,求n的值.
24.(12分)阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2=(1+)2,善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a,b,m,n均为正整数),则有
a+b=m2+2n2+2mn.
∴a=m2+2n2,b=2mn.
这样小明就找到了一种把部分a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a,b,m,n均为正整数时,若a+b=(m+n)2,用含m,n的式子分别表示a,b,得a= ,b= .
(2)利用所探索的结论,找一组正整数a,b,m,n,填空:
+ =( + )2.
(3)若a+4=(m+n)2,且a,m,n均为正整数,求a的值.
【详解答案】
1.C 解析:由题意,得2m-3≥0.解得m≥.故选C.
2.B 解析:A.与不能合并,故A选项错误;B.=,故B选项正确;C.2÷==,故C选项错误;D.=|-5|=5,故D选项错误.故选B.
3.A 解析:根据题意,得x≥0且x-6≥0.解得x≥6.故选A.
4.A 解析:∵=,=4,是最简二次根式,=,=|x|,∴最简二次根式有1个.故选A.
5.D 解析:A.==2,故此选项不符合题意;B.==6,故此选项不符合题意;C.==2,故此选项不符合题意;D.==,故此选项符合题意.故选D.
6.D 解析:=,A.=2,能与合并,故A不符合题意;B.=
,能与合并,故B不符合题意;C.=5,能与合并,故C不符合题意;D.=,不能与合并,故D符合题意.故选D.
7.C 解析:A.6-2=4,原计算错误,不符合题意;B.5与2不能合并,原计算错误,不符合题意;C.2×3=6,原计算正确,符合题意;D.6÷3=2,原计算错误,不符合题意.故选C.
8.C 解析:∵a=4+2,b=4-2,∴a2b-ab2=ab(a-b)=(4+2)(4-2)·(4+2-4+2)=(16-20)×4=-16.故选C.
9.A 解析:由数轴可知,-310.C 解析:∵×(+)=2+6,而4<2=<5,∴10<2+6<11.故选C.
11.B 解析:由题意知,有以下两种情况:①当腰长为2时,则底边长为12-2×2=8,
∵2+2=4<8,∴此时不能构成三角形,舍去.②当底边长为2时,则腰长为=5.
∵5+5=10>2,∴此时能构成三角形.∴这个等腰三角形的腰长为5.故选B.
12.B 解析:这根铁丝的周长为2(π+π)=6π.∴将这根铁丝展开重新首尾相接围成一个圆形,则该圆的半径为=3.∴该圆的面积为(3)2π=18π.故选B.
13.x≥3 解析:根据题意,得x-3≥0,且x+2≠0.解得x≥3.
14.21-6 解析:∵a b=a2-b,
∴(2-1) =(2-1)2-=20-4+1-2=21-6.
15.1 解析:由题意,得解得x=2.∴y=+-=-.
∴x2 024y2 024=(xy)2 024=(-×2)2 024=(-1)2 024=1.
16.9 解析:依题意,得两个正方形纸片的边长分别为=4(cm)和 cm,则阴影部分的面积为(4-)×=3=9(cm2).
17.解:(1+)·=·=·=.
当x=+3时,
原式===.
18.解:(1)(a-b)2=a2-2ab+b2
(2)3
(3)(-)2×(5+2)
=(3-2+2)×(5+2)
=(5-2)×(5+2)
=25-24
=1.
19.解:从塑料容器中倒出的水的体积为
5×4=120(cm3).
设圆柱形玻璃容器的底面半径为r cm.
由题意,得πr2=120.
解得r=.
答:圆柱形玻璃容器的底面半径为 cm.
20.解:(1)依题意,得S甲=a2,S乙=a,S丙=1.
∴S1=S甲+3S乙+2S丙=a2+3a+2,S2=5S乙+S丙=5a+1.
∴S1+S2=(a2+3a+2)+(5a+1)=a2+8a+3.
当a=时,S1+S2=()2+8×+3=5+8.
(2)S1>S2.理由如下:
∵S1=a2+3a+2,S2=5a+1,
∴S1-S2=(a2+3a+2)-(5a+1)=a2-2a+1=(a-1)2.
∵a>1,∴S1-S2=(a-1)2>0.
∴S1>S2.
21.解:(1)5 -5
(2)∵121<143<144,
∴11<<12.
∴的整数部分是11,小数部分是-11,即a=-11.
∵36<43<49,
∴6<<7.
∴的整数部分是6,即b=6.
∴a+2b-=-11+2×6-=1.
22.解:(1)由题意,得通道的总面积为
(+2)2-4(+1)(-1)=50+4+4-4×6=(30+20)(m2).
(2)由(1)可知,通道的总面积为(30+20)m2,
∴购买地砖需要花费8×(30+20)=240+160≈240+160×1.41=465.6(元).
答:购买地砖需要花费465.6元.
23.解:(1)1
(2)2+3
(3)∵3+与6+n是关于12的共轭二次根式,
∴(3+)(6+n)=12.
∴6+n===
2(3-)=6-2.
∴n=6-2-6=-2.
∴n=-2.
24.解:(1)m2+3n2 2mn
(2)(答案不唯一)16 8 2 2
(3)由(1)得4=2mn,∴mn=2,∵a,m,n均为正整数,∴mn=1×2或mn=2×1,
即m=1,n=2或m=2,n=1.
当m=1,n=2时,
a=m2+3n2=12+3×22=13;
当m=2,n=1时,
a=m2+3n2=22+3×12=7.
∴a=13或7.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024绥化中考)若式子有意义,则m的取值范围是 ( )
A.m≤ B.m≥- C.m≥ D.m≤-
2.(2024济宁中考)下列计算正确的是 ( )
A.+= B.×=
C.2÷=1 D.=-5
3.若=·,则x的取值范围是 ( )
A.x≥6 B.x≥0
C.0≤x≤6 D.x为一切实数
4.在二次根式,,,,中,最简二次根式有 ( )
A.1个 B.2个 C.3个 D.4个
5.下列等式不成立的是 ( )
A.÷=2 B.×=6
C.=2 D.=
6.下列各式中,不能与合并的是 ( )
A. B. C. D.
7.下列各式计算正确的是 ( )
A.6-2=4 B.5+2=5
C.2×3=6 D.6÷3=2
8.(2024张家口万全区期末)已知a=4+2,b=4-2,则a2b-ab2的值为 ( )
A.-32 B.32
C.-16 D.16
9.(2024兴安盟、呼伦贝尔中考)实数a,b在数轴上的对应位置如图所示,则-(b-a-2)的化简结果是 ( )
A.2 B.2a-2 C.2-2b D.-2
10.(2024重庆B卷中考)估计×(+)的值应在 ( )
A.8和9之间 B.9和10之间
C.10和11之间 D.11和12之间
11.已知一等腰三角形的周长为12,其中一边长为2,则这个等腰三角形的腰长为 ( )
A.2 B.5 C.2或5 D.无法确定
12.如图,将一根铁丝首尾相接可以围成一个长为π、宽为π的长方形,若将这根铁丝展开重新首尾相接围成一个圆形,则该圆的面积是 ( )
A.12π B.18π C.24π D.36π
二、填空题(本大题共4个小题,每小题3分,共12分)
13.在函数中,自变量x的取值范围是 .
14.规定一种新运算:a b=a2-b,如3 2=32-×2=9-2,则(2-1) = .
15.已知y=+,则x2 024y2 024= .
16.如图,在一个长方形中放入面积分别为48 cm2和3 cm2的两张正方形纸片,两张正方形纸片不重叠,则图中阴影部分的面积为 cm2.
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)(2024宿迁中考)先化简,再求值:(1+)·,其中x=+3.
18.(8分)下面是小文同学进行二次根式混合运算的过程,请认真阅读,完成相应的任务:
解:()2×(5+2) =(3-2+2)×(5+2) 第1步 =(5-2)×(5+2) 第2步 =25-12 第3步 =13. 第4步
任务:
(1)上述解答过程中,第1步依据的乘法公式为 (用字母表示).
(2)上述解答过程,从第 步开始出错.
(3)请写出正确的计算过程.
19.(6分)在一个长为5 cm、宽为4 cm的长方体塑料容器中装满水,然后将这个塑料容器内的一部分水倒入一个高为 cm的圆柱形玻璃容器中,当玻璃容器装满水时,塑料容器中的水面下降了 cm.求圆柱形玻璃容器的底面半径.
20.(10分)现有甲、乙、丙三种长方形卡片各若干张,卡片的边长如图1所示(a>1).某同学分别用6张卡片拼出了两个长方形(不重叠、无缝隙),如图2和图3,其面积分别为S1,S2.
图1 图2
图3
(1)请用含a的式子分别表示S1,S2;当a=时,求S1+S2的值.
(2)比较S1与S2的大小,并说明理由.
21.(10分)阅读理解:∵1<2<4,∴1<<2.∴的整数部分是1.将这个数减去其整数部分,差就是小数部分,即的小数部分为-1.类似地,∵2<<3,∴的小数部分就是-2.
解决问题:
(1)初步运用:的整数部分是 ,小数部分是 .
(2)综合拓展:如果的小数部分为a,的整数部分为b,求a+2b-的值.
22.(10分)如图,某校有一块形状为正方形的绿地,其边长为(+2)m,现在要在正方形绿地内修建四个大小、形状相同的长方形花坛,每个花坛的长为(+1)m、宽为(-1)m,除去修建花坛的地方,其他地方全部修建成通道.
(1)求通道的总面积.
(2)若要在通道上铺设造价为8元/m2的地砖,如果要铺完整个通道,那么购买地砖需要花费多少元 (参考数据:≈1.41)
23.(10分)定义:若两个二次根式a,b满足a·b=c,且c为有理数,则称a与b是关于c的共轭二次根式.
(1)与是关于 的共轭二次根式.
(2)若m与2-3是关于2的共轭二次根式,则m= .
(3)若3+与6+n是关于12的共轭二次根式,求n的值.
24.(12分)阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2=(1+)2,善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a,b,m,n均为正整数),则有
a+b=m2+2n2+2mn.
∴a=m2+2n2,b=2mn.
这样小明就找到了一种把部分a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a,b,m,n均为正整数时,若a+b=(m+n)2,用含m,n的式子分别表示a,b,得a= ,b= .
(2)利用所探索的结论,找一组正整数a,b,m,n,填空:
+ =( + )2.
(3)若a+4=(m+n)2,且a,m,n均为正整数,求a的值.
【详解答案】
1.C 解析:由题意,得2m-3≥0.解得m≥.故选C.
2.B 解析:A.与不能合并,故A选项错误;B.=,故B选项正确;C.2÷==,故C选项错误;D.=|-5|=5,故D选项错误.故选B.
3.A 解析:根据题意,得x≥0且x-6≥0.解得x≥6.故选A.
4.A 解析:∵=,=4,是最简二次根式,=,=|x|,∴最简二次根式有1个.故选A.
5.D 解析:A.==2,故此选项不符合题意;B.==6,故此选项不符合题意;C.==2,故此选项不符合题意;D.==,故此选项符合题意.故选D.
6.D 解析:=,A.=2,能与合并,故A不符合题意;B.=
,能与合并,故B不符合题意;C.=5,能与合并,故C不符合题意;D.=,不能与合并,故D符合题意.故选D.
7.C 解析:A.6-2=4,原计算错误,不符合题意;B.5与2不能合并,原计算错误,不符合题意;C.2×3=6,原计算正确,符合题意;D.6÷3=2,原计算错误,不符合题意.故选C.
8.C 解析:∵a=4+2,b=4-2,∴a2b-ab2=ab(a-b)=(4+2)(4-2)·(4+2-4+2)=(16-20)×4=-16.故选C.
9.A 解析:由数轴可知,-3
11.B 解析:由题意知,有以下两种情况:①当腰长为2时,则底边长为12-2×2=8,
∵2+2=4<8,∴此时不能构成三角形,舍去.②当底边长为2时,则腰长为=5.
∵5+5=10>2,∴此时能构成三角形.∴这个等腰三角形的腰长为5.故选B.
12.B 解析:这根铁丝的周长为2(π+π)=6π.∴将这根铁丝展开重新首尾相接围成一个圆形,则该圆的半径为=3.∴该圆的面积为(3)2π=18π.故选B.
13.x≥3 解析:根据题意,得x-3≥0,且x+2≠0.解得x≥3.
14.21-6 解析:∵a b=a2-b,
∴(2-1) =(2-1)2-=20-4+1-2=21-6.
15.1 解析:由题意,得解得x=2.∴y=+-=-.
∴x2 024y2 024=(xy)2 024=(-×2)2 024=(-1)2 024=1.
16.9 解析:依题意,得两个正方形纸片的边长分别为=4(cm)和 cm,则阴影部分的面积为(4-)×=3=9(cm2).
17.解:(1+)·=·=·=.
当x=+3时,
原式===.
18.解:(1)(a-b)2=a2-2ab+b2
(2)3
(3)(-)2×(5+2)
=(3-2+2)×(5+2)
=(5-2)×(5+2)
=25-24
=1.
19.解:从塑料容器中倒出的水的体积为
5×4=120(cm3).
设圆柱形玻璃容器的底面半径为r cm.
由题意,得πr2=120.
解得r=.
答:圆柱形玻璃容器的底面半径为 cm.
20.解:(1)依题意,得S甲=a2,S乙=a,S丙=1.
∴S1=S甲+3S乙+2S丙=a2+3a+2,S2=5S乙+S丙=5a+1.
∴S1+S2=(a2+3a+2)+(5a+1)=a2+8a+3.
当a=时,S1+S2=()2+8×+3=5+8.
(2)S1>S2.理由如下:
∵S1=a2+3a+2,S2=5a+1,
∴S1-S2=(a2+3a+2)-(5a+1)=a2-2a+1=(a-1)2.
∵a>1,∴S1-S2=(a-1)2>0.
∴S1>S2.
21.解:(1)5 -5
(2)∵121<143<144,
∴11<<12.
∴的整数部分是11,小数部分是-11,即a=-11.
∵36<43<49,
∴6<<7.
∴的整数部分是6,即b=6.
∴a+2b-=-11+2×6-=1.
22.解:(1)由题意,得通道的总面积为
(+2)2-4(+1)(-1)=50+4+4-4×6=(30+20)(m2).
(2)由(1)可知,通道的总面积为(30+20)m2,
∴购买地砖需要花费8×(30+20)=240+160≈240+160×1.41=465.6(元).
答:购买地砖需要花费465.6元.
23.解:(1)1
(2)2+3
(3)∵3+与6+n是关于12的共轭二次根式,
∴(3+)(6+n)=12.
∴6+n===
2(3-)=6-2.
∴n=6-2-6=-2.
∴n=-2.
24.解:(1)m2+3n2 2mn
(2)(答案不唯一)16 8 2 2
(3)由(1)得4=2mn,∴mn=2,∵a,m,n均为正整数,∴mn=1×2或mn=2×1,
即m=1,n=2或m=2,n=1.
当m=1,n=2时,
a=m2+3n2=12+3×22=13;
当m=2,n=1时,
a=m2+3n2=22+3×12=7.
∴a=13或7.
