22.3 三角形的中位线 同步练(含答案)2024-2025学年数学冀教版八年级下册
文档属性
| 名称 | 22.3 三角形的中位线 同步练(含答案)2024-2025学年数学冀教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 253.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 00:00:00 | ||
图片预览


文档简介
22.3三角形的中位线
三角形的中位线
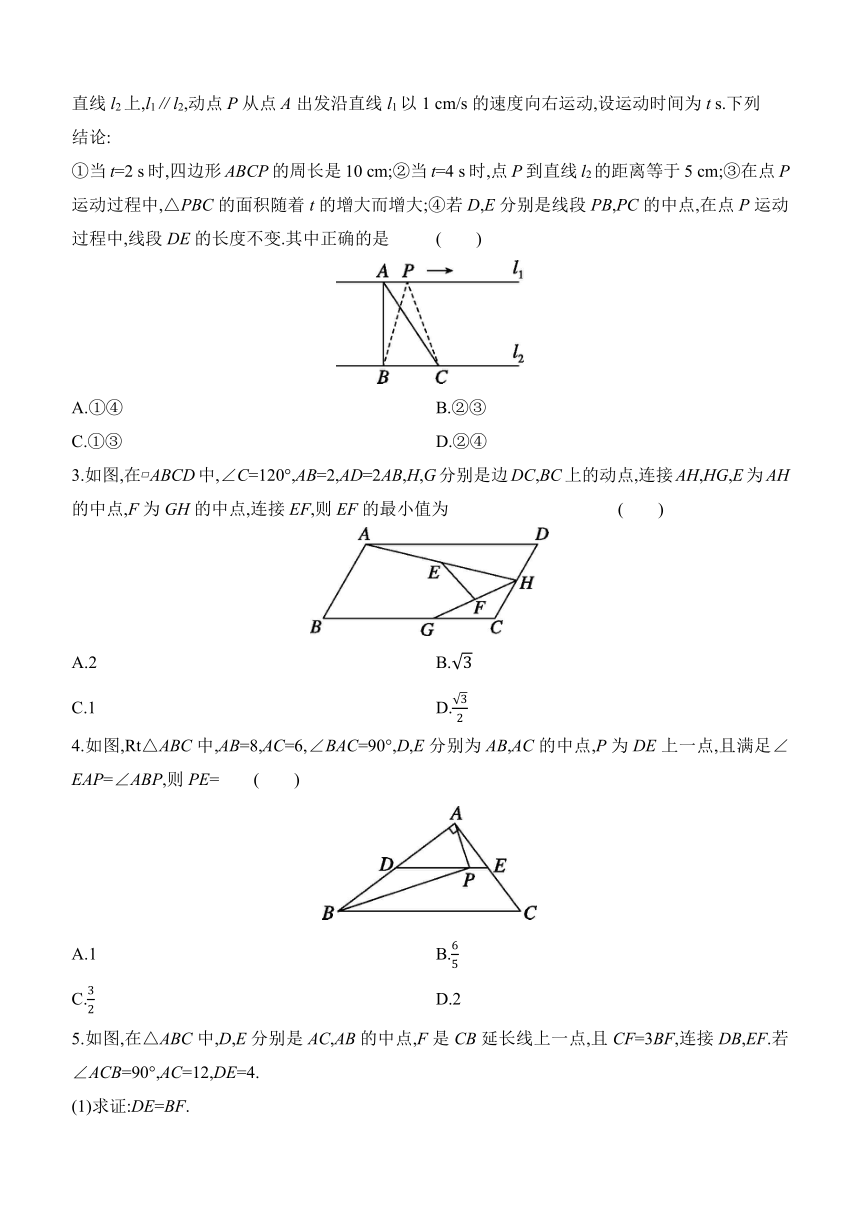
1.(2024兰州中考)如图,小张想估测被池塘隔开的A,B两处景观之间的距离,他先在AB外取一点C,然后步测出AC,BC的中点D,E,并步测出DE的长约为18 m,由此估测A,B之间的距离约为 ( )
A.18 m B.24 m
C.36 m D.54 m
2.(2024广安中考)如图,在△ABC中,D,E分别是AC,BC的中点,若∠A=45°,∠CED=70°,则∠C的度数为 ( )
A.45° B.50° C.60° D.65°
3.已知三角形三条中位线的长分别为3 cm,4 cm,5 cm,则这个三角形的面积为 ( )
A.12 cm2 B.24 cm2
C.36 cm2 D.48 cm2
4.(2024海南中考)如图是跷跷板示意图,支柱OM经过AB的中点O,OM与地面CD垂直于点M,OM=40 cm,当跷跷板的一端A着地时,另一端B离地面的高度为 cm.
5.如图,在△ABC中,AB=4,BC=6,AC=8,D,E,F分别是AB,BC,AC的中点,则△DEF的周长为 .
6.如图,在△ABC中,D,E分别是边AC,AB的中点,连接ED,BD.已知BD平分∠ABC.
求证:BD⊥AC.
7.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3.
(1)求证:BN=DN.
(2)求△ABC的周长.
1.如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是AB,BD,CD,AC的中点,则四边形EFGH的周长为 ( )
A.12 B.14 C.24 D.21
2.(2024宁夏中考)如图,在Rt△ABC中,∠ABC=90°,AB=3 cm,BC=2 cm,点A在直线l1上,点B,C在直线l2上,l1∥l2,动点P从点A出发沿直线l1以1 cm/s的速度向右运动,设运动时间为t s.下列
结论:
①当t=2 s时,四边形ABCP的周长是10 cm;②当t=4 s时,点P到直线l2的距离等于5 cm;③在点P运动过程中,△PBC的面积随着t的增大而增大;④若D,E分别是线段PB,PC的中点,在点P运动过程中,线段DE的长度不变.其中正确的是 ( )
A.①④ B.②③
C.①③ D.②④
3.如图,在 ABCD中,∠C=120°,AB=2,AD=2AB,H,G分别是边DC,BC上的动点,连接AH,HG,E为AH的中点,F为GH的中点,连接EF,则EF的最小值为 ( )
A.2 B.
C.1 D.
4.如图,Rt△ABC中,AB=8,AC=6,∠BAC=90°,D,E分别为AB,AC的中点,P为DE上一点,且满足∠EAP=∠ABP,则PE= ( )
A.1 B.
C. D.2
5.如图,在△ABC中,D,E分别是AC,AB的中点,F是CB延长线上一点,且CF=3BF,连接DB,EF.若∠ACB=90°,AC=12,DE=4.
(1)求证:DE=BF.
(2)求四边形DEFB的周长.
6.(推理能力)如图, 在四边形ABCD中, 对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点 .连接PQ,MN,BD与MN相交于点E,AC与MN相交于点F.
(1) 求证:PQ⊥MN.
(2) 判断△OEF的形状,并说明理由.
【详解答案】
课堂达标
1.C 2.D 3.B 4.80 5.9
6.证明:∵D,E分别是AC,AB的中点,
∴DE是△ABC的中位线,AB=2BE.
∴DE∥BC,BC=2DE.
∴∠CBD=∠EDB.
∵BD平分∠ABC,
∴∠CBD=∠EBD.
∴∠EBD=∠EDB.
∴DE=BE.
∵AB=2BE,∴AB=2DE.
∴AB=BC.
∵D是AC的中点,∴BD⊥AC.
7.(1)证明:∵AN平分∠BAC,
∴∠1=∠2.
∵BN⊥AN,
∴∠ANB=∠AND=90°.
又∵AN=AN,
∴△ABN≌△ADN(ASA).
∴BN=DN.
(2)解:由△ABN≌△ADN,知
AD=AB=10,BN=DN,
∴N为BD的中点.
又∵M是BC的中点,
∴MN为△BCD的中位线.
∴CD=2MN=6.
∴AC=AD+CD=16.
∴△ABC的周长=AB+BC+AC=10+15+16=41.
课后提升
1.A 解析:∵BD⊥CD,BD=4,CD=3,∴BC==5.∵E,F,G,H分别是AB,BD,CD,AC的中点,∴EH=FG=BC,EF=GH=AD.∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC.又∵AD=7,∴四边形EFGH的周长=7+5=12.故选A.
2.A 解析:①当t=2 s时,AP=2 cm,则AP=BC.又因为AP∥BC,所以四边形ABCP是平行四边形.所以PC=AB=
3 cm.所以四边形ABCP的周长为2×(2+3)=10(cm),故①正确.因为平行线间的距离处处相等, AB=3 cm,∠ABC
=90°,所以直线l1与直线l2之间的距离是3 cm.所以当t=4 s时,点P到直线l2的距离仍然是3 cm,故②错误.由上述过程可知,点P到BC的距离为定值3 cm,即△PBC的BC边上的高为3 cm,又因为BC=2 cm,所以△PBC的面积为定值,故③错误.因为D,E分别是线段PB,PC的中点,所以DE是△PBC的中位线,所以DE=BC=1 cm,即线段DE的长度不变,故④正确.故选A.
3.D 解析:如图,连接AG.∵四边形ABCD是平行四边形,∴AB∥CD.∴∠B+∠C=180°.∴∠B=180°-120°=60°.
∵E,F分别是AH,GH的中点,∴EF是△AGH的中位线.∴EF=AG.当AG最小时,EF有最小值,当AG⊥BC时,AG最小,则∠BAG=30°,此时BG=AB=1,AG=BG=.∴EF=AG=,即EF的最小值是.故选D.
4.A 解析:在Rt△ABC中,AB=8,AC=6,由勾股定理,得BC==10.∵D,E分别为AB,AC的中点,∴DE=BC=5.∵∠BAC=90°,∴∠BAP+
∠EAP=90°.∵∠EAP=∠ABP,∴∠BAP+∠ABP=90°.∴∠APB=90°.∵D为AB的中点,∴PD=AB=4.∴PE=DE-DP=1.故选A.
5.(1)证明:∵D,E分别是AC,AB的中点,
∴DE为△ABC的中位线.
∴DE∥BC,DE=BC.
∵CF=3BF,
∴BF=BC.
∴DE=BF.
(2)解:∵D是AC的中点,
AC=12,∴CD=6.
∵DE=4,∴BC=8.
由勾股定理,得
DB==10.
∵DE=BF,DE∥BC,
∴四边形DEFB为平行四边形.
∴四边形DEFB的周长=2×(4+10)=28.
6.(1)证明:如图,连接MP,NP.
∵M,P,N分别是边AB,BC,CD的中点,
∴AM=BM,BP=CP,DN=CN.
∴PM=AC,PN=BD.
又∵AC=BD,∴PM=PN.
∴P在MN的中垂线上.
∵Q是MN的中点,∴PQ⊥MN.
(2)解:△OEF是等腰三角形.
理由如下:∵PM∥AC,
∴∠PMN=∠EFO.
∵PN∥BD,∴∠OEF=∠PNM.
又∵PM=PN,∴∠PMN=∠PNM,
∴∠EFO=∠OEF.
∴△OEF是等腰三角形 .
三角形的中位线
1.(2024兰州中考)如图,小张想估测被池塘隔开的A,B两处景观之间的距离,他先在AB外取一点C,然后步测出AC,BC的中点D,E,并步测出DE的长约为18 m,由此估测A,B之间的距离约为 ( )
A.18 m B.24 m
C.36 m D.54 m
2.(2024广安中考)如图,在△ABC中,D,E分别是AC,BC的中点,若∠A=45°,∠CED=70°,则∠C的度数为 ( )
A.45° B.50° C.60° D.65°
3.已知三角形三条中位线的长分别为3 cm,4 cm,5 cm,则这个三角形的面积为 ( )
A.12 cm2 B.24 cm2
C.36 cm2 D.48 cm2
4.(2024海南中考)如图是跷跷板示意图,支柱OM经过AB的中点O,OM与地面CD垂直于点M,OM=40 cm,当跷跷板的一端A着地时,另一端B离地面的高度为 cm.
5.如图,在△ABC中,AB=4,BC=6,AC=8,D,E,F分别是AB,BC,AC的中点,则△DEF的周长为 .
6.如图,在△ABC中,D,E分别是边AC,AB的中点,连接ED,BD.已知BD平分∠ABC.
求证:BD⊥AC.
7.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3.
(1)求证:BN=DN.
(2)求△ABC的周长.
1.如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是AB,BD,CD,AC的中点,则四边形EFGH的周长为 ( )
A.12 B.14 C.24 D.21
2.(2024宁夏中考)如图,在Rt△ABC中,∠ABC=90°,AB=3 cm,BC=2 cm,点A在直线l1上,点B,C在直线l2上,l1∥l2,动点P从点A出发沿直线l1以1 cm/s的速度向右运动,设运动时间为t s.下列
结论:
①当t=2 s时,四边形ABCP的周长是10 cm;②当t=4 s时,点P到直线l2的距离等于5 cm;③在点P运动过程中,△PBC的面积随着t的增大而增大;④若D,E分别是线段PB,PC的中点,在点P运动过程中,线段DE的长度不变.其中正确的是 ( )
A.①④ B.②③
C.①③ D.②④
3.如图,在 ABCD中,∠C=120°,AB=2,AD=2AB,H,G分别是边DC,BC上的动点,连接AH,HG,E为AH的中点,F为GH的中点,连接EF,则EF的最小值为 ( )
A.2 B.
C.1 D.
4.如图,Rt△ABC中,AB=8,AC=6,∠BAC=90°,D,E分别为AB,AC的中点,P为DE上一点,且满足∠EAP=∠ABP,则PE= ( )
A.1 B.
C. D.2
5.如图,在△ABC中,D,E分别是AC,AB的中点,F是CB延长线上一点,且CF=3BF,连接DB,EF.若∠ACB=90°,AC=12,DE=4.
(1)求证:DE=BF.
(2)求四边形DEFB的周长.
6.(推理能力)如图, 在四边形ABCD中, 对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点 .连接PQ,MN,BD与MN相交于点E,AC与MN相交于点F.
(1) 求证:PQ⊥MN.
(2) 判断△OEF的形状,并说明理由.
【详解答案】
课堂达标
1.C 2.D 3.B 4.80 5.9
6.证明:∵D,E分别是AC,AB的中点,
∴DE是△ABC的中位线,AB=2BE.
∴DE∥BC,BC=2DE.
∴∠CBD=∠EDB.
∵BD平分∠ABC,
∴∠CBD=∠EBD.
∴∠EBD=∠EDB.
∴DE=BE.
∵AB=2BE,∴AB=2DE.
∴AB=BC.
∵D是AC的中点,∴BD⊥AC.
7.(1)证明:∵AN平分∠BAC,
∴∠1=∠2.
∵BN⊥AN,
∴∠ANB=∠AND=90°.
又∵AN=AN,
∴△ABN≌△ADN(ASA).
∴BN=DN.
(2)解:由△ABN≌△ADN,知
AD=AB=10,BN=DN,
∴N为BD的中点.
又∵M是BC的中点,
∴MN为△BCD的中位线.
∴CD=2MN=6.
∴AC=AD+CD=16.
∴△ABC的周长=AB+BC+AC=10+15+16=41.
课后提升
1.A 解析:∵BD⊥CD,BD=4,CD=3,∴BC==5.∵E,F,G,H分别是AB,BD,CD,AC的中点,∴EH=FG=BC,EF=GH=AD.∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC.又∵AD=7,∴四边形EFGH的周长=7+5=12.故选A.
2.A 解析:①当t=2 s时,AP=2 cm,则AP=BC.又因为AP∥BC,所以四边形ABCP是平行四边形.所以PC=AB=
3 cm.所以四边形ABCP的周长为2×(2+3)=10(cm),故①正确.因为平行线间的距离处处相等, AB=3 cm,∠ABC
=90°,所以直线l1与直线l2之间的距离是3 cm.所以当t=4 s时,点P到直线l2的距离仍然是3 cm,故②错误.由上述过程可知,点P到BC的距离为定值3 cm,即△PBC的BC边上的高为3 cm,又因为BC=2 cm,所以△PBC的面积为定值,故③错误.因为D,E分别是线段PB,PC的中点,所以DE是△PBC的中位线,所以DE=BC=1 cm,即线段DE的长度不变,故④正确.故选A.
3.D 解析:如图,连接AG.∵四边形ABCD是平行四边形,∴AB∥CD.∴∠B+∠C=180°.∴∠B=180°-120°=60°.
∵E,F分别是AH,GH的中点,∴EF是△AGH的中位线.∴EF=AG.当AG最小时,EF有最小值,当AG⊥BC时,AG最小,则∠BAG=30°,此时BG=AB=1,AG=BG=.∴EF=AG=,即EF的最小值是.故选D.
4.A 解析:在Rt△ABC中,AB=8,AC=6,由勾股定理,得BC==10.∵D,E分别为AB,AC的中点,∴DE=BC=5.∵∠BAC=90°,∴∠BAP+
∠EAP=90°.∵∠EAP=∠ABP,∴∠BAP+∠ABP=90°.∴∠APB=90°.∵D为AB的中点,∴PD=AB=4.∴PE=DE-DP=1.故选A.
5.(1)证明:∵D,E分别是AC,AB的中点,
∴DE为△ABC的中位线.
∴DE∥BC,DE=BC.
∵CF=3BF,
∴BF=BC.
∴DE=BF.
(2)解:∵D是AC的中点,
AC=12,∴CD=6.
∵DE=4,∴BC=8.
由勾股定理,得
DB==10.
∵DE=BF,DE∥BC,
∴四边形DEFB为平行四边形.
∴四边形DEFB的周长=2×(4+10)=28.
6.(1)证明:如图,连接MP,NP.
∵M,P,N分别是边AB,BC,CD的中点,
∴AM=BM,BP=CP,DN=CN.
∴PM=AC,PN=BD.
又∵AC=BD,∴PM=PN.
∴P在MN的中垂线上.
∵Q是MN的中点,∴PQ⊥MN.
(2)解:△OEF是等腰三角形.
理由如下:∵PM∥AC,
∴∠PMN=∠EFO.
∵PN∥BD,∴∠OEF=∠PNM.
又∵PM=PN,∴∠PMN=∠PNM,
∴∠EFO=∠OEF.
∴△OEF是等腰三角形 .
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
