22.6 正方形 同步练(含答案)2024-2025学年数学冀教版八年级下册
文档属性
| 名称 | 22.6 正方形 同步练(含答案)2024-2025学年数学冀教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 183.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:36:29 | ||
图片预览

文档简介
22.6正方形
正方形的性质
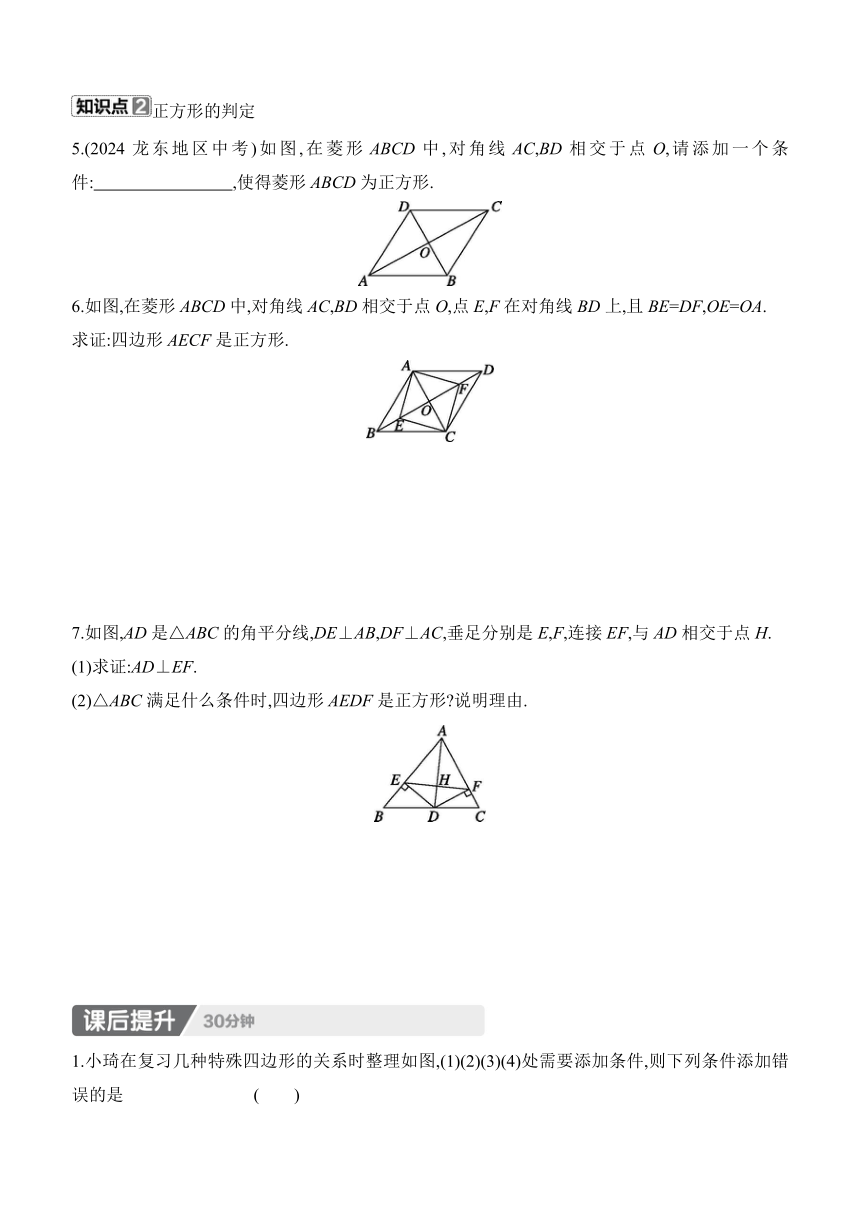
1.如图,在平面直角坐标系中,正方形OABC的顶点O,B的坐标分别是(0,0),(4,0),则顶点C的坐标是 ( )
A.(2,2) B.(2,-2) C.(-2,2) D.(2,-2)
2.如图,正方形ABCD的边长为8,在各边上依次截取AE=BF=CG=DH=6,则四边形EFGH的面积是 ( )
A.34 B.36 C.40 D.100
3.(2024吉林中考)如图,正方形ABCD的对角线AC,BD相交于点O,E是OA的中点,F是OD上一点,连接EF.若∠FEO=45°,则的值为 .
4.(2024徐州中考)如图,四边形ABCD为正方形,点E在BD的延长线上,连接EA,EC.
(1)求证:△EAB≌△ECB.
(2)若∠AEC=45°,求证:DC=DE.
正方形的判定
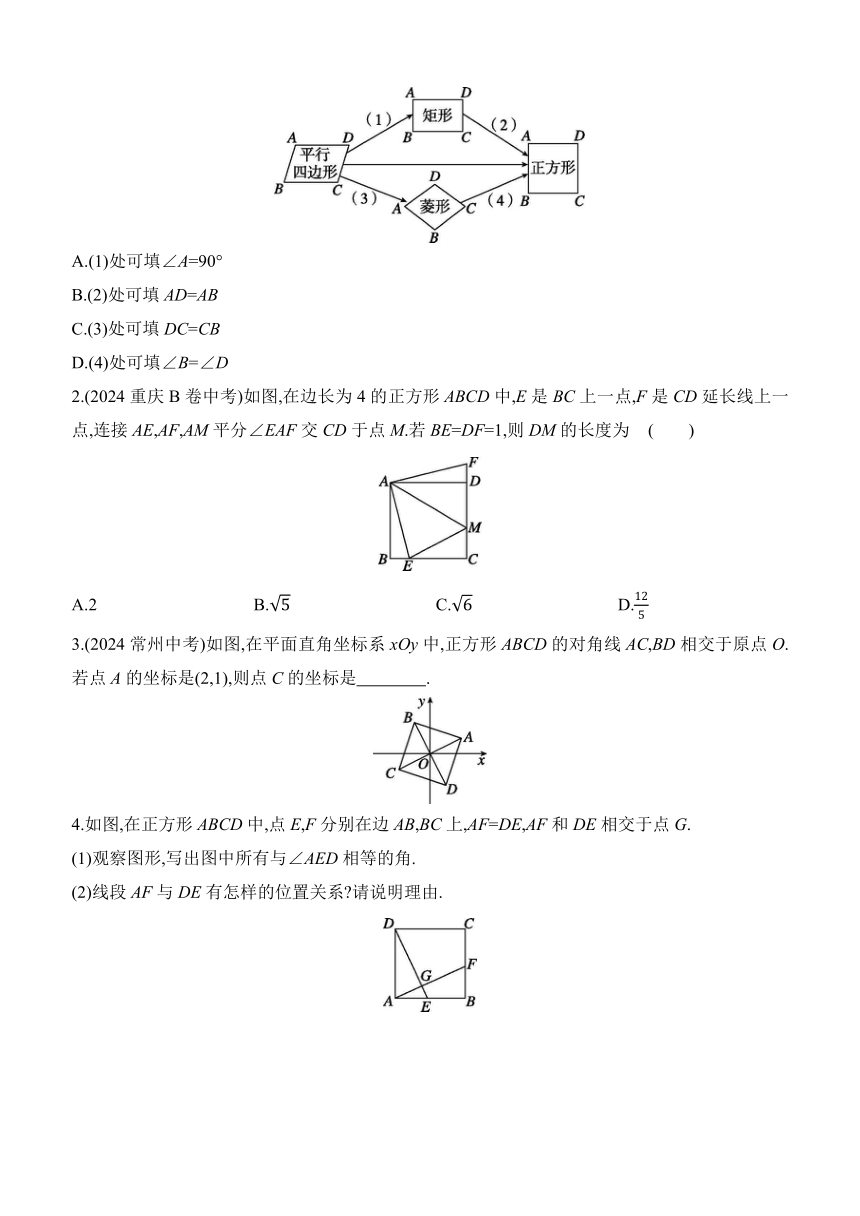
5.(2024龙东地区中考)如图,在菱形ABCD中,对角线AC,BD相交于点O,请添加一个条件: ,使得菱形ABCD为正方形.
6.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA.
求证:四边形AECF是正方形.
7.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF,与AD相交于点H.
(1)求证:AD⊥EF.
(2)△ABC满足什么条件时,四边形AEDF是正方形 说明理由.
1.小琦在复习几种特殊四边形的关系时整理如图,(1)(2)(3)(4)处需要添加条件,则下列条件添加错误的是 ( )
A.(1)处可填∠A=90°
B.(2)处可填AD=AB
C.(3)处可填DC=CB
D.(4)处可填∠B=∠D
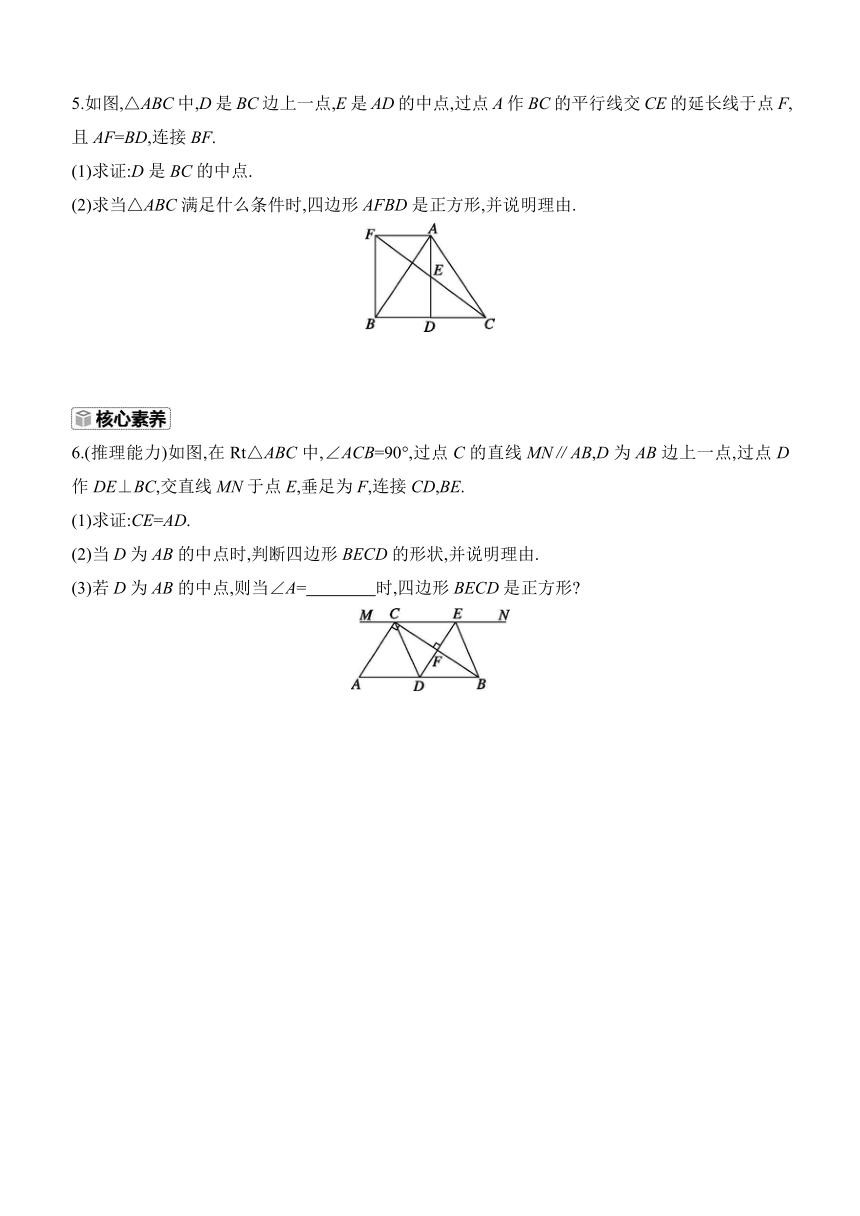
2.(2024重庆B卷中考)如图,在边长为4的正方形ABCD中,E是BC上一点,F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M.若BE=DF=1,则DM的长度为 ( )
A.2 B. C. D.
3.(2024常州中考)如图,在平面直角坐标系xOy中,正方形ABCD的对角线AC,BD相交于原点O.若点A的坐标是(2,1),则点C的坐标是 .
4.如图,在正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G.
(1)观察图形,写出图中所有与∠AED相等的角.
(2)线段AF与DE有怎样的位置关系 请说明理由.
5.如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:D是BC的中点.
(2)求当△ABC满足什么条件时,四边形AFBD是正方形,并说明理由.
6.(推理能力)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)求证:CE=AD.
(2)当D为AB的中点时,判断四边形BECD的形状,并说明理由.
(3)若D为AB的中点,则当∠A= 时,四边形BECD是正方形
【详解答案】
课堂达标
1.B 2.C 3.
4.证明:(1)∵四边形ABCD为正方形,
∴AB=BC,∠ABE=∠CBE=45°.
在△EAB和△ECB中,
∴△EAB≌△ECB(SAS).
(2)∵四边形ABCD为正方形,
∴∠BDC=∠CDA=45°.
∵△EAB≌△ECB,∠AEC=45°,
∴∠CED=∠AED=∠AEC=22.5°.
∵∠BDC=∠CED+∠DCE=45°,
∴∠DCE=45°-22.5°=22.5°.
∴∠CED=∠DCE.∴DC=DE.
5.AC=BD(答案不唯一)
6.证明:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD.
∵BE=DF,∴OE=OF.
∴四边形AECF是菱形.
∵OE=OA,∴OE=OF=OA=OC,∴EF=AC.
∴菱形AECF是正方形.
7.(1)证明:∵AD是△ABC的角平分线,
∴∠EAD=∠FAD.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
在△AED与△AFD中,
∴△AED≌△AFD(AAS).
∴AE=AF.
又∵∠EAD=∠FAD,AH=AH,
∴△AHE≌△AHF(SAS).
∴∠AHE=∠AHF=90°.
∴AD⊥EF.
(2)解:△ABC满足∠BAC=90°时,四边形AEDF是正方形.
理由如下:
∵∠AED=∠AFD=∠BAC=90°,
∴四边形AEDF是矩形.
∵EF⊥AD,
∴矩形AEDF是正方形.
课后提升
1.D 解析:A.有一个角是直角的平行四边形是矩形,∴(1)处可填∠A=90°是正确的,故A不符合题意;B.一组邻边相等的矩形是正方形,∴(2)处可填AD=AB是正确的,故B不符合题意;C.一组邻边相等的平行四边形是菱形,
∴(3)处可填DC=CB是正确的,故C不符合题意;D.有一个角是直角的菱形是正方形,∴∠B=∠D无法判定两角是直角,故D符合题意.故选D.
2.D 解析:∵四边形ABCD是正方形,∴AB=AD,∠ABE=∠ADF=90°.在△ABE和△ADF中,
∴△ABE≌△ADF(SAS).∴AE=AF.∵AM平分∠EAF,∴∠EAM=∠FAM.在△AEM和△AFM中,∴△AEM≌
△AFM(SAS).∴EM=FM.∵四边形ABCD是正方形,∴BC=CD=4,∠BCD=90°.设DM=x,则MC=CD-DM=4-x,CE=BC-BE=4-1=3,EM=FM=FD+DM=1+x,在Rt△MCE中,根据勾股定理,得EM2=MC2+CE2,即(1+x)2=(4-x)2+32,解得x=.故选D.
3.(-2,-1) 解析:如图,过点A,C分别作x轴的垂线AE,CF,∴∠AEO=∠CFO=90°.∵四边形ABCD是正方形,∴OA =OC.∵∠AOE=∠COF,∴△AOE≌△COF(AAS).∴OE=OF,AE=CF.∵点A的坐标是(2,1),∴OE=OF= 2,AE=CF=1.∴点C的坐标为(-2,-1).
4.解:(1)与∠AED相等的角有
∠AFB,∠DAF,∠EDC.
(2)AF⊥DE.理由如下:
在正方形ABCD中,AB=AD,∠DAB=∠B=90°.
在Rt△AED和Rt△BFA中,
∴Rt△AED≌Rt△BFA(HL).
∴∠AED=∠AFB.
∵∠AFB+∠FAB=90°,
∴∠AED+∠FAB=90°.
∴∠AGE=90°,即AF⊥DE.
5.(1)证明:∵AF∥BC,
∴∠AFE=∠DCE.
∵E为AD的中点,∴AE=DE.
在△AEF和△DEC中,
∴△AEF≌△DEC(AAS).
∴AF=CD.
又∵AF=BD,
∴CD=BD.
∴D是BC的中点.
(2)解:△ABC是以AB,AC为腰的等腰直角三角形时,四边形AFBD是正方形.理由如下:
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形.
∵△ABC是等腰直角三角形,D为BC的中点,
∴AD⊥BC,∠ABD=45°.
∴∠ADB=90°.
∴∠BAD=45°=∠ABD,四边形AFBD是矩形.
∴BD=AD.
∴四边形AFBD是正方形.
6.(1)证明:∵DE⊥BC,
∴∠DFB=90°.
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE.
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形.
∴CE=AD.
(2)解:四边形BECD是菱形.
理由:∵D为AB的中点,
∴AD=BD.
∵CE=AD,
∴BD=CE.
∵BD∥CE,
∴四边形BECD是平行四边形.
∵∠ACB=90°,D为AB的中点,
∴CD=BD,
∴四边形BECD是菱形.
(3)45°
正方形的性质
1.如图,在平面直角坐标系中,正方形OABC的顶点O,B的坐标分别是(0,0),(4,0),则顶点C的坐标是 ( )
A.(2,2) B.(2,-2) C.(-2,2) D.(2,-2)
2.如图,正方形ABCD的边长为8,在各边上依次截取AE=BF=CG=DH=6,则四边形EFGH的面积是 ( )
A.34 B.36 C.40 D.100
3.(2024吉林中考)如图,正方形ABCD的对角线AC,BD相交于点O,E是OA的中点,F是OD上一点,连接EF.若∠FEO=45°,则的值为 .
4.(2024徐州中考)如图,四边形ABCD为正方形,点E在BD的延长线上,连接EA,EC.
(1)求证:△EAB≌△ECB.
(2)若∠AEC=45°,求证:DC=DE.
正方形的判定
5.(2024龙东地区中考)如图,在菱形ABCD中,对角线AC,BD相交于点O,请添加一个条件: ,使得菱形ABCD为正方形.
6.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA.
求证:四边形AECF是正方形.
7.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF,与AD相交于点H.
(1)求证:AD⊥EF.
(2)△ABC满足什么条件时,四边形AEDF是正方形 说明理由.
1.小琦在复习几种特殊四边形的关系时整理如图,(1)(2)(3)(4)处需要添加条件,则下列条件添加错误的是 ( )
A.(1)处可填∠A=90°
B.(2)处可填AD=AB
C.(3)处可填DC=CB
D.(4)处可填∠B=∠D
2.(2024重庆B卷中考)如图,在边长为4的正方形ABCD中,E是BC上一点,F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M.若BE=DF=1,则DM的长度为 ( )
A.2 B. C. D.
3.(2024常州中考)如图,在平面直角坐标系xOy中,正方形ABCD的对角线AC,BD相交于原点O.若点A的坐标是(2,1),则点C的坐标是 .
4.如图,在正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G.
(1)观察图形,写出图中所有与∠AED相等的角.
(2)线段AF与DE有怎样的位置关系 请说明理由.
5.如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:D是BC的中点.
(2)求当△ABC满足什么条件时,四边形AFBD是正方形,并说明理由.
6.(推理能力)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)求证:CE=AD.
(2)当D为AB的中点时,判断四边形BECD的形状,并说明理由.
(3)若D为AB的中点,则当∠A= 时,四边形BECD是正方形
【详解答案】
课堂达标
1.B 2.C 3.
4.证明:(1)∵四边形ABCD为正方形,
∴AB=BC,∠ABE=∠CBE=45°.
在△EAB和△ECB中,
∴△EAB≌△ECB(SAS).
(2)∵四边形ABCD为正方形,
∴∠BDC=∠CDA=45°.
∵△EAB≌△ECB,∠AEC=45°,
∴∠CED=∠AED=∠AEC=22.5°.
∵∠BDC=∠CED+∠DCE=45°,
∴∠DCE=45°-22.5°=22.5°.
∴∠CED=∠DCE.∴DC=DE.
5.AC=BD(答案不唯一)
6.证明:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD.
∵BE=DF,∴OE=OF.
∴四边形AECF是菱形.
∵OE=OA,∴OE=OF=OA=OC,∴EF=AC.
∴菱形AECF是正方形.
7.(1)证明:∵AD是△ABC的角平分线,
∴∠EAD=∠FAD.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
在△AED与△AFD中,
∴△AED≌△AFD(AAS).
∴AE=AF.
又∵∠EAD=∠FAD,AH=AH,
∴△AHE≌△AHF(SAS).
∴∠AHE=∠AHF=90°.
∴AD⊥EF.
(2)解:△ABC满足∠BAC=90°时,四边形AEDF是正方形.
理由如下:
∵∠AED=∠AFD=∠BAC=90°,
∴四边形AEDF是矩形.
∵EF⊥AD,
∴矩形AEDF是正方形.
课后提升
1.D 解析:A.有一个角是直角的平行四边形是矩形,∴(1)处可填∠A=90°是正确的,故A不符合题意;B.一组邻边相等的矩形是正方形,∴(2)处可填AD=AB是正确的,故B不符合题意;C.一组邻边相等的平行四边形是菱形,
∴(3)处可填DC=CB是正确的,故C不符合题意;D.有一个角是直角的菱形是正方形,∴∠B=∠D无法判定两角是直角,故D符合题意.故选D.
2.D 解析:∵四边形ABCD是正方形,∴AB=AD,∠ABE=∠ADF=90°.在△ABE和△ADF中,
∴△ABE≌△ADF(SAS).∴AE=AF.∵AM平分∠EAF,∴∠EAM=∠FAM.在△AEM和△AFM中,∴△AEM≌
△AFM(SAS).∴EM=FM.∵四边形ABCD是正方形,∴BC=CD=4,∠BCD=90°.设DM=x,则MC=CD-DM=4-x,CE=BC-BE=4-1=3,EM=FM=FD+DM=1+x,在Rt△MCE中,根据勾股定理,得EM2=MC2+CE2,即(1+x)2=(4-x)2+32,解得x=.故选D.
3.(-2,-1) 解析:如图,过点A,C分别作x轴的垂线AE,CF,∴∠AEO=∠CFO=90°.∵四边形ABCD是正方形,∴OA =OC.∵∠AOE=∠COF,∴△AOE≌△COF(AAS).∴OE=OF,AE=CF.∵点A的坐标是(2,1),∴OE=OF= 2,AE=CF=1.∴点C的坐标为(-2,-1).
4.解:(1)与∠AED相等的角有
∠AFB,∠DAF,∠EDC.
(2)AF⊥DE.理由如下:
在正方形ABCD中,AB=AD,∠DAB=∠B=90°.
在Rt△AED和Rt△BFA中,
∴Rt△AED≌Rt△BFA(HL).
∴∠AED=∠AFB.
∵∠AFB+∠FAB=90°,
∴∠AED+∠FAB=90°.
∴∠AGE=90°,即AF⊥DE.
5.(1)证明:∵AF∥BC,
∴∠AFE=∠DCE.
∵E为AD的中点,∴AE=DE.
在△AEF和△DEC中,
∴△AEF≌△DEC(AAS).
∴AF=CD.
又∵AF=BD,
∴CD=BD.
∴D是BC的中点.
(2)解:△ABC是以AB,AC为腰的等腰直角三角形时,四边形AFBD是正方形.理由如下:
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形.
∵△ABC是等腰直角三角形,D为BC的中点,
∴AD⊥BC,∠ABD=45°.
∴∠ADB=90°.
∴∠BAD=45°=∠ABD,四边形AFBD是矩形.
∴BD=AD.
∴四边形AFBD是正方形.
6.(1)证明:∵DE⊥BC,
∴∠DFB=90°.
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE.
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形.
∴CE=AD.
(2)解:四边形BECD是菱形.
理由:∵D为AB的中点,
∴AD=BD.
∵CE=AD,
∴BD=CE.
∵BD∥CE,
∴四边形BECD是平行四边形.
∵∠ACB=90°,D为AB的中点,
∴CD=BD,
∴四边形BECD是菱形.
(3)45°
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
