22.7 多边形的内角和与外角和 同步练(含答案)2024-2025学年数学冀教版八年级下册
文档属性
| 名称 | 22.7 多边形的内角和与外角和 同步练(含答案)2024-2025学年数学冀教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 212.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:36:51 | ||
图片预览

文档简介
22.7多边形的内角和与外角和
多边形的对角线
1.若从一多边形的一个顶点出发,最多可引10条对角线,则它是 ( )
A.十三边形 B.十二边形
C.十一边形 D.十边形
2.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形的边数是 ( )
A.8 B.7 C.6 D.5
多边形的内角和
3.一个七边形的内角和等于 ( )
A.540° B.900°
C.980° D.1 080°
4.如果一个多边形的内角和等于一个三角形的外角和的两倍,那么这个多边形是 ( )
A.三角形 B.四边形
C.五边形 D.六边形
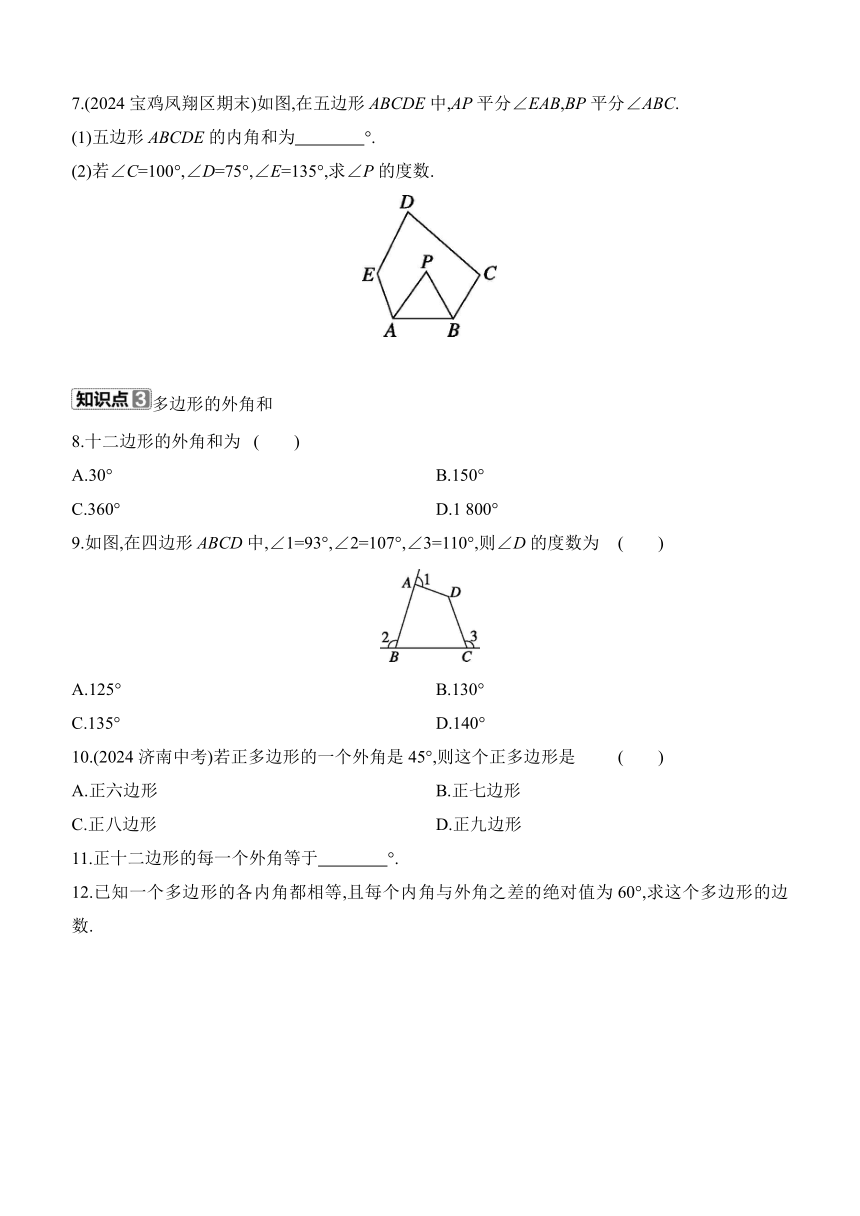
5.如图,∠F=90°,则∠A+∠B+∠C+∠D+∠E的度数为 ( )
A.90° B.180° C.270° D.360°
6.如图,∠1+∠2+∠3+∠4+∠5+∠6= ( )
A.180° B.270° C.360° D.540°
7.(2024宝鸡凤翔区期末)如图,在五边形ABCDE中,AP平分∠EAB,BP平分∠ABC.
(1)五边形ABCDE的内角和为 °.
(2)若∠C=100°,∠D=75°,∠E=135°,求∠P的度数.
多边形的外角和
8.十二边形的外角和为 ( )
A.30° B.150°
C.360° D.1 800°
9.如图,在四边形ABCD中,∠1=93°,∠2=107°,∠3=110°,则∠D的度数为 ( )
A.125° B.130°
C.135° D.140°
10.(2024济南中考)若正多边形的一个外角是45°,则这个正多边形是 ( )
A.正六边形 B.正七边形
C.正八边形 D.正九边形
11.正十二边形的每一个外角等于 °.
12.已知一个多边形的各内角都相等,且每个内角与外角之差的绝对值为60°,求这个多边形的边数.
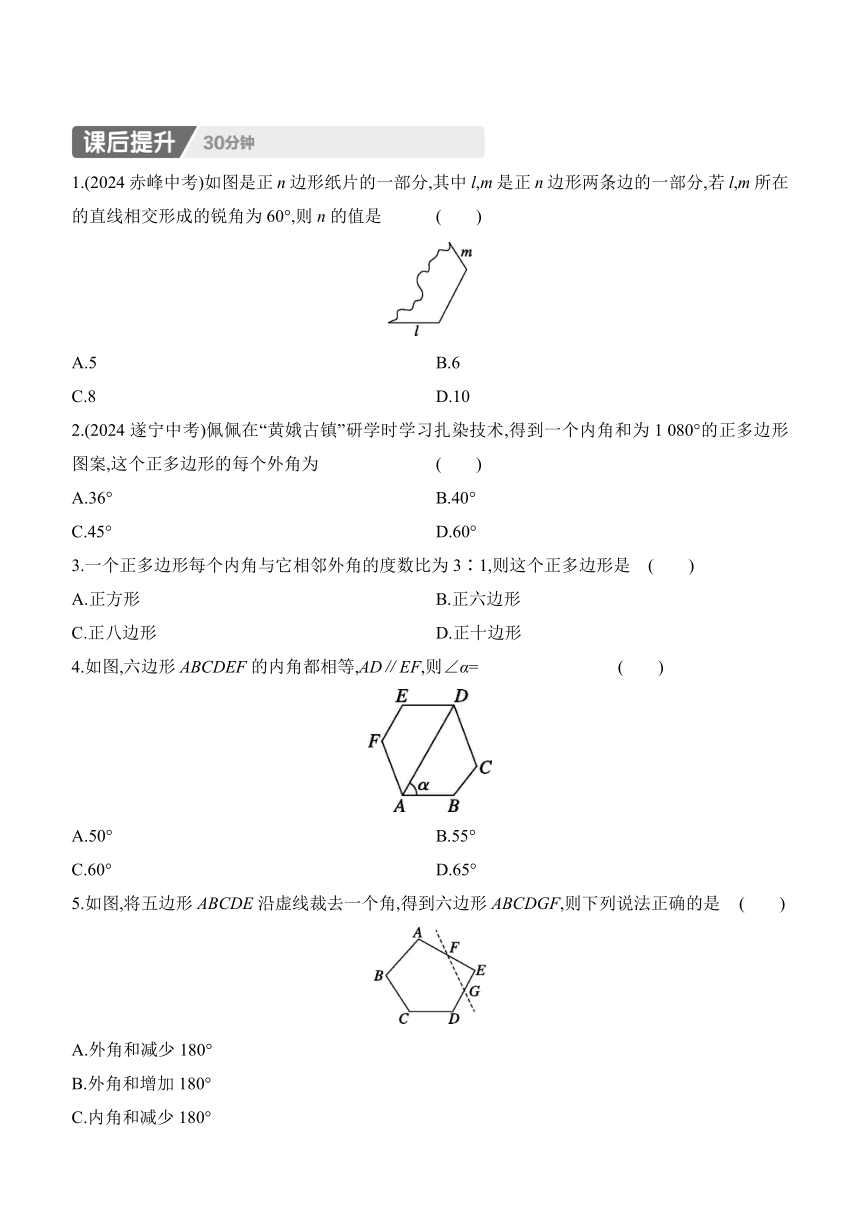
1.(2024赤峰中考)如图是正n边形纸片的一部分,其中l,m是正n边形两条边的一部分,若l,m所在的直线相交形成的锐角为60°,则n的值是 ( )
A.5 B.6
C.8 D.10
2.(2024遂宁中考)佩佩在“黄娥古镇”研学时学习扎染技术,得到一个内角和为1 080°的正多边形图案,这个正多边形的每个外角为 ( )
A.36° B.40°
C.45° D.60°
3.一个正多边形每个内角与它相邻外角的度数比为3∶1,则这个正多边形是 ( )
A.正方形 B.正六边形
C.正八边形 D.正十边形
4.如图,六边形ABCDEF的内角都相等,AD∥EF,则∠α= ( )
A.50° B.55°
C.60° D.65°
5.如图,将五边形ABCDE沿虚线裁去一个角,得到六边形ABCDGF,则下列说法正确的是 ( )
A.外角和减少180°
B.外角和增加180°
C.内角和减少180°
D.内角和增加180°
6.(2024宁夏中考)如图,在正五边形ABCDE的内部,以CD为边作正方形CDFH,连接BH,则∠BHC= °.
7.已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗 若对,求出边数n;若不对,说明理由.
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x.
8.(推理能力)如图1,直线l与△ABC的边AC,AB分别相交于点D,E(都不与点A重合).
(1)若∠A=64°,
①求∠1+∠2的度数;
②如图2,直线m与边AB,AC相交得到∠3和∠4,直接写出∠3+∠4的度数.
(2)如图3,EO,DO分别平分∠BED和∠CDE,写出∠EOD和∠A的数量关系,并说明理由.
(3)如图4,在四边形BCDE中,M,N分别是线段DC、线段BE上的点,NG,MG分别平分∠BNM和∠CMN,直接写出∠NGM与∠E,∠D的关系.
【详解答案】
课堂达标
1.A 2.B 3.B 4.D 5.C 6.C
7.解:(1)540
(2)∵在五边形ABCDE中,∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,∴∠EAB+∠ABC =230°.
∵AP平分∠EAB,BP平分∠ABC,
∴∠PAB=∠EAB,∠PBA=∠ABC.
∴∠PAB+∠PBA=115°.
∴∠P=180°-(∠PAB+∠PBA)=65°.
8.C 9.B 10.C 11.30
12.解:设每个内角为x°,则每个外角为180°-x°.
由|x-(180-x)|=60,
得x=120或60.
当x=120时,每个外角为60°,边数为6;
当x=60时,每个外角为120°,边数为3.
所以这个多边形的边数为3或6.
课后提升
1.B 解析:如图,直线l,m相交于点A,则∠A=60°.∵正多边形的每个内角相等,∴正多边形的每个外角也相等,
∠1=∠2==60°.∴n==6.故选B.
2.C 解析:设这个正多边形的边数为n.由题意,得(n-2)·180°=1 080°,解得n=8,则360°÷8=45°,即这个正多边形的每个外角为45°.故选C.
3.C 解析:∵一个正多边形每个内角与它相邻外角的度数比为3∶1,∴设每个外角是x°,则每个内角是3x°.根据题意,得x+3x=180,解得x=45,外角个数为360°÷45°=8,∴该正多边形为正八边形.故选C.
4.C 解析:∵六边形ABCDEF的内角都相等,∴∠F=∠FAB==120°.∵AD∥EF,∴∠F+∠FAD=180°.
∴∠FAD=180°-∠F=60°.∴∠α=∠FAB-∠FAD=60°.故选C.
5.D 解析:将五边形ABCDE沿虚线裁去一个角,得到六边形ABCDGF,则五边形ABCDE的内角和为(5-2)×180°=540°,六边形ABCDGF的内角和为(6-2)×180°=720°,∴720°-540°=180°.∵五边形ABCDE、六边形ABCDGF的外角和都是360°,∴将五边形ABCDE沿虚线裁去一个角,得到六边形ABCDGF,内角和增加180°,外角和不变.故选D.
6.81 解析:在正五边形ABCDE中,∠BCD=180°-(360°÷5)=108°.∵∠HCD=90°,∴∠BCH=∠BCD-∠HCD=18°.∵BC=HC,∴∠BHC=∠CBH=(180°-∠BCH)=81°.
7.解:(1)∵360°÷180°=2,
630°÷180°=3……90°,
∴甲的说法对,乙的说法不对.
360°÷180°+2
=2+2
=4.
故甲同学说的边数n是4.
(2)依题意有(n+x-2)×180°-(n-2)×180°=540°,
解得x=3.
故x的值是3.
8.解:(1)①∵∠1=∠A+∠ADE,∠2=∠A+∠AED,
∴∠1+∠2=∠A+∠ADE+∠AED+∠A.
∵∠A+∠ADE+∠AED=180°,∠A=64°,
∴∠1+∠2
=∠A+180°
=64°+180°
=244°.
②∠3+∠4=244°.
(2)∠EOD=90°-∠A.理由:
由(1)可得∠BED+∠CDE=180°+∠A.
∵EO,DO分别平分∠BED和∠CDE,
∴∠OED=∠BED,∠EDO=∠CDE.
∴∠OED+∠EDO
=(∠BED+∠CDE)
=×(180°+∠A)
=90°+∠A,
∴∠EOD=180°-(∠OED+∠EDO)=
180°-=90°-∠A.
(3)∠E+∠D+2∠NGM=360°.
解法提示:由(1)知∠BNM+
∠CMN=∠D+∠E.
∵NG,MG分别是∠BNM,∠CMN的平分线,
∴∠BNG=∠MNG=∠BNM,
∠CMG=∠NMG=∠CMN.
∴∠NGM=180°-(∠MNG+∠NMG)
=180°-(∠BNM+∠CMN)
=180°-(∠D+∠E).
∴2∠NGM+∠D+∠E=360°.
多边形的对角线
1.若从一多边形的一个顶点出发,最多可引10条对角线,则它是 ( )
A.十三边形 B.十二边形
C.十一边形 D.十边形
2.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形的边数是 ( )
A.8 B.7 C.6 D.5
多边形的内角和
3.一个七边形的内角和等于 ( )
A.540° B.900°
C.980° D.1 080°
4.如果一个多边形的内角和等于一个三角形的外角和的两倍,那么这个多边形是 ( )
A.三角形 B.四边形
C.五边形 D.六边形
5.如图,∠F=90°,则∠A+∠B+∠C+∠D+∠E的度数为 ( )
A.90° B.180° C.270° D.360°
6.如图,∠1+∠2+∠3+∠4+∠5+∠6= ( )
A.180° B.270° C.360° D.540°
7.(2024宝鸡凤翔区期末)如图,在五边形ABCDE中,AP平分∠EAB,BP平分∠ABC.
(1)五边形ABCDE的内角和为 °.
(2)若∠C=100°,∠D=75°,∠E=135°,求∠P的度数.
多边形的外角和
8.十二边形的外角和为 ( )
A.30° B.150°
C.360° D.1 800°
9.如图,在四边形ABCD中,∠1=93°,∠2=107°,∠3=110°,则∠D的度数为 ( )
A.125° B.130°
C.135° D.140°
10.(2024济南中考)若正多边形的一个外角是45°,则这个正多边形是 ( )
A.正六边形 B.正七边形
C.正八边形 D.正九边形
11.正十二边形的每一个外角等于 °.
12.已知一个多边形的各内角都相等,且每个内角与外角之差的绝对值为60°,求这个多边形的边数.
1.(2024赤峰中考)如图是正n边形纸片的一部分,其中l,m是正n边形两条边的一部分,若l,m所在的直线相交形成的锐角为60°,则n的值是 ( )
A.5 B.6
C.8 D.10
2.(2024遂宁中考)佩佩在“黄娥古镇”研学时学习扎染技术,得到一个内角和为1 080°的正多边形图案,这个正多边形的每个外角为 ( )
A.36° B.40°
C.45° D.60°
3.一个正多边形每个内角与它相邻外角的度数比为3∶1,则这个正多边形是 ( )
A.正方形 B.正六边形
C.正八边形 D.正十边形
4.如图,六边形ABCDEF的内角都相等,AD∥EF,则∠α= ( )
A.50° B.55°
C.60° D.65°
5.如图,将五边形ABCDE沿虚线裁去一个角,得到六边形ABCDGF,则下列说法正确的是 ( )
A.外角和减少180°
B.外角和增加180°
C.内角和减少180°
D.内角和增加180°
6.(2024宁夏中考)如图,在正五边形ABCDE的内部,以CD为边作正方形CDFH,连接BH,则∠BHC= °.
7.已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗 若对,求出边数n;若不对,说明理由.
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x.
8.(推理能力)如图1,直线l与△ABC的边AC,AB分别相交于点D,E(都不与点A重合).
(1)若∠A=64°,
①求∠1+∠2的度数;
②如图2,直线m与边AB,AC相交得到∠3和∠4,直接写出∠3+∠4的度数.
(2)如图3,EO,DO分别平分∠BED和∠CDE,写出∠EOD和∠A的数量关系,并说明理由.
(3)如图4,在四边形BCDE中,M,N分别是线段DC、线段BE上的点,NG,MG分别平分∠BNM和∠CMN,直接写出∠NGM与∠E,∠D的关系.
【详解答案】
课堂达标
1.A 2.B 3.B 4.D 5.C 6.C
7.解:(1)540
(2)∵在五边形ABCDE中,∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,∴∠EAB+∠ABC =230°.
∵AP平分∠EAB,BP平分∠ABC,
∴∠PAB=∠EAB,∠PBA=∠ABC.
∴∠PAB+∠PBA=115°.
∴∠P=180°-(∠PAB+∠PBA)=65°.
8.C 9.B 10.C 11.30
12.解:设每个内角为x°,则每个外角为180°-x°.
由|x-(180-x)|=60,
得x=120或60.
当x=120时,每个外角为60°,边数为6;
当x=60时,每个外角为120°,边数为3.
所以这个多边形的边数为3或6.
课后提升
1.B 解析:如图,直线l,m相交于点A,则∠A=60°.∵正多边形的每个内角相等,∴正多边形的每个外角也相等,
∠1=∠2==60°.∴n==6.故选B.
2.C 解析:设这个正多边形的边数为n.由题意,得(n-2)·180°=1 080°,解得n=8,则360°÷8=45°,即这个正多边形的每个外角为45°.故选C.
3.C 解析:∵一个正多边形每个内角与它相邻外角的度数比为3∶1,∴设每个外角是x°,则每个内角是3x°.根据题意,得x+3x=180,解得x=45,外角个数为360°÷45°=8,∴该正多边形为正八边形.故选C.
4.C 解析:∵六边形ABCDEF的内角都相等,∴∠F=∠FAB==120°.∵AD∥EF,∴∠F+∠FAD=180°.
∴∠FAD=180°-∠F=60°.∴∠α=∠FAB-∠FAD=60°.故选C.
5.D 解析:将五边形ABCDE沿虚线裁去一个角,得到六边形ABCDGF,则五边形ABCDE的内角和为(5-2)×180°=540°,六边形ABCDGF的内角和为(6-2)×180°=720°,∴720°-540°=180°.∵五边形ABCDE、六边形ABCDGF的外角和都是360°,∴将五边形ABCDE沿虚线裁去一个角,得到六边形ABCDGF,内角和增加180°,外角和不变.故选D.
6.81 解析:在正五边形ABCDE中,∠BCD=180°-(360°÷5)=108°.∵∠HCD=90°,∴∠BCH=∠BCD-∠HCD=18°.∵BC=HC,∴∠BHC=∠CBH=(180°-∠BCH)=81°.
7.解:(1)∵360°÷180°=2,
630°÷180°=3……90°,
∴甲的说法对,乙的说法不对.
360°÷180°+2
=2+2
=4.
故甲同学说的边数n是4.
(2)依题意有(n+x-2)×180°-(n-2)×180°=540°,
解得x=3.
故x的值是3.
8.解:(1)①∵∠1=∠A+∠ADE,∠2=∠A+∠AED,
∴∠1+∠2=∠A+∠ADE+∠AED+∠A.
∵∠A+∠ADE+∠AED=180°,∠A=64°,
∴∠1+∠2
=∠A+180°
=64°+180°
=244°.
②∠3+∠4=244°.
(2)∠EOD=90°-∠A.理由:
由(1)可得∠BED+∠CDE=180°+∠A.
∵EO,DO分别平分∠BED和∠CDE,
∴∠OED=∠BED,∠EDO=∠CDE.
∴∠OED+∠EDO
=(∠BED+∠CDE)
=×(180°+∠A)
=90°+∠A,
∴∠EOD=180°-(∠OED+∠EDO)=
180°-=90°-∠A.
(3)∠E+∠D+2∠NGM=360°.
解法提示:由(1)知∠BNM+
∠CMN=∠D+∠E.
∵NG,MG分别是∠BNM,∠CMN的平分线,
∴∠BNG=∠MNG=∠BNM,
∠CMG=∠NMG=∠CMN.
∴∠NGM=180°-(∠MNG+∠NMG)
=180°-(∠BNM+∠CMN)
=180°-(∠D+∠E).
∴2∠NGM+∠D+∠E=360°.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
