第十九章 平面直角坐标系 评估测试卷 (含答案)冀教版数学八年级下册
文档属性
| 名称 | 第十九章 平面直角坐标系 评估测试卷 (含答案)冀教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 911.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 00:00:00 | ||
图片预览




文档简介
第十九章 平面直角坐标系 评估测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
1.根据下列表述,能确定位置的是 ( )
A.兴庆路
B.负二层停车场
C.太平洋影城3号厅2排
D.东经106°,北纬32°
2.(2024邯郸广平县月考)在平面直角坐标系中,点P(x,y)在第二象限,且点P到x轴和y轴的距离分别是3和4,则点P的坐标为( )
A.(4,-3) B.(-3,4)
C.(3,-4) D.(-4,3)
3.某小区的圆形花园中间有两条互相垂直的小路,园丁在花园中栽种了8棵桂花,如图所示.若A,B两处桂花的位置关于小路对称,在分别以两条小路为x,y轴的平面直角坐标系内,若点A的坐标为(-6,2),则点B的坐标为 ( )
A.(6,2) B.(-6,-2)
C.(2,6) D.(2,-6)
4.如图,在长方形ABCD中,A(-3,2),B(3,2),C(3,-1),则点D的坐标为 ( )
A.(-2,-1) B.(4,-1)
C.(-3,-2) D.(-3,-1)
5.(2024甘肃中考)敦煌文书是华夏民族引以为傲的艺术瑰宝,其中敦煌《算经》中出现的《田积表》部分如图1所示,它以表格形式将长方形土地的面积直观展示,可迅速准确地查出边长10步到60步的长方形田地面积,极大地提高了农田面积的测量效率.如图2是复原的部分《田积表》,表中对田地的长和宽都用步来表示,A区域表示的是长15步、宽16步的田地面积为一亩,用有序数对记为(15,16),那么有序数对记为(12,17)对应的田地面积为 ( )
A.一亩八十步 B.一亩二十步
C.半亩七十八步 D.半亩八十四步
6.已知点A(a-2,a+1),点B(2,3),直线AB∥x轴,则a的值是 ( )
A.1 B.2 C.3 D.4
7.已知A(a,-2)和B(4,b)关于原点对称,则a-b的值为 ( )
A.6 B.-6 C.2 D.-4
8.将线段AB在平面直角坐标系中平移,已知点A(-2,2),B(0,0),将线段平移后,其两个端点的对应点分别为A'(-1,4),B'(1,2),则它的平移情况是 ( )
A.向左平移了1个单位长度,向上平移了2个单位长度
B.向右平移了1个单位长度,向下平移了2个单位长度
C.向右平移了1个单位长度,向上平移了2个单位长度
D.向左平移了1个单位长度,向下平移了2个单位长度
9.已知点P(2-a,3a+6)到两坐标轴的距离相等,则点P的坐标是 ( )
A.(3,3) B.(3,-3)
C.(6,-6) D.(3,3)或(6,-6)
10.如果一个图形上各点的横坐标保持不变,而纵坐标分别都变为原来的,那么所得的图形与原图形相比 ( )
A.形状不变,图形缩小为原来的一半
B.形状不变,图形放大为原来的2倍
C.整个图形被横向压缩为原来的一半
D.整个图形被纵向压缩为原来的一半
11.如图,已知点A(-1,0),B(0,2),A与A'关于y轴对称,连接A'B,现将线段A'B以点A'为中心顺时针旋转90°得到A'B',则点B的对应点B'的坐标为 ( )
A.(3,1) B.(2,1)
C.(4,1) D.(3,2)
12.我们规定:在平面直角坐标系中,任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1-x2|+|y1-y2|.例如右图中,点M(-2,3)与点N(1,-1)之间的折线距离d(M,N)=|-2-1|+|3-(-1)|
=3+4=7.已知点P(-3,4),若点Q的坐标为(1,t),且d(P,Q)=8,则t的值为 ( )
A.0 B.-1
C.-1或7 D.0或8
二、填空题(本大题共4个小题,每小题3分,共12分)
13.已知点P在x轴上,且点P到y轴的距离等于6,则点P的坐标是 .
14.(2024邯郸永年区期末)“在生活的舞台上,我们都是不屈不挠的拳击手,面对无尽的挑战,挥洒汗水,拼搏向前!”2024年的春节档《热辣滚烫》展现了角色坚韧不拔的精神面貌.小明、小华、小亮三人也观看了此电影,如图是利用平面直角坐标系画出的影院内分布图,若分别以正东、正北方向为x轴、y轴的正方向,建立平面直角坐标系xOy,他们是这样描述自己的座位:
①小明:表示我座位的坐标为(-2,3);
②小华:在小明的座位向右走4个座位,再向上走2个座位,就可以找到我了;
③小亮:小旗帜所在的位置就是我的座位了.
则小亮座位的坐标为 .
15.如图,在平面直角坐标系中,将三角形ABC平移至三角形A1B1C1,P(a,b)是三角形ABC内一点,经平移后得到三角形A1B1C1内的对应点P1(a+8,b-5).若点A1的坐标为(5,-1),则点A的坐标为 .
16.如图,在平面直角坐标系中,A(6,0),B(0,y),连接AB,过点A作AC⊥AB.若AC=AB,x轴上的一点M(-1,0),连接CM,当点B在y轴上移动时,CM的最小值为 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)已知平面直角坐标系中有一点A(m-1,2m+3).
(1)点A在x轴上时,求点A的坐标.
(2)点A在第二、四象限的角平分线上时,求点A的坐标.
(3)点A到y轴的距离为2时,求点A的坐标.
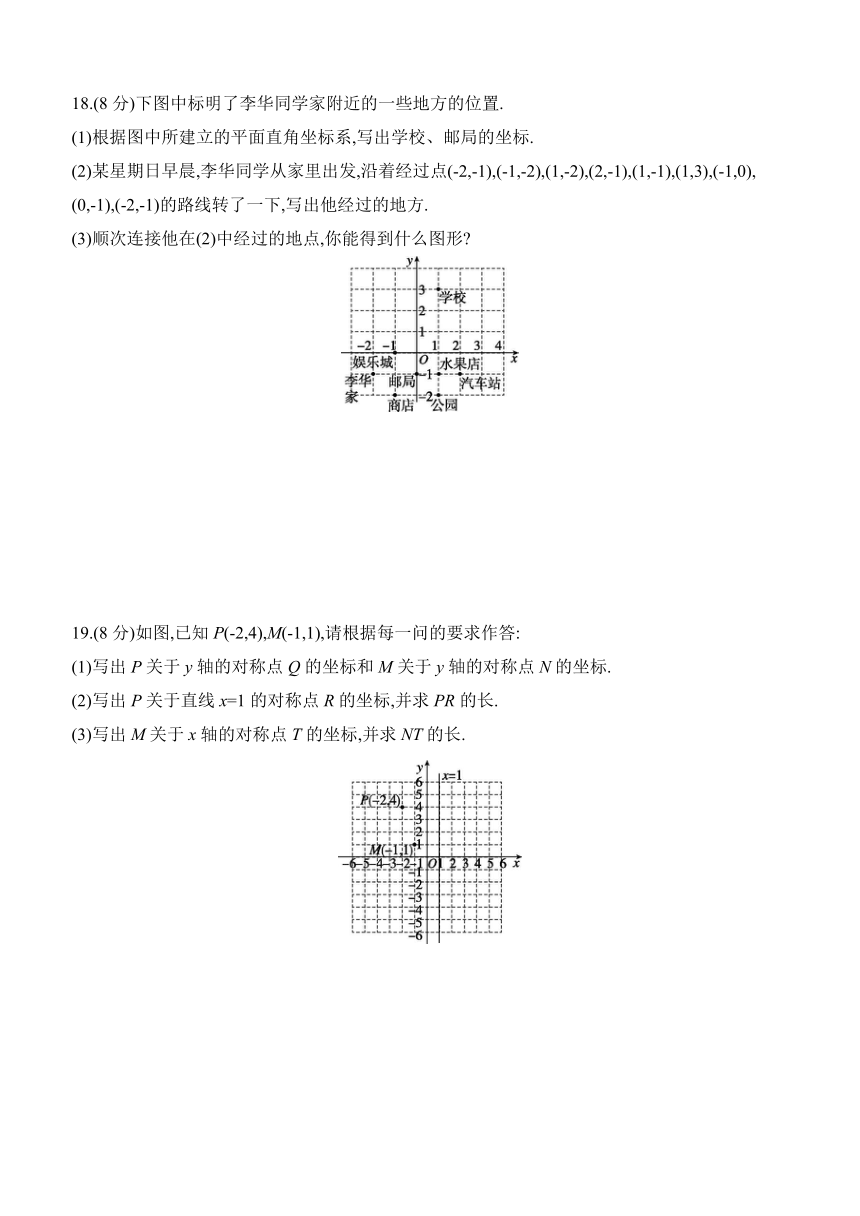
18.(8分)下图中标明了李华同学家附近的一些地方的位置.
(1)根据图中所建立的平面直角坐标系,写出学校、邮局的坐标.
(2)某星期日早晨,李华同学从家里出发,沿着经过点(-2,-1),(-1,-2),(1,-2),(2,-1),(1,-1),(1,3),(-1,0),
(0,-1),(-2,-1)的路线转了一下,写出他经过的地方.
(3)顺次连接他在(2)中经过的地点,你能得到什么图形
19.(8分)如图,已知P(-2,4),M(-1,1),请根据每一问的要求作答:
(1)写出P关于y轴的对称点Q的坐标和M关于y轴的对称点N的坐标.
(2)写出P关于直线x=1的对称点R的坐标,并求PR的长.
(3)写出M关于x轴的对称点T的坐标,并求NT的长.
20.(8分)如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标.
(2)如果点P的坐标是(-a,0),其中021.(8分)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(1,2),B(3,1)(每个方格的边长均为1个单位长度).
(1)将△OAB向右平移1个单位长度后得到△O1A1B1,请画出△O1A1B1.
(2)将△O1A1B1各顶点的横、纵坐标都乘2,各对应顶点的坐标为O2 ,A2 ,B2 ;在直角坐标系中画出△O2A2B2.
(3)P(a,b)为△OAB内一点,则按题(1)(2)变换后点P在△O2A2B2中的对应点P'的坐标为 .
22.(10分)【观察·发现】如图,观察下列各点的排列规律:
A(0,1),A1(2,0),A2(3,2),A3(5,1),A4(6,3),….
【归纳·应用】
(1)点A6的坐标为 ;点A12的坐标为 .
(2)若点A2n的坐标为(3 036,1 013),求n的值.
23.(10分)在平面直角坐标系中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”,例如,点P(1,4)的“3级关联点”为Q(3×1+4,1+3×4),即Q(7,13).
(1)若点B的“2级关联点”是B'(3,3),求点B的坐标.
(2)已知点M(m-1,2m)的“-3级关联点”N位于y轴上,求点N的坐标.
24.(12分)在平面直角坐标系中,点A(x,y),点A'(x',y'),若x'=x+m,y'=y+n,即点A'(x+m,y+n),则表示A到点A'的一个平移.例如:点A(x,y),点A'(x',y'),若x'=x+1,y'=y-2,则表示点A向右平移1个单位长度,再向下平移2个单位长度得到点A'.
根据上述定义,探究下列问题:
(1)已知点A(x,y),A'(x-3,y),则线段AA'的长度是 .
(2)已知点A(x,y),A'(x+2,y-1),则线段AA'的长度是 .
(3)长方形AOCB在平面直角坐标系中的位置如图所示,A(0,2),C(4,0),点A'(x',y'),若x'=x+m,y'=
y-2m(m均为正数),点A'(x',y')能否在△OCB的直角边上 若能,求m的值,若不能,请说明理由.
【详解答案】
1.D
2.D 解析:∵点P(x,y)在第二象限,点P到x轴和y轴的距离分别是3和4,∴点P的横坐标是-4,纵坐标是3,即点P的坐标为(-4,3).故选D.
3.A 解析:由题意,得点B的坐标为(6,2).故选A.
4.D 解析:∵A(-3,2),B(3,2),∴AB=6,AB∥x轴.∵四边形ABCD是长方形,∴CD=AB=6,AB∥CD∥x轴.同理,AD∥BC∥y轴.∵C(3,-1),∴点D的坐标为(-3,-1).故选D.
5.D 解析:根据(15,16)对应的田地面积为一亩,可得(12,17)对应的田地面积是半亩八十四步.故选D.
6.B 解析:∵点A(a-2,a+1),点B(2,3),直线AB∥x轴,∴a+1=3.∴a=2.故选B.
7.B 解析:∵A(a,-2)和B(4,b)关于原点对称,∴a=-4,b=-(-2)=2.∴a-b=-4-2=-6.故选B.
8.C
9.D 解析:由题意,得|2-a|=|3a+6|,则2-a=3a+6或2-a=-3a-6,所以a=-1或a=-4.所以点P的坐标是(3,3)或(6,-6).故选D.
10.D 解析:∵横坐标不变,∴图形横向不变.∵纵坐标变为原来的,∴图形被纵向压缩为原来的一半.故选D.
11.A 解析:∵点A的坐标为(-1,0),点A'和点A关于y轴对称,∴点A'的坐标为(1,0).∴OA'=1.∵点B的坐标为(0,2),∴OB=2.如图,过点B'作x轴的垂线,垂足为M.由旋转可知,A'B=A'B',∠BA'B'=90°,∴∠BA'O+∠B'A'M=
∠BA'O+∠A'BO=90°,∴∠B'A'M=∠A'BO.在△A'BO和△B'A'M中,∴△A'BO≌△B'A'M(AAS).∴B'M=A'O=1,A'M=BO=2.∴OM=1+2=3.∴点B'的坐标为(3,1).故选A.
12.D 解析:∵P(-3,4),Q(1,t),d(P,Q)=8,∴|-3-1|+|4-t|=8,解得t=0或t=8.故选D.
13.(6,0)或(-6,0) 解析:∵点P在x轴上,且点P到y轴的距离等于6,∴xP=±6,yP=0.∴点P的坐标是(6,0)或(-6,0).
14.(2,0) 解析:∵小明座位的坐标为(-2,3),如图,建立平面直角坐标系.∴小华座位的坐标为(2,5).∵小旗帜位置的坐标为(2,0),即小亮座位的坐标为(2,0).
15.(-3,4)
16.6 解析:如图,过点C作CD⊥x轴于点D.∵∠ACD+∠CAD=∠CAD+∠BAO=90°,∴∠ACD=∠BAO.
∵∠ADC=∠BOA=90°,AC=BA,∴△ACD≌△BAO(AAS).∴CD=AO.∵A(6,0),∴CD=AO=6.∴点C在平行于x轴且与x轴距离为6的直线上运动,当MC垂直于这条直线时,CM最短,此时CM=CD=6.
17.解:(1)由题意,得2m+3=0,
解得m=-,故m-1=-,
所以点A的坐标为.
(2)由题意,得(m-1)+(2m+3)=0,
解得m=-,
故m-1=-,2m+3=,
所以点A的坐标为.
(3)由题意,得|m-1|=2,
解得m=3或m=-1,
故m-1=2,2m+3=9或m-1=-2,2m+3=1,
所以点A的坐标为(2,9)或(-2,1).
18.解:(1)学校(1,3),邮局(0,-1).
(2)李华家、商店、公园、汽车站、水果店、学校、娱乐城、邮局、李华家.
(3)得到的图形如图所示,像一只帆船.
19.解:(1)如图,点Q、点N即为所求,Q(2,4),N(1,1).
(2)如图,点R即为所求,R(4,4),PR=6.
(3)如图,点T即为所求.T(-1,-1),NT==2.
20.解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2).
(2)如图,当0∴P1(a,0).
又∵P1与P2关于l:直线x=3对称,
设P2(x,0),可得=3,即x=6-a,∴P2(6-a,0).
∴PP2=6-a-(-a)=6-a+a=6.
21.解:(1)如图,△O1A1B1即为所求作三角形.
(2)(2,0) (4,4) (8,2)
如图,△O2A2B2即为所求作三角形.
(3)(2a+2,2b)
22.解:(1)(9,4) (18,7)
(2)A(0,1),A1(2,0),A2(3,2),A3(5,1),A4(6,3),…,
且A(0,1),A2(1×3,1+1),A4(2×3,1+2),A6(3×3,1+3),…,以此类推,
A2n,即A2n(3n,n+1),
∵点A2n的坐标为(3 036,1 013),
∴3n=3 036,解得n=1 012.
23.解:(1)设点B的坐标为(x,y).
∵B的“2级关联点”是B'(3,3),
∴解得∴点B的坐标为(1,1).
(2)∵M(m-1,2m)的“-3级关联点”N的坐标为(-m+3,-5m-1),且点N在y轴上,
∴-m+3=0,解得m=3.
∴-5m-1=-16.
∴点N的坐标为(0,-16).
24.解:(1)3
(2)
(3)点A'(x',y')能在△OCB的直角边上.∵A(0,2),A'(x',y'),∴x'=x+m=m,y'=y-2m=2-2m.∴点A'的坐标为(m,2-2m).若点A'在边OC上,则2-2m=0,解得m=1,此时点A'的坐标为(1,0).∵C(4,0),∴当m=1时,点A'在边OC上.若点A'在边BC上,则m=4,此时点A'的坐标为(4,-6),在第四象限,∴当m=4时,点A'不在边BC上.
综上所述,当m=1时,点A'(x',y')在△OCB的直角边上.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
1.根据下列表述,能确定位置的是 ( )
A.兴庆路
B.负二层停车场
C.太平洋影城3号厅2排
D.东经106°,北纬32°
2.(2024邯郸广平县月考)在平面直角坐标系中,点P(x,y)在第二象限,且点P到x轴和y轴的距离分别是3和4,则点P的坐标为( )
A.(4,-3) B.(-3,4)
C.(3,-4) D.(-4,3)
3.某小区的圆形花园中间有两条互相垂直的小路,园丁在花园中栽种了8棵桂花,如图所示.若A,B两处桂花的位置关于小路对称,在分别以两条小路为x,y轴的平面直角坐标系内,若点A的坐标为(-6,2),则点B的坐标为 ( )
A.(6,2) B.(-6,-2)
C.(2,6) D.(2,-6)
4.如图,在长方形ABCD中,A(-3,2),B(3,2),C(3,-1),则点D的坐标为 ( )
A.(-2,-1) B.(4,-1)
C.(-3,-2) D.(-3,-1)
5.(2024甘肃中考)敦煌文书是华夏民族引以为傲的艺术瑰宝,其中敦煌《算经》中出现的《田积表》部分如图1所示,它以表格形式将长方形土地的面积直观展示,可迅速准确地查出边长10步到60步的长方形田地面积,极大地提高了农田面积的测量效率.如图2是复原的部分《田积表》,表中对田地的长和宽都用步来表示,A区域表示的是长15步、宽16步的田地面积为一亩,用有序数对记为(15,16),那么有序数对记为(12,17)对应的田地面积为 ( )
A.一亩八十步 B.一亩二十步
C.半亩七十八步 D.半亩八十四步
6.已知点A(a-2,a+1),点B(2,3),直线AB∥x轴,则a的值是 ( )
A.1 B.2 C.3 D.4
7.已知A(a,-2)和B(4,b)关于原点对称,则a-b的值为 ( )
A.6 B.-6 C.2 D.-4
8.将线段AB在平面直角坐标系中平移,已知点A(-2,2),B(0,0),将线段平移后,其两个端点的对应点分别为A'(-1,4),B'(1,2),则它的平移情况是 ( )
A.向左平移了1个单位长度,向上平移了2个单位长度
B.向右平移了1个单位长度,向下平移了2个单位长度
C.向右平移了1个单位长度,向上平移了2个单位长度
D.向左平移了1个单位长度,向下平移了2个单位长度
9.已知点P(2-a,3a+6)到两坐标轴的距离相等,则点P的坐标是 ( )
A.(3,3) B.(3,-3)
C.(6,-6) D.(3,3)或(6,-6)
10.如果一个图形上各点的横坐标保持不变,而纵坐标分别都变为原来的,那么所得的图形与原图形相比 ( )
A.形状不变,图形缩小为原来的一半
B.形状不变,图形放大为原来的2倍
C.整个图形被横向压缩为原来的一半
D.整个图形被纵向压缩为原来的一半
11.如图,已知点A(-1,0),B(0,2),A与A'关于y轴对称,连接A'B,现将线段A'B以点A'为中心顺时针旋转90°得到A'B',则点B的对应点B'的坐标为 ( )
A.(3,1) B.(2,1)
C.(4,1) D.(3,2)
12.我们规定:在平面直角坐标系中,任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1-x2|+|y1-y2|.例如右图中,点M(-2,3)与点N(1,-1)之间的折线距离d(M,N)=|-2-1|+|3-(-1)|
=3+4=7.已知点P(-3,4),若点Q的坐标为(1,t),且d(P,Q)=8,则t的值为 ( )
A.0 B.-1
C.-1或7 D.0或8
二、填空题(本大题共4个小题,每小题3分,共12分)
13.已知点P在x轴上,且点P到y轴的距离等于6,则点P的坐标是 .
14.(2024邯郸永年区期末)“在生活的舞台上,我们都是不屈不挠的拳击手,面对无尽的挑战,挥洒汗水,拼搏向前!”2024年的春节档《热辣滚烫》展现了角色坚韧不拔的精神面貌.小明、小华、小亮三人也观看了此电影,如图是利用平面直角坐标系画出的影院内分布图,若分别以正东、正北方向为x轴、y轴的正方向,建立平面直角坐标系xOy,他们是这样描述自己的座位:
①小明:表示我座位的坐标为(-2,3);
②小华:在小明的座位向右走4个座位,再向上走2个座位,就可以找到我了;
③小亮:小旗帜所在的位置就是我的座位了.
则小亮座位的坐标为 .
15.如图,在平面直角坐标系中,将三角形ABC平移至三角形A1B1C1,P(a,b)是三角形ABC内一点,经平移后得到三角形A1B1C1内的对应点P1(a+8,b-5).若点A1的坐标为(5,-1),则点A的坐标为 .
16.如图,在平面直角坐标系中,A(6,0),B(0,y),连接AB,过点A作AC⊥AB.若AC=AB,x轴上的一点M(-1,0),连接CM,当点B在y轴上移动时,CM的最小值为 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)已知平面直角坐标系中有一点A(m-1,2m+3).
(1)点A在x轴上时,求点A的坐标.
(2)点A在第二、四象限的角平分线上时,求点A的坐标.
(3)点A到y轴的距离为2时,求点A的坐标.
18.(8分)下图中标明了李华同学家附近的一些地方的位置.
(1)根据图中所建立的平面直角坐标系,写出学校、邮局的坐标.
(2)某星期日早晨,李华同学从家里出发,沿着经过点(-2,-1),(-1,-2),(1,-2),(2,-1),(1,-1),(1,3),(-1,0),
(0,-1),(-2,-1)的路线转了一下,写出他经过的地方.
(3)顺次连接他在(2)中经过的地点,你能得到什么图形
19.(8分)如图,已知P(-2,4),M(-1,1),请根据每一问的要求作答:
(1)写出P关于y轴的对称点Q的坐标和M关于y轴的对称点N的坐标.
(2)写出P关于直线x=1的对称点R的坐标,并求PR的长.
(3)写出M关于x轴的对称点T的坐标,并求NT的长.
20.(8分)如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标.
(2)如果点P的坐标是(-a,0),其中0
(1)将△OAB向右平移1个单位长度后得到△O1A1B1,请画出△O1A1B1.
(2)将△O1A1B1各顶点的横、纵坐标都乘2,各对应顶点的坐标为O2 ,A2 ,B2 ;在直角坐标系中画出△O2A2B2.
(3)P(a,b)为△OAB内一点,则按题(1)(2)变换后点P在△O2A2B2中的对应点P'的坐标为 .
22.(10分)【观察·发现】如图,观察下列各点的排列规律:
A(0,1),A1(2,0),A2(3,2),A3(5,1),A4(6,3),….
【归纳·应用】
(1)点A6的坐标为 ;点A12的坐标为 .
(2)若点A2n的坐标为(3 036,1 013),求n的值.
23.(10分)在平面直角坐标系中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”,例如,点P(1,4)的“3级关联点”为Q(3×1+4,1+3×4),即Q(7,13).
(1)若点B的“2级关联点”是B'(3,3),求点B的坐标.
(2)已知点M(m-1,2m)的“-3级关联点”N位于y轴上,求点N的坐标.
24.(12分)在平面直角坐标系中,点A(x,y),点A'(x',y'),若x'=x+m,y'=y+n,即点A'(x+m,y+n),则表示A到点A'的一个平移.例如:点A(x,y),点A'(x',y'),若x'=x+1,y'=y-2,则表示点A向右平移1个单位长度,再向下平移2个单位长度得到点A'.
根据上述定义,探究下列问题:
(1)已知点A(x,y),A'(x-3,y),则线段AA'的长度是 .
(2)已知点A(x,y),A'(x+2,y-1),则线段AA'的长度是 .
(3)长方形AOCB在平面直角坐标系中的位置如图所示,A(0,2),C(4,0),点A'(x',y'),若x'=x+m,y'=
y-2m(m均为正数),点A'(x',y')能否在△OCB的直角边上 若能,求m的值,若不能,请说明理由.
【详解答案】
1.D
2.D 解析:∵点P(x,y)在第二象限,点P到x轴和y轴的距离分别是3和4,∴点P的横坐标是-4,纵坐标是3,即点P的坐标为(-4,3).故选D.
3.A 解析:由题意,得点B的坐标为(6,2).故选A.
4.D 解析:∵A(-3,2),B(3,2),∴AB=6,AB∥x轴.∵四边形ABCD是长方形,∴CD=AB=6,AB∥CD∥x轴.同理,AD∥BC∥y轴.∵C(3,-1),∴点D的坐标为(-3,-1).故选D.
5.D 解析:根据(15,16)对应的田地面积为一亩,可得(12,17)对应的田地面积是半亩八十四步.故选D.
6.B 解析:∵点A(a-2,a+1),点B(2,3),直线AB∥x轴,∴a+1=3.∴a=2.故选B.
7.B 解析:∵A(a,-2)和B(4,b)关于原点对称,∴a=-4,b=-(-2)=2.∴a-b=-4-2=-6.故选B.
8.C
9.D 解析:由题意,得|2-a|=|3a+6|,则2-a=3a+6或2-a=-3a-6,所以a=-1或a=-4.所以点P的坐标是(3,3)或(6,-6).故选D.
10.D 解析:∵横坐标不变,∴图形横向不变.∵纵坐标变为原来的,∴图形被纵向压缩为原来的一半.故选D.
11.A 解析:∵点A的坐标为(-1,0),点A'和点A关于y轴对称,∴点A'的坐标为(1,0).∴OA'=1.∵点B的坐标为(0,2),∴OB=2.如图,过点B'作x轴的垂线,垂足为M.由旋转可知,A'B=A'B',∠BA'B'=90°,∴∠BA'O+∠B'A'M=
∠BA'O+∠A'BO=90°,∴∠B'A'M=∠A'BO.在△A'BO和△B'A'M中,∴△A'BO≌△B'A'M(AAS).∴B'M=A'O=1,A'M=BO=2.∴OM=1+2=3.∴点B'的坐标为(3,1).故选A.
12.D 解析:∵P(-3,4),Q(1,t),d(P,Q)=8,∴|-3-1|+|4-t|=8,解得t=0或t=8.故选D.
13.(6,0)或(-6,0) 解析:∵点P在x轴上,且点P到y轴的距离等于6,∴xP=±6,yP=0.∴点P的坐标是(6,0)或(-6,0).
14.(2,0) 解析:∵小明座位的坐标为(-2,3),如图,建立平面直角坐标系.∴小华座位的坐标为(2,5).∵小旗帜位置的坐标为(2,0),即小亮座位的坐标为(2,0).
15.(-3,4)
16.6 解析:如图,过点C作CD⊥x轴于点D.∵∠ACD+∠CAD=∠CAD+∠BAO=90°,∴∠ACD=∠BAO.
∵∠ADC=∠BOA=90°,AC=BA,∴△ACD≌△BAO(AAS).∴CD=AO.∵A(6,0),∴CD=AO=6.∴点C在平行于x轴且与x轴距离为6的直线上运动,当MC垂直于这条直线时,CM最短,此时CM=CD=6.
17.解:(1)由题意,得2m+3=0,
解得m=-,故m-1=-,
所以点A的坐标为.
(2)由题意,得(m-1)+(2m+3)=0,
解得m=-,
故m-1=-,2m+3=,
所以点A的坐标为.
(3)由题意,得|m-1|=2,
解得m=3或m=-1,
故m-1=2,2m+3=9或m-1=-2,2m+3=1,
所以点A的坐标为(2,9)或(-2,1).
18.解:(1)学校(1,3),邮局(0,-1).
(2)李华家、商店、公园、汽车站、水果店、学校、娱乐城、邮局、李华家.
(3)得到的图形如图所示,像一只帆船.
19.解:(1)如图,点Q、点N即为所求,Q(2,4),N(1,1).
(2)如图,点R即为所求,R(4,4),PR=6.
(3)如图,点T即为所求.T(-1,-1),NT==2.
20.解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2).
(2)如图,当0
又∵P1与P2关于l:直线x=3对称,
设P2(x,0),可得=3,即x=6-a,∴P2(6-a,0).
∴PP2=6-a-(-a)=6-a+a=6.
21.解:(1)如图,△O1A1B1即为所求作三角形.
(2)(2,0) (4,4) (8,2)
如图,△O2A2B2即为所求作三角形.
(3)(2a+2,2b)
22.解:(1)(9,4) (18,7)
(2)A(0,1),A1(2,0),A2(3,2),A3(5,1),A4(6,3),…,
且A(0,1),A2(1×3,1+1),A4(2×3,1+2),A6(3×3,1+3),…,以此类推,
A2n,即A2n(3n,n+1),
∵点A2n的坐标为(3 036,1 013),
∴3n=3 036,解得n=1 012.
23.解:(1)设点B的坐标为(x,y).
∵B的“2级关联点”是B'(3,3),
∴解得∴点B的坐标为(1,1).
(2)∵M(m-1,2m)的“-3级关联点”N的坐标为(-m+3,-5m-1),且点N在y轴上,
∴-m+3=0,解得m=3.
∴-5m-1=-16.
∴点N的坐标为(0,-16).
24.解:(1)3
(2)
(3)点A'(x',y')能在△OCB的直角边上.∵A(0,2),A'(x',y'),∴x'=x+m=m,y'=y-2m=2-2m.∴点A'的坐标为(m,2-2m).若点A'在边OC上,则2-2m=0,解得m=1,此时点A'的坐标为(1,0).∵C(4,0),∴当m=1时,点A'在边OC上.若点A'在边BC上,则m=4,此时点A'的坐标为(4,-6),在第四象限,∴当m=4时,点A'不在边BC上.
综上所述,当m=1时,点A'(x',y')在△OCB的直角边上.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
