期中评估测试卷(含答案) 2024-2025学年数学冀教版八年级下册
文档属性
| 名称 | 期中评估测试卷(含答案) 2024-2025学年数学冀教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 591.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:42:03 | ||
图片预览


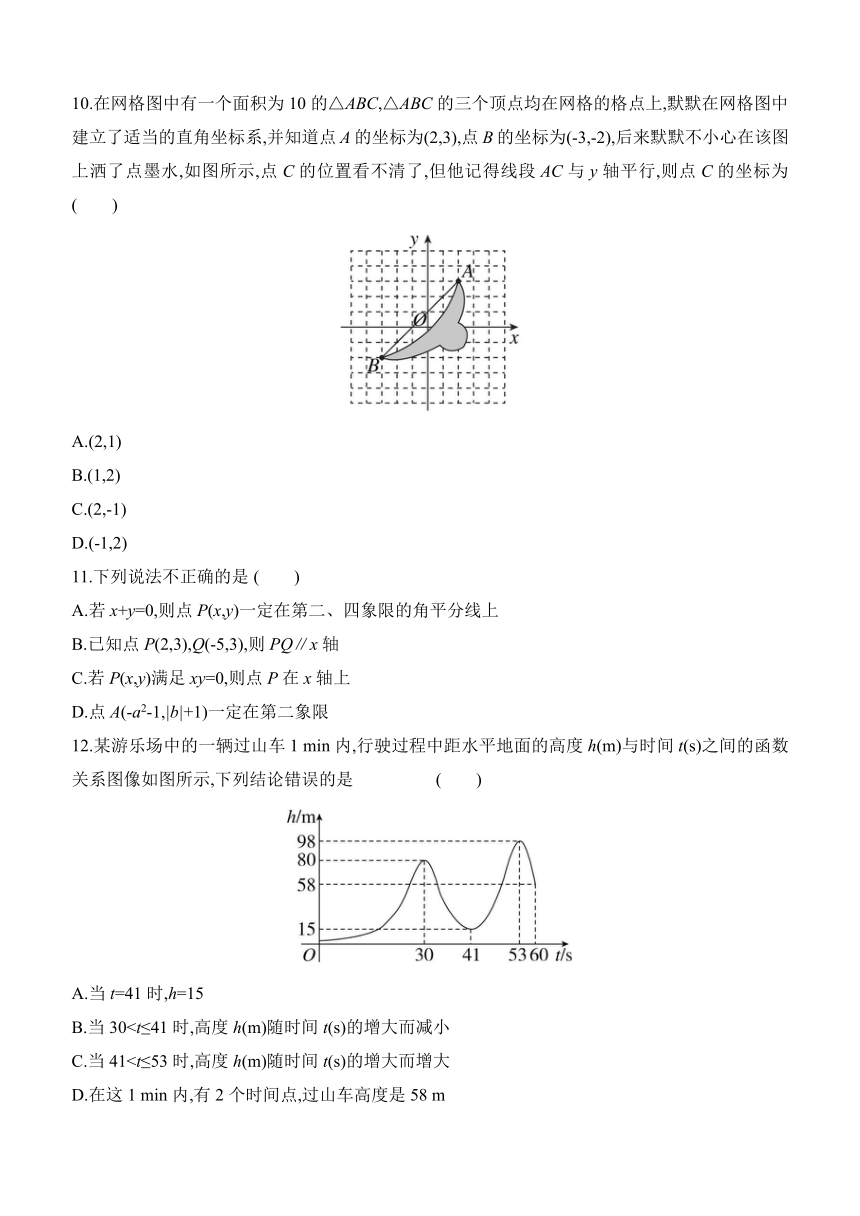
文档简介
期中评估测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024石家庄正定县期末)下列统计活动中,适合用问卷调查方法收集数据的是 ( )
①班级同学的身高;②某大学近五年的招生数;③学生对数学学科教师的满意程度;④1 h内某路口通过的车辆数.
A.①② B.②③ C.①③ D.③④
2.从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大.这个问题中自变量是 ( )
A.物体 B.速度 C.时间 D.空气
3.某区共有1万名学生参加数学考试,现从中抽取600名考生的数学成绩进行统计分析,以下说法正确的是 ( )
A.这是一次成绩普查
B.1万名考生是总体
C.每名考生的数学成绩是个体
D.600名考生是总体的一个样本
4.某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图所示的频数分布直方图,则下列说法不正确的是 ( )
A.抽取的学生共有50人
B.50.5至60.5这一分数段的频率为0.08
C.估计优秀率(80分以上为优秀)在36%左右
D.60.5至70.5这一分数段的频数为12
5.(2024广元中考)如果单项式-x2my3与单项式2x4y2-n的和仍是一个单项式,则在平面直角坐标系中点(m,n)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.点P(3,4)关于x轴对称的点为P1,点P1关于y轴对称的点为P2,则点P2的坐标为 ( )
A.(-3,4) B.(-3,-4) C.(3,-4) D.(4,3)
7.(2024廊坊香河县期中)如图,小明将写有“知”“识”“拓”“展”的四张卡片分别放入平面直角坐标系中,则写有“拓”的卡片遮住的点的坐标可能是 ( )
A.(-5,-3) B.(-5,3) C.(5,-3) D.(5,3)
8.云南某中学为了进一步落实初中学生学业水平考试美术科目赋分制度,决定在本学期继续开展(A.绘画,B.书法,C.剪纸,D.平面设计)四个类型的美术作品展示活动,学校从全校初中学生中抽取部分学生进行抽样调查,并根据调查结果绘制出如图所示的两幅不完整的统计图,则下列说法正确的是 ( )
A.样本容量为400
B.类型D的人数为80名
C.类型C所对应的扇形的圆心角度数为120°
D.若该校共有初中学生1 200名,则该校选择类型B的学生大约有350名
9.如图1,在△ABC中,CA=CB,直线l经过点A且垂直于AB.现将直线l以1 cm/s的速度向右匀速平移,直至到达点B时停止运动,直线l与边AB交于点M,与边AC(或CB)交于点N.设直线l移动的时间是x(s),△AMN的面积为y(cm2).若y关于x的函数图像如图2所示,则△ABC的周长为 ( )
A.16 cm B.17 cm C.18 cm D.20 cm
10.在网格图中有一个面积为10的△ABC,△ABC的三个顶点均在网格的格点上,默默在网格图中建立了适当的直角坐标系,并知道点A的坐标为(2,3),点B的坐标为(-3,-2),后来默默不小心在该图上洒了点墨水,如图所示,点C的位置看不清了,但他记得线段AC与y轴平行,则点C的坐标为 ( )
A.(2,1)
B.(1,2)
C.(2,-1)
D.(-1,2)
11.下列说法不正确的是 ( )
A.若x+y=0,则点P(x,y)一定在第二、四象限的角平分线上
B.已知点P(2,3),Q(-5,3),则PQ∥x轴
C.若P(x,y)满足xy=0,则点P在x轴上
D.点A(-a2-1,|b|+1)一定在第二象限
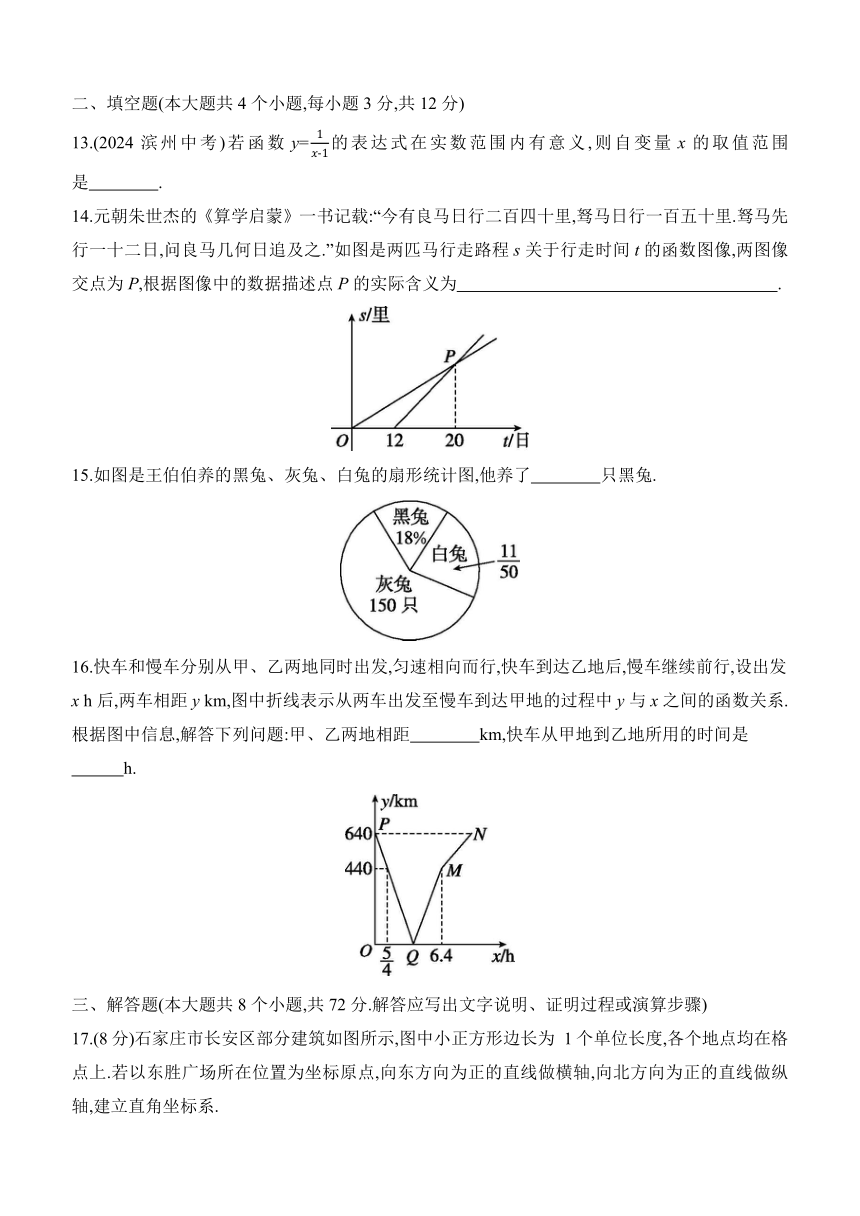
12.某游乐场中的一辆过山车1 min内,行驶过程中距水平地面的高度h(m)与时间t(s)之间的函数关系图像如图所示,下列结论错误的是 ( )
A.当t=41时,h=15
B.当30C.当41D.在这1 min内,有2个时间点,过山车高度是58 m
二、填空题(本大题共4个小题,每小题3分,共12分)
13.(2024滨州中考)若函数y=的表达式在实数范围内有意义,则自变量x的取值范围是 .
14.元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s关于行走时间t的函数图像,两图像交点为P,根据图像中的数据描述点P的实际含义为 .
15.如图是王伯伯养的黑兔、灰兔、白兔的扇形统计图,他养了 只黑兔.
16.快车和慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后,慢车继续前行,设出发x h后,两车相距y km,图中折线表示从两车出发至慢车到达甲地的过程中y与x之间的函数关系.根据图中信息,解答下列问题:甲、乙两地相距 km,快车从甲地到乙地所用的时间是
h.
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)石家庄市长安区部分建筑如图所示,图中小正方形边长为 1个单位长度,各个地点均在格点上.若以东胜广场所在位置为坐标原点,向东方向为正的直线做横轴,向北方向为正的直线做纵轴,建立直角坐标系.
(1)在图中画出平面直角坐标系.
(2)除“东胜广场”外,分别写出其他各场所的坐标.
18.(8分)某剧院的观众席的座位设置呈扇形,且按下面方式设置:
排数(x) 1 2 3 4 …
座位数(y) 50 53 56 59 …
(1)按照上表所示的规律,当x每增加1时,y如何变化
(2)写出座位数y与排数x之间的函数关系式.
(3)按照如表所示的规律,某一排可能有90个座位吗 说说你的理由.
19.(8分)(2024邯郸广平县月考)来自某商场财务部的报告表明,商场去年1—5月份的销售总额一共是370万元,图1、图2反映的是商场去年1—5月份的月销售总额和服装部各月销售额占比
情况.
(1)去年1—5月份,服装部各月销售额在商场当月销售总额中的占比最高的是 月份.
(2)求商场4月份的销售总额,并求服装部该月的销售额.
(3)某员工认为服装部5月份的销售额比4月份减少了,你认为正确吗 请说明理由.
20.(8分)已知A(-1,0),C(1,4),点B在x轴正半轴上,且AB=4.
(1)在如图所示的直角坐标系中画出△ABC.
(2)若将△ABC平移后点A的对应点A'的坐标为(-3,2),则点C的对应点C'的坐标为 .
(3)若在y轴上存在点P,使以A,B,P三点为顶点的三角形的面积为12,求点P的坐标.
21.(8分)(2024保定月考)某校八年级学生去参观纪念馆,为了解学生如何去的问题,班委对全体学生进行了调查,并将调查结果制成了条形统计图和扇形统计图(均不完整).
(1)该校八年级共有多少名学生
(2)采用“其他”方式出行的人数是骑自行车人数的 %.
(3)将条形统计图补充完整.
22.(10分)早晨,小欣与妈妈同时从家里出发,分别步行与骑自行车到在同一直线上且方向相反的两地上学与上班,如图是他们离家的距离y(m)与时间t(min)的函数图像.妈妈骑车走了10 min时接到小欣的电话,即以原速骑车前往小欣学校,并与小欣同时到达学校.已知小欣步行的速度为每分钟50 m,求小欣家与学校的距离及小欣早晨上学需要的时间.
23.(10分)一辆货车和一辆轿车先后从甲地前往乙地.如图,线段OB表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,线段CA表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系.
(1)货车的速度是 km/h.
(2)当1≤x≤5时,轿车离甲地的距离y(km)与时间x(h)之间的函数关系式为 .
(3)轿车出发多少小时能追上货车
(4)当轿车与甲地相距240 km时,货车与甲地相距多少千米
24.(12分)小平在学习过程中遇到一个函数y=+x.下面是小平对其研究的过程,请补充完整:
(1)函数y=+x的自变量x的取值范围是 .
(2)下表是y与x的几组对应值.
x … -2 -1 0 1 1.5 1.8 2.2 2.5 3 4 5 6 …
y … -1.75 -0.67 0.5 2 3.5 6.8 7.2 4.5 m 4.5 5.33 6.25 …
其中m的值为 .
(3)①根据表格中的数据,在平面直角坐标系xOy中,画出函数图像;
②过点(0,n)作平行于x轴的直线l,结合图像解决问题:若直线l与函数y=+x的图像有三个交点,则n的取值范围是 .
【详解答案】
1.C 解析:①班级同学的身高适合问卷调查;②某大学近五年的招生数,直接询问有关人员即可;③学生对数学学科教师的满意程度适合问卷调查;④1 h内某路口通过的车辆数可通过实际检测得到.故选C.
2.C 解析:因为速度随时间的变化而变化,所以时间是自变量.故选C.
3.C 解析:A.这是一次成绩抽样调查,故本选项不合题意;B.1万名考生的数学成绩是总体,故本选项不合题意;C.每名考生的数学成绩是个体,故本选项符合题意;D.600名考生的数学成绩是总体的一个样本,故本选项不合题意.故选C.
4.D 解析:抽取的学生共有4+10+18+12+6=50(人),故选项A正确;50.5至60.5这一分数段的频率为4÷50=0.08,故选项B正确;优秀率(80分以上为优秀)为×100%=36%,故选项C正确;60.5至70.5这一分数段的频数为10,故选项D错误.故选D.
5.D 解析:因为单项式-x2my3与单项式2x4y2-n的和仍是一个单项式,所以2m=4,2-n=3,解得m=2,n=-1,所以点(2,
-1)所在的象限为第四象限.故选D.
6.B 解析:点P(3,4)关于x轴对称的点为P1(3,-4),点P1关于y轴对称的点为P2(-3,-4).故选B.
7.C 解析:由题图可知,写有“拓”的卡片在第四象限,所以遮住的点的坐标可能是(5,-3).故选C.
8.A 解析:∵100÷25%=400(名),∴样本容量为400,故A正确;类型D的人数是400×10%=40(名),故B错误;
∵140÷400×100%=35%,∴类型C所占百分比为35%,360°×35%=126°,∴类型C所对应的扇形的圆心角度数为126°,故C错误;∵类型B的人数为400-100-140-40=120(名),该校共有初中学生1 200名,∴该校选择类型B的学生大约有1 200×=360(名).故D错误.故选A.
9.C 解析:依题意,得直线l运动到点B停止,且当直线l运动到点C时,△AMN的面积最大,∴AB=8 cm,且当AM=4 cm时,S△AMN=6 cm2.∵l⊥AB,∴S△AMN=AM·MN.∴AM=4 cm时,MN=MC=3 cm.在Rt△AMC中,CA==5(cm).∵CA=CB,∴C△ABC=CA+CB+AB=5+5+8=18(cm).故选C.
10.C 解析:∵A(2,3),B(-3,-2),线段AC与y轴平行,∴点B到AC的距离为2+3=5,∴S△ABC=AC·5=10,解得AC=4,∴点C的纵坐标为3-4=-1,∴点C的坐标为(2,-1).故选C.
11.C 解析:A.若x+y=0,则x,y互为相反数,点P(x,y)一定在第二、四象限的角平分线上,原说法正确,故此选项不符合题意;B.∵点P,Q的纵坐标相等,∴PQ∥x轴,原说法正确,故此选项不符合题意;C.若P(x,y)满足xy=0,则点P在x轴或y轴上,原说法不正确,故此选项符合题意;D.∵-a2-1<0,|b|+1>0,∴点A(-a2-1,|b|+1)一定在第二象限,原说法正确,故此选项不符合题意.故选C.
12.D 解析:A.当t=41时,h=15,故本选项正确;B.当3013.x≠1
14.20日时两匹马相遇
15.45 解析:由题图可知灰兔的百分比=100%-18%-×100%=60%,∴黑兔的数量=×18%=45(只).
16.640 6.4 解析:根据题意,得甲、乙两地相距640 km,快车从甲地到乙地所用的时间是6.4 h.
17.解:(1)建立平面直角坐标系,如图所示:
(2)结合(1)中的直角坐标系有北师附(0,4),钢厂(4,3),乐城半岛(-3,2),建华商场(-5,0),长安万达(3,0),中方商务(-3,
-2),建明小学(3,-2),22中(0,-3).
18.解:(1)由题表中数据可知,当x每增加1时,y增加3.
(2)由题意可得,y=50+3(x-1)=3x+47.
(3)某一排不可能有90个座位.
理由如下:若y=90,则3x+47=90,解得x=.
此时x不是整数,故某一排不可能有90个座位.
19.解:(1)1
(2)商场4月份的销售总额为370-90-85-60-70=65(万元),服装部该月的销售额为65×16%=10.4(万元).
(3)不正确.
理由:服装部4月份的销售额为10.4万元,5月份的销售额为70×15%=10.5(万元).
∵10.5万元>10.4万元,
∴该说法不正确.
20.解:(1)∵A(-1,0),点B在x轴正半轴上,且AB=4,∴B(3,0).
如图所示,△ABC即为所求.
(2)(-1,6)
解析:∵将△ABC平移后点A的对应点A'的坐标为(-3,2),如图,
∴平移方式为向上平移2个单位长度,向左平移2个单位长度.
∵C(1,4),
∴点C的对应点C'的坐标为(-1,6).
(3)设P(0,m),
则有×4×|m|=12.
∴m=±6.
∴点P的坐标为(0,6)或(0,-6).
21.解:(1)该校八年级共有的学生人数为50÷10%=500(名).
(2)50
(3)如图.
22.解:由题图,知妈妈骑车的速度为
2 500÷10=250(m/min).
设小欣家与学校的距离为y m.
根据题意,得+10,
解得y=1 250.
=25 (min).
答:小欣家与学校的距离为1 250 m,小欣早晨上学需要的时间为25 min.
23.解:(1)60
(2)y=90x-90
(3)设轿车出发t h能追上货车,
由题意得,60(t+1)=90t,
解得t=2.
答:轿车出发2 h能追上货车.
(4)当y=90x-90=240时,x=,
×60=220(km).
答:当轿车与甲地相距240 km时,货车与甲地相距220 km.
24.解:(1)x≠2
(2)4
(3)①连线,如图.
②n>4
解析:观察函数图像可知,在n=4时,直线y=4与函数y=+x的图像有两个交点,在n>4时,有三个交点.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024石家庄正定县期末)下列统计活动中,适合用问卷调查方法收集数据的是 ( )
①班级同学的身高;②某大学近五年的招生数;③学生对数学学科教师的满意程度;④1 h内某路口通过的车辆数.
A.①② B.②③ C.①③ D.③④
2.从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大.这个问题中自变量是 ( )
A.物体 B.速度 C.时间 D.空气
3.某区共有1万名学生参加数学考试,现从中抽取600名考生的数学成绩进行统计分析,以下说法正确的是 ( )
A.这是一次成绩普查
B.1万名考生是总体
C.每名考生的数学成绩是个体
D.600名考生是总体的一个样本
4.某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图所示的频数分布直方图,则下列说法不正确的是 ( )
A.抽取的学生共有50人
B.50.5至60.5这一分数段的频率为0.08
C.估计优秀率(80分以上为优秀)在36%左右
D.60.5至70.5这一分数段的频数为12
5.(2024广元中考)如果单项式-x2my3与单项式2x4y2-n的和仍是一个单项式,则在平面直角坐标系中点(m,n)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.点P(3,4)关于x轴对称的点为P1,点P1关于y轴对称的点为P2,则点P2的坐标为 ( )
A.(-3,4) B.(-3,-4) C.(3,-4) D.(4,3)
7.(2024廊坊香河县期中)如图,小明将写有“知”“识”“拓”“展”的四张卡片分别放入平面直角坐标系中,则写有“拓”的卡片遮住的点的坐标可能是 ( )
A.(-5,-3) B.(-5,3) C.(5,-3) D.(5,3)
8.云南某中学为了进一步落实初中学生学业水平考试美术科目赋分制度,决定在本学期继续开展(A.绘画,B.书法,C.剪纸,D.平面设计)四个类型的美术作品展示活动,学校从全校初中学生中抽取部分学生进行抽样调查,并根据调查结果绘制出如图所示的两幅不完整的统计图,则下列说法正确的是 ( )
A.样本容量为400
B.类型D的人数为80名
C.类型C所对应的扇形的圆心角度数为120°
D.若该校共有初中学生1 200名,则该校选择类型B的学生大约有350名
9.如图1,在△ABC中,CA=CB,直线l经过点A且垂直于AB.现将直线l以1 cm/s的速度向右匀速平移,直至到达点B时停止运动,直线l与边AB交于点M,与边AC(或CB)交于点N.设直线l移动的时间是x(s),△AMN的面积为y(cm2).若y关于x的函数图像如图2所示,则△ABC的周长为 ( )
A.16 cm B.17 cm C.18 cm D.20 cm
10.在网格图中有一个面积为10的△ABC,△ABC的三个顶点均在网格的格点上,默默在网格图中建立了适当的直角坐标系,并知道点A的坐标为(2,3),点B的坐标为(-3,-2),后来默默不小心在该图上洒了点墨水,如图所示,点C的位置看不清了,但他记得线段AC与y轴平行,则点C的坐标为 ( )
A.(2,1)
B.(1,2)
C.(2,-1)
D.(-1,2)
11.下列说法不正确的是 ( )
A.若x+y=0,则点P(x,y)一定在第二、四象限的角平分线上
B.已知点P(2,3),Q(-5,3),则PQ∥x轴
C.若P(x,y)满足xy=0,则点P在x轴上
D.点A(-a2-1,|b|+1)一定在第二象限
12.某游乐场中的一辆过山车1 min内,行驶过程中距水平地面的高度h(m)与时间t(s)之间的函数关系图像如图所示,下列结论错误的是 ( )
A.当t=41时,h=15
B.当30
二、填空题(本大题共4个小题,每小题3分,共12分)
13.(2024滨州中考)若函数y=的表达式在实数范围内有意义,则自变量x的取值范围是 .
14.元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s关于行走时间t的函数图像,两图像交点为P,根据图像中的数据描述点P的实际含义为 .
15.如图是王伯伯养的黑兔、灰兔、白兔的扇形统计图,他养了 只黑兔.
16.快车和慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后,慢车继续前行,设出发x h后,两车相距y km,图中折线表示从两车出发至慢车到达甲地的过程中y与x之间的函数关系.根据图中信息,解答下列问题:甲、乙两地相距 km,快车从甲地到乙地所用的时间是
h.
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)石家庄市长安区部分建筑如图所示,图中小正方形边长为 1个单位长度,各个地点均在格点上.若以东胜广场所在位置为坐标原点,向东方向为正的直线做横轴,向北方向为正的直线做纵轴,建立直角坐标系.
(1)在图中画出平面直角坐标系.
(2)除“东胜广场”外,分别写出其他各场所的坐标.
18.(8分)某剧院的观众席的座位设置呈扇形,且按下面方式设置:
排数(x) 1 2 3 4 …
座位数(y) 50 53 56 59 …
(1)按照上表所示的规律,当x每增加1时,y如何变化
(2)写出座位数y与排数x之间的函数关系式.
(3)按照如表所示的规律,某一排可能有90个座位吗 说说你的理由.
19.(8分)(2024邯郸广平县月考)来自某商场财务部的报告表明,商场去年1—5月份的销售总额一共是370万元,图1、图2反映的是商场去年1—5月份的月销售总额和服装部各月销售额占比
情况.
(1)去年1—5月份,服装部各月销售额在商场当月销售总额中的占比最高的是 月份.
(2)求商场4月份的销售总额,并求服装部该月的销售额.
(3)某员工认为服装部5月份的销售额比4月份减少了,你认为正确吗 请说明理由.
20.(8分)已知A(-1,0),C(1,4),点B在x轴正半轴上,且AB=4.
(1)在如图所示的直角坐标系中画出△ABC.
(2)若将△ABC平移后点A的对应点A'的坐标为(-3,2),则点C的对应点C'的坐标为 .
(3)若在y轴上存在点P,使以A,B,P三点为顶点的三角形的面积为12,求点P的坐标.
21.(8分)(2024保定月考)某校八年级学生去参观纪念馆,为了解学生如何去的问题,班委对全体学生进行了调查,并将调查结果制成了条形统计图和扇形统计图(均不完整).
(1)该校八年级共有多少名学生
(2)采用“其他”方式出行的人数是骑自行车人数的 %.
(3)将条形统计图补充完整.
22.(10分)早晨,小欣与妈妈同时从家里出发,分别步行与骑自行车到在同一直线上且方向相反的两地上学与上班,如图是他们离家的距离y(m)与时间t(min)的函数图像.妈妈骑车走了10 min时接到小欣的电话,即以原速骑车前往小欣学校,并与小欣同时到达学校.已知小欣步行的速度为每分钟50 m,求小欣家与学校的距离及小欣早晨上学需要的时间.
23.(10分)一辆货车和一辆轿车先后从甲地前往乙地.如图,线段OB表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,线段CA表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系.
(1)货车的速度是 km/h.
(2)当1≤x≤5时,轿车离甲地的距离y(km)与时间x(h)之间的函数关系式为 .
(3)轿车出发多少小时能追上货车
(4)当轿车与甲地相距240 km时,货车与甲地相距多少千米
24.(12分)小平在学习过程中遇到一个函数y=+x.下面是小平对其研究的过程,请补充完整:
(1)函数y=+x的自变量x的取值范围是 .
(2)下表是y与x的几组对应值.
x … -2 -1 0 1 1.5 1.8 2.2 2.5 3 4 5 6 …
y … -1.75 -0.67 0.5 2 3.5 6.8 7.2 4.5 m 4.5 5.33 6.25 …
其中m的值为 .
(3)①根据表格中的数据,在平面直角坐标系xOy中,画出函数图像;
②过点(0,n)作平行于x轴的直线l,结合图像解决问题:若直线l与函数y=+x的图像有三个交点,则n的取值范围是 .
【详解答案】
1.C 解析:①班级同学的身高适合问卷调查;②某大学近五年的招生数,直接询问有关人员即可;③学生对数学学科教师的满意程度适合问卷调查;④1 h内某路口通过的车辆数可通过实际检测得到.故选C.
2.C 解析:因为速度随时间的变化而变化,所以时间是自变量.故选C.
3.C 解析:A.这是一次成绩抽样调查,故本选项不合题意;B.1万名考生的数学成绩是总体,故本选项不合题意;C.每名考生的数学成绩是个体,故本选项符合题意;D.600名考生的数学成绩是总体的一个样本,故本选项不合题意.故选C.
4.D 解析:抽取的学生共有4+10+18+12+6=50(人),故选项A正确;50.5至60.5这一分数段的频率为4÷50=0.08,故选项B正确;优秀率(80分以上为优秀)为×100%=36%,故选项C正确;60.5至70.5这一分数段的频数为10,故选项D错误.故选D.
5.D 解析:因为单项式-x2my3与单项式2x4y2-n的和仍是一个单项式,所以2m=4,2-n=3,解得m=2,n=-1,所以点(2,
-1)所在的象限为第四象限.故选D.
6.B 解析:点P(3,4)关于x轴对称的点为P1(3,-4),点P1关于y轴对称的点为P2(-3,-4).故选B.
7.C 解析:由题图可知,写有“拓”的卡片在第四象限,所以遮住的点的坐标可能是(5,-3).故选C.
8.A 解析:∵100÷25%=400(名),∴样本容量为400,故A正确;类型D的人数是400×10%=40(名),故B错误;
∵140÷400×100%=35%,∴类型C所占百分比为35%,360°×35%=126°,∴类型C所对应的扇形的圆心角度数为126°,故C错误;∵类型B的人数为400-100-140-40=120(名),该校共有初中学生1 200名,∴该校选择类型B的学生大约有1 200×=360(名).故D错误.故选A.
9.C 解析:依题意,得直线l运动到点B停止,且当直线l运动到点C时,△AMN的面积最大,∴AB=8 cm,且当AM=4 cm时,S△AMN=6 cm2.∵l⊥AB,∴S△AMN=AM·MN.∴AM=4 cm时,MN=MC=3 cm.在Rt△AMC中,CA==5(cm).∵CA=CB,∴C△ABC=CA+CB+AB=5+5+8=18(cm).故选C.
10.C 解析:∵A(2,3),B(-3,-2),线段AC与y轴平行,∴点B到AC的距离为2+3=5,∴S△ABC=AC·5=10,解得AC=4,∴点C的纵坐标为3-4=-1,∴点C的坐标为(2,-1).故选C.
11.C 解析:A.若x+y=0,则x,y互为相反数,点P(x,y)一定在第二、四象限的角平分线上,原说法正确,故此选项不符合题意;B.∵点P,Q的纵坐标相等,∴PQ∥x轴,原说法正确,故此选项不符合题意;C.若P(x,y)满足xy=0,则点P在x轴或y轴上,原说法不正确,故此选项符合题意;D.∵-a2-1<0,|b|+1>0,∴点A(-a2-1,|b|+1)一定在第二象限,原说法正确,故此选项不符合题意.故选C.
12.D 解析:A.当t=41时,h=15,故本选项正确;B.当30
14.20日时两匹马相遇
15.45 解析:由题图可知灰兔的百分比=100%-18%-×100%=60%,∴黑兔的数量=×18%=45(只).
16.640 6.4 解析:根据题意,得甲、乙两地相距640 km,快车从甲地到乙地所用的时间是6.4 h.
17.解:(1)建立平面直角坐标系,如图所示:
(2)结合(1)中的直角坐标系有北师附(0,4),钢厂(4,3),乐城半岛(-3,2),建华商场(-5,0),长安万达(3,0),中方商务(-3,
-2),建明小学(3,-2),22中(0,-3).
18.解:(1)由题表中数据可知,当x每增加1时,y增加3.
(2)由题意可得,y=50+3(x-1)=3x+47.
(3)某一排不可能有90个座位.
理由如下:若y=90,则3x+47=90,解得x=.
此时x不是整数,故某一排不可能有90个座位.
19.解:(1)1
(2)商场4月份的销售总额为370-90-85-60-70=65(万元),服装部该月的销售额为65×16%=10.4(万元).
(3)不正确.
理由:服装部4月份的销售额为10.4万元,5月份的销售额为70×15%=10.5(万元).
∵10.5万元>10.4万元,
∴该说法不正确.
20.解:(1)∵A(-1,0),点B在x轴正半轴上,且AB=4,∴B(3,0).
如图所示,△ABC即为所求.
(2)(-1,6)
解析:∵将△ABC平移后点A的对应点A'的坐标为(-3,2),如图,
∴平移方式为向上平移2个单位长度,向左平移2个单位长度.
∵C(1,4),
∴点C的对应点C'的坐标为(-1,6).
(3)设P(0,m),
则有×4×|m|=12.
∴m=±6.
∴点P的坐标为(0,6)或(0,-6).
21.解:(1)该校八年级共有的学生人数为50÷10%=500(名).
(2)50
(3)如图.
22.解:由题图,知妈妈骑车的速度为
2 500÷10=250(m/min).
设小欣家与学校的距离为y m.
根据题意,得+10,
解得y=1 250.
=25 (min).
答:小欣家与学校的距离为1 250 m,小欣早晨上学需要的时间为25 min.
23.解:(1)60
(2)y=90x-90
(3)设轿车出发t h能追上货车,
由题意得,60(t+1)=90t,
解得t=2.
答:轿车出发2 h能追上货车.
(4)当y=90x-90=240时,x=,
×60=220(km).
答:当轿车与甲地相距240 km时,货车与甲地相距220 km.
24.解:(1)x≠2
(2)4
(3)①连线,如图.
②n>4
解析:观察函数图像可知,在n=4时,直线y=4与函数y=+x的图像有两个交点,在n>4时,有三个交点.
同课章节目录
