期末评估测试卷(一) (含答案)2024-2025学年数学冀教版八年级下册
文档属性
| 名称 | 期末评估测试卷(一) (含答案)2024-2025学年数学冀教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 862.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:41:18 | ||
图片预览

文档简介
期末评估测试卷(一)
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
1.为了解某地区八年级学生的体质健康情况,从该地区13 000名八年级学生中随机抽取了1 000名学生进行体质健康情况调查,这次调查中的样本是 ( )
A.被抽取的1 000名学生的体质健康情况
B.被抽取的1 000名学生
C.该地区13 000名八年级学生
D.13 000名八年级学生的体质健康情况
2.正五边形的外角和为 ( )
A.180° B.360° C.540° D.720°
3.如图,MN⊥x轴,点M(-3,5),MN=3,则点N的坐标为 ( )
A.(-6,5) B.(-3,2)
C.(3,-2) D.(-3,3)
4.“五育”在基础教育中占着重要的地位和作用,其中,体育是增强学生体质、发展体力和运动能力,帮助学生养成锻炼身体和卫生习惯的教育.为加强体育锻炼,小明为自己制定每日的运动计划并做了记录,如图是小明某一周参加体育运动时间的折线统计图,下列说法错误的是( )
A.小明星期六参加体育运动的时间最少
B.小明星期四与星期六参加体育运动的时间之差为1 h
C.小明星期二参加体育运动的时长是60 min
D.小明星期四到星期日参加体育运动的时间越来越少
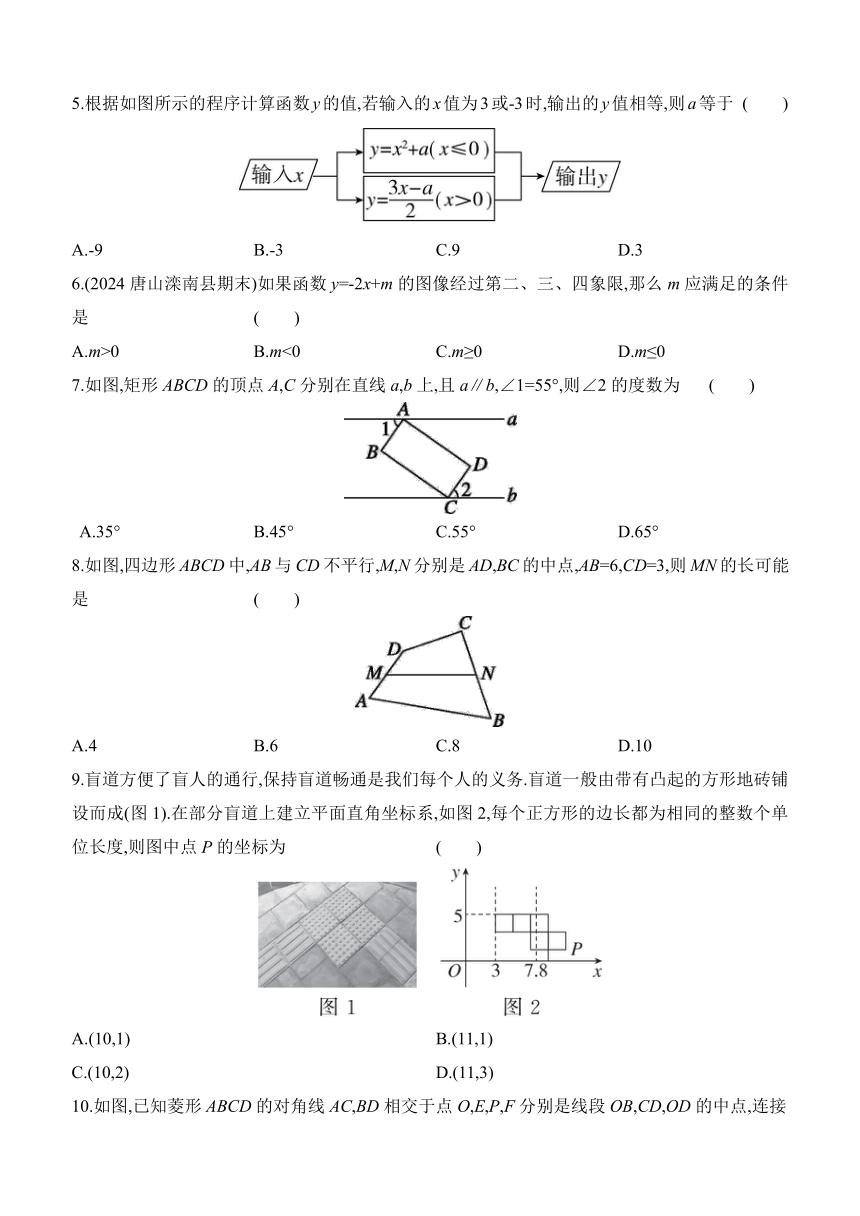
5.根据如图所示的程序计算函数y的值,若输入的x值为3或-3时,输出的y值相等,则a等于 ( )
A.-9 B.-3 C.9 D.3
6.(2024唐山滦南县期末)如果函数y=-2x+m的图像经过第二、三、四象限,那么m应满足的条件是 ( )
A.m>0 B.m<0 C.m≥0 D.m≤0
7.如图,矩形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=55°,则∠2的度数为 ( )
A.35° B.45° C.55° D.65°
8.如图,四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=6,CD=3,则MN的长可能是 ( )
A.4 B.6 C.8 D.10
9.盲道方便了盲人的通行,保持盲道畅通是我们每个人的义务.盲道一般由带有凸起的方形地砖铺设而成(图1).在部分盲道上建立平面直角坐标系,如图2,每个正方形的边长都为相同的整数个单位长度,则图中点P的坐标为 ( )
A.(10,1) B.(11,1)
C.(10,2) D.(11,3)
10.如图,已知菱形ABCD的对角线AC,BD相交于点O,E,P,F分别是线段OB,CD,OD的中点,连接EP,PF.若AC=8,PE=2,则菱形ABCD的面积为 ( )
A.64 B.48 C.24 D.16
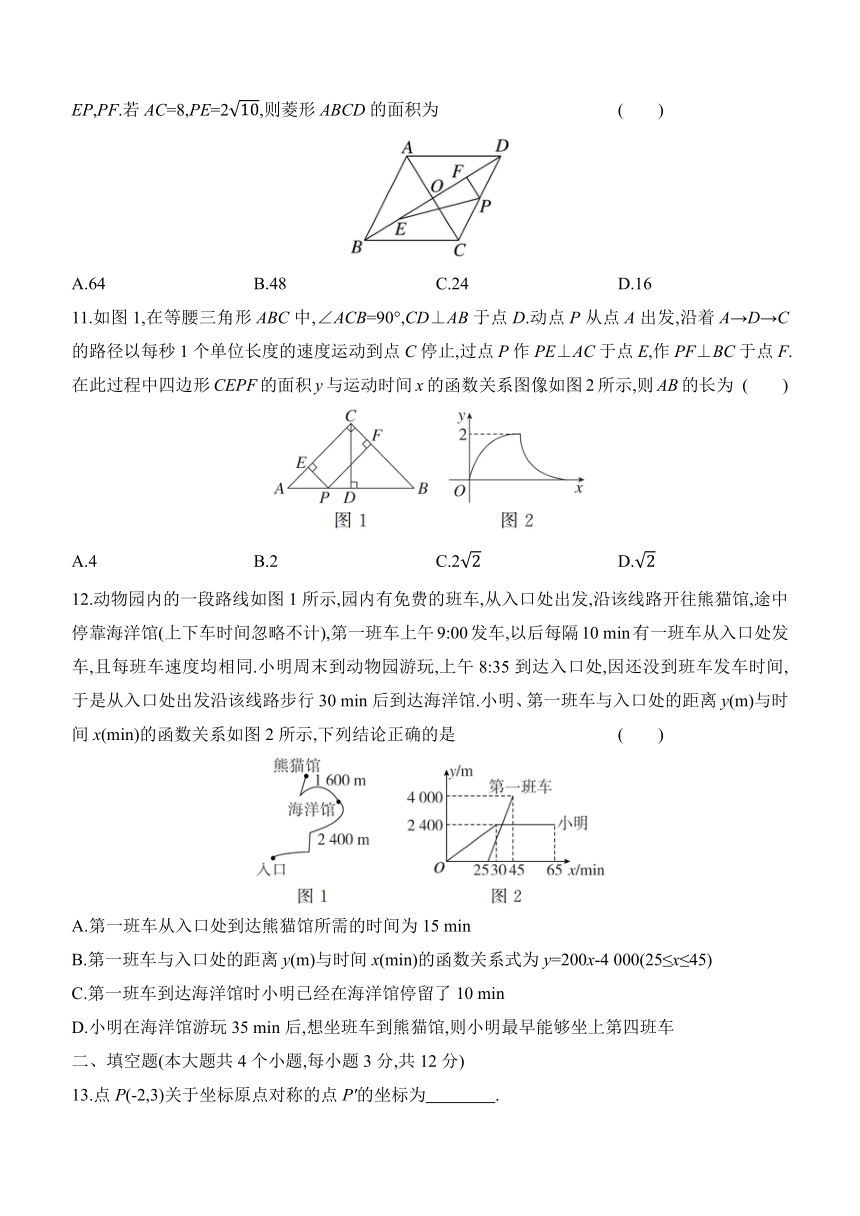
11.如图1,在等腰三角形ABC中,∠ACB=90°,CD⊥AB于点D.动点P从点A出发,沿着A→D→C的路径以每秒1个单位长度的速度运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于点F.在此过程中四边形CEPF的面积y与运动时间x的函数关系图像如图2所示,则AB的长为 ( )
A.4 B.2 C.2 D.
12.动物园内的一段路线如图1所示,园内有免费的班车,从入口处出发,沿该线路开往熊猫馆,途中停靠海洋馆(上下车时间忽略不计),第一班车上午9:00发车,以后每隔10 min有一班车从入口处发车,且每班车速度均相同.小明周末到动物园游玩,上午8:35到达入口处,因还没到班车发车时间,于是从入口处出发沿该线路步行30 min后到达海洋馆.小明、第一班车与入口处的距离y(m)与时间x(min)的函数关系如图2所示,下列结论正确的是 ( )
A.第一班车从入口处到达熊猫馆所需的时间为15 min
B.第一班车与入口处的距离y(m)与时间x(min)的函数关系式为y=200x-4 000(25≤x≤45)
C.第一班车到达海洋馆时小明已经在海洋馆停留了10 min
D.小明在海洋馆游玩35 min后,想坐班车到熊猫馆,则小明最早能够坐上第四班车
二、填空题(本大题共4个小题,每小题3分,共12分)
13.点P(-2,3)关于坐标原点对称的点P'的坐标为 .
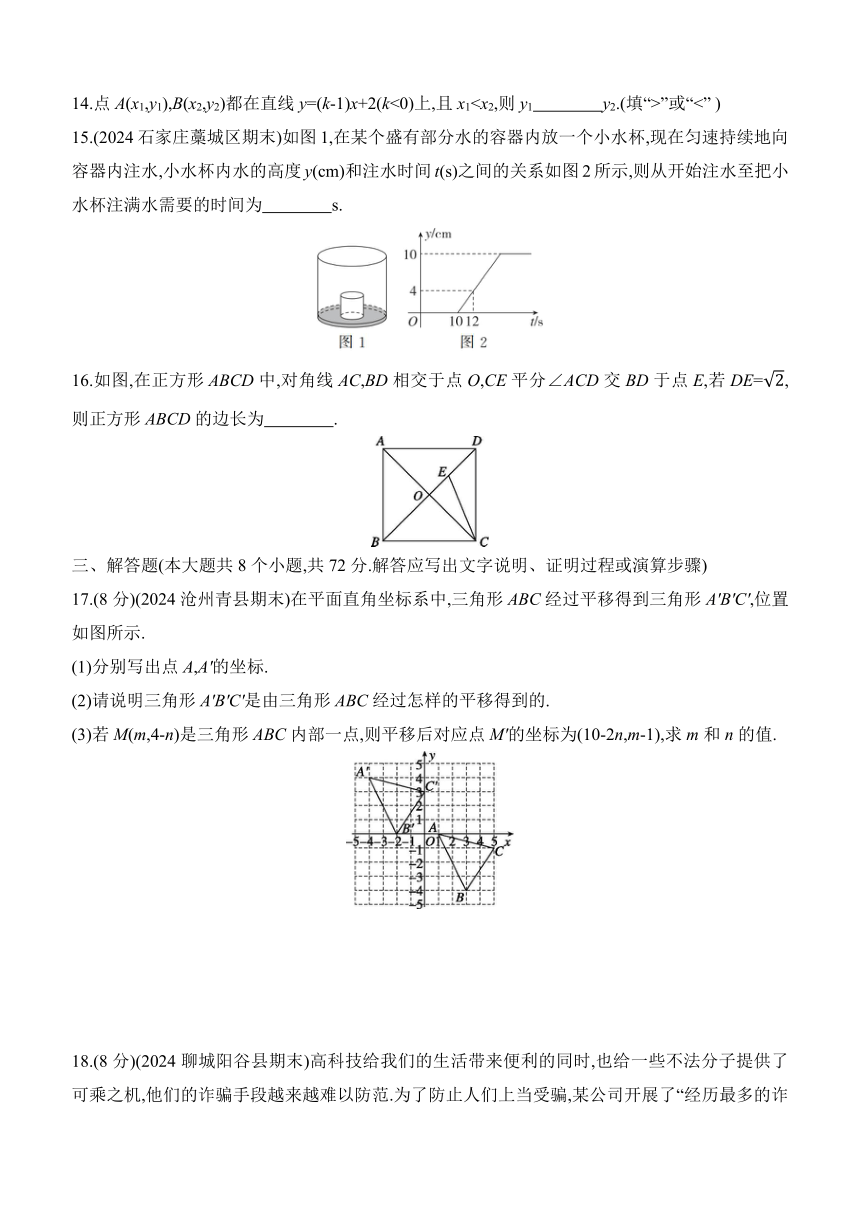
14.点A(x1,y1),B(x2,y2)都在直线y=(k-1)x+2(k<0)上,且x1”或“<” )
15.(2024石家庄藁城区期末)如图1,在某个盛有部分水的容器内放一个小水杯,现在匀速持续地向容器内注水,小水杯内水的高度y(cm)和注水时间t(s)之间的关系如图2所示,则从开始注水至把小水杯注满水需要的时间为 s.
16.如图,在正方形ABCD中,对角线AC,BD相交于点O,CE平分∠ACD交BD于点E,若DE=,则正方形ABCD的边长为 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)(2024沧州青县期末)在平面直角坐标系中,三角形ABC经过平移得到三角形A'B'C',位置如图所示.
(1)分别写出点A,A'的坐标.
(2)请说明三角形A'B'C'是由三角形ABC经过怎样的平移得到的.
(3)若M(m,4-n)是三角形ABC内部一点,则平移后对应点M'的坐标为(10-2n,m-1),求m和n的值.
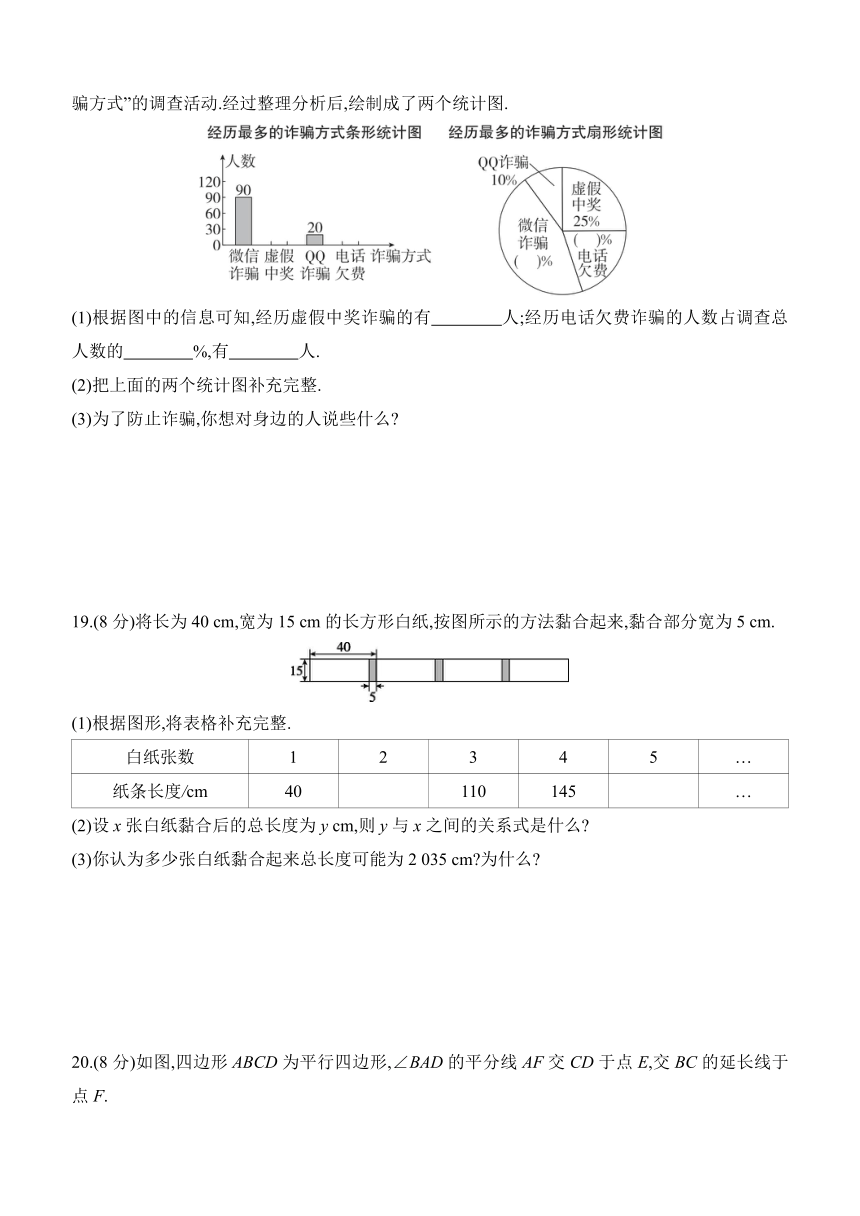
18.(8分)(2024聊城阳谷县期末)高科技给我们的生活带来便利的同时,也给一些不法分子提供了可乘之机,他们的诈骗手段越来越难以防范.为了防止人们上当受骗,某公司开展了“经历最多的诈骗方式”的调查活动.经过整理分析后,绘制成了两个统计图.
(1)根据图中的信息可知,经历虚假中奖诈骗的有 人;经历电话欠费诈骗的人数占调查总人数的 %,有 人.
(2)把上面的两个统计图补充完整.
(3)为了防止诈骗,你想对身边的人说些什么
19.(8分)将长为40 cm,宽为15 cm的长方形白纸,按图所示的方法黏合起来,黏合部分宽为5 cm.
(1)根据图形,将表格补充完整.
白纸张数 1 2 3 4 5 …
纸条长度/cm 40 110 145 …
(2)设x张白纸黏合后的总长度为y cm,则y与x之间的关系式是什么
(3)你认为多少张白纸黏合起来总长度可能为2 035 cm 为什么
20.(8分)如图,四边形ABCD为平行四边形,∠BAD的平分线AF交CD于点E,交BC的延长线于点F.
(1)求证:BF=CD.
(2)连接BE,若BE⊥AF,∠BFA=60°,AB=4,求平行四边形ABCD的面积.
21.(8分)在平面直角坐标系中,给出如下定义:点P到x轴、y轴的距离的较大值称为点P的“长距”,点Q到x轴、y轴的距离相等时,称Q为“完美点”.
(1)点A(-1,3)的“长距”为 .
(2)若B(4a-1,-3)是“完美点”,求a的值.
(3)若点C(-2,3b-2)的长距为4,且点C在第二象限内,点D的坐标为(9-2b,-5),试说明:D是“完美点”.
22.(10分)十一期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以上信息,解答下列问题:
(1)设租车时间为x h,租用甲公司的车每日所需费用为y1元,租用乙公司的车每日所需费用为y2元,分别求出y1,y2关于x的函数表达式.
(2)当租车时间为多少小时时,两种方案所需费用相同
(3)根据(2)的计算结果,结合图像,请你帮助小明选择怎样的出游方案更合算.
23.(10分)(2024莆田荔城区期中)在菱形ABCD中,∠ABC=60°,P是直线BD上一动点,以AP为边向右侧作等边三角形APE(A,P,E按逆时针排列),点E的位置随点P的位置变化而变化.
(1)如图1,当点P在线段BD上,且点E在菱形ABCD内部或边上时,连接CE,则BP与CE的数量关系是 ,BC与CE的位置关系是 .
(2)如图2,当点P在线段BD上,且点E在菱形ABCD外部时,(1)中的结论是否还成立 若成立,请予以证明;若不成立,请说明理由.
24.(12分)某同学利用平面镜成像原理设计了一个游戏,如图,在y轴上放置一平面镜,从点A(2,5)处向平面镜发射一束光(看成线),经反射后沿直线l:y=mx+n(m≠0)传播.
(1)写出点A在平面镜内的虚像A'的坐标.
(2)若反射光束经过x轴上的点(8,0),求直线l的函数表达式.
(3)在x轴上从左到右有两点C,D,且CD=1,从点D向上作DB⊥x轴,且BD=2.
①若使△BCD沿x轴左右平移,且保证沿(2)中直线l传播的光束能照射到边BC(包括端点)上,则点B横坐标的最大值比最小值大多少
②若使△BCD位置固定,且点C的坐标为(9,0),仍保证沿直线l传播的光束能照射到边BC(包括端点)上,直接写出m的取值范围.
【详解答案】
1.A 解析:为了解某地区八年级学生的体质健康情况,从该地区13 000名八年级学生中随机抽取了1 000名学生进行体质健康情况调查,这次调查中的样本是被抽取的1 000名学生的体质健康情况.故选A.
2.B 解析:任意多边形的外角和都是360°,故正五边形的外角和为360°.故选B.
3.B 解析:由题意,得将点M向下平移3个单位长度,纵坐标为5-3=2,∴N(-3,2).故选B.
4.D 解析:由折线统计图可知,小明星期六参加体育运动时间最少,故A正确,不符合题意;小明星期四与星期六参加体育运动时间之差为70-10=60(min)=1(h),故B正确,不符合题意;小明星期二参加体育运动的时长是60 min,故C正确,不符合题意;小明星期四到星期六参加体育运动时间越来越少,故D错误,符合题意.故选D.
5.B 解析:当x=-3时,y=9+a;当x=3时,y=.根据题意,得9+a=,解得a=-3.故选B.
6.B 解析:∵函数y=-2x+m的图像经过第二、三、四象限,∴m<0.故选B.
7.C 解析:如图,延长AB交直线b于点E.∵a∥b,∴∠AEC=∠1=55°.∵四边形ABCD是矩形,∴AB∥CD.∴∠2=∠AEC=55°.故选C.
8.A 解析:如图,连接BD,取BD的中点E,连接ME,NE.∵M是AD的中点,E是BD的中点,∴ME=AB=3.同理,NE=CD=1.5.在△MNE中,3-1.59.B 解析:设正方形的边长为x个单位长度.由题图可知,解得1.610.B 解析:∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD.∵E,P,F分别是线段OB,CD,OD的中点,
∴OE=EB,OF=DF,PF∥AC,PF=OC=AC=2.∴PF⊥BD,∴EF==6.∴BD=2EF=12.
∴菱形ABCD的面积=AC·BD=×8×12=48.故选B.
11.A 解析:当点P运动到点D处时,如图,∴四边形CEPF的面积为y=2.∵PE⊥AC,PF⊥BC,∠ACB=90°,∴四边形CEPF为矩形.∵AC=BC,∴∠ACD=∠BCD,AD=BD.∴DE=DF.∴矩形DECF为正方形.∴DE2=2.∴DE=.∵∠A=45°,∴AD=DE=2.∴AB=4.故选A.
12.D 解析:A.第一班车从入口处到达熊猫馆所需的时间为45-25=20(min),故选项A错误,不符合题意;B.设第一班车与入口处的距离y(m)与时间x(min)的函数关系式为y=kx+b.将(25,0),(45,4 000)分别代入,得解得∴y=200x-5 000(25≤x≤45).故选项B错误,不符合题意;C.当y=2 400时,200x-5 000=2 400,∴x=37,而小明到达海洋馆的时间x=30,∴第一班车到达海洋馆时小明已经在海洋馆停留了7 min,故选项C错误,不符合题意;D.小明上午8:35到达入口处,到达海洋馆的时间是9:05,在海洋馆游玩35 min后是9:40,而第三班车9:20从入口处发车,经过37-25=12(min),即9:32到达海洋馆,小明不能赶上,第四班车9:30从入口处发车,9:42到达海洋馆,小明能赶上,故选项D正确,符合题意.故选D.
13.(2,-3) 解析:根据关于原点对称的点,横坐标与纵坐标都互为相反数求解.
14.> 解析:∵k<0,∴k-1<-1.∴y随x的增大而减小.又∵点A(x1,y1),B(x1,y2)都在直线y=(k-1)x+2(k<0)上,且x1y2.
15.15 解析:设y与t的关系式为y=kt+b(k,b为常数,且k≠0).将坐标(10,0)和(12,4)代入y=kt+b,得解得∴y与t的关系式为y=2t-20(t≥10).当注满水杯时y=10,∴2t-20=10,解得t=15.
16.2+ 解析:如图,过点E作CD的垂线,垂足为M.∵四边形ABCD是正方形,∴∠ODC=45°,AC⊥BD,OD=OC.∴△DME是等腰直角三角形.又∵DE=,∴EM=1.∵CE平分∠ACD,EO⊥AC,EM⊥CD,∴EO=EM=1.∴OD= DE+OE=+1.∵△ODC是等腰直角三角形,∴DC=OD=2+.
17.解:(1)由题图可得A(1,0),A'(-4,4).
(2)三角形A'B'C'是由三角形ABC向左平移5个单位长度,向上平移4个单位长度得到的.
(3)由题意,得解得
18.解:(1)50 20 40
(2)1-10%-25%-20%=45%.
补全统计图如下:
(3)为了防止诈骗,我想对身边的人说:加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电.(答案不唯一).
19.解:(1)75 180
(2)根据题意和所给图形可得出:
y=40x-5(x-1)=35x+5,
∴y与x之间的关系式是y=35x+5.
(3)令y=2 035,得2 035=35x+5,
解得x=58.
∵x为整数,
∴58张白纸黏合,总长度为2 035 cm.
20.(1)证明:∵四边形ABCD为平行四边形,∴AB=CD,AD∥BC.
∴∠FAD=∠AFB.
又∵AF平分∠BAD,
∴∠FAD=∠FAB.
∴∠AFB=∠FAB.
∴AB=BF.∴BF=CD.
(2)解:∵∠F=60°,BF=AB=4,
∴△ABF是等边三角形.
∴∠ABF=60°.∴AF=AB=4.
∵BE⊥AF,
∴∠FBE=∠ABE=×60°=30°.
∴AE=EF=AF=2.
∴BE==2.
∴S△ABF=AF·BE=×4×2=4.
在△ADE和△FCE中,
∴△ADE≌△FCE(ASA).
∴S△ADE=S△FCE.
∴S△ADE+S四边形ABCE=S△FCE+S四边形ABCE,
即S平行四边形ABCD=S△ABF=4,
∴平行四边形ABCD的面积为4.
21.解:(1)3
(2)∵B(4a-1,-3)是“完美点”,
∴|4a-1|=|-3|.
∴4a-1=3或4a-1=-3,
解得a=1或a=-.
(3)∵点C(-2,3b-2)的长距为4,且点C在第二象限内,
∴3b-2=4,解得b=2.
∴9-2b=5.
∴点D的坐标为(5,-5).
∴D到x轴、y轴的距离都是5.
∴点D是“完美点”.
22.解:(1)设y1=k1x+80.
把点(1,95)代入,
可得95=k1+80,解得k1=15,
∴y1=15x+80(x≥0).
设y2=k2x.
把(1,30)代入,可得30=k2,即k2=30,∴y2=30x(x≥0).
(2)当y1=y2时,15x+80=30x,
解得x=.
∴当租车时间为 h时,两种方案所需费用相同.
(3)由(2)知,当y1=y2时,x=.
当y1>y2时,15x+80>30x,
解得x<;
当y1解得x>;
∴当租车时间为 h,任意选择其中的一个方案;当租车时间小于 h,选择方案二合算;当租车时间大于 h,选择方案一合算.
23.解:(1)BP=CE BC⊥CE
解析:如图1,连接AC,延长CE交AD于点H.
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°.
∴AB=AC,∠BAC=60°,∠CAH=60°.
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°.
∵∠BAC=∠PAE,
∴∠BAP+∠PAC=∠CAE+∠PAC.
∴∠BAP=∠CAE.
∴△BAP≌△CAE(SAS).
∴BP=CE,∠ABP=∠ACE=30°.
∵△ACD是等边三角形,
∴∠ACD=2∠ACH=60°.
∴CH⊥AD,即CE⊥AD.
又∵AD∥BC,∴BC⊥CE.
(2)(1)中结论仍然成立.证明如下:如图2,连接AC.
则△ABC,△ACD为等边三角形.
在△ABP和△ACE中,AB=AC,AP=AE,
又∵∠BAP=∠BAC+∠CAP=60°+∠CAP,∠CAE=∠EAP+∠CAP=60°+∠CAP,
∴∠BAP=∠CAE.
∴△ABP≌△ACE(SAS).
∴BP=CE,∠ACE=∠ABD=30°.
设CE与AD交于点H.
同理可得∠ACD=2∠ACH=60°,
∴CE⊥AD.
又∵AD∥BC,∴CE⊥BC.
24.解:(1)∵A(2,5),∴A'(-2,5).
(2)把x=-2,y=5和x=8,y=0代入y=mx+n,
得解得
∴直线l的函数表达式为y=-x+4.
(3)①如图1.
由(2),得直线l的函数表达式为y=-x+4,
当y=2时,得2=-x+4,解得x=4,
当y=0时,由(2)可知x=8,
∴点B横坐标的最大值比最小值大(8+1)-4=5.
②m的取值范围为-≤m≤-.
解法提示:如图2.
由题意可得C(9,0),D(10,0),B(10,2),
将C(9,0),A'(-2,5)代入y=mx+n,
得解得m=-.
将B(10,2),A'(-2,5)代入y=mx+n,
得解得m=-.
故-≤m≤-.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
1.为了解某地区八年级学生的体质健康情况,从该地区13 000名八年级学生中随机抽取了1 000名学生进行体质健康情况调查,这次调查中的样本是 ( )
A.被抽取的1 000名学生的体质健康情况
B.被抽取的1 000名学生
C.该地区13 000名八年级学生
D.13 000名八年级学生的体质健康情况
2.正五边形的外角和为 ( )
A.180° B.360° C.540° D.720°
3.如图,MN⊥x轴,点M(-3,5),MN=3,则点N的坐标为 ( )
A.(-6,5) B.(-3,2)
C.(3,-2) D.(-3,3)
4.“五育”在基础教育中占着重要的地位和作用,其中,体育是增强学生体质、发展体力和运动能力,帮助学生养成锻炼身体和卫生习惯的教育.为加强体育锻炼,小明为自己制定每日的运动计划并做了记录,如图是小明某一周参加体育运动时间的折线统计图,下列说法错误的是( )
A.小明星期六参加体育运动的时间最少
B.小明星期四与星期六参加体育运动的时间之差为1 h
C.小明星期二参加体育运动的时长是60 min
D.小明星期四到星期日参加体育运动的时间越来越少
5.根据如图所示的程序计算函数y的值,若输入的x值为3或-3时,输出的y值相等,则a等于 ( )
A.-9 B.-3 C.9 D.3
6.(2024唐山滦南县期末)如果函数y=-2x+m的图像经过第二、三、四象限,那么m应满足的条件是 ( )
A.m>0 B.m<0 C.m≥0 D.m≤0
7.如图,矩形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=55°,则∠2的度数为 ( )
A.35° B.45° C.55° D.65°
8.如图,四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=6,CD=3,则MN的长可能是 ( )
A.4 B.6 C.8 D.10
9.盲道方便了盲人的通行,保持盲道畅通是我们每个人的义务.盲道一般由带有凸起的方形地砖铺设而成(图1).在部分盲道上建立平面直角坐标系,如图2,每个正方形的边长都为相同的整数个单位长度,则图中点P的坐标为 ( )
A.(10,1) B.(11,1)
C.(10,2) D.(11,3)
10.如图,已知菱形ABCD的对角线AC,BD相交于点O,E,P,F分别是线段OB,CD,OD的中点,连接EP,PF.若AC=8,PE=2,则菱形ABCD的面积为 ( )
A.64 B.48 C.24 D.16
11.如图1,在等腰三角形ABC中,∠ACB=90°,CD⊥AB于点D.动点P从点A出发,沿着A→D→C的路径以每秒1个单位长度的速度运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于点F.在此过程中四边形CEPF的面积y与运动时间x的函数关系图像如图2所示,则AB的长为 ( )
A.4 B.2 C.2 D.
12.动物园内的一段路线如图1所示,园内有免费的班车,从入口处出发,沿该线路开往熊猫馆,途中停靠海洋馆(上下车时间忽略不计),第一班车上午9:00发车,以后每隔10 min有一班车从入口处发车,且每班车速度均相同.小明周末到动物园游玩,上午8:35到达入口处,因还没到班车发车时间,于是从入口处出发沿该线路步行30 min后到达海洋馆.小明、第一班车与入口处的距离y(m)与时间x(min)的函数关系如图2所示,下列结论正确的是 ( )
A.第一班车从入口处到达熊猫馆所需的时间为15 min
B.第一班车与入口处的距离y(m)与时间x(min)的函数关系式为y=200x-4 000(25≤x≤45)
C.第一班车到达海洋馆时小明已经在海洋馆停留了10 min
D.小明在海洋馆游玩35 min后,想坐班车到熊猫馆,则小明最早能够坐上第四班车
二、填空题(本大题共4个小题,每小题3分,共12分)
13.点P(-2,3)关于坐标原点对称的点P'的坐标为 .
14.点A(x1,y1),B(x2,y2)都在直线y=(k-1)x+2(k<0)上,且x1
15.(2024石家庄藁城区期末)如图1,在某个盛有部分水的容器内放一个小水杯,现在匀速持续地向容器内注水,小水杯内水的高度y(cm)和注水时间t(s)之间的关系如图2所示,则从开始注水至把小水杯注满水需要的时间为 s.
16.如图,在正方形ABCD中,对角线AC,BD相交于点O,CE平分∠ACD交BD于点E,若DE=,则正方形ABCD的边长为 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)(2024沧州青县期末)在平面直角坐标系中,三角形ABC经过平移得到三角形A'B'C',位置如图所示.
(1)分别写出点A,A'的坐标.
(2)请说明三角形A'B'C'是由三角形ABC经过怎样的平移得到的.
(3)若M(m,4-n)是三角形ABC内部一点,则平移后对应点M'的坐标为(10-2n,m-1),求m和n的值.
18.(8分)(2024聊城阳谷县期末)高科技给我们的生活带来便利的同时,也给一些不法分子提供了可乘之机,他们的诈骗手段越来越难以防范.为了防止人们上当受骗,某公司开展了“经历最多的诈骗方式”的调查活动.经过整理分析后,绘制成了两个统计图.
(1)根据图中的信息可知,经历虚假中奖诈骗的有 人;经历电话欠费诈骗的人数占调查总人数的 %,有 人.
(2)把上面的两个统计图补充完整.
(3)为了防止诈骗,你想对身边的人说些什么
19.(8分)将长为40 cm,宽为15 cm的长方形白纸,按图所示的方法黏合起来,黏合部分宽为5 cm.
(1)根据图形,将表格补充完整.
白纸张数 1 2 3 4 5 …
纸条长度/cm 40 110 145 …
(2)设x张白纸黏合后的总长度为y cm,则y与x之间的关系式是什么
(3)你认为多少张白纸黏合起来总长度可能为2 035 cm 为什么
20.(8分)如图,四边形ABCD为平行四边形,∠BAD的平分线AF交CD于点E,交BC的延长线于点F.
(1)求证:BF=CD.
(2)连接BE,若BE⊥AF,∠BFA=60°,AB=4,求平行四边形ABCD的面积.
21.(8分)在平面直角坐标系中,给出如下定义:点P到x轴、y轴的距离的较大值称为点P的“长距”,点Q到x轴、y轴的距离相等时,称Q为“完美点”.
(1)点A(-1,3)的“长距”为 .
(2)若B(4a-1,-3)是“完美点”,求a的值.
(3)若点C(-2,3b-2)的长距为4,且点C在第二象限内,点D的坐标为(9-2b,-5),试说明:D是“完美点”.
22.(10分)十一期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以上信息,解答下列问题:
(1)设租车时间为x h,租用甲公司的车每日所需费用为y1元,租用乙公司的车每日所需费用为y2元,分别求出y1,y2关于x的函数表达式.
(2)当租车时间为多少小时时,两种方案所需费用相同
(3)根据(2)的计算结果,结合图像,请你帮助小明选择怎样的出游方案更合算.
23.(10分)(2024莆田荔城区期中)在菱形ABCD中,∠ABC=60°,P是直线BD上一动点,以AP为边向右侧作等边三角形APE(A,P,E按逆时针排列),点E的位置随点P的位置变化而变化.
(1)如图1,当点P在线段BD上,且点E在菱形ABCD内部或边上时,连接CE,则BP与CE的数量关系是 ,BC与CE的位置关系是 .
(2)如图2,当点P在线段BD上,且点E在菱形ABCD外部时,(1)中的结论是否还成立 若成立,请予以证明;若不成立,请说明理由.
24.(12分)某同学利用平面镜成像原理设计了一个游戏,如图,在y轴上放置一平面镜,从点A(2,5)处向平面镜发射一束光(看成线),经反射后沿直线l:y=mx+n(m≠0)传播.
(1)写出点A在平面镜内的虚像A'的坐标.
(2)若反射光束经过x轴上的点(8,0),求直线l的函数表达式.
(3)在x轴上从左到右有两点C,D,且CD=1,从点D向上作DB⊥x轴,且BD=2.
①若使△BCD沿x轴左右平移,且保证沿(2)中直线l传播的光束能照射到边BC(包括端点)上,则点B横坐标的最大值比最小值大多少
②若使△BCD位置固定,且点C的坐标为(9,0),仍保证沿直线l传播的光束能照射到边BC(包括端点)上,直接写出m的取值范围.
【详解答案】
1.A 解析:为了解某地区八年级学生的体质健康情况,从该地区13 000名八年级学生中随机抽取了1 000名学生进行体质健康情况调查,这次调查中的样本是被抽取的1 000名学生的体质健康情况.故选A.
2.B 解析:任意多边形的外角和都是360°,故正五边形的外角和为360°.故选B.
3.B 解析:由题意,得将点M向下平移3个单位长度,纵坐标为5-3=2,∴N(-3,2).故选B.
4.D 解析:由折线统计图可知,小明星期六参加体育运动时间最少,故A正确,不符合题意;小明星期四与星期六参加体育运动时间之差为70-10=60(min)=1(h),故B正确,不符合题意;小明星期二参加体育运动的时长是60 min,故C正确,不符合题意;小明星期四到星期六参加体育运动时间越来越少,故D错误,符合题意.故选D.
5.B 解析:当x=-3时,y=9+a;当x=3时,y=.根据题意,得9+a=,解得a=-3.故选B.
6.B 解析:∵函数y=-2x+m的图像经过第二、三、四象限,∴m<0.故选B.
7.C 解析:如图,延长AB交直线b于点E.∵a∥b,∴∠AEC=∠1=55°.∵四边形ABCD是矩形,∴AB∥CD.∴∠2=∠AEC=55°.故选C.
8.A 解析:如图,连接BD,取BD的中点E,连接ME,NE.∵M是AD的中点,E是BD的中点,∴ME=AB=3.同理,NE=CD=1.5.在△MNE中,3-1.5
∴OE=EB,OF=DF,PF∥AC,PF=OC=AC=2.∴PF⊥BD,∴EF==6.∴BD=2EF=12.
∴菱形ABCD的面积=AC·BD=×8×12=48.故选B.
11.A 解析:当点P运动到点D处时,如图,∴四边形CEPF的面积为y=2.∵PE⊥AC,PF⊥BC,∠ACB=90°,∴四边形CEPF为矩形.∵AC=BC,∴∠ACD=∠BCD,AD=BD.∴DE=DF.∴矩形DECF为正方形.∴DE2=2.∴DE=.∵∠A=45°,∴AD=DE=2.∴AB=4.故选A.
12.D 解析:A.第一班车从入口处到达熊猫馆所需的时间为45-25=20(min),故选项A错误,不符合题意;B.设第一班车与入口处的距离y(m)与时间x(min)的函数关系式为y=kx+b.将(25,0),(45,4 000)分别代入,得解得∴y=200x-5 000(25≤x≤45).故选项B错误,不符合题意;C.当y=2 400时,200x-5 000=2 400,∴x=37,而小明到达海洋馆的时间x=30,∴第一班车到达海洋馆时小明已经在海洋馆停留了7 min,故选项C错误,不符合题意;D.小明上午8:35到达入口处,到达海洋馆的时间是9:05,在海洋馆游玩35 min后是9:40,而第三班车9:20从入口处发车,经过37-25=12(min),即9:32到达海洋馆,小明不能赶上,第四班车9:30从入口处发车,9:42到达海洋馆,小明能赶上,故选项D正确,符合题意.故选D.
13.(2,-3) 解析:根据关于原点对称的点,横坐标与纵坐标都互为相反数求解.
14.> 解析:∵k<0,∴k-1<-1.∴y随x的增大而减小.又∵点A(x1,y1),B(x1,y2)都在直线y=(k-1)x+2(k<0)上,且x1
15.15 解析:设y与t的关系式为y=kt+b(k,b为常数,且k≠0).将坐标(10,0)和(12,4)代入y=kt+b,得解得∴y与t的关系式为y=2t-20(t≥10).当注满水杯时y=10,∴2t-20=10,解得t=15.
16.2+ 解析:如图,过点E作CD的垂线,垂足为M.∵四边形ABCD是正方形,∴∠ODC=45°,AC⊥BD,OD=OC.∴△DME是等腰直角三角形.又∵DE=,∴EM=1.∵CE平分∠ACD,EO⊥AC,EM⊥CD,∴EO=EM=1.∴OD= DE+OE=+1.∵△ODC是等腰直角三角形,∴DC=OD=2+.
17.解:(1)由题图可得A(1,0),A'(-4,4).
(2)三角形A'B'C'是由三角形ABC向左平移5个单位长度,向上平移4个单位长度得到的.
(3)由题意,得解得
18.解:(1)50 20 40
(2)1-10%-25%-20%=45%.
补全统计图如下:
(3)为了防止诈骗,我想对身边的人说:加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电.(答案不唯一).
19.解:(1)75 180
(2)根据题意和所给图形可得出:
y=40x-5(x-1)=35x+5,
∴y与x之间的关系式是y=35x+5.
(3)令y=2 035,得2 035=35x+5,
解得x=58.
∵x为整数,
∴58张白纸黏合,总长度为2 035 cm.
20.(1)证明:∵四边形ABCD为平行四边形,∴AB=CD,AD∥BC.
∴∠FAD=∠AFB.
又∵AF平分∠BAD,
∴∠FAD=∠FAB.
∴∠AFB=∠FAB.
∴AB=BF.∴BF=CD.
(2)解:∵∠F=60°,BF=AB=4,
∴△ABF是等边三角形.
∴∠ABF=60°.∴AF=AB=4.
∵BE⊥AF,
∴∠FBE=∠ABE=×60°=30°.
∴AE=EF=AF=2.
∴BE==2.
∴S△ABF=AF·BE=×4×2=4.
在△ADE和△FCE中,
∴△ADE≌△FCE(ASA).
∴S△ADE=S△FCE.
∴S△ADE+S四边形ABCE=S△FCE+S四边形ABCE,
即S平行四边形ABCD=S△ABF=4,
∴平行四边形ABCD的面积为4.
21.解:(1)3
(2)∵B(4a-1,-3)是“完美点”,
∴|4a-1|=|-3|.
∴4a-1=3或4a-1=-3,
解得a=1或a=-.
(3)∵点C(-2,3b-2)的长距为4,且点C在第二象限内,
∴3b-2=4,解得b=2.
∴9-2b=5.
∴点D的坐标为(5,-5).
∴D到x轴、y轴的距离都是5.
∴点D是“完美点”.
22.解:(1)设y1=k1x+80.
把点(1,95)代入,
可得95=k1+80,解得k1=15,
∴y1=15x+80(x≥0).
设y2=k2x.
把(1,30)代入,可得30=k2,即k2=30,∴y2=30x(x≥0).
(2)当y1=y2时,15x+80=30x,
解得x=.
∴当租车时间为 h时,两种方案所需费用相同.
(3)由(2)知,当y1=y2时,x=.
当y1>y2时,15x+80>30x,
解得x<;
当y1
∴当租车时间为 h,任意选择其中的一个方案;当租车时间小于 h,选择方案二合算;当租车时间大于 h,选择方案一合算.
23.解:(1)BP=CE BC⊥CE
解析:如图1,连接AC,延长CE交AD于点H.
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°.
∴AB=AC,∠BAC=60°,∠CAH=60°.
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°.
∵∠BAC=∠PAE,
∴∠BAP+∠PAC=∠CAE+∠PAC.
∴∠BAP=∠CAE.
∴△BAP≌△CAE(SAS).
∴BP=CE,∠ABP=∠ACE=30°.
∵△ACD是等边三角形,
∴∠ACD=2∠ACH=60°.
∴CH⊥AD,即CE⊥AD.
又∵AD∥BC,∴BC⊥CE.
(2)(1)中结论仍然成立.证明如下:如图2,连接AC.
则△ABC,△ACD为等边三角形.
在△ABP和△ACE中,AB=AC,AP=AE,
又∵∠BAP=∠BAC+∠CAP=60°+∠CAP,∠CAE=∠EAP+∠CAP=60°+∠CAP,
∴∠BAP=∠CAE.
∴△ABP≌△ACE(SAS).
∴BP=CE,∠ACE=∠ABD=30°.
设CE与AD交于点H.
同理可得∠ACD=2∠ACH=60°,
∴CE⊥AD.
又∵AD∥BC,∴CE⊥BC.
24.解:(1)∵A(2,5),∴A'(-2,5).
(2)把x=-2,y=5和x=8,y=0代入y=mx+n,
得解得
∴直线l的函数表达式为y=-x+4.
(3)①如图1.
由(2),得直线l的函数表达式为y=-x+4,
当y=2时,得2=-x+4,解得x=4,
当y=0时,由(2)可知x=8,
∴点B横坐标的最大值比最小值大(8+1)-4=5.
②m的取值范围为-≤m≤-.
解法提示:如图2.
由题意可得C(9,0),D(10,0),B(10,2),
将C(9,0),A'(-2,5)代入y=mx+n,
得解得m=-.
将B(10,2),A'(-2,5)代入y=mx+n,
得解得m=-.
故-≤m≤-.
同课章节目录
