专题训练八 构造三角形的中位线解题(含答案)2024-2025学年数学冀教版八年级下册
文档属性
| 名称 | 专题训练八 构造三角形的中位线解题(含答案)2024-2025学年数学冀教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 267.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:44:59 | ||
图片预览


文档简介
专题训练八 构造三角形的中位线解题
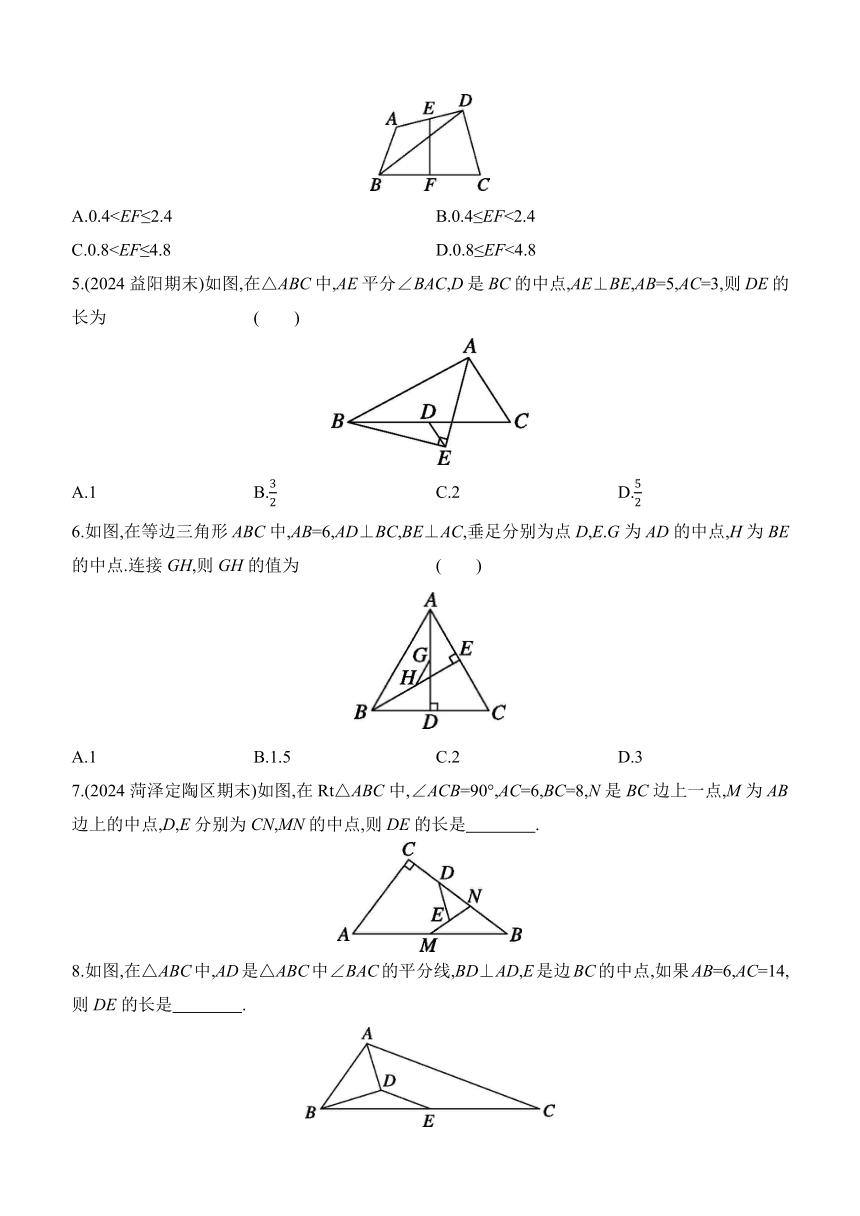
1.如图,某居民小区为了美化居住环境,要在一块三角形ABC空地上围一个四边形花坛BCFE.已知E,F分别是边AB,AC的中点,量得BC=16 m,则边EF的长是( )
A.6 m B.7 m C.8 m D.9 m
2.如图,已知四边形ABCD中,R,P分别是边DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,下列结论成立的是 ( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减小
C.线段EF的长不改变
D.线段EF的长的变化情况不能确定
3.如图,A,B为定点,定直线l∥AB,P是l上一动点,M,N分别为PA,PB的中点,对于下列各值:
①线段MN与AB的比值;
②△PAB的面积;
③△PMN的周长;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中随着点P的移动而变化的是 ( )
A.②③ B.②⑤
C.③⑤ D.①②④
4.如图,四边形ABCD中,BD为对角线,AB=2,CD=2.8,E,F分别是边AD,BC的中点,则EF的取值范围是 ( )
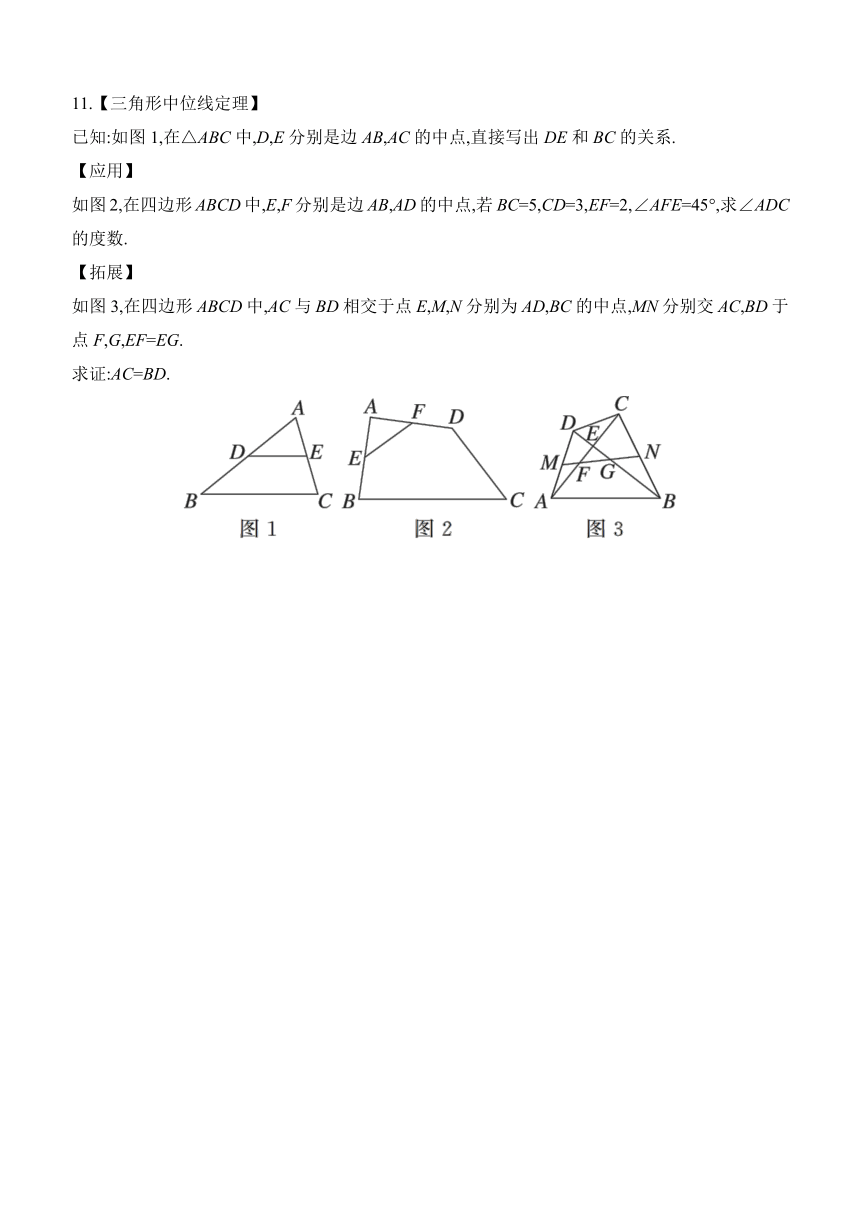
A.0.4C.0.85.(2024益阳期末)如图,在△ABC中,AE平分∠BAC,D是BC的中点,AE⊥BE,AB=5,AC=3,则DE的长为 ( )
A.1 B. C.2 D.
6.如图,在等边三角形ABC中,AB=6,AD⊥BC,BE⊥AC,垂足分别为点D,E.G为AD的中点,H为BE的中点.连接GH,则GH的值为 ( )
A.1 B.1.5 C.2 D.3
7.(2024菏泽定陶区期末)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,N是BC边上一点,M为AB边上的中点,D,E分别为CN,MN的中点,则DE的长是 .
8.如图,在△ABC中,AD是△ABC中∠BAC的平分线,BD⊥AD,E是边BC的中点,如果AB=6,AC=14,则DE的长是 .
9.如图,△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点.
求证:EF∥DG,且EF=DG.
10.在Rt△ABC中,∠ACB=90°,D是AB的中点,E是CA延长线上一点,且AE=AC.
(1)如图1,若BC=4,AC=2,求DE的长.
(2)如图2,F是DE的中点,求证:BD=2AF.
11.【三角形中位线定理】
已知:如图1,在△ABC中,D,E分别是边AB,AC的中点,直接写出DE和BC的关系.
【应用】
如图2,在四边形ABCD中,E,F分别是边AB,AD的中点,若BC=5,CD=3,EF=2,∠AFE=45°,求∠ADC的度数.
【拓展】
如图3,在四边形ABCD中,AC与BD相交于点E,M,N分别为AD,BC的中点,MN分别交AC,BD于点F,G,EF=EG.
求证:AC=BD.
【详解答案】
1.C 解析:∵E,F分别是边AB,AC的中点,BC=16 m,∴EF=BC=8 m.故选C.
2.C 解析:如图,连接AR.∵E,F分别是AP,RP的中点,∴EF为△APR的中位线.∴EF=AR,为定值.∴线段EF的长不改变.故选C.
3.C 解析:∵A,B为定点,∴AB长为定值.∵点M,N分别为PA,PB的中点,∴MN=AB,为定值,故①不正确.∵A,B为定点,定直线l∥AB,∴P到AB的距离为定值.∴△PAB的面积为定值.故②④不正确.当点P移动时,PA+PB的长发生变化,则PM+PN的长也发生变化,∴△PMN的周长发生变化,故③正确.当点P移动时,∠APB发生变化,故⑤正确.故选C.
4.A 解析:如图,取BD的中点H,连接EH,FH.∵E,H分别为AD,BD的中点,∴EH是△ABD的中位线.∴EH=AB =1.同理可得FH=CD=1.4.在△EHF中,FH-EH5.A 解析:如图,延长BE交AC的延长线于点F.∵AE⊥BE,∴∠AEB=∠AEF=90°.∵AE平分∠BAC,∴∠BAE=∠FAE.∴∠ABE=∠AFE.∴△ABF是等腰三角形.∴AF=AB=5,E是BF的中点.∴CF=AF-AC=5-3=2.又∵D是BC的中点,∴DE是△BCF的中位线.∴DE=CF=1.故选A.
6.B 解析:如图,取AB的中点F,连接GF,HF.∵△ABC为等边三角形,∴∠BAC=∠ABC=60°,AB=AC=BC.
∵AB=AC,AD⊥BC,BC=6,∴BD=BC=3.同理,AE=3.∵G,F分别为AD,AB的中点,∴GF是△ABD的中位线.
∴GF=BD=1.5,GF∥BD.∴∠AFG=∠ABC=60°.同理可得,FH=1.5,∠BFH=∠BAC=60°,∴GF=FH,∠GFH=60°,
∴△GFH为等边三角形.∴GH=GF=1.5.故选B.
7.2.5 解析:如图,连接CM.
∵∠ACB=90°,AC=6,BC=8,∴AB==10.∵M为AB边上的中点,∴CM=AB=5.∵D,E分别为CN,MN的中点,∴DE=CM=2.5,即DE的长是2.5.
8.4 解析:如图,延长BD交AC于点F.∵BD⊥AD,∴∠ADB=∠ADF.∵AD是△ABC中的∠BAC的平分线,
∴∠BAD=∠FAD.在△BAD和△FAD中,
∴△BAD≌△FAD(ASA).∴BD=FD,AF=AB=6.∴CF=AC-AF=8.∵E是边BC的中点,∴DE是△BCF的中位线.
∴DE=CF=4.故DE的长为4.
9.证明:如图,连接DE,FG.
∵BD,CE是△ABC的中线,
∴D,E分别是AC,AB边的中点.
∴DE∥BC,DE=BC.
同理,FG∥BC,FG=BC.
∴DE∥FG,DE=FG.
∴四边形DEFG是平行四边形.
∴EF∥DG,EF=DG.
10.(1)解:如图1,取AC的中点K,连接DK.
∴AK=AC=×2=1.
∵D是AB的中点,
∴DK是△ABC的中位线.
∴DK=BC=×4=2,DK∥BC.
∴∠EKD=∠C=90°.
∵EK=AE+AK=2+1=3,
∴DE=.
(2)证明:如图2,连接CD.
∵F是DE的中点,AE=AC,
∴AF是△EDC的中位线,
∴CD=2AF.
∵∠ACB=90°,D是AB的中点,
∴BD=CD.
∴BD=2AF.
11.解:【三角形中位线定理】DE∥BC,DE=BC.
【应用】连接BD,如图1所示.
∵E,F分别是边AB,AD的中点,
∴EF∥BD,BD=2EF=4.
∴∠ADB=∠AFE=45°.
∵BC=5,CD=3,
∴BD2+CD2=25,BC2=25.
∴BD2+CD2=BC2.∴∠BDC=90°.
∴∠ADC=∠ADB+∠BDC=135°.
【拓展】证明:如图2,取DC的中点H,连接MH,NH.
∵M,H分别是AD,DC的中点,
∴MH是△ADC的中位线.
∴MH∥AC且MH=AC.
同理可得NH∥BD且NH=BD.
∵EF=EG,∴∠EFG=∠EGF.
∵MH∥AC,NH∥BD,
∴∠EFG=∠HMN,∠EGF=∠HNM.
∴∠HMN=∠HNM.
∴MH=NH.∴AC=BD.
1.如图,某居民小区为了美化居住环境,要在一块三角形ABC空地上围一个四边形花坛BCFE.已知E,F分别是边AB,AC的中点,量得BC=16 m,则边EF的长是( )
A.6 m B.7 m C.8 m D.9 m
2.如图,已知四边形ABCD中,R,P分别是边DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,下列结论成立的是 ( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减小
C.线段EF的长不改变
D.线段EF的长的变化情况不能确定
3.如图,A,B为定点,定直线l∥AB,P是l上一动点,M,N分别为PA,PB的中点,对于下列各值:
①线段MN与AB的比值;
②△PAB的面积;
③△PMN的周长;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中随着点P的移动而变化的是 ( )
A.②③ B.②⑤
C.③⑤ D.①②④
4.如图,四边形ABCD中,BD为对角线,AB=2,CD=2.8,E,F分别是边AD,BC的中点,则EF的取值范围是 ( )
A.0.4
A.1 B. C.2 D.
6.如图,在等边三角形ABC中,AB=6,AD⊥BC,BE⊥AC,垂足分别为点D,E.G为AD的中点,H为BE的中点.连接GH,则GH的值为 ( )
A.1 B.1.5 C.2 D.3
7.(2024菏泽定陶区期末)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,N是BC边上一点,M为AB边上的中点,D,E分别为CN,MN的中点,则DE的长是 .
8.如图,在△ABC中,AD是△ABC中∠BAC的平分线,BD⊥AD,E是边BC的中点,如果AB=6,AC=14,则DE的长是 .
9.如图,△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点.
求证:EF∥DG,且EF=DG.
10.在Rt△ABC中,∠ACB=90°,D是AB的中点,E是CA延长线上一点,且AE=AC.
(1)如图1,若BC=4,AC=2,求DE的长.
(2)如图2,F是DE的中点,求证:BD=2AF.
11.【三角形中位线定理】
已知:如图1,在△ABC中,D,E分别是边AB,AC的中点,直接写出DE和BC的关系.
【应用】
如图2,在四边形ABCD中,E,F分别是边AB,AD的中点,若BC=5,CD=3,EF=2,∠AFE=45°,求∠ADC的度数.
【拓展】
如图3,在四边形ABCD中,AC与BD相交于点E,M,N分别为AD,BC的中点,MN分别交AC,BD于点F,G,EF=EG.
求证:AC=BD.
【详解答案】
1.C 解析:∵E,F分别是边AB,AC的中点,BC=16 m,∴EF=BC=8 m.故选C.
2.C 解析:如图,连接AR.∵E,F分别是AP,RP的中点,∴EF为△APR的中位线.∴EF=AR,为定值.∴线段EF的长不改变.故选C.
3.C 解析:∵A,B为定点,∴AB长为定值.∵点M,N分别为PA,PB的中点,∴MN=AB,为定值,故①不正确.∵A,B为定点,定直线l∥AB,∴P到AB的距离为定值.∴△PAB的面积为定值.故②④不正确.当点P移动时,PA+PB的长发生变化,则PM+PN的长也发生变化,∴△PMN的周长发生变化,故③正确.当点P移动时,∠APB发生变化,故⑤正确.故选C.
4.A 解析:如图,取BD的中点H,连接EH,FH.∵E,H分别为AD,BD的中点,∴EH是△ABD的中位线.∴EH=AB =1.同理可得FH=CD=1.4.在△EHF中,FH-EH
6.B 解析:如图,取AB的中点F,连接GF,HF.∵△ABC为等边三角形,∴∠BAC=∠ABC=60°,AB=AC=BC.
∵AB=AC,AD⊥BC,BC=6,∴BD=BC=3.同理,AE=3.∵G,F分别为AD,AB的中点,∴GF是△ABD的中位线.
∴GF=BD=1.5,GF∥BD.∴∠AFG=∠ABC=60°.同理可得,FH=1.5,∠BFH=∠BAC=60°,∴GF=FH,∠GFH=60°,
∴△GFH为等边三角形.∴GH=GF=1.5.故选B.
7.2.5 解析:如图,连接CM.
∵∠ACB=90°,AC=6,BC=8,∴AB==10.∵M为AB边上的中点,∴CM=AB=5.∵D,E分别为CN,MN的中点,∴DE=CM=2.5,即DE的长是2.5.
8.4 解析:如图,延长BD交AC于点F.∵BD⊥AD,∴∠ADB=∠ADF.∵AD是△ABC中的∠BAC的平分线,
∴∠BAD=∠FAD.在△BAD和△FAD中,
∴△BAD≌△FAD(ASA).∴BD=FD,AF=AB=6.∴CF=AC-AF=8.∵E是边BC的中点,∴DE是△BCF的中位线.
∴DE=CF=4.故DE的长为4.
9.证明:如图,连接DE,FG.
∵BD,CE是△ABC的中线,
∴D,E分别是AC,AB边的中点.
∴DE∥BC,DE=BC.
同理,FG∥BC,FG=BC.
∴DE∥FG,DE=FG.
∴四边形DEFG是平行四边形.
∴EF∥DG,EF=DG.
10.(1)解:如图1,取AC的中点K,连接DK.
∴AK=AC=×2=1.
∵D是AB的中点,
∴DK是△ABC的中位线.
∴DK=BC=×4=2,DK∥BC.
∴∠EKD=∠C=90°.
∵EK=AE+AK=2+1=3,
∴DE=.
(2)证明:如图2,连接CD.
∵F是DE的中点,AE=AC,
∴AF是△EDC的中位线,
∴CD=2AF.
∵∠ACB=90°,D是AB的中点,
∴BD=CD.
∴BD=2AF.
11.解:【三角形中位线定理】DE∥BC,DE=BC.
【应用】连接BD,如图1所示.
∵E,F分别是边AB,AD的中点,
∴EF∥BD,BD=2EF=4.
∴∠ADB=∠AFE=45°.
∵BC=5,CD=3,
∴BD2+CD2=25,BC2=25.
∴BD2+CD2=BC2.∴∠BDC=90°.
∴∠ADC=∠ADB+∠BDC=135°.
【拓展】证明:如图2,取DC的中点H,连接MH,NH.
∵M,H分别是AD,DC的中点,
∴MH是△ADC的中位线.
∴MH∥AC且MH=AC.
同理可得NH∥BD且NH=BD.
∵EF=EG,∴∠EFG=∠EGF.
∵MH∥AC,NH∥BD,
∴∠EFG=∠HMN,∠EGF=∠HNM.
∴∠HMN=∠HNM.
∴MH=NH.∴AC=BD.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
