专题训练二 坐标与线段长度和图形面积问题 (含答案)2024-2025学年数学冀教版八年级下册
文档属性
| 名称 | 专题训练二 坐标与线段长度和图形面积问题 (含答案)2024-2025学年数学冀教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 184.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:44:35 | ||
图片预览


文档简介
专题训练二 坐标与线段长度和图形面积问题
点的坐标与线段长度
1.(2024石家庄赵县期末)若点P的坐标为(-1,3),则点P到x轴的距离是 ( )
A.1 B.-1 C.3 D.-3
2.已知在平面直角坐标系xOy中,点A的坐标为(,2),则OA的长为 ( )
A. B. C.2 D.
3.已知AB∥x轴,A(-2,-4),AB=5,则B点的坐标为 ( )
A.(3,-4) B.(-2,1) C.(-7,-4) D.(3,-4)或(-7,-4)
4.阅读下列一段文字:已知在平面内两点P1(x1,y1),P2(x2,y2),其两点间的距离P1P2=.
问题解决:已知A(1,4),B(7,2).
(1)试求A,B两点的距离.
(2)在x轴上找一点P(不求坐标,画出图形即可),使PA+PB的长度最短,求PA+PB的最短长度.
5.在平面直角坐标系中,已知点P(2m+4,m-1).
(1)当点P在y轴上时,求点P的坐标.
(2)已知直线PA平行于y轴,且A(-4,-2),求AP的长.
(3)试判断点P是否可能在第二象限,并说明理由.
点的坐标与图形面积
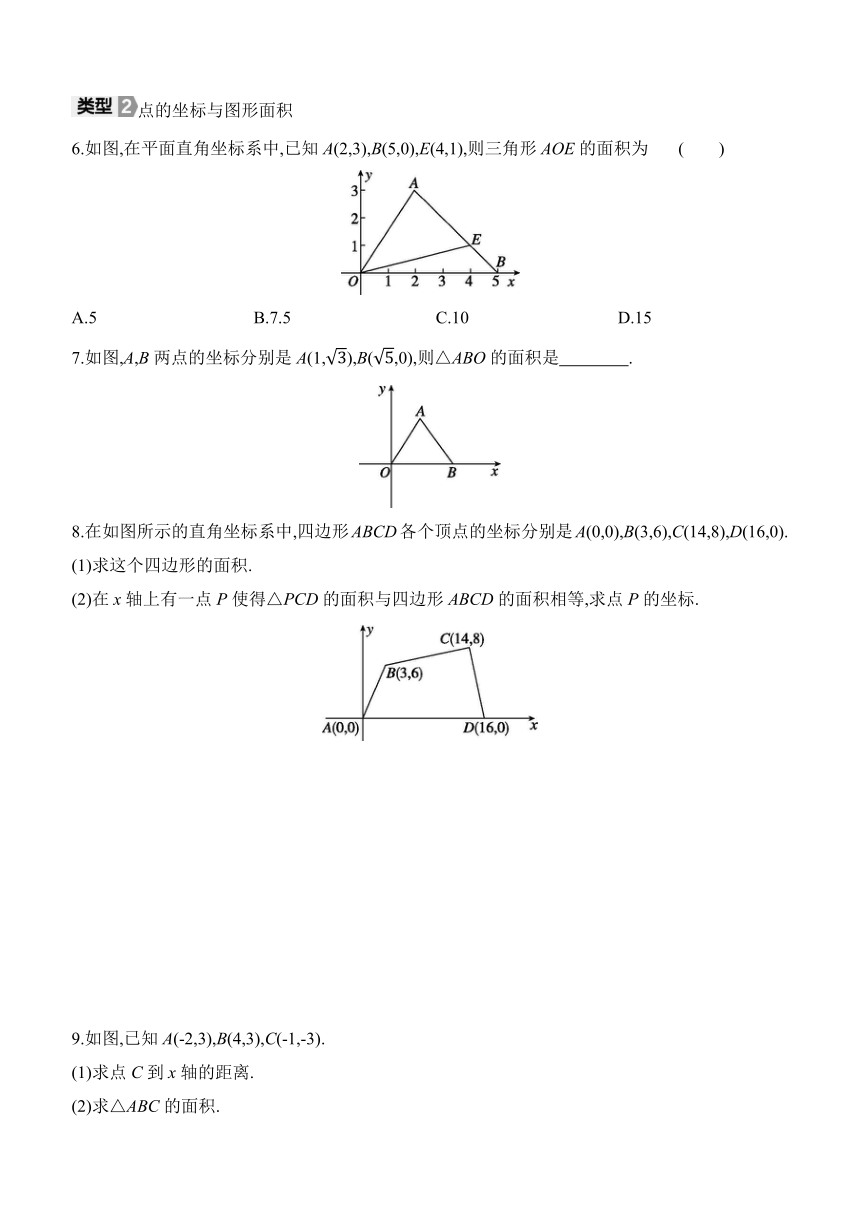
6.如图,在平面直角坐标系中,已知A(2,3),B(5,0),E(4,1),则三角形AOE的面积为 ( )
A.5 B.7.5 C.10 D.15
7.如图,A,B两点的坐标分别是A(1,),B(,0),则△ABO的面积是 .
8.在如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0).
(1)求这个四边形的面积.
(2)在x轴上有一点P使得△PCD的面积与四边形ABCD的面积相等,求点P的坐标.
9.如图,已知A(-2,3),B(4,3),C(-1,-3).
(1)求点C到x轴的距离.
(2)求△ABC的面积.
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
10.如图,在平面直角坐标系中,已知点A坐标为(-4,0),点B坐标为(-2,3),点Q坐标为(2,3),点Q关于x轴对称的点为C.
(1)在图中画出△ABC,并直接写出点C的坐标: .
(2)△ABC的面积为 .
(3)直接写出△ABC中边BC上的高为 .
11.如图,在平面直角坐标系中,点A(m,n).且m,n满足关系式m=-1,点B(-3,0),点C在x轴正半轴上,AC交y轴于点E.
(1)点A的坐标为 .
(2)若三角形ABC的面积为15,求线段BC的长.
(3)在(2)的条件下,动点P从点E出发,以每秒2个单位长度的速度先沿线段EO运动到点O,再继续以相同的速度沿x轴负半轴运动到点B后停止运动,△AOE的面积为.设点P运动的时间为
t s,直接写出当t为何值时,△AOE的面积是△BEP面积的一半.
【详解答案】
1.C 解析:∵点P的坐标为(-1,3),∴点P到x轴的距离是3.故选C.
2.A 解析:∵点A的坐标为(,2),∴OA=.故选A.
3.D 解析:∵AB∥x轴,∴A,B两点纵坐标相等,都是-4.又∵点A的坐标是(-2,-4),线段AB的长为5,∴当点B在点A左边时,点B的坐标为(-7,-4);当点B在点A右边时,点B的坐标为(3,-4).综上,点B的坐标为(-7,-4)或(3,-4).故选D.
4.解:(1)AB==2.
(2)如图,作点A关于x轴的对称点A'(1,-4),连接A'B,交x轴于点P,则PA+PB的最短长度是A'B的长,
∵A'B==6,
∴(PA+PB)最短=6.
5.解:(1)∵点P(2m+4,m-1)在y轴上,∴2m+4=0,解得m=-2.
∴m-1=-2-1=-3.
∴点P的坐标为(0,-3).
(2)∵直线PA平行于y轴,
∴2m+4=-4,解得m=-4.
∴m-1=-5.∴AP=-2-(-5)=3.
(3)不可能.理由:若点P在第二象限,
则不等式组无解,
∴点P不可能在第二象限.
6.A 解析:△AOE的面积=△OAB的面积-△OEB的面积=×5×3-×5×1=5.故选A.
7. 解析:根据题意可得,三角形OAB的面积=.
8.解:(1)如图,分别过B,C作x轴的垂线BE,CG,垂足分别为E,G.
所以S四边形ABCD=S△ABE+S梯形BEGC+S△CGD=×3×6+×11+×2×8=94.
(2)设P(x,0),∵△PCD的面积与四边形ABCD的面积相等,
∴|x-16|×8=94,
解得x1=,x2=-.
∴点P的坐标为或.
9.解:(1)∵C(-1,-3),
|-3|=3.
∴点C到x轴的距离为3.
(2)∵A(-2,3),B(4,3),C(-1,-3),
∴AB=4-(-2)=6,点C到边AB的距离为3-(-3)=6.
∴△ABC的面积为6×6÷2=18.
(3)点P的坐标为(0,1)或(0,5).
解法提示:设点P的坐标为(0,y).
∵△ABP的面积为6,
A(-2,3),B(4,3),
∴×6×|y-3|=6.
∴|y-3|=2.∴y=1或y=5.
∴点P的坐标为(0,1)或(0,5).
10.解:(1)如图所示:
(2,-3)
(2)12
(3)
解析:∵BC==2,S△ABC=12,∴BC·h=12.
∴h=.
故△ABC中边BC上的高为.
11.解:(1)(-1,5)
(2)如图,过点A作AF⊥x轴于点F.
∵A(-1,5),
∴AF=5.
∴S△ABC=×BC·AF=×BC×5=15.
∴BC=6.
(3)t的值为或.
解法提示:∵BC=6,B(-3,0),
∴C(3,0).
∵S△AOB+S△AOE+S△EOC=S△ABC=15,
∴×3×5+×1×OE+×3×OE=15.∴OE=.
①若点P在OE上,则PE=2t,
∴S△BEP=×2t×3=3t,
∵S△AOE=,
∴×3t=.∴t=.
②若点P在OB上,则BP=3+-2t=-2t,
∴S△BEP=.
∴.∴t=.
综上可得,t的值为或.
点的坐标与线段长度
1.(2024石家庄赵县期末)若点P的坐标为(-1,3),则点P到x轴的距离是 ( )
A.1 B.-1 C.3 D.-3
2.已知在平面直角坐标系xOy中,点A的坐标为(,2),则OA的长为 ( )
A. B. C.2 D.
3.已知AB∥x轴,A(-2,-4),AB=5,则B点的坐标为 ( )
A.(3,-4) B.(-2,1) C.(-7,-4) D.(3,-4)或(-7,-4)
4.阅读下列一段文字:已知在平面内两点P1(x1,y1),P2(x2,y2),其两点间的距离P1P2=.
问题解决:已知A(1,4),B(7,2).
(1)试求A,B两点的距离.
(2)在x轴上找一点P(不求坐标,画出图形即可),使PA+PB的长度最短,求PA+PB的最短长度.
5.在平面直角坐标系中,已知点P(2m+4,m-1).
(1)当点P在y轴上时,求点P的坐标.
(2)已知直线PA平行于y轴,且A(-4,-2),求AP的长.
(3)试判断点P是否可能在第二象限,并说明理由.
点的坐标与图形面积
6.如图,在平面直角坐标系中,已知A(2,3),B(5,0),E(4,1),则三角形AOE的面积为 ( )
A.5 B.7.5 C.10 D.15
7.如图,A,B两点的坐标分别是A(1,),B(,0),则△ABO的面积是 .
8.在如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0).
(1)求这个四边形的面积.
(2)在x轴上有一点P使得△PCD的面积与四边形ABCD的面积相等,求点P的坐标.
9.如图,已知A(-2,3),B(4,3),C(-1,-3).
(1)求点C到x轴的距离.
(2)求△ABC的面积.
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
10.如图,在平面直角坐标系中,已知点A坐标为(-4,0),点B坐标为(-2,3),点Q坐标为(2,3),点Q关于x轴对称的点为C.
(1)在图中画出△ABC,并直接写出点C的坐标: .
(2)△ABC的面积为 .
(3)直接写出△ABC中边BC上的高为 .
11.如图,在平面直角坐标系中,点A(m,n).且m,n满足关系式m=-1,点B(-3,0),点C在x轴正半轴上,AC交y轴于点E.
(1)点A的坐标为 .
(2)若三角形ABC的面积为15,求线段BC的长.
(3)在(2)的条件下,动点P从点E出发,以每秒2个单位长度的速度先沿线段EO运动到点O,再继续以相同的速度沿x轴负半轴运动到点B后停止运动,△AOE的面积为.设点P运动的时间为
t s,直接写出当t为何值时,△AOE的面积是△BEP面积的一半.
【详解答案】
1.C 解析:∵点P的坐标为(-1,3),∴点P到x轴的距离是3.故选C.
2.A 解析:∵点A的坐标为(,2),∴OA=.故选A.
3.D 解析:∵AB∥x轴,∴A,B两点纵坐标相等,都是-4.又∵点A的坐标是(-2,-4),线段AB的长为5,∴当点B在点A左边时,点B的坐标为(-7,-4);当点B在点A右边时,点B的坐标为(3,-4).综上,点B的坐标为(-7,-4)或(3,-4).故选D.
4.解:(1)AB==2.
(2)如图,作点A关于x轴的对称点A'(1,-4),连接A'B,交x轴于点P,则PA+PB的最短长度是A'B的长,
∵A'B==6,
∴(PA+PB)最短=6.
5.解:(1)∵点P(2m+4,m-1)在y轴上,∴2m+4=0,解得m=-2.
∴m-1=-2-1=-3.
∴点P的坐标为(0,-3).
(2)∵直线PA平行于y轴,
∴2m+4=-4,解得m=-4.
∴m-1=-5.∴AP=-2-(-5)=3.
(3)不可能.理由:若点P在第二象限,
则不等式组无解,
∴点P不可能在第二象限.
6.A 解析:△AOE的面积=△OAB的面积-△OEB的面积=×5×3-×5×1=5.故选A.
7. 解析:根据题意可得,三角形OAB的面积=.
8.解:(1)如图,分别过B,C作x轴的垂线BE,CG,垂足分别为E,G.
所以S四边形ABCD=S△ABE+S梯形BEGC+S△CGD=×3×6+×11+×2×8=94.
(2)设P(x,0),∵△PCD的面积与四边形ABCD的面积相等,
∴|x-16|×8=94,
解得x1=,x2=-.
∴点P的坐标为或.
9.解:(1)∵C(-1,-3),
|-3|=3.
∴点C到x轴的距离为3.
(2)∵A(-2,3),B(4,3),C(-1,-3),
∴AB=4-(-2)=6,点C到边AB的距离为3-(-3)=6.
∴△ABC的面积为6×6÷2=18.
(3)点P的坐标为(0,1)或(0,5).
解法提示:设点P的坐标为(0,y).
∵△ABP的面积为6,
A(-2,3),B(4,3),
∴×6×|y-3|=6.
∴|y-3|=2.∴y=1或y=5.
∴点P的坐标为(0,1)或(0,5).
10.解:(1)如图所示:
(2,-3)
(2)12
(3)
解析:∵BC==2,S△ABC=12,∴BC·h=12.
∴h=.
故△ABC中边BC上的高为.
11.解:(1)(-1,5)
(2)如图,过点A作AF⊥x轴于点F.
∵A(-1,5),
∴AF=5.
∴S△ABC=×BC·AF=×BC×5=15.
∴BC=6.
(3)t的值为或.
解法提示:∵BC=6,B(-3,0),
∴C(3,0).
∵S△AOB+S△AOE+S△EOC=S△ABC=15,
∴×3×5+×1×OE+×3×OE=15.∴OE=.
①若点P在OE上,则PE=2t,
∴S△BEP=×2t×3=3t,
∵S△AOE=,
∴×3t=.∴t=.
②若点P在OB上,则BP=3+-2t=-2t,
∴S△BEP=.
∴.∴t=.
综上可得,t的值为或.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
