专题训练三 平面直角坐标系中点的坐标变化规律(含答案)2024-2025学年数学冀教版八年级下册
文档属性
| 名称 | 专题训练三 平面直角坐标系中点的坐标变化规律(含答案)2024-2025学年数学冀教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 485.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:45:28 | ||
图片预览


文档简介
专题训练三 平面直角坐标系中点的坐标变化规律
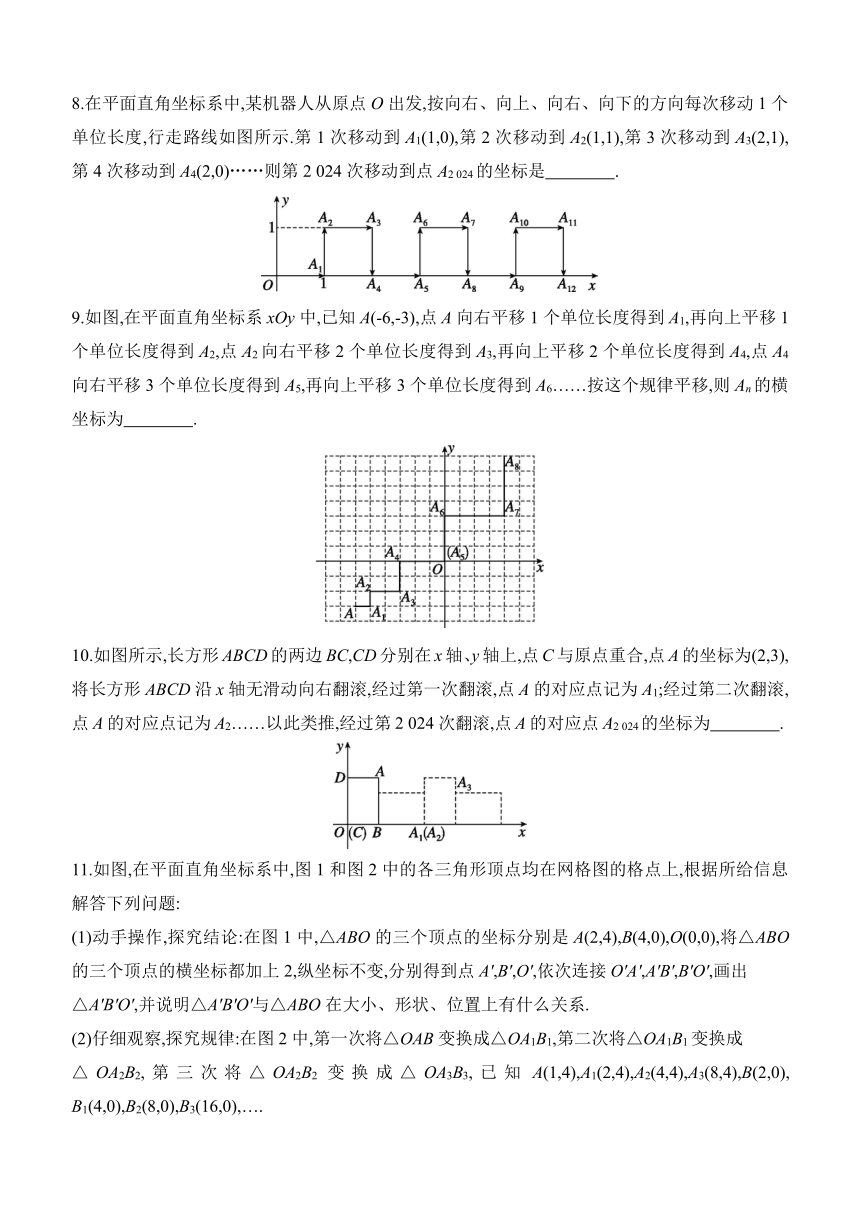
1.如图,在平面直角坐标系中,已知点B(0,6),点A在第一象限内,AB=OA,∠OAB=120°,将△ABO绕点O逆时针旋转,每次旋转90°,则第2 027次旋转结束时,点A的坐标为 ( )
A.(-3,) B.(-,3)
C.(,-3) D.(3,-)
2.如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2 030个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A—B—C—D—A…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是 ( )
A.(1,-1) B.(1,1)
C.(-1,-2) D.(1,-2)
3.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0),…,根据这个规律探索可得第2 024个点的坐标是 ( )
A.(63,5) B.(63,6)
C.(64,7) D.(64,6)
4.如图,在平面直角坐标系中,四边形OABC是正方形,顶点A(0,2)在y轴上,点C在x轴上,点B在第一象限,分别以点A,B为圆心,AB长为半径画弧,两弧交正方形内一点D,将点D绕点O逆时针旋转,每次旋转90°,则第2 024次旋转结束时,点D的对应点的坐标为 ( )
A.(1,2- ) B.(2-,-1)
C.(-1,-2) D.(-2+,1)
5.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(-2,3),则经过第2 024次变换后点A的对应点的坐标为 .
6.如图,在平面直角坐标系中,点P位于原点,第1 s向右移动1个单位长度,第2 s向上移动2个单位长度,第3 s向左移动3个单位长度,第4 s向下移动4个单位长度,第5 s向右移动5个单位长度……以此类推,经过2 024 s后,点P的坐标是 .
7.如图,在平面直角坐标系中有一个点P(1,0),点P第1次向上跳动 1个单位长度至点P1(1,1),紧接着第2次向左跳动2个单位长度至点P2(-1,1),第3次向上跳动1个单位长度,第4次向右跳动3个单位长度,第 5次又向上跳动1个单位长度,第6次向左跳动4个单位长度……按这个规律跳动下去,点P第2 024次跳动至点P2 024的坐标是 .
8.在平面直角坐标系中,某机器人从原点O出发,按向右、向上、向右、向下的方向每次移动1个单位长度,行走路线如图所示.第1次移动到A1(1,0),第2次移动到A2(1,1),第3次移动到A3(2,1),第4次移动到A4(2,0)……则第2 024次移动到点A2 024的坐标是 .
9.如图,在平面直角坐标系xOy中,已知A(-6,-3),点A向右平移1个单位长度得到A1,再向上平移1个单位长度得到A2,点A2向右平移2个单位长度得到A3,再向上平移2个单位长度得到A4,点A4向右平移3个单位长度得到A5,再向上平移3个单位长度得到A6……按这个规律平移,则An的横坐标为 .
10.如图所示,长方形ABCD的两边BC,CD分别在x轴、y轴上,点C与原点重合,点A的坐标为(2,3),将长方形ABCD沿x轴无滑动向右翻滚,经过第一次翻滚,点A的对应点记为A1;经过第二次翻滚,点A的对应点记为A2……以此类推,经过第2 024次翻滚,点A的对应点A2 024的坐标为 .
11.如图,在平面直角坐标系中,图1和图2中的各三角形顶点均在网格图的格点上,根据所给信息解答下列问题:
(1)动手操作,探究结论:在图1中,△ABO的三个顶点的坐标分别是A(2,4),B(4,0),O(0,0),将△ABO的三个顶点的横坐标都加上2,纵坐标不变,分别得到点A',B',O',依次连接O'A',A'B',B'O',画出
△A'B'O',并说明△A'B'O'与△ABO在大小、形状、位置上有什么关系.
(2)仔细观察,探究规律:在图2中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成
△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0), B1(4,0),B2(8,0),B3(16,0),….
①按此图形变化规律,写出△OA4B4的顶点坐标:A4 ,B4 ;
②通过计算得出△OA4B4的面积是△OAB面积的 倍;
③通过上述变化规律,请你猜想出△OAnBn的面积是△OAB面积的多少倍.
【详解答案】
1.D 解析:由题可知,将△ABO绕点O逆时针旋转,每次旋转90°,∴每旋转4次则回到原位置.∵2 027÷ 4=506……3,∴第2 027次旋转结束后,图形顺时针旋转了90°.如图所示,旋转后的图形为△OA1B1,作A1H⊥x轴于点H.∵AB=OA,∠OAB=120°,B(0,6),∴OH=OB=3.∴∠A1OH=∠AOB=30°.设A1H=x,则OA1=2x,在Rt△OA1H中,∵(2x)2=x2+32,∴x=(负值舍去).∵点A1在第四象限,∴A1(3,-).故选D.
2.B 解析:∵A(1,1),B(-1,1),C(-1,-2),D(1,-2),∴AB=1-(-1)=2,BC=1-(-2)=3,CD=1-(-1)=2,DA=1-(-2)=3.∴绕四边形ABCD一周的细线长度为2+3+2+3=10,∵2 030÷10=203,∴细线另一端在点A的位置,点的坐标为(1,1).故选B.
3.C 解析:横坐标为1的点有1个,横坐标为2的点有2个,横坐标为3的点有3个……所以横坐标为n的点有n个,则截止到横坐标为n(包含n)的点共有1+2+3+…+n=(个).当n=63时,=2 016,即截止到横坐标为63的点共有2 016个.又因为横坐标为偶数的点是从下往上排列的,且2 024-2 016=8,所以第2 024个点的坐标为(64,7).故选C.
4.A 解析:由题意知,△ABD是等边三角形.如图,过点D作AB的垂线,垂足为M.∵点A的坐标为(0,2),∴OA=2,则正方形ABCO的边长为2.∴AD=2,AM=1.在Rt△AMD中,DM=,∴点D的坐标为(1,2-).因为360°÷90°=4,所以每旋转四次点D的对应点循环出现.因为2 024÷4=506,所以第2 024次旋转结束时,点D的对应点的位置与点D重合.所以第2 024次旋转结束时,点D的对应点的坐标为(1,2-).故选A.
5.(-2,3) 解析:点A第一次关于y轴对称后在第一象限,点A第二次关于x轴对称后在第四象限,点A第三次关于y轴对称后在第三象限,点A第四次关于x轴对称后在第二象限,即点A回到原始位置,所以每四次对称为一个循环组,依次循环.∵2 024÷4=506,∴经过第2 024次变换后点A的对应点的坐标为(-2,3).
6.(-1 012,-1 012) 解析:观察题中图形可知,经过2 024 s后,点P在第三象限,且横、纵坐标相等.∵2 024÷4=506,∴P2 024的横坐标为-2×506=-1 012.∴经过2 024 s后点P的坐标为(-1 012,-1 012).
7.(507,1 012) 解析:第1次向上跳动1个单位长度至点P1(1,1),第2次向左跳动2个单位长度至点P2(-1,1),第3次向上跳动1个单位长度至点P3(-1,2),第4次向右跳动3个单位长度至点P4(2,2),第5次向上跳动1个单位长度至点P5(2,3),第6次向左跳动4个单位长度至点P6(-2,3),第7次向上跳动1个单位长度至点P7(-2,4),第8次向右跳动5个单位长度至点P8(3,4),第9次向上跳动1个单位长度至点P9(3,5),第10次向左跳动6个单位长度至点P10(-3,5),第11次向上跳动1个单位长度至点P11(-3,6),第12次向右跳动7个单位长度至点P12(4,6),第13次向上跳动1个单位长度至点P13(4,7),第14次向左跳动8个单位长度至点P14(-4,7)……跳动方向为4次一循环,2 024÷4=506,∴第2 024次为向右跳动得到,向右跳动至点Pn的坐标为,∴P2 024的坐标是(507,
1 012).
8.(1 012,0) 解析:由题意得,A1(1,0),A2(1,1),A3(2,1),A4(2,0),A5(3,0),A6(3,1),A7(4,1),A8(4,0),∴动点的纵坐标每4个完成一次循环,即OA4n=2n.∵2 024÷4=506,∴A2 024的坐标是(2×506,0),即(1 012,0).
9.-6 解析:∵点A向右平移1个单位长度得到A1,再向上平移1个单位长度得到A2;点A2向右平移2个单位长度得到A3,再向上平移2个单位长度得到A4;点A4向右平移3个单位长度得到A5,再向上平移3个单位长度得到A6……∴从点A开始,第偶数个点A2n的横坐标为-6+1+2+3+…+n=-6.∴An的横坐标为-6.
10.(5 062,3) 解析:根据所给翻滚方式可知,点A1的坐标为(5,0);点A2的坐标为(5,0);点A3的坐标为(7,2);点A4的坐标为(12,3);点A5的坐标为(15,0);点A6的坐标为(15,0);点A7的坐标为(17,2);点A8的坐标为(22,3)……由此可见,每翻滚四次,点Ai的横坐标增加10,且其纵坐标按0,0,2,3循环出现.又因为2 024÷4=506,12+10×(506-1)=5 062,所以点A2 024的坐标为(5 062,3).
11.解:(1)如图,△A'B'O'与△ABO的形状、大小完全相同,△A'B'O'可以看作将△ABO向右平移2个单位长度得到的.
(2)①(16,4) (32,0)
②16
解析:∵△OA4B4与△OAB的高都是4,OB4=32,OB=2,
∴×32×4=64,S△OAB=×2×4=4,∵64÷4=16,
∴△OA4B4的面积是△OAB面积的16倍.
③根据规律,后一个三角形的底边长是前一个三角形底边长的2倍,高相等都是4,∴OBn=2n+1.
∴×2n+1×4=2n+2.
∵S△OAB=×2×4=4,2n+2÷4=2n,
∴△OAnBn的面积是△OAB面积的2n倍.
1.如图,在平面直角坐标系中,已知点B(0,6),点A在第一象限内,AB=OA,∠OAB=120°,将△ABO绕点O逆时针旋转,每次旋转90°,则第2 027次旋转结束时,点A的坐标为 ( )
A.(-3,) B.(-,3)
C.(,-3) D.(3,-)
2.如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2 030个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A—B—C—D—A…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是 ( )
A.(1,-1) B.(1,1)
C.(-1,-2) D.(1,-2)
3.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0),…,根据这个规律探索可得第2 024个点的坐标是 ( )
A.(63,5) B.(63,6)
C.(64,7) D.(64,6)
4.如图,在平面直角坐标系中,四边形OABC是正方形,顶点A(0,2)在y轴上,点C在x轴上,点B在第一象限,分别以点A,B为圆心,AB长为半径画弧,两弧交正方形内一点D,将点D绕点O逆时针旋转,每次旋转90°,则第2 024次旋转结束时,点D的对应点的坐标为 ( )
A.(1,2- ) B.(2-,-1)
C.(-1,-2) D.(-2+,1)
5.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(-2,3),则经过第2 024次变换后点A的对应点的坐标为 .
6.如图,在平面直角坐标系中,点P位于原点,第1 s向右移动1个单位长度,第2 s向上移动2个单位长度,第3 s向左移动3个单位长度,第4 s向下移动4个单位长度,第5 s向右移动5个单位长度……以此类推,经过2 024 s后,点P的坐标是 .
7.如图,在平面直角坐标系中有一个点P(1,0),点P第1次向上跳动 1个单位长度至点P1(1,1),紧接着第2次向左跳动2个单位长度至点P2(-1,1),第3次向上跳动1个单位长度,第4次向右跳动3个单位长度,第 5次又向上跳动1个单位长度,第6次向左跳动4个单位长度……按这个规律跳动下去,点P第2 024次跳动至点P2 024的坐标是 .
8.在平面直角坐标系中,某机器人从原点O出发,按向右、向上、向右、向下的方向每次移动1个单位长度,行走路线如图所示.第1次移动到A1(1,0),第2次移动到A2(1,1),第3次移动到A3(2,1),第4次移动到A4(2,0)……则第2 024次移动到点A2 024的坐标是 .
9.如图,在平面直角坐标系xOy中,已知A(-6,-3),点A向右平移1个单位长度得到A1,再向上平移1个单位长度得到A2,点A2向右平移2个单位长度得到A3,再向上平移2个单位长度得到A4,点A4向右平移3个单位长度得到A5,再向上平移3个单位长度得到A6……按这个规律平移,则An的横坐标为 .
10.如图所示,长方形ABCD的两边BC,CD分别在x轴、y轴上,点C与原点重合,点A的坐标为(2,3),将长方形ABCD沿x轴无滑动向右翻滚,经过第一次翻滚,点A的对应点记为A1;经过第二次翻滚,点A的对应点记为A2……以此类推,经过第2 024次翻滚,点A的对应点A2 024的坐标为 .
11.如图,在平面直角坐标系中,图1和图2中的各三角形顶点均在网格图的格点上,根据所给信息解答下列问题:
(1)动手操作,探究结论:在图1中,△ABO的三个顶点的坐标分别是A(2,4),B(4,0),O(0,0),将△ABO的三个顶点的横坐标都加上2,纵坐标不变,分别得到点A',B',O',依次连接O'A',A'B',B'O',画出
△A'B'O',并说明△A'B'O'与△ABO在大小、形状、位置上有什么关系.
(2)仔细观察,探究规律:在图2中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成
△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0), B1(4,0),B2(8,0),B3(16,0),….
①按此图形变化规律,写出△OA4B4的顶点坐标:A4 ,B4 ;
②通过计算得出△OA4B4的面积是△OAB面积的 倍;
③通过上述变化规律,请你猜想出△OAnBn的面积是△OAB面积的多少倍.
【详解答案】
1.D 解析:由题可知,将△ABO绕点O逆时针旋转,每次旋转90°,∴每旋转4次则回到原位置.∵2 027÷ 4=506……3,∴第2 027次旋转结束后,图形顺时针旋转了90°.如图所示,旋转后的图形为△OA1B1,作A1H⊥x轴于点H.∵AB=OA,∠OAB=120°,B(0,6),∴OH=OB=3.∴∠A1OH=∠AOB=30°.设A1H=x,则OA1=2x,在Rt△OA1H中,∵(2x)2=x2+32,∴x=(负值舍去).∵点A1在第四象限,∴A1(3,-).故选D.
2.B 解析:∵A(1,1),B(-1,1),C(-1,-2),D(1,-2),∴AB=1-(-1)=2,BC=1-(-2)=3,CD=1-(-1)=2,DA=1-(-2)=3.∴绕四边形ABCD一周的细线长度为2+3+2+3=10,∵2 030÷10=203,∴细线另一端在点A的位置,点的坐标为(1,1).故选B.
3.C 解析:横坐标为1的点有1个,横坐标为2的点有2个,横坐标为3的点有3个……所以横坐标为n的点有n个,则截止到横坐标为n(包含n)的点共有1+2+3+…+n=(个).当n=63时,=2 016,即截止到横坐标为63的点共有2 016个.又因为横坐标为偶数的点是从下往上排列的,且2 024-2 016=8,所以第2 024个点的坐标为(64,7).故选C.
4.A 解析:由题意知,△ABD是等边三角形.如图,过点D作AB的垂线,垂足为M.∵点A的坐标为(0,2),∴OA=2,则正方形ABCO的边长为2.∴AD=2,AM=1.在Rt△AMD中,DM=,∴点D的坐标为(1,2-).因为360°÷90°=4,所以每旋转四次点D的对应点循环出现.因为2 024÷4=506,所以第2 024次旋转结束时,点D的对应点的位置与点D重合.所以第2 024次旋转结束时,点D的对应点的坐标为(1,2-).故选A.
5.(-2,3) 解析:点A第一次关于y轴对称后在第一象限,点A第二次关于x轴对称后在第四象限,点A第三次关于y轴对称后在第三象限,点A第四次关于x轴对称后在第二象限,即点A回到原始位置,所以每四次对称为一个循环组,依次循环.∵2 024÷4=506,∴经过第2 024次变换后点A的对应点的坐标为(-2,3).
6.(-1 012,-1 012) 解析:观察题中图形可知,经过2 024 s后,点P在第三象限,且横、纵坐标相等.∵2 024÷4=506,∴P2 024的横坐标为-2×506=-1 012.∴经过2 024 s后点P的坐标为(-1 012,-1 012).
7.(507,1 012) 解析:第1次向上跳动1个单位长度至点P1(1,1),第2次向左跳动2个单位长度至点P2(-1,1),第3次向上跳动1个单位长度至点P3(-1,2),第4次向右跳动3个单位长度至点P4(2,2),第5次向上跳动1个单位长度至点P5(2,3),第6次向左跳动4个单位长度至点P6(-2,3),第7次向上跳动1个单位长度至点P7(-2,4),第8次向右跳动5个单位长度至点P8(3,4),第9次向上跳动1个单位长度至点P9(3,5),第10次向左跳动6个单位长度至点P10(-3,5),第11次向上跳动1个单位长度至点P11(-3,6),第12次向右跳动7个单位长度至点P12(4,6),第13次向上跳动1个单位长度至点P13(4,7),第14次向左跳动8个单位长度至点P14(-4,7)……跳动方向为4次一循环,2 024÷4=506,∴第2 024次为向右跳动得到,向右跳动至点Pn的坐标为,∴P2 024的坐标是(507,
1 012).
8.(1 012,0) 解析:由题意得,A1(1,0),A2(1,1),A3(2,1),A4(2,0),A5(3,0),A6(3,1),A7(4,1),A8(4,0),∴动点的纵坐标每4个完成一次循环,即OA4n=2n.∵2 024÷4=506,∴A2 024的坐标是(2×506,0),即(1 012,0).
9.-6 解析:∵点A向右平移1个单位长度得到A1,再向上平移1个单位长度得到A2;点A2向右平移2个单位长度得到A3,再向上平移2个单位长度得到A4;点A4向右平移3个单位长度得到A5,再向上平移3个单位长度得到A6……∴从点A开始,第偶数个点A2n的横坐标为-6+1+2+3+…+n=-6.∴An的横坐标为-6.
10.(5 062,3) 解析:根据所给翻滚方式可知,点A1的坐标为(5,0);点A2的坐标为(5,0);点A3的坐标为(7,2);点A4的坐标为(12,3);点A5的坐标为(15,0);点A6的坐标为(15,0);点A7的坐标为(17,2);点A8的坐标为(22,3)……由此可见,每翻滚四次,点Ai的横坐标增加10,且其纵坐标按0,0,2,3循环出现.又因为2 024÷4=506,12+10×(506-1)=5 062,所以点A2 024的坐标为(5 062,3).
11.解:(1)如图,△A'B'O'与△ABO的形状、大小完全相同,△A'B'O'可以看作将△ABO向右平移2个单位长度得到的.
(2)①(16,4) (32,0)
②16
解析:∵△OA4B4与△OAB的高都是4,OB4=32,OB=2,
∴×32×4=64,S△OAB=×2×4=4,∵64÷4=16,
∴△OA4B4的面积是△OAB面积的16倍.
③根据规律,后一个三角形的底边长是前一个三角形底边长的2倍,高相等都是4,∴OBn=2n+1.
∴×2n+1×4=2n+2.
∵S△OAB=×2×4=4,2n+2÷4=2n,
∴△OAnBn的面积是△OAB面积的2n倍.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
