专题训练十 四边形的折叠与剪拼问题(含答案)2024-2025学年数学冀教版八年级下册
文档属性
| 名称 | 专题训练十 四边形的折叠与剪拼问题(含答案)2024-2025学年数学冀教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 264.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 00:00:00 | ||
图片预览

文档简介
专题训练十 四边形的折叠与剪拼问题
四边形的折叠问题
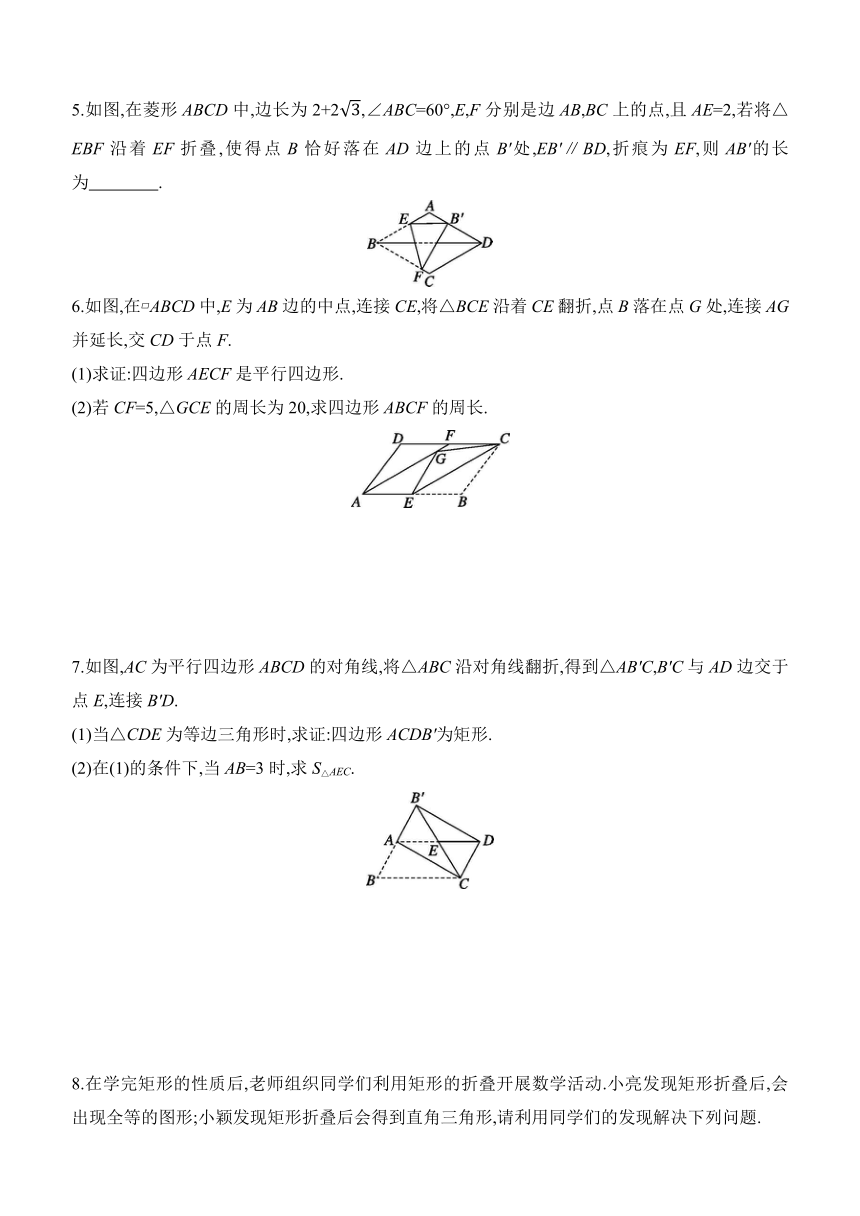
1.如图,在矩形ABCD中,AB=3 cm,AD=9 cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
A.6 cm2 B.8 cm2
C.10 cm2 D.12 cm2
2.如图,在菱形纸片ABCD中,∠A=60°,点E在BC边上,将菱形纸片ABCD沿DE折叠,点C的对应点为点C',且DC'是AB的垂直平分线,则∠DEC的度数为 ( )
A.30° B.45°
C.60° D.75°
3.如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上点B'处,则BE的长度为 ( )
A.1 B. C. D.2
4.如图,在正方形ABCD中,AB=6,点E在边CD上,且CE=2DE,将△ADE沿AE折叠得到△AFE,延长EF交边BC于点G,则BG的长为 ( )
A.2 B. C.3 D.
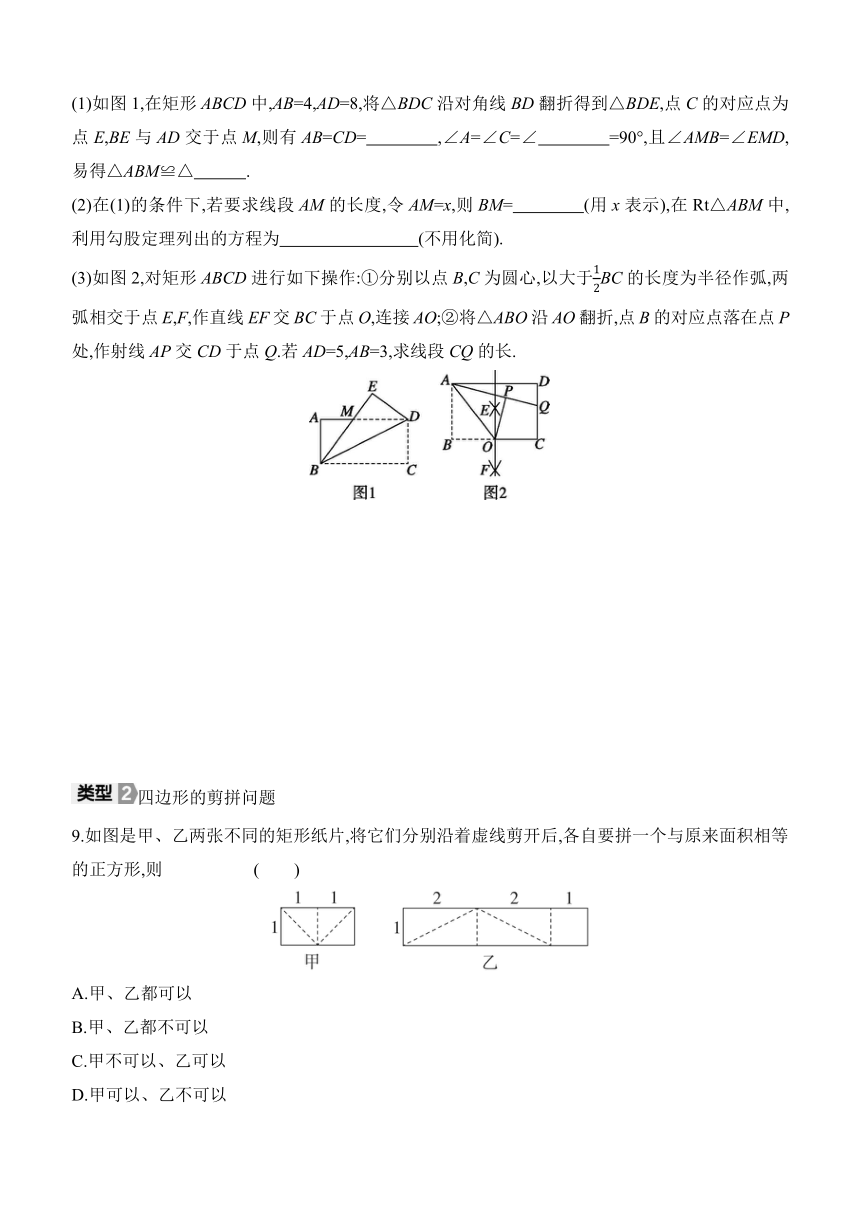
5.如图,在菱形ABCD中,边长为2+2,∠ABC=60°,E,F分别是边AB,BC上的点,且AE=2,若将△EBF沿着EF折叠,使得点B恰好落在AD边上的点B'处,EB'∥BD,折痕为EF,则AB'的长为 .
6.如图,在 ABCD中,E为AB边的中点,连接CE,将△BCE沿着CE翻折,点B落在点G处,连接AG并延长,交CD于点F.
(1)求证:四边形AECF是平行四边形.
(2)若CF=5,△GCE的周长为20,求四边形ABCF的周长.
7.如图,AC为平行四边形ABCD的对角线,将△ABC沿对角线翻折,得到△AB'C,B'C与AD边交于点E,连接B'D.
(1)当△CDE为等边三角形时,求证:四边形ACDB'为矩形.
(2)在(1)的条件下,当AB=3时,求S△AEC.
8.在学完矩形的性质后,老师组织同学们利用矩形的折叠开展数学活动.小亮发现矩形折叠后,会出现全等的图形;小颖发现矩形折叠后会得到直角三角形,请利用同学们的发现解决下列问题.
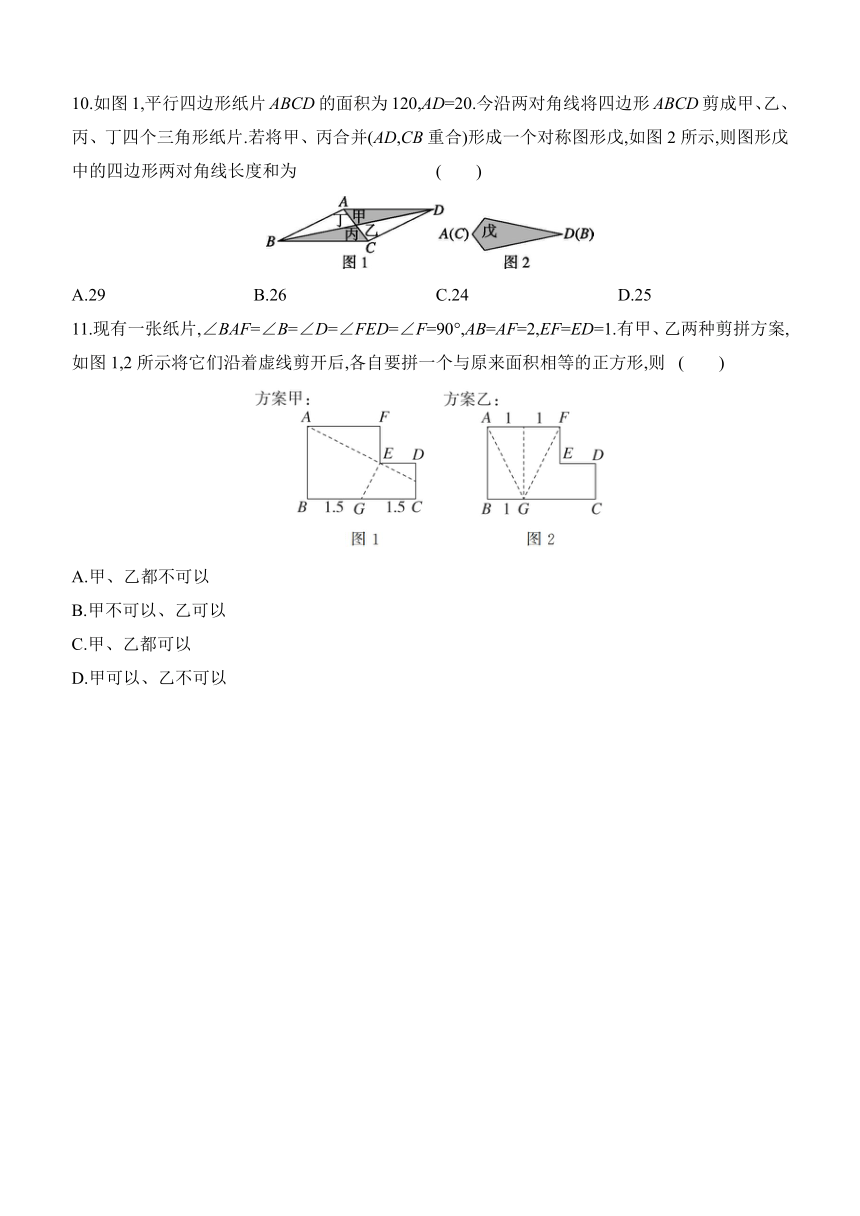
(1)如图1,在矩形ABCD中,AB=4,AD=8,将△BDC沿对角线BD翻折得到△BDE,点C的对应点为点E,BE与AD交于点M,则有AB=CD= ,∠A=∠C=∠ =90°,且∠AMB=∠EMD,易得△ABM≌△ .
(2)在(1)的条件下,若要求线段AM的长度,令AM=x,则BM= (用x表示),在Rt△ABM中,利用勾股定理列出的方程为 (不用化简).
(3)如图2,对矩形ABCD进行如下操作:①分别以点B,C为圆心,以大于BC的长度为半径作弧,两弧相交于点E,F,作直线EF交BC于点O,连接AO;②将△ABO沿AO翻折,点B的对应点落在点P处,作射线AP交CD于点Q.若AD=5,AB=3,求线段CQ的长.
四边形的剪拼问题
9.如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则 ( )
A.甲、乙都可以
B.甲、乙都不可以
C.甲不可以、乙可以
D.甲可以、乙不可以
10.如图1,平行四边形纸片ABCD的面积为120,AD=20.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD,CB重合)形成一个对称图形戊,如图2所示,则图形戊中的四边形两对角线长度和为 ( )
A.29 B.26 C.24 D.25
11.现有一张纸片,∠BAF=∠B=∠D=∠FED=∠F=90°,AB=AF=2,EF=ED=1.有甲、乙两种剪拼方案,如图1,2所示将它们沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则 ( )
A.甲、乙都不可以
B.甲不可以、乙可以
C.甲、乙都可以
D.甲可以、乙不可以
【详解答案】
1.A 解析:将此长方形折叠,使点B与点D重合,∴BE=ED.∵AD=AE+DE=AE+BE=9 cm,∴BE=9-AE.根据勾股定理可知,AB2+AE2=BE2.解得AE=4.∴△ABE的面积为×3×4=6(cm2).故选A.
2.D 解析:如图,连接BD.∵四边形ABCD为菱形,∴AB=AD.∵∠A=60°,∴△ABD为等边三角形,∠ADC=120°,∠C=60°.∵DC'是AB的垂直平分线,∴P为AB的中点.∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°.
∴∠PDC=90°.∴由折叠的性质得到∠CDE=∠PDE=45°.在△DEC中,∠DEC=180°-(∠CDE+∠C)=75°.故选D.
3.D 解析:∵四边形ABCD是正方形,∴AB∥CD,∠A=90°.∴∠BEF=∠EFD=60°.∵将四边形EBCF沿EF折叠,点B恰好落在AD边上点B'处,∴∠BEF=∠FEB'=60°,BE=B'E.∴∠AEB'=180°-∠BEF-∠FEB'=60°,∴B'E=2AE.设BE=x,则B'E=x,AE=3-x.∴2(3-x)=x,解得x=2.故选D.
4.C 解析:∵四边形ABCD是正方形,∴AB=AD=6,∠B=∠D=90°.由折叠,得AD=AF,∠D=∠AFE=90°,∴∠B=
∠AFG=90°,AF=AB.∵在Rt△ABG和Rt△AFG中,∴Rt△ABG≌Rt△AFG(HL).∴BG=GF.∵CE=2DE,∴DE=2,CE=4.设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2.在Rt△ECG中,由勾股定理,得CG2+CE2=EG2.∴(6-x)2+42=(x+2)2.解得x=3,∴BG=3.故选C.
5.2 解析:∵四边形ABCD是菱形,∠ABC=60°,对角线平分对角,∴∠BAD=120°,∠DBE=30°.又∵EB'∥BD,
∴∠DBE=∠AEB'=30°.又∵∠BAD=120°,∴∠AB'E=30°.∴AB'=AE=2.
6.(1)证明:∵四边形ABCD是平行四边形,∴AE∥FC.
∵E是AB边的中点,
∴AE=BE.
∵将△BCE沿着CE翻折,点B落在点G处,
∴BE=GE,∠CEB=∠CEG.
∴AE=GE.
∴∠FAE=∠AGE.
∵∠CEB=∠CEG=∠BEG,∠BEG=∠FAE+∠AGE,
∴∠FAE=∠BEG.
∴∠FAE=∠CEB.∴AF∥EC.
∴四边形AECF是平行四边形.
(2)解:由折叠的性质,得GE=BE,GC=BC.
∵△GCE的周长为20,
∴GE+CE+GC=20.
∴BE+CE+BC=20.
∵四边形AECF是平行四边形,
∴AF=CE,AE=CF=5.
∴四边形ABCF的周长=AB+BC+CF+AF=AE+BE+BC+CE+CF=5+20+5=30.
7.(1)证明:∵△CDE是等边三角形,
∴DE=DC=EC,
∠ADC=∠CED=60°.
根据折叠的性质可知,
∠BCA=∠B'CA.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠EAC=∠BCA.
∴∠EAC=∠ECA.
∴EA=EC.
∴∠DAC=∠ECA=30°.
∴∠ACD=90°.
∵AB∥CD,
∴∠BAC=∠ACD=90°.
∴AC⊥AB.
由折叠可知,∠B'AC=∠BAC=90°,
∴B,A,B'三点在同一条直线上.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
由折叠可知,AB=AB',
∴AB'∥CD,AB'=CD.
∴四边形ACDB'为平行四边形.
∵∠ACD=90°,
∴四边形ACDB'为矩形.
(2)解:在Rt△ACB'中,∠CAB'=90°.
∵∠ACB'=30°,AB'=AB=3,
∴CB'=6,∴AC=3.
∴S△AEC=S△ACB'=×AC·AB'=×3×3=.
8.解:(1)ED E EDM
(2)8-x 42+x2=(8-x)2
(3)如图,连接OQ.
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=5.
由作图知BO=OC=BC=2.5,
由翻折的性质,得AP=AB=3,OP=OB=2.5,∠APO=∠B=90°,
∴OP=OC=2.5,∠QPO=∠C=90°.
又∵OQ=OQ,
∴Rt△QPO≌Rt△QCO(HL).
∴PQ=CQ.
设PQ=CQ=m,则AQ=3+m,DQ=3-m.
在Rt△ADQ中,AD2+QD2=AQ2,
即52+(3-m)2=(3+m)2,
解得m=,
∴线段CQ的长为.
9.A 解析:所作图形如图所示,甲、乙都可以拼一个与原来面积相等的正方形.故选A.
10.B 解析:如图,连接AD,EF.
则EF⊥AD,且EF与平行四边形ABCD的高相等.∵平行四边形纸片ABCD的面积为120,AD=20,∴BC =AD=20,EF·AD=120,∴EF=6,∴图形戊中的四边形两对角线长度和为20+6=26.故选B.
11.C 解析:如图1,将△AEF移至①处,△DEH移至②处,四边形GCHE移至③处,即可得到一个与原来面积相等的正方形;如图2,将△ABG,△AHG,△HGF分别移至①②③处,即可得到一个与原来面积相等的正方形.∴甲、乙方案都可以.故选C.
四边形的折叠问题
1.如图,在矩形ABCD中,AB=3 cm,AD=9 cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
A.6 cm2 B.8 cm2
C.10 cm2 D.12 cm2
2.如图,在菱形纸片ABCD中,∠A=60°,点E在BC边上,将菱形纸片ABCD沿DE折叠,点C的对应点为点C',且DC'是AB的垂直平分线,则∠DEC的度数为 ( )
A.30° B.45°
C.60° D.75°
3.如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上点B'处,则BE的长度为 ( )
A.1 B. C. D.2
4.如图,在正方形ABCD中,AB=6,点E在边CD上,且CE=2DE,将△ADE沿AE折叠得到△AFE,延长EF交边BC于点G,则BG的长为 ( )
A.2 B. C.3 D.
5.如图,在菱形ABCD中,边长为2+2,∠ABC=60°,E,F分别是边AB,BC上的点,且AE=2,若将△EBF沿着EF折叠,使得点B恰好落在AD边上的点B'处,EB'∥BD,折痕为EF,则AB'的长为 .
6.如图,在 ABCD中,E为AB边的中点,连接CE,将△BCE沿着CE翻折,点B落在点G处,连接AG并延长,交CD于点F.
(1)求证:四边形AECF是平行四边形.
(2)若CF=5,△GCE的周长为20,求四边形ABCF的周长.
7.如图,AC为平行四边形ABCD的对角线,将△ABC沿对角线翻折,得到△AB'C,B'C与AD边交于点E,连接B'D.
(1)当△CDE为等边三角形时,求证:四边形ACDB'为矩形.
(2)在(1)的条件下,当AB=3时,求S△AEC.
8.在学完矩形的性质后,老师组织同学们利用矩形的折叠开展数学活动.小亮发现矩形折叠后,会出现全等的图形;小颖发现矩形折叠后会得到直角三角形,请利用同学们的发现解决下列问题.
(1)如图1,在矩形ABCD中,AB=4,AD=8,将△BDC沿对角线BD翻折得到△BDE,点C的对应点为点E,BE与AD交于点M,则有AB=CD= ,∠A=∠C=∠ =90°,且∠AMB=∠EMD,易得△ABM≌△ .
(2)在(1)的条件下,若要求线段AM的长度,令AM=x,则BM= (用x表示),在Rt△ABM中,利用勾股定理列出的方程为 (不用化简).
(3)如图2,对矩形ABCD进行如下操作:①分别以点B,C为圆心,以大于BC的长度为半径作弧,两弧相交于点E,F,作直线EF交BC于点O,连接AO;②将△ABO沿AO翻折,点B的对应点落在点P处,作射线AP交CD于点Q.若AD=5,AB=3,求线段CQ的长.
四边形的剪拼问题
9.如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则 ( )
A.甲、乙都可以
B.甲、乙都不可以
C.甲不可以、乙可以
D.甲可以、乙不可以
10.如图1,平行四边形纸片ABCD的面积为120,AD=20.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD,CB重合)形成一个对称图形戊,如图2所示,则图形戊中的四边形两对角线长度和为 ( )
A.29 B.26 C.24 D.25
11.现有一张纸片,∠BAF=∠B=∠D=∠FED=∠F=90°,AB=AF=2,EF=ED=1.有甲、乙两种剪拼方案,如图1,2所示将它们沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则 ( )
A.甲、乙都不可以
B.甲不可以、乙可以
C.甲、乙都可以
D.甲可以、乙不可以
【详解答案】
1.A 解析:将此长方形折叠,使点B与点D重合,∴BE=ED.∵AD=AE+DE=AE+BE=9 cm,∴BE=9-AE.根据勾股定理可知,AB2+AE2=BE2.解得AE=4.∴△ABE的面积为×3×4=6(cm2).故选A.
2.D 解析:如图,连接BD.∵四边形ABCD为菱形,∴AB=AD.∵∠A=60°,∴△ABD为等边三角形,∠ADC=120°,∠C=60°.∵DC'是AB的垂直平分线,∴P为AB的中点.∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°.
∴∠PDC=90°.∴由折叠的性质得到∠CDE=∠PDE=45°.在△DEC中,∠DEC=180°-(∠CDE+∠C)=75°.故选D.
3.D 解析:∵四边形ABCD是正方形,∴AB∥CD,∠A=90°.∴∠BEF=∠EFD=60°.∵将四边形EBCF沿EF折叠,点B恰好落在AD边上点B'处,∴∠BEF=∠FEB'=60°,BE=B'E.∴∠AEB'=180°-∠BEF-∠FEB'=60°,∴B'E=2AE.设BE=x,则B'E=x,AE=3-x.∴2(3-x)=x,解得x=2.故选D.
4.C 解析:∵四边形ABCD是正方形,∴AB=AD=6,∠B=∠D=90°.由折叠,得AD=AF,∠D=∠AFE=90°,∴∠B=
∠AFG=90°,AF=AB.∵在Rt△ABG和Rt△AFG中,∴Rt△ABG≌Rt△AFG(HL).∴BG=GF.∵CE=2DE,∴DE=2,CE=4.设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2.在Rt△ECG中,由勾股定理,得CG2+CE2=EG2.∴(6-x)2+42=(x+2)2.解得x=3,∴BG=3.故选C.
5.2 解析:∵四边形ABCD是菱形,∠ABC=60°,对角线平分对角,∴∠BAD=120°,∠DBE=30°.又∵EB'∥BD,
∴∠DBE=∠AEB'=30°.又∵∠BAD=120°,∴∠AB'E=30°.∴AB'=AE=2.
6.(1)证明:∵四边形ABCD是平行四边形,∴AE∥FC.
∵E是AB边的中点,
∴AE=BE.
∵将△BCE沿着CE翻折,点B落在点G处,
∴BE=GE,∠CEB=∠CEG.
∴AE=GE.
∴∠FAE=∠AGE.
∵∠CEB=∠CEG=∠BEG,∠BEG=∠FAE+∠AGE,
∴∠FAE=∠BEG.
∴∠FAE=∠CEB.∴AF∥EC.
∴四边形AECF是平行四边形.
(2)解:由折叠的性质,得GE=BE,GC=BC.
∵△GCE的周长为20,
∴GE+CE+GC=20.
∴BE+CE+BC=20.
∵四边形AECF是平行四边形,
∴AF=CE,AE=CF=5.
∴四边形ABCF的周长=AB+BC+CF+AF=AE+BE+BC+CE+CF=5+20+5=30.
7.(1)证明:∵△CDE是等边三角形,
∴DE=DC=EC,
∠ADC=∠CED=60°.
根据折叠的性质可知,
∠BCA=∠B'CA.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠EAC=∠BCA.
∴∠EAC=∠ECA.
∴EA=EC.
∴∠DAC=∠ECA=30°.
∴∠ACD=90°.
∵AB∥CD,
∴∠BAC=∠ACD=90°.
∴AC⊥AB.
由折叠可知,∠B'AC=∠BAC=90°,
∴B,A,B'三点在同一条直线上.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
由折叠可知,AB=AB',
∴AB'∥CD,AB'=CD.
∴四边形ACDB'为平行四边形.
∵∠ACD=90°,
∴四边形ACDB'为矩形.
(2)解:在Rt△ACB'中,∠CAB'=90°.
∵∠ACB'=30°,AB'=AB=3,
∴CB'=6,∴AC=3.
∴S△AEC=S△ACB'=×AC·AB'=×3×3=.
8.解:(1)ED E EDM
(2)8-x 42+x2=(8-x)2
(3)如图,连接OQ.
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=5.
由作图知BO=OC=BC=2.5,
由翻折的性质,得AP=AB=3,OP=OB=2.5,∠APO=∠B=90°,
∴OP=OC=2.5,∠QPO=∠C=90°.
又∵OQ=OQ,
∴Rt△QPO≌Rt△QCO(HL).
∴PQ=CQ.
设PQ=CQ=m,则AQ=3+m,DQ=3-m.
在Rt△ADQ中,AD2+QD2=AQ2,
即52+(3-m)2=(3+m)2,
解得m=,
∴线段CQ的长为.
9.A 解析:所作图形如图所示,甲、乙都可以拼一个与原来面积相等的正方形.故选A.
10.B 解析:如图,连接AD,EF.
则EF⊥AD,且EF与平行四边形ABCD的高相等.∵平行四边形纸片ABCD的面积为120,AD=20,∴BC =AD=20,EF·AD=120,∴EF=6,∴图形戊中的四边形两对角线长度和为20+6=26.故选B.
11.C 解析:如图1,将△AEF移至①处,△DEH移至②处,四边形GCHE移至③处,即可得到一个与原来面积相等的正方形;如图2,将△ABG,△AHG,△HGF分别移至①②③处,即可得到一个与原来面积相等的正方形.∴甲、乙方案都可以.故选C.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
