17.3 一次函数 2.一次函数的图象 同步练(含答案)2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 17.3 一次函数 2.一次函数的图象 同步练(含答案)2024-2025学年数学华东师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 228.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:50:51 | ||
图片预览


文档简介
2.一次函数的图象
一次函数的图象
1.下列各点在函数y=2x-1图象上的是 ( )
A.(-1,3) B.(0,1) C.(1,-1) D.(2,3)
2.一次函数y=-3x+1的图象经过 ( )
A.第一、二、四象限
B.第一、三、四象限
C.第一、二、三象限
D.第二、三、四象限
3.如果一次函数y=kx+4的图象经过点P(-1,3),则k= ;当x=2时,y= ;当y=4时, x= .
4.若一次函数y=-2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是 .(写出一个即可)
5.已知一次函数y=-2x-2.
(1)若该函数的图象与x轴、y轴分别交于A、B两点,求点A、B的坐标.
(2)在给定的平面直角坐标系(如图)中画出函数的图象.
一次函数图象的平移
6.将直线y=5x向下平移2个单位,所得直线的关系式为 ( )
A.y=5x-2 B.y=5x+2 C.y=5(x+2) D.y=5(x-2)
7.已知一次函数 y=kx+1的图象与y=x的图象平行,那么它必过点 ( )
A.(-1,0) B.(2,-1)
C.(2,1) D.(0,-1)
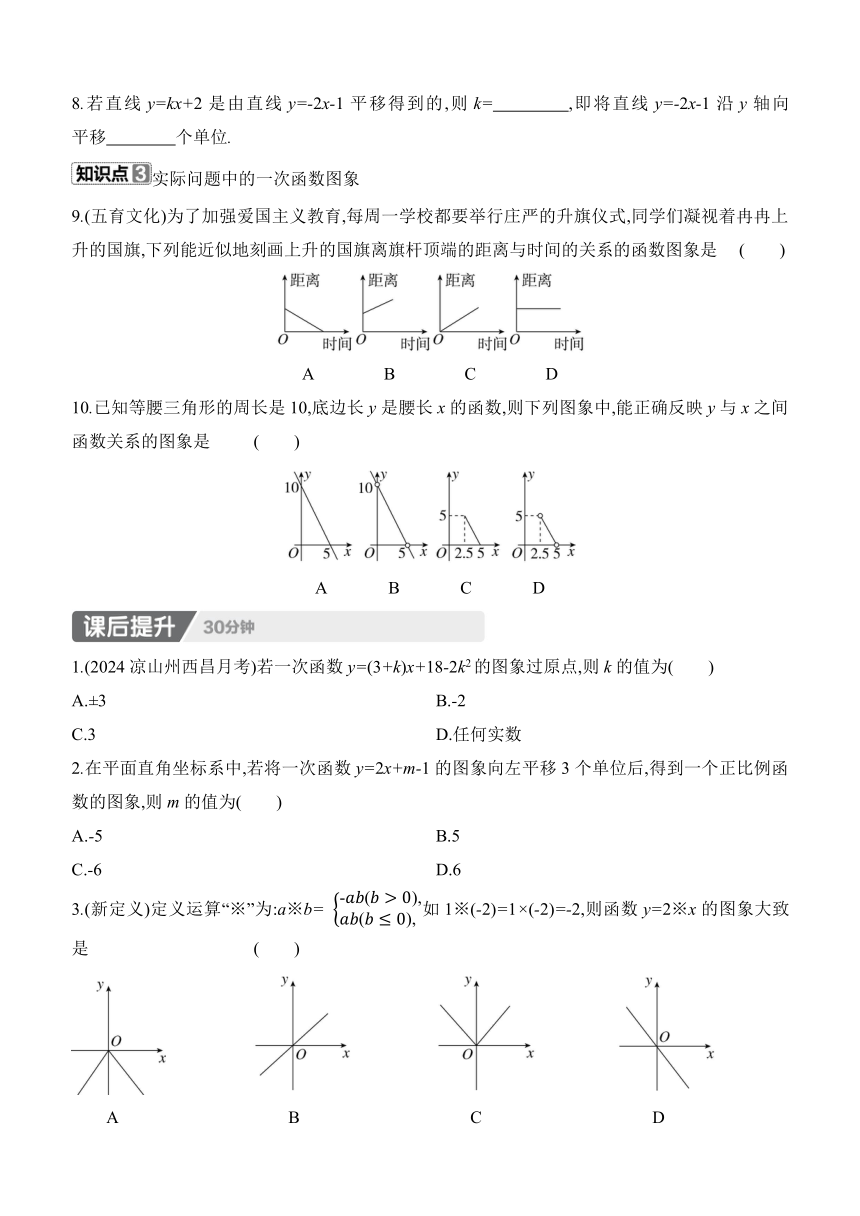
8.若直线y=kx+2是由直线y=-2x-1平移得到的,则k= ,即将直线y=-2x-1沿y轴向 平移 个单位.
实际问题中的一次函数图象
9.(五育文化)为了加强爱国主义教育,每周一学校都要举行庄严的升旗仪式,同学们凝视着冉冉上升的国旗,下列能近似地刻画上升的国旗离旗杆顶端的距离与时间的关系的函数图象是 ( )
A B C D
10.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是 ( )
A B C D
1.(2024凉山州西昌月考)若一次函数y=(3+k)x+18-2k2的图象过原点,则k的值为( )
A.±3 B.-2
C.3 D.任何实数
2.在平面直角坐标系中,若将一次函数y=2x+m-1的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )
A.-5 B.5
C.-6 D.6
3.(新定义)定义运算“※”为:a※b= 如1※(-2)=1×(-2)=-2,则函数y=2※x的图象大致是 ( )
A B C D
4.一次函数y1=k1x+b1的图象l1如图所示,将直线l1向下平移若干个单位后得直线l2,l2的函数关系式为y2=k2x+b2.则下列说法中错误的是 ( )
A.k1=k2 B.b1C.b1>b2 D.当x=5时,y1>y2
5.若点P(a,b)在一次函数y=2x-3的图象上,则代数式3b-6a+3的值为 .
6.(2024陇南武都城关中学月考)如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),已知直线l:y=x-2.
(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值.
(2)在(1)的条件下,平移后的直线与正方形的边BC交于点E,求△ABE的面积.
7.(推理能力)如图,已知正比例函数y=kx的图象经过点A,且点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,△AOH的面积为3.
(1)求正比例函数的关系式.
(2)在x轴上是否存在一点P,使△AOP的面积为5 若存在,求点P的坐标;若不存在,请说明理由.
【详解答案】
课堂达标
1.D 2.A 3.1 6 0
4.-1(答案不唯一,满足b<0即可)
5.解:(1)当y=0时,x=-1,
∴一次函数y=-2x-2的图象与x轴的交点A的坐标为(-1,0);
当x=0时,y=-2,
∴一次函数y=-2x-2的图象与y轴的交点B的坐标为(0,-2).
(2)列表如下:
x -1 0
y 0 -2
描点、连线,函数的图象如图所示.
6.A 7.A 8.-2 上 3 9.A 10.D
课后提升
1.C 解析:∵一次函数y=(3+k)x+18-2k2的图象过原点,∴18-2k2=0,解得k=±3.∵3+k≠0,∴k≠-3,∴k=3.故选C.
2.A 解析:将一次函数y=2x+m-1的图象向左平移3个单位后,得到y=2(x+3)+m-1的图象,把(0,0)代入y=2(x+3)+m-1,得0=6+m-1,解得m=-5.故选A.
3.A 解析:由题意得y=2※x=当x>0时,图象是正比例函数y=-2x的图象在第四象限的部分;当x≤0时,图象是正比例函数y=2x的图象在第三象限的部分及原点.故选A.
4.B 解析:∵将直线l1向下平移若干个单位后得直线l2,∴直线l1∥直线l2,b1>b2,∴k1=k2.∴当x=5时,y1>y2.故选B.
5.-6 解析:∵点P(a,b)在一次函数y=2x-3的图象上,∴b=2a-3,∴b-2a=-3,∴3b-6a+3=3(b-2a)+3=3×(-3)+3=-6.
6.解:(1)设平移后的直线方程为y=x+b,把点A的坐标(5,3)代入,得3=×5+b,解得b=,则平移后的直线方程为y=x+,则-2+m=,解得m=.
(2)如图,因为正方形ABCD的边长为2,且点A的坐标为(5,3),所以B(3,3).把x=3代入y=x+,得y=×3+=2,即E(3,2),所以BE=3-2=1,所以△ABE的面积为×2×1=1.
7.解:(1)∵点A的横坐标为3,AH⊥x轴,∴OH=3,
∵△AOH的面积为3,∴·OH·AH=×3×AH=3,∴AH=2.又∵点A在第四象限,
∴点A的坐标为(3,-2).
∵正比例函数y=kx的图象经过点A,
∴3k=-2,解得k=-.
∴正比例函数的关系式为y=-x.
(2)存在.
设点P的坐标为(a,0).
∵△AOP的面积为5,点A的坐标为(3,-2),
∴S△AOP=×|-2|×|a|=5,
∴|a|=5,
∴a=±5,∴点P的坐标为(5,0)或(-5,0).
一次函数的图象
1.下列各点在函数y=2x-1图象上的是 ( )
A.(-1,3) B.(0,1) C.(1,-1) D.(2,3)
2.一次函数y=-3x+1的图象经过 ( )
A.第一、二、四象限
B.第一、三、四象限
C.第一、二、三象限
D.第二、三、四象限
3.如果一次函数y=kx+4的图象经过点P(-1,3),则k= ;当x=2时,y= ;当y=4时, x= .
4.若一次函数y=-2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是 .(写出一个即可)
5.已知一次函数y=-2x-2.
(1)若该函数的图象与x轴、y轴分别交于A、B两点,求点A、B的坐标.
(2)在给定的平面直角坐标系(如图)中画出函数的图象.
一次函数图象的平移
6.将直线y=5x向下平移2个单位,所得直线的关系式为 ( )
A.y=5x-2 B.y=5x+2 C.y=5(x+2) D.y=5(x-2)
7.已知一次函数 y=kx+1的图象与y=x的图象平行,那么它必过点 ( )
A.(-1,0) B.(2,-1)
C.(2,1) D.(0,-1)
8.若直线y=kx+2是由直线y=-2x-1平移得到的,则k= ,即将直线y=-2x-1沿y轴向 平移 个单位.
实际问题中的一次函数图象
9.(五育文化)为了加强爱国主义教育,每周一学校都要举行庄严的升旗仪式,同学们凝视着冉冉上升的国旗,下列能近似地刻画上升的国旗离旗杆顶端的距离与时间的关系的函数图象是 ( )
A B C D
10.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是 ( )
A B C D
1.(2024凉山州西昌月考)若一次函数y=(3+k)x+18-2k2的图象过原点,则k的值为( )
A.±3 B.-2
C.3 D.任何实数
2.在平面直角坐标系中,若将一次函数y=2x+m-1的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )
A.-5 B.5
C.-6 D.6
3.(新定义)定义运算“※”为:a※b= 如1※(-2)=1×(-2)=-2,则函数y=2※x的图象大致是 ( )
A B C D
4.一次函数y1=k1x+b1的图象l1如图所示,将直线l1向下平移若干个单位后得直线l2,l2的函数关系式为y2=k2x+b2.则下列说法中错误的是 ( )
A.k1=k2 B.b1
5.若点P(a,b)在一次函数y=2x-3的图象上,则代数式3b-6a+3的值为 .
6.(2024陇南武都城关中学月考)如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),已知直线l:y=x-2.
(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值.
(2)在(1)的条件下,平移后的直线与正方形的边BC交于点E,求△ABE的面积.
7.(推理能力)如图,已知正比例函数y=kx的图象经过点A,且点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,△AOH的面积为3.
(1)求正比例函数的关系式.
(2)在x轴上是否存在一点P,使△AOP的面积为5 若存在,求点P的坐标;若不存在,请说明理由.
【详解答案】
课堂达标
1.D 2.A 3.1 6 0
4.-1(答案不唯一,满足b<0即可)
5.解:(1)当y=0时,x=-1,
∴一次函数y=-2x-2的图象与x轴的交点A的坐标为(-1,0);
当x=0时,y=-2,
∴一次函数y=-2x-2的图象与y轴的交点B的坐标为(0,-2).
(2)列表如下:
x -1 0
y 0 -2
描点、连线,函数的图象如图所示.
6.A 7.A 8.-2 上 3 9.A 10.D
课后提升
1.C 解析:∵一次函数y=(3+k)x+18-2k2的图象过原点,∴18-2k2=0,解得k=±3.∵3+k≠0,∴k≠-3,∴k=3.故选C.
2.A 解析:将一次函数y=2x+m-1的图象向左平移3个单位后,得到y=2(x+3)+m-1的图象,把(0,0)代入y=2(x+3)+m-1,得0=6+m-1,解得m=-5.故选A.
3.A 解析:由题意得y=2※x=当x>0时,图象是正比例函数y=-2x的图象在第四象限的部分;当x≤0时,图象是正比例函数y=2x的图象在第三象限的部分及原点.故选A.
4.B 解析:∵将直线l1向下平移若干个单位后得直线l2,∴直线l1∥直线l2,b1>b2,∴k1=k2.∴当x=5时,y1>y2.故选B.
5.-6 解析:∵点P(a,b)在一次函数y=2x-3的图象上,∴b=2a-3,∴b-2a=-3,∴3b-6a+3=3(b-2a)+3=3×(-3)+3=-6.
6.解:(1)设平移后的直线方程为y=x+b,把点A的坐标(5,3)代入,得3=×5+b,解得b=,则平移后的直线方程为y=x+,则-2+m=,解得m=.
(2)如图,因为正方形ABCD的边长为2,且点A的坐标为(5,3),所以B(3,3).把x=3代入y=x+,得y=×3+=2,即E(3,2),所以BE=3-2=1,所以△ABE的面积为×2×1=1.
7.解:(1)∵点A的横坐标为3,AH⊥x轴,∴OH=3,
∵△AOH的面积为3,∴·OH·AH=×3×AH=3,∴AH=2.又∵点A在第四象限,
∴点A的坐标为(3,-2).
∵正比例函数y=kx的图象经过点A,
∴3k=-2,解得k=-.
∴正比例函数的关系式为y=-x.
(2)存在.
设点P的坐标为(a,0).
∵△AOP的面积为5,点A的坐标为(3,-2),
∴S△AOP=×|-2|×|a|=5,
∴|a|=5,
∴a=±5,∴点P的坐标为(5,0)或(-5,0).
