19.1 矩形 1.矩形的性质 同步练(含答案)2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 19.1 矩形 1.矩形的性质 同步练(含答案)2024-2025学年数学华东师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 218.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:56:26 | ||
图片预览

文档简介
19.1 矩形
1.矩形的性质
矩形的定义以及对称性
1.(开放性试题)已知四边形 ABCD 是平行四边形,根据矩形的定义,添加一个条件: ,可使它成为矩形.
2.矩形有 条对称轴,通过对边 的直线是它的对称轴.
矩形的性质
3.如图,在矩形ABCD中,对角线AC、BD交于点O,若AC=14,则OB的长为 ( )
A.7 B.6 C.5 D.2
4.如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是 ( )
A.30° B.60° C.90° D.120
5.如图,在矩形ABCD中,对角线AC、BD相交于点O,已知∠BOC=120°,DC=3 cm,则AC的长为
cm.
矩形性质的应用
6.如图,过矩形ABCD的对角线BD上一点R分别作矩形两边的平行线MN与PQ,那么图中矩形AMRP的面积S1与矩形QCNR的面积S2的大小关系是 ( )
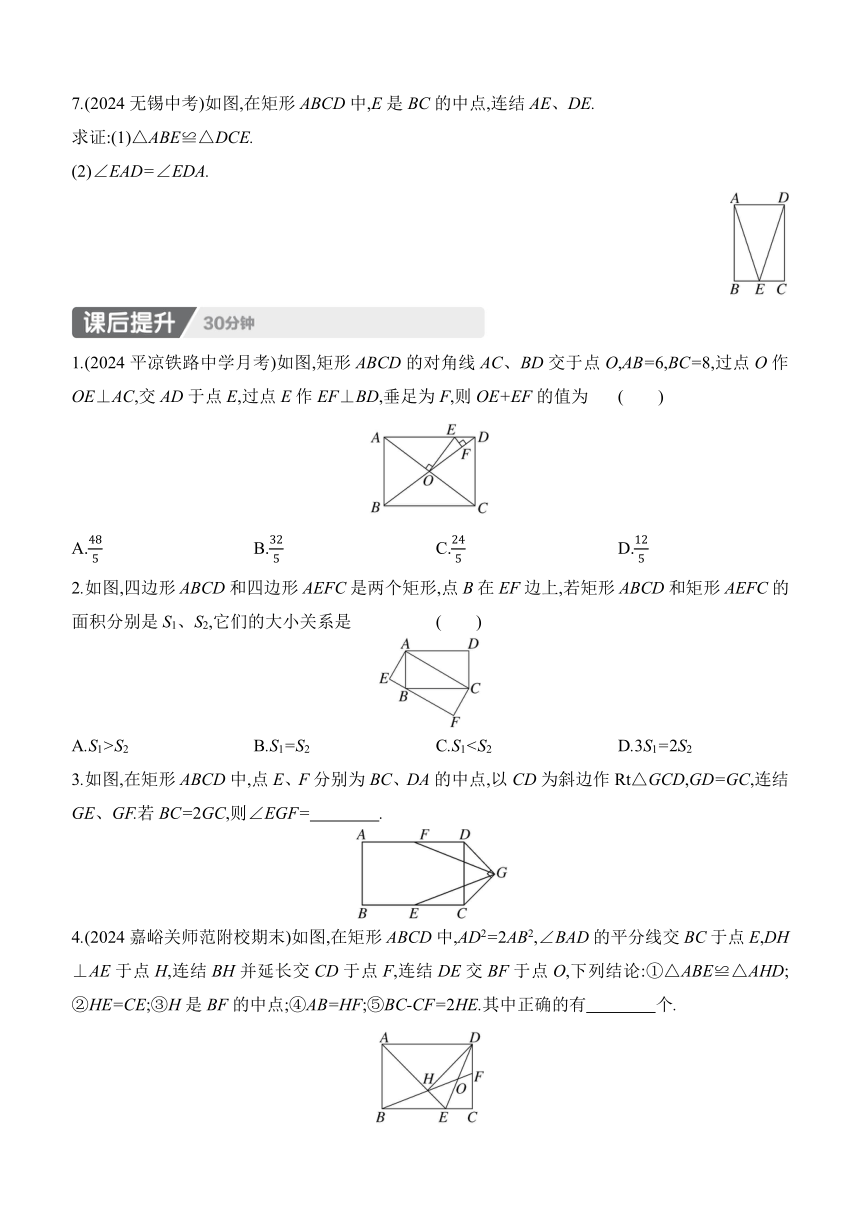
A.S1>S2 B.S1=S2 C.S17.(2024无锡中考)如图,在矩形ABCD中,E是BC的中点,连结AE、DE.
求证:(1)△ABE≌△DCE.
(2)∠EAD=∠EDA.
1.(2024平凉铁路中学月考)如图,矩形ABCD的对角线AC、BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为 ( )
A. B. C. D.
2.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2,它们的大小关系是 ( )
A.S1>S2 B.S1=S2 C.S13.如图,在矩形ABCD中,点E、F分别为BC、DA的中点,以CD为斜边作Rt△GCD,GD=GC,连结GE、GF.若BC=2GC,则∠EGF= .
4.(2024嘉峪关师范附校期末)如图,在矩形ABCD中,AD2=2AB2,∠BAD的平分线交BC于点E,DH⊥AE于点H,连结BH并延长交CD于点F,连结DE交BF于点O,下列结论:①△ABE≌△AHD;②HE=CE;③H是BF的中点;④AB=HF;⑤BC-CF=2HE.其中正确的有 个.
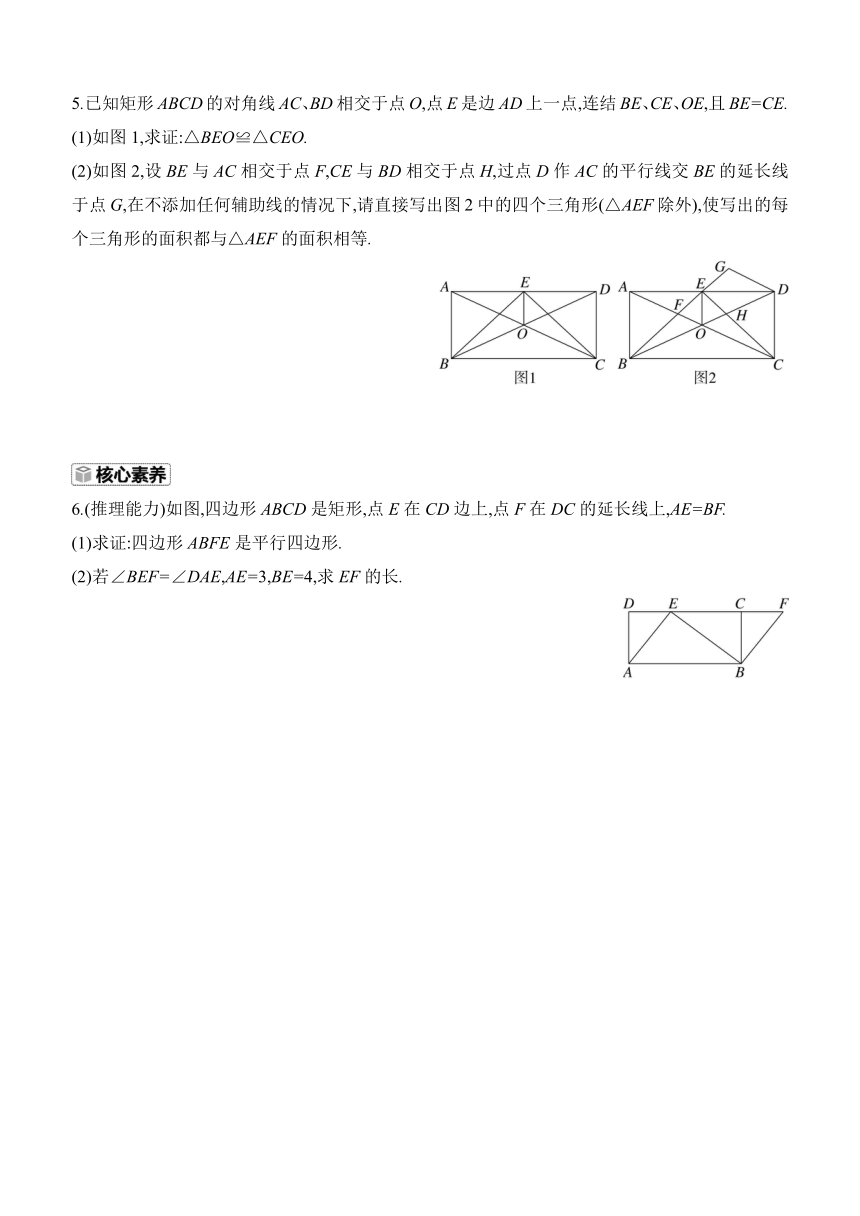
5.已知矩形ABCD的对角线AC、BD相交于点O,点E是边AD上一点,连结BE、CE、OE,且BE=CE.
(1)如图1,求证:△BEO≌△CEO.
(2)如图2,设BE与AC相交于点F,CE与BD相交于点H,过点D作AC的平行线交BE的延长线于点G,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(△AEF除外),使写出的每个三角形的面积都与△AEF的面积相等.
6.(推理能力)如图,四边形ABCD是矩形,点E在CD边上,点F在DC的延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形.
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
【详解答案】
课堂达标
1.∠A=90°(答案不唯一) 2.两 中点
3.A 4.C 5.6 6.B
7.证明:(1)∵四边形ABCD是矩形,
∴AB=DC,∠B=∠C=90°.
∵E是BC的中点,∴BE=CE,
在△ABE和△DCE中,
∴△ABE≌△DCE(S.A.S.).
(2)∵△ABE≌△DCE,
∴AE=DE,∴∠EAD=∠EDA.
课后提升
1.C 解析:∵AB=6,BC=8,∴矩形ABCD的面积为48,AC==10,∴AO=DO=AC=5.∵对角线AC、BD交于点O,∴△AOD的面积为12.∵OE⊥AO,EF⊥DO,∴S△AOD=S△AOE+S△DOE,即12=AO×OE+DO×EF,∴12=×5×OE+×5×EF,∴5(OE+EF)=24,∴OE+EF=.故选C.
2.B 解析:∵四边形ABCD是矩形,∴∠ABC=90°.∵矩形ABCD的面积S1=AB·BC,∴△ABC的面积为S△ABC=BC·AB.∴S1=2S△ABC.∵矩形AEFC的面积S2=AC·AE,△ABC的面积为S△ABC=AC·AE,∴S2=2S△ABC.∴S1=S2.故选B.
3.45° 解析:∵以CD为斜边作Rt△GCD,GD=GC,∴∠GDC=∠GCD=45°,∠DGC=90°,∴∠FDG=∠FDC+∠CDG=90°+45°=135°,∵点E、F分别为BC、DA的中点,BC=2GC,∴DF=DG,CE=CG,∴∠DGF=∠DFG=(180°-∠FDG)=×45°=22.5°,同理,可得∠CEG=∠CGE=(180°-∠ECG)=×45°=22.5°,∴∠EGF=∠DGC-∠DGF-∠EGC=90°-22.5°-22.5°=45°.
4.4 解析:∵在矩形ABCD中,∠BAD的平分线交BC于点E,DH⊥AE于点H,∴∠BAE=∠HAD=45°,∠ABE=∠AHD=90°,∴△ABE与△AHD是等腰直角三角形,∴AD2=2AH2,AE2=2AB2.∵AD2=2AB2,∴AH=AB,AD=AE.在△ABE与△AHD中,AH=AB,∠BAE=∠HAD=45°,AD=AE,∴△ABE≌△AHD(S.A.S.),故①正确.∵在矩形ABCD中,△ABE与△AHD是等腰直角三角形,△ABE≌△AHD,∴DH=AH=AB=BE,AD=AE=BC,∴AE-AH=BC-BE,∴HE=CE,故②正确.∵AB=AH,∴∠AHB=×(180°-45°)=67.5°,∴∠OHE=∠AHB=67.5°,∴∠DHO=90°-67.5°=22.5°.∵∠EBH=90°-67.5°=22.5°,∴∠EBH=∠DHO.在△BEH和△HDF中,∠DHO=∠EBH=22.5°,BE=DH,∠AEB=∠HDF=45°,∴△BEH≌△HDF(A.S.A.),∴BH=HF,即H是BF的中点,故③正确.∵AB=AH,∠BAE=45°,∴△ABH不是等边三角形,∴AB≠BH.∵BH=HF,∴AB≠HF,故④错误.∵CF=CD-DF,∴BC-CF=BC-(CD-DF).∵DF=HE,∴BC-CF=BC-(CD-HE)=BC-CD+HE.∵HE=AE-AH=BC-CD,∴BC-CF=HE+HE=2HE,故⑤正确.综上所述,正确的为①②③⑤,共有4个.
5.解:(1)∵四边形ABCD是矩形,∴OA=OC=AC,OB=OD=BD,AC=BD,∴OB=OC=OA=OD.∵BE=CE,OE=OE,∴△BEO≌△CEO(S.S.S.).
(2)△DHE,△CHO,△DEG,△BFO都与△AEF的面积相等.
解法提示:∵四边形ABCD是矩形,
∴∠BAD=∠CDA=90°,AB∥CD,AB=DC.
∵BE=CE,∴Rt△BAE≌Rt△CDE(H.L.),∴∠AEB=∠DEC,AE=DE.
∵OA=OD,∴∠OEA=∠OED=90°,∴∠BAD=∠OED=90°,∠ADC=∠AEO=90°,∴AB∥OE,DC∥OE,∴△AEO的面积=△BEO的面积,△DEO的面积=△COE的面积,∴△AEO的面积-△EFO的面积=△BEO的面积-△EFO的面积,△DEO的面积-△EHO的面积=△COE的面积-△EHO的面积,∴△AEF的面积=△BFO的面积,△DHE的面积=△CHO的面积.∵OA=OD,∴∠DAO=∠ADO,∴△AEF≌△DEH(A.S.A.),∴△AEF的面积=△DHE的面积=△CHO的面积=△BFO的面积.
∵DG∥AC,∴∠G=∠AFE,∠GDE=∠FAE,∴△AEF≌△DEG(A.A.S.),∴△AEF的面积=△DEG的面积,∴△DHE,△CHO,△DEG,△BFO都与△AEF的面积相等.
6.解:(1)证明:∵四边形ABCD是矩形,
∴AD=BC,∠D=∠BCD=90°,
∴∠BCF=180°-∠BCD=180°-90°=90°,
∴∠D=∠BCF.
在Rt△ADE和Rt△BCF中,
∴Rt△ADE≌Rt△BCF(H.L.),
∴∠AED=∠F.∴AE∥BF.
∵AE=BF,
∴四边形ABFE是平行四边形.
(2)∵∠D=90°,
∴∠DAE+∠AED=90°.
∵∠BEF=∠DAE,
∴∠BEF+∠AED=90°,∴∠AEB=90°.
在Rt△ABE中,AE=3,BE=4,由勾股定理,得AB===5.
∵四边形ABFE是平行四边形,
∴EF=AB=5.
1.矩形的性质
矩形的定义以及对称性
1.(开放性试题)已知四边形 ABCD 是平行四边形,根据矩形的定义,添加一个条件: ,可使它成为矩形.
2.矩形有 条对称轴,通过对边 的直线是它的对称轴.
矩形的性质
3.如图,在矩形ABCD中,对角线AC、BD交于点O,若AC=14,则OB的长为 ( )
A.7 B.6 C.5 D.2
4.如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是 ( )
A.30° B.60° C.90° D.120
5.如图,在矩形ABCD中,对角线AC、BD相交于点O,已知∠BOC=120°,DC=3 cm,则AC的长为
cm.
矩形性质的应用
6.如图,过矩形ABCD的对角线BD上一点R分别作矩形两边的平行线MN与PQ,那么图中矩形AMRP的面积S1与矩形QCNR的面积S2的大小关系是 ( )
A.S1>S2 B.S1=S2 C.S1
求证:(1)△ABE≌△DCE.
(2)∠EAD=∠EDA.
1.(2024平凉铁路中学月考)如图,矩形ABCD的对角线AC、BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为 ( )
A. B. C. D.
2.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2,它们的大小关系是 ( )
A.S1>S2 B.S1=S2 C.S1
4.(2024嘉峪关师范附校期末)如图,在矩形ABCD中,AD2=2AB2,∠BAD的平分线交BC于点E,DH⊥AE于点H,连结BH并延长交CD于点F,连结DE交BF于点O,下列结论:①△ABE≌△AHD;②HE=CE;③H是BF的中点;④AB=HF;⑤BC-CF=2HE.其中正确的有 个.
5.已知矩形ABCD的对角线AC、BD相交于点O,点E是边AD上一点,连结BE、CE、OE,且BE=CE.
(1)如图1,求证:△BEO≌△CEO.
(2)如图2,设BE与AC相交于点F,CE与BD相交于点H,过点D作AC的平行线交BE的延长线于点G,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(△AEF除外),使写出的每个三角形的面积都与△AEF的面积相等.
6.(推理能力)如图,四边形ABCD是矩形,点E在CD边上,点F在DC的延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形.
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
【详解答案】
课堂达标
1.∠A=90°(答案不唯一) 2.两 中点
3.A 4.C 5.6 6.B
7.证明:(1)∵四边形ABCD是矩形,
∴AB=DC,∠B=∠C=90°.
∵E是BC的中点,∴BE=CE,
在△ABE和△DCE中,
∴△ABE≌△DCE(S.A.S.).
(2)∵△ABE≌△DCE,
∴AE=DE,∴∠EAD=∠EDA.
课后提升
1.C 解析:∵AB=6,BC=8,∴矩形ABCD的面积为48,AC==10,∴AO=DO=AC=5.∵对角线AC、BD交于点O,∴△AOD的面积为12.∵OE⊥AO,EF⊥DO,∴S△AOD=S△AOE+S△DOE,即12=AO×OE+DO×EF,∴12=×5×OE+×5×EF,∴5(OE+EF)=24,∴OE+EF=.故选C.
2.B 解析:∵四边形ABCD是矩形,∴∠ABC=90°.∵矩形ABCD的面积S1=AB·BC,∴△ABC的面积为S△ABC=BC·AB.∴S1=2S△ABC.∵矩形AEFC的面积S2=AC·AE,△ABC的面积为S△ABC=AC·AE,∴S2=2S△ABC.∴S1=S2.故选B.
3.45° 解析:∵以CD为斜边作Rt△GCD,GD=GC,∴∠GDC=∠GCD=45°,∠DGC=90°,∴∠FDG=∠FDC+∠CDG=90°+45°=135°,∵点E、F分别为BC、DA的中点,BC=2GC,∴DF=DG,CE=CG,∴∠DGF=∠DFG=(180°-∠FDG)=×45°=22.5°,同理,可得∠CEG=∠CGE=(180°-∠ECG)=×45°=22.5°,∴∠EGF=∠DGC-∠DGF-∠EGC=90°-22.5°-22.5°=45°.
4.4 解析:∵在矩形ABCD中,∠BAD的平分线交BC于点E,DH⊥AE于点H,∴∠BAE=∠HAD=45°,∠ABE=∠AHD=90°,∴△ABE与△AHD是等腰直角三角形,∴AD2=2AH2,AE2=2AB2.∵AD2=2AB2,∴AH=AB,AD=AE.在△ABE与△AHD中,AH=AB,∠BAE=∠HAD=45°,AD=AE,∴△ABE≌△AHD(S.A.S.),故①正确.∵在矩形ABCD中,△ABE与△AHD是等腰直角三角形,△ABE≌△AHD,∴DH=AH=AB=BE,AD=AE=BC,∴AE-AH=BC-BE,∴HE=CE,故②正确.∵AB=AH,∴∠AHB=×(180°-45°)=67.5°,∴∠OHE=∠AHB=67.5°,∴∠DHO=90°-67.5°=22.5°.∵∠EBH=90°-67.5°=22.5°,∴∠EBH=∠DHO.在△BEH和△HDF中,∠DHO=∠EBH=22.5°,BE=DH,∠AEB=∠HDF=45°,∴△BEH≌△HDF(A.S.A.),∴BH=HF,即H是BF的中点,故③正确.∵AB=AH,∠BAE=45°,∴△ABH不是等边三角形,∴AB≠BH.∵BH=HF,∴AB≠HF,故④错误.∵CF=CD-DF,∴BC-CF=BC-(CD-DF).∵DF=HE,∴BC-CF=BC-(CD-HE)=BC-CD+HE.∵HE=AE-AH=BC-CD,∴BC-CF=HE+HE=2HE,故⑤正确.综上所述,正确的为①②③⑤,共有4个.
5.解:(1)∵四边形ABCD是矩形,∴OA=OC=AC,OB=OD=BD,AC=BD,∴OB=OC=OA=OD.∵BE=CE,OE=OE,∴△BEO≌△CEO(S.S.S.).
(2)△DHE,△CHO,△DEG,△BFO都与△AEF的面积相等.
解法提示:∵四边形ABCD是矩形,
∴∠BAD=∠CDA=90°,AB∥CD,AB=DC.
∵BE=CE,∴Rt△BAE≌Rt△CDE(H.L.),∴∠AEB=∠DEC,AE=DE.
∵OA=OD,∴∠OEA=∠OED=90°,∴∠BAD=∠OED=90°,∠ADC=∠AEO=90°,∴AB∥OE,DC∥OE,∴△AEO的面积=△BEO的面积,△DEO的面积=△COE的面积,∴△AEO的面积-△EFO的面积=△BEO的面积-△EFO的面积,△DEO的面积-△EHO的面积=△COE的面积-△EHO的面积,∴△AEF的面积=△BFO的面积,△DHE的面积=△CHO的面积.∵OA=OD,∴∠DAO=∠ADO,∴△AEF≌△DEH(A.S.A.),∴△AEF的面积=△DHE的面积=△CHO的面积=△BFO的面积.
∵DG∥AC,∴∠G=∠AFE,∠GDE=∠FAE,∴△AEF≌△DEG(A.A.S.),∴△AEF的面积=△DEG的面积,∴△DHE,△CHO,△DEG,△BFO都与△AEF的面积相等.
6.解:(1)证明:∵四边形ABCD是矩形,
∴AD=BC,∠D=∠BCD=90°,
∴∠BCF=180°-∠BCD=180°-90°=90°,
∴∠D=∠BCF.
在Rt△ADE和Rt△BCF中,
∴Rt△ADE≌Rt△BCF(H.L.),
∴∠AED=∠F.∴AE∥BF.
∵AE=BF,
∴四边形ABFE是平行四边形.
(2)∵∠D=90°,
∴∠DAE+∠AED=90°.
∵∠BEF=∠DAE,
∴∠BEF+∠AED=90°,∴∠AEB=90°.
在Rt△ABE中,AE=3,BE=4,由勾股定理,得AB===5.
∵四边形ABFE是平行四边形,
∴EF=AB=5.
