19.3 正方形 同步练(含答案)2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 19.3 正方形 同步练(含答案)2024-2025学年数学华东师大版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 191.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 13:58:43 | ||
图片预览


文档简介
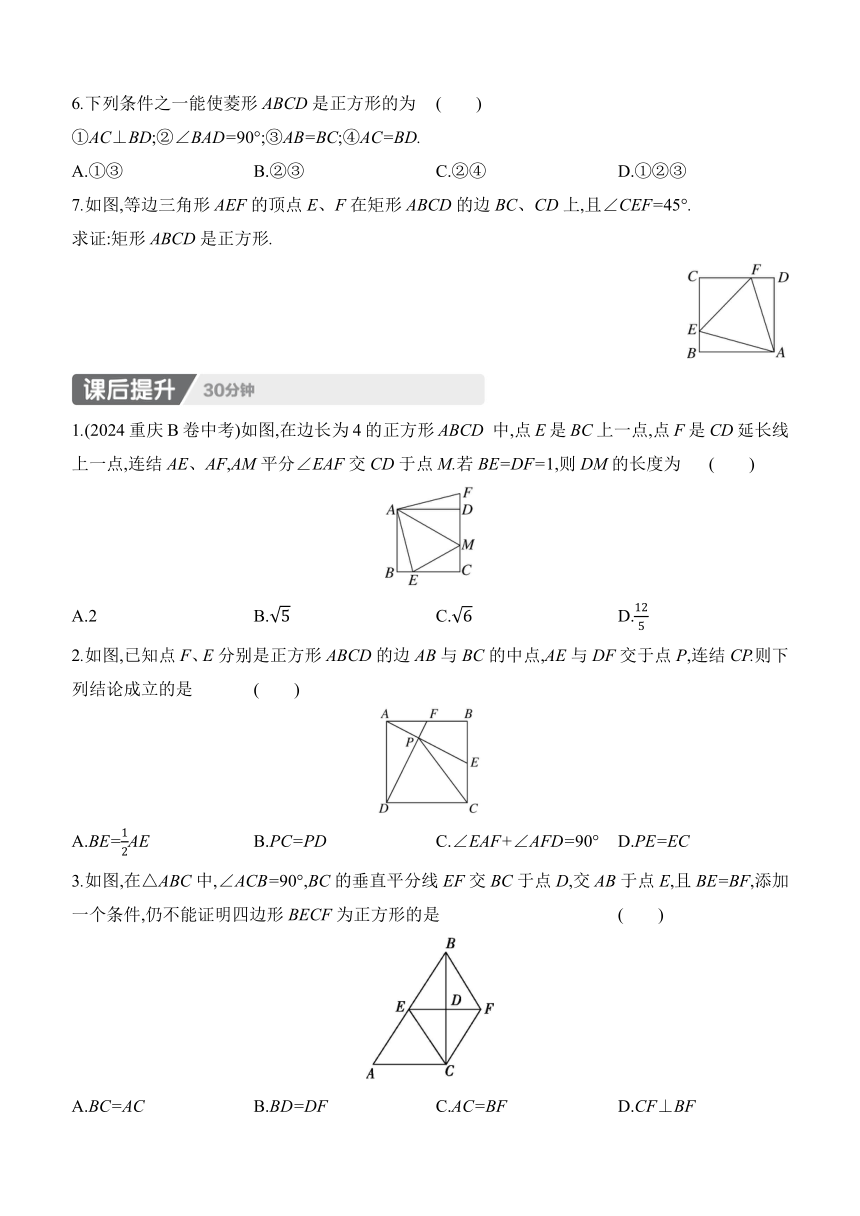
19.3 正方形
正方形的性质
1.正方形是轴对称图形,它的对称轴有 ( )
A.2条 B.4条 C.6条 D.8条
2.(2024宝鸡期末)如图,正方形ABCD的对角线AC、BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为 .
3.如图,在正方形ABCD的外侧作等边三角形ADE,连结BE,则∠BED的度数是 .
4.如图,在正方形ABCD中,AF=BE,AE与DF相交于点O.
(1)求证:△DAF≌△ABE.
(2)求∠AOD的度数.
正方形的判定
5.如图,在矩形ABCD中,对角线AC、BD相交于点O,添加下列一个条件,能使矩形ABCD成为正方形的是 ( )
A.BD=AB B.DC=AD
C.∠AOB=60° D.OD=CD
6.下列条件之一能使菱形ABCD是正方形的为 ( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③ B.②③ C.②④ D.①②③
7.如图,等边三角形AEF的顶点E、F在矩形ABCD的边BC、CD上,且∠CEF=45°.
求证:矩形ABCD是正方形.
1.(2024重庆B卷中考)如图,在边长为4的正方形ABCD 中,点E是BC上一点,点F是CD延长线上一点,连结AE、AF,AM平分∠EAF交CD于点M.若BE=DF=1,则DM的长度为 ( )
A.2 B. C. D.
2.如图,已知点F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,连结CP.则下列结论成立的是 ( )
A.BE=AE B.PC=PD C.∠EAF+∠AFD=90° D.PE=EC
3.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是 ( )
A.BC=AC B.BD=DF C.AC=BF D.CF⊥BF
4.(2024福建中考)如图,正方形ABCD的面积为4,点E、F、G、H分别为边AB、BC、CD、AD的中点,则四边形EFGH的面积为 .
5.已知:如图,在菱形ABCD中,点E、O、F分别为AB、AC、AD的中点,连结CE、CF、OE、OF,则OE=BC,OF=CD.
(1)求证:△BCE≌△DCF.
(2)当AB与BC满足什么关系时,四边形AEOF是正方形 请说明理由.
6.(推理能力)如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连结EF,EF与AD相交于点H.
(1)求证:AD⊥EF.
(2)△ABC 满足什么条件时,四边形AEDF 是正方形 说明理由.
【详解答案】
课堂达标
1.B 2.22.5° 3.45°
4.解:(1)证明:∵四边形ABCD是正方形,
∴∠DAB=∠ABC=90°,AD=AB.
在△DAF和△ABE中,
∴△DAF≌△ABE(S.A.S.).
(2)由(1)知△DAF≌△ABE,
∴∠ADF=∠BAE.∴∠ADF+∠DAO=∠BAE+∠DAO=∠DAB=90°.∴∠AOD=180°-(∠ADF+∠DAO)=90°.
5.B 6.C
7.证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,
∴易得∠CFE=∠CEF=45°,
∴∠AFD=∠AEB=180°-45°-60°=75°,
∴△AEB≌△AFD(A.A.S.),
∴AB=AD,
∴矩形ABCD是正方形.
课后提升
1.D 解析:∵四边形ABCD是正方形,∴AB=AD,∠ABE=∠ADF=90°,在△ABE和△ADF中,
∴△ABE≌△ADF(S.A.S.),∴AE=AF.
∵AM平分∠EAF,∴∠EAM=∠FAM,在△AEM和△AFM中,
∴△AEM≌△AFM(S.A.S.),∴EM=FM.∵四边形ABCD是正方形,∴BC=CD=4,∠BCD=90°,设DM=x,则MC=CD-DM=4-x,CE=BC-BE=4-1=3,EM=FM=FD+DM=1+x,在Rt△MCE中,根据勾股定理,得EM2=MC2+CE2,即(1+x)2=(4-x)2+32,解得x=.故选D.
2.C 解析:∵点F、E分别是正方形ABCD的边AB与BC的中点,∴AF=BE.在△AFD和△BEA中,
∴△AFD≌△BEA(S.A.S.).∴∠FDA=∠EAB.又∵∠FDA+∠AFD=90°,∴∠EAB+∠AFD=90°,即∠EAF+∠AFD=90°.故C正确.A、B、D无法证明其成立.故选C.
3.C 解析:∵EF垂直平分BC,∴BE=EC,BF=CF.∵BF=BE,∴BE=EC=CF=BF.∴四边形BECF是菱形.当BC=AC时,∵∠ACB=90°,∴∠A=∠EBC=45°.∴∠EBF=2∠EBC=2×45°=90°.∴菱形BECF是正方形.故选项A不符合题意;当BD=DF时,利用正方形的判定得出,菱形BECF是正方形,故选项B不符合题意;当AC=BF时,无法得出菱形BECF是正方形,故选项C符合题意;当CF⊥BF时,利用正方形的判定得出,菱形BECF是正方形,故选项D不符合题意.故选C.
4.2 解析:∵正方形ABCD的面积为4,∴AB=BC=CD=AD=2,∠D=90°.∵点E、F、G、H分别为边AB、BC、CD、AD的中点,∴HD=DG=1,∴S△DGH=×1×1=,同理可得S△AHE=S△EFB=S△CGF=,∴四边形EFGH的面积为4----=2.
5.解:(1)证明:∵四边形ABCD为菱形,
∴AB=BC=CD=DA,∠B=∠D.
又∵点E、F分别是AB、AD的中点,
∴BE=DF.∴△BCE≌△DCF(S.A.S.).
(2)当AB⊥BC时,四边形AEOF为正方形.
理由如下:
在菱形ABCD中,AD=BC,
∵OE=BC,AF=AD,∴OE=AF.同理,AE=OF.
∴四边形AEOF为平行四边形.
∵E、F分别是AB、AD的中点,∴AE=AF,
∴ AEOF为菱形.
∵BC⊥AB,∴∠B=90°.
∴∠BAD=90°.
∴菱形AEOF为正方形.
6.解:(1)证明:∵AD是△ABC的角平分线,
∴∠EAD=∠FAD.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
在△AED和△AFD中,
∴△AED≌△AFD(A.A.S.),
∴AE=AF,∴AD⊥EF.
(2)△ABC满足∠BAC=90°时,四边形AEDF是正方形,理由:
∵∠AED=∠AFD=∠BAC=90°,
∴四边形AEDF是矩形.
∵AE=AF,
∴矩形AEDF是正方形.
正方形的性质
1.正方形是轴对称图形,它的对称轴有 ( )
A.2条 B.4条 C.6条 D.8条
2.(2024宝鸡期末)如图,正方形ABCD的对角线AC、BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为 .
3.如图,在正方形ABCD的外侧作等边三角形ADE,连结BE,则∠BED的度数是 .
4.如图,在正方形ABCD中,AF=BE,AE与DF相交于点O.
(1)求证:△DAF≌△ABE.
(2)求∠AOD的度数.
正方形的判定
5.如图,在矩形ABCD中,对角线AC、BD相交于点O,添加下列一个条件,能使矩形ABCD成为正方形的是 ( )
A.BD=AB B.DC=AD
C.∠AOB=60° D.OD=CD
6.下列条件之一能使菱形ABCD是正方形的为 ( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③ B.②③ C.②④ D.①②③
7.如图,等边三角形AEF的顶点E、F在矩形ABCD的边BC、CD上,且∠CEF=45°.
求证:矩形ABCD是正方形.
1.(2024重庆B卷中考)如图,在边长为4的正方形ABCD 中,点E是BC上一点,点F是CD延长线上一点,连结AE、AF,AM平分∠EAF交CD于点M.若BE=DF=1,则DM的长度为 ( )
A.2 B. C. D.
2.如图,已知点F、E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,连结CP.则下列结论成立的是 ( )
A.BE=AE B.PC=PD C.∠EAF+∠AFD=90° D.PE=EC
3.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是 ( )
A.BC=AC B.BD=DF C.AC=BF D.CF⊥BF
4.(2024福建中考)如图,正方形ABCD的面积为4,点E、F、G、H分别为边AB、BC、CD、AD的中点,则四边形EFGH的面积为 .
5.已知:如图,在菱形ABCD中,点E、O、F分别为AB、AC、AD的中点,连结CE、CF、OE、OF,则OE=BC,OF=CD.
(1)求证:△BCE≌△DCF.
(2)当AB与BC满足什么关系时,四边形AEOF是正方形 请说明理由.
6.(推理能力)如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连结EF,EF与AD相交于点H.
(1)求证:AD⊥EF.
(2)△ABC 满足什么条件时,四边形AEDF 是正方形 说明理由.
【详解答案】
课堂达标
1.B 2.22.5° 3.45°
4.解:(1)证明:∵四边形ABCD是正方形,
∴∠DAB=∠ABC=90°,AD=AB.
在△DAF和△ABE中,
∴△DAF≌△ABE(S.A.S.).
(2)由(1)知△DAF≌△ABE,
∴∠ADF=∠BAE.∴∠ADF+∠DAO=∠BAE+∠DAO=∠DAB=90°.∴∠AOD=180°-(∠ADF+∠DAO)=90°.
5.B 6.C
7.证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,
∴易得∠CFE=∠CEF=45°,
∴∠AFD=∠AEB=180°-45°-60°=75°,
∴△AEB≌△AFD(A.A.S.),
∴AB=AD,
∴矩形ABCD是正方形.
课后提升
1.D 解析:∵四边形ABCD是正方形,∴AB=AD,∠ABE=∠ADF=90°,在△ABE和△ADF中,
∴△ABE≌△ADF(S.A.S.),∴AE=AF.
∵AM平分∠EAF,∴∠EAM=∠FAM,在△AEM和△AFM中,
∴△AEM≌△AFM(S.A.S.),∴EM=FM.∵四边形ABCD是正方形,∴BC=CD=4,∠BCD=90°,设DM=x,则MC=CD-DM=4-x,CE=BC-BE=4-1=3,EM=FM=FD+DM=1+x,在Rt△MCE中,根据勾股定理,得EM2=MC2+CE2,即(1+x)2=(4-x)2+32,解得x=.故选D.
2.C 解析:∵点F、E分别是正方形ABCD的边AB与BC的中点,∴AF=BE.在△AFD和△BEA中,
∴△AFD≌△BEA(S.A.S.).∴∠FDA=∠EAB.又∵∠FDA+∠AFD=90°,∴∠EAB+∠AFD=90°,即∠EAF+∠AFD=90°.故C正确.A、B、D无法证明其成立.故选C.
3.C 解析:∵EF垂直平分BC,∴BE=EC,BF=CF.∵BF=BE,∴BE=EC=CF=BF.∴四边形BECF是菱形.当BC=AC时,∵∠ACB=90°,∴∠A=∠EBC=45°.∴∠EBF=2∠EBC=2×45°=90°.∴菱形BECF是正方形.故选项A不符合题意;当BD=DF时,利用正方形的判定得出,菱形BECF是正方形,故选项B不符合题意;当AC=BF时,无法得出菱形BECF是正方形,故选项C符合题意;当CF⊥BF时,利用正方形的判定得出,菱形BECF是正方形,故选项D不符合题意.故选C.
4.2 解析:∵正方形ABCD的面积为4,∴AB=BC=CD=AD=2,∠D=90°.∵点E、F、G、H分别为边AB、BC、CD、AD的中点,∴HD=DG=1,∴S△DGH=×1×1=,同理可得S△AHE=S△EFB=S△CGF=,∴四边形EFGH的面积为4----=2.
5.解:(1)证明:∵四边形ABCD为菱形,
∴AB=BC=CD=DA,∠B=∠D.
又∵点E、F分别是AB、AD的中点,
∴BE=DF.∴△BCE≌△DCF(S.A.S.).
(2)当AB⊥BC时,四边形AEOF为正方形.
理由如下:
在菱形ABCD中,AD=BC,
∵OE=BC,AF=AD,∴OE=AF.同理,AE=OF.
∴四边形AEOF为平行四边形.
∵E、F分别是AB、AD的中点,∴AE=AF,
∴ AEOF为菱形.
∵BC⊥AB,∴∠B=90°.
∴∠BAD=90°.
∴菱形AEOF为正方形.
6.解:(1)证明:∵AD是△ABC的角平分线,
∴∠EAD=∠FAD.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
在△AED和△AFD中,
∴△AED≌△AFD(A.A.S.),
∴AE=AF,∴AD⊥EF.
(2)△ABC满足∠BAC=90°时,四边形AEDF是正方形,理由:
∵∠AED=∠AFD=∠BAC=90°,
∴四边形AEDF是矩形.
∵AE=AF,
∴矩形AEDF是正方形.
