20.2 数据的集中趋势 2.平均数、中位数和众数的选用 同步练(含答案)2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 20.2 数据的集中趋势 2.平均数、中位数和众数的选用 同步练(含答案)2024-2025学年数学华东师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 139.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 00:00:00 | ||
图片预览

文档简介
2.平均数、中位数和众数的选用
平均数、中位数、众数的选用
1.在暑假到来之前,某机构向八年级学生推荐了A、B、C三条游学线路,现对该年级学生喜欢哪一条游学线路做调查,以决定最终的游学线路,下面的统计量中最值得关注的是 ( )
A.众数 B.平均数
C.中位数 D.无法确定
2.某校举办水浒文化进校园朗诵大赛,比赛中七位评委给某位参赛选手的分数,如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是 ( )
A.中位数 B.众数
C.平均数 D.中位数和众数
3.某商店试销一款女式上衣,试销期间对不同颜色女式上衣的销售情况做了统计,商店经理最关心的是哪种颜色的女式上衣最畅销,则对商店经理最有意义的统计量是 .(填“平均数”“中位数”或“众数”)
4.某公司为提高服务质量,对其某个部门开展了客户满意度问卷调查,客户满意度以分数呈现,满意度从低到高为1分、2分、3分、4分、5分,共5档.公司规定:若客户所评分数的平均数或中位数低于3.5分,则该部门需要对服务质量进行整改.工作人员从收回的问卷中抽取了20份,下图是根据这20份问卷中的客户所评分数绘制的统计图.
(1)求客户所评分数的中位数、平均数,并判断该部门是否需要整改.
(2)监督人员从余下的问卷中又抽取了1份,与之前的20份合在一起,重新计算后,发现客户所评分数的平均数大于3.55分,求监督人员抽取的问卷所评分数为几分,与(1)相比,中位数是否发生变化
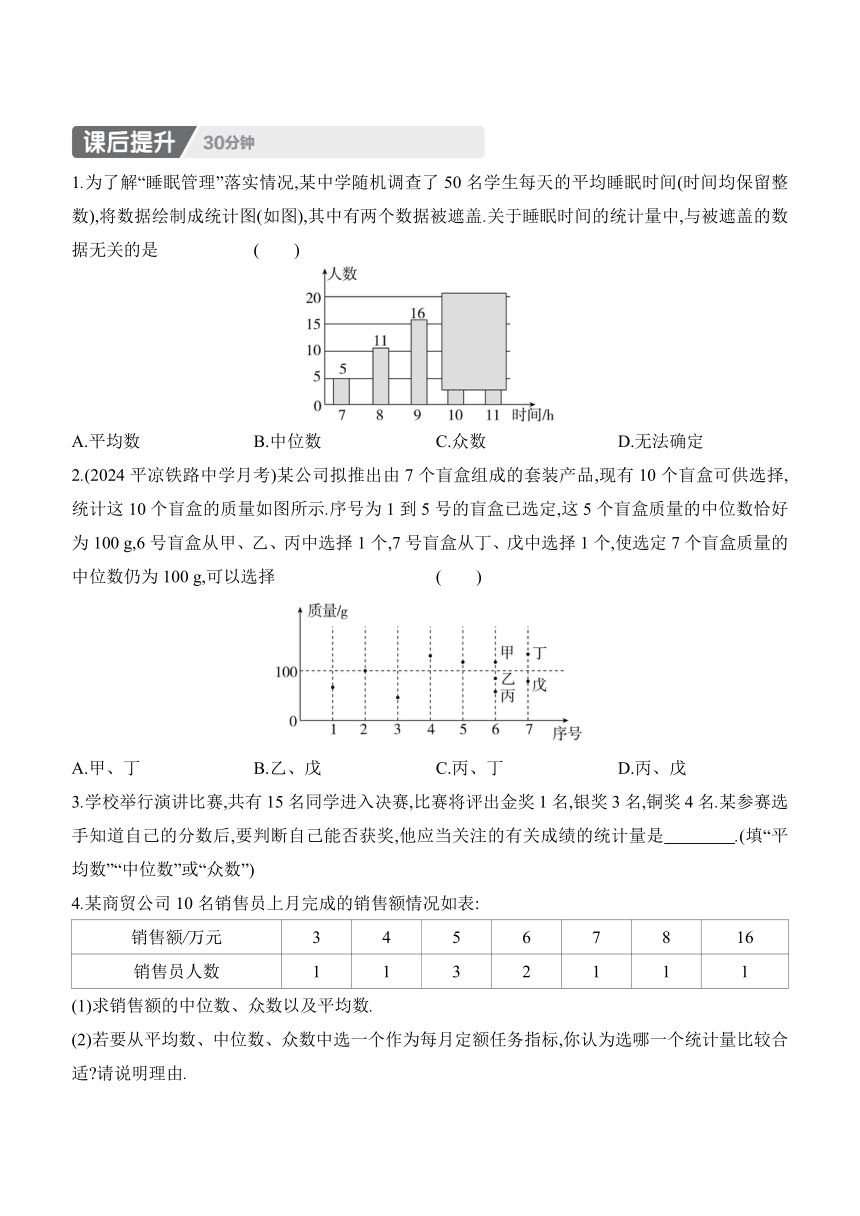
1.为了解“睡眠管理”落实情况,某中学随机调查了50名学生每天的平均睡眠时间(时间均保留整数),将数据绘制成统计图(如图),其中有两个数据被遮盖.关于睡眠时间的统计量中,与被遮盖的数据无关的是 ( )
A.平均数 B.中位数 C.众数 D.无法确定
2.(2024平凉铁路中学月考)某公司拟推出由7个盲盒组成的套装产品,现有10个盲盒可供选择,统计这10个盲盒的质量如图所示.序号为1到5号的盲盒已选定,这5个盲盒质量的中位数恰好为100 g,6号盲盒从甲、乙、丙中选择1个,7号盲盒从丁、戊中选择1个,使选定7个盲盒质量的中位数仍为100 g,可以选择 ( )
A.甲、丁 B.乙、戊 C.丙、丁 D.丙、戊
3.学校举行演讲比赛,共有15名同学进入决赛,比赛将评出金奖1名,银奖3名,铜奖4名.某参赛选手知道自己的分数后,要判断自己能否获奖,他应当关注的有关成绩的统计量是 .(填“平均数”“中位数”或“众数”)
4.某商贸公司10名销售员上月完成的销售额情况如表:
销售额/万元 3 4 5 6 7 8 16
销售员人数 1 1 3 2 1 1 1
(1)求销售额的中位数、众数以及平均数.
(2)若要从平均数、中位数、众数中选一个作为每月定额任务指标,你认为选哪一个统计量比较合适 请说明理由.
5.(应用意识)为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,初中三个年级根据初赛成绩分别选出了6名同学参加决赛,这些选手的决赛成绩如下表所示:
年级 决赛成绩
七年级 86 90 88 90 90 96
八年级 85 86 92 92 87 98
九年级 88 84 93 99 88 88
(1)下表是根据三个年级同学的决赛成绩得到的统计表:
年级 平均数 中位数 众数
七年级 90 90 a
八年级 90 b 92
九年级 90 88 88
请你补充上表中a,b的值,a= ,b= .
(2)请从以下两个不同角度对三个年级的决赛进行分析:
①从平均数和中位数相结合看,哪个年级成绩更好些;
②从平均数和众数相结合看,哪个年级成绩更好些.
(3)在每个年级参加决赛的选手中分别选出2名同学参加总决赛,你认为哪个年级的实力更强些,并说明理由.
【详解答案】
课堂达标
1.A 2.A 3.众数
4.解:(1)由条形统计图可知,客户所评分数按从小到大排列后,第10个数据是3分,第11个数据是4分,
∴客户所评分数的中位数为=3.5(分).
由统计图可知,客户所评分数的平均数为=3.5(分),
∴客户所评分数的平均数和中位数都不低于3.5分.
∴该部门不需要整改.
(2)设监督人员抽取的问卷所评分数为x分,则有>3.55,解得x>4.55,
∵满意度从低到高为1分、2分、3分、4分、5分,共5档,
∴监督人员抽取的问卷所评分数为5分.
∵4<5,
∴加入这个数据,客户所评分数按从小到大排列之后,第11个数据是4分.
即加入这个数据之后,中位数是4分.
∴与(1)相比,中位数发生了变化,由3.5分变成4分.
课后提升
1.B 解析:由统计图可知,平均数无法计算,众数无法确定,而中位数是(9+9)÷2=9.故选B.
2.C 解析:∵要推出由7个盲盒组成的套装产品,∴中位数应该是质量由小到大排列的第4个盲盒,∵序号为1到5号的盲盒已选定,这5个盲盒质量的中位数恰好为100 g,6号盲盒从甲、乙、丙中选择1个,7号盲盒从丁、戊中选择1个,使选定7个盲盒质量的中位数仍为100 g,∴选定的6号盲盒和7号盲盒的质量应该一个超过100 g,另一个低于100 g,∴可以选择甲,戊或乙,丁或丙,丁.∵选项中只有丙,丁,故选C.
3.中位数 解析:共有1+3+4=8(个)获奖名额,所以这15名学生所得分数的中位数即是获奖的学生中的最低分,所以某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数.
4.解:(1)∵共有10人,∴中位数应该是排序后第5个和第6个销售额的平均数,∴中位数为=5.5(万元).
∵销售额为5万元的有3人,人数最多,∴销售额的众数为5万元.
平均数为×(3+4+5×3+6×2+7+8+16)=6.5(万元).
(2)众数.理由:如果以销售额的中位数作为每月定额任务指标,那么没有完成定额任务的销售员有5人.如果以销售额的众数作为每月定额任务指标,那么没有完成定额任务的销售员有2人.如果以销售额的平均数作为每月定额任务指标,那么没有完成定额任务的销售员有7人,所以选择众数比较合适.
5.解:(1)90 89.5
(2)①从平均数和中位数相结合看,三个年级成绩的平均数相等,而七年级成绩的中位数最大,
所以七年级得90分及以上的人数最多,
所以七年级成绩更好些.
②从平均数和众数相结合看,三个年级的平均数相等,而八年级成绩的众数最大,
所以八年级得92分的人数最多,
所以八年级成绩更好些.
(3)九年级的实力更强些.理由如下:
因为九年级前两名同学的决赛成绩的平均分大于其他年级的,所以九年级的实力更强些.(答案不唯一,合理即可)
平均数、中位数、众数的选用
1.在暑假到来之前,某机构向八年级学生推荐了A、B、C三条游学线路,现对该年级学生喜欢哪一条游学线路做调查,以决定最终的游学线路,下面的统计量中最值得关注的是 ( )
A.众数 B.平均数
C.中位数 D.无法确定
2.某校举办水浒文化进校园朗诵大赛,比赛中七位评委给某位参赛选手的分数,如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是 ( )
A.中位数 B.众数
C.平均数 D.中位数和众数
3.某商店试销一款女式上衣,试销期间对不同颜色女式上衣的销售情况做了统计,商店经理最关心的是哪种颜色的女式上衣最畅销,则对商店经理最有意义的统计量是 .(填“平均数”“中位数”或“众数”)
4.某公司为提高服务质量,对其某个部门开展了客户满意度问卷调查,客户满意度以分数呈现,满意度从低到高为1分、2分、3分、4分、5分,共5档.公司规定:若客户所评分数的平均数或中位数低于3.5分,则该部门需要对服务质量进行整改.工作人员从收回的问卷中抽取了20份,下图是根据这20份问卷中的客户所评分数绘制的统计图.
(1)求客户所评分数的中位数、平均数,并判断该部门是否需要整改.
(2)监督人员从余下的问卷中又抽取了1份,与之前的20份合在一起,重新计算后,发现客户所评分数的平均数大于3.55分,求监督人员抽取的问卷所评分数为几分,与(1)相比,中位数是否发生变化
1.为了解“睡眠管理”落实情况,某中学随机调查了50名学生每天的平均睡眠时间(时间均保留整数),将数据绘制成统计图(如图),其中有两个数据被遮盖.关于睡眠时间的统计量中,与被遮盖的数据无关的是 ( )
A.平均数 B.中位数 C.众数 D.无法确定
2.(2024平凉铁路中学月考)某公司拟推出由7个盲盒组成的套装产品,现有10个盲盒可供选择,统计这10个盲盒的质量如图所示.序号为1到5号的盲盒已选定,这5个盲盒质量的中位数恰好为100 g,6号盲盒从甲、乙、丙中选择1个,7号盲盒从丁、戊中选择1个,使选定7个盲盒质量的中位数仍为100 g,可以选择 ( )
A.甲、丁 B.乙、戊 C.丙、丁 D.丙、戊
3.学校举行演讲比赛,共有15名同学进入决赛,比赛将评出金奖1名,银奖3名,铜奖4名.某参赛选手知道自己的分数后,要判断自己能否获奖,他应当关注的有关成绩的统计量是 .(填“平均数”“中位数”或“众数”)
4.某商贸公司10名销售员上月完成的销售额情况如表:
销售额/万元 3 4 5 6 7 8 16
销售员人数 1 1 3 2 1 1 1
(1)求销售额的中位数、众数以及平均数.
(2)若要从平均数、中位数、众数中选一个作为每月定额任务指标,你认为选哪一个统计量比较合适 请说明理由.
5.(应用意识)为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,初中三个年级根据初赛成绩分别选出了6名同学参加决赛,这些选手的决赛成绩如下表所示:
年级 决赛成绩
七年级 86 90 88 90 90 96
八年级 85 86 92 92 87 98
九年级 88 84 93 99 88 88
(1)下表是根据三个年级同学的决赛成绩得到的统计表:
年级 平均数 中位数 众数
七年级 90 90 a
八年级 90 b 92
九年级 90 88 88
请你补充上表中a,b的值,a= ,b= .
(2)请从以下两个不同角度对三个年级的决赛进行分析:
①从平均数和中位数相结合看,哪个年级成绩更好些;
②从平均数和众数相结合看,哪个年级成绩更好些.
(3)在每个年级参加决赛的选手中分别选出2名同学参加总决赛,你认为哪个年级的实力更强些,并说明理由.
【详解答案】
课堂达标
1.A 2.A 3.众数
4.解:(1)由条形统计图可知,客户所评分数按从小到大排列后,第10个数据是3分,第11个数据是4分,
∴客户所评分数的中位数为=3.5(分).
由统计图可知,客户所评分数的平均数为=3.5(分),
∴客户所评分数的平均数和中位数都不低于3.5分.
∴该部门不需要整改.
(2)设监督人员抽取的问卷所评分数为x分,则有>3.55,解得x>4.55,
∵满意度从低到高为1分、2分、3分、4分、5分,共5档,
∴监督人员抽取的问卷所评分数为5分.
∵4<5,
∴加入这个数据,客户所评分数按从小到大排列之后,第11个数据是4分.
即加入这个数据之后,中位数是4分.
∴与(1)相比,中位数发生了变化,由3.5分变成4分.
课后提升
1.B 解析:由统计图可知,平均数无法计算,众数无法确定,而中位数是(9+9)÷2=9.故选B.
2.C 解析:∵要推出由7个盲盒组成的套装产品,∴中位数应该是质量由小到大排列的第4个盲盒,∵序号为1到5号的盲盒已选定,这5个盲盒质量的中位数恰好为100 g,6号盲盒从甲、乙、丙中选择1个,7号盲盒从丁、戊中选择1个,使选定7个盲盒质量的中位数仍为100 g,∴选定的6号盲盒和7号盲盒的质量应该一个超过100 g,另一个低于100 g,∴可以选择甲,戊或乙,丁或丙,丁.∵选项中只有丙,丁,故选C.
3.中位数 解析:共有1+3+4=8(个)获奖名额,所以这15名学生所得分数的中位数即是获奖的学生中的最低分,所以某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数.
4.解:(1)∵共有10人,∴中位数应该是排序后第5个和第6个销售额的平均数,∴中位数为=5.5(万元).
∵销售额为5万元的有3人,人数最多,∴销售额的众数为5万元.
平均数为×(3+4+5×3+6×2+7+8+16)=6.5(万元).
(2)众数.理由:如果以销售额的中位数作为每月定额任务指标,那么没有完成定额任务的销售员有5人.如果以销售额的众数作为每月定额任务指标,那么没有完成定额任务的销售员有2人.如果以销售额的平均数作为每月定额任务指标,那么没有完成定额任务的销售员有7人,所以选择众数比较合适.
5.解:(1)90 89.5
(2)①从平均数和中位数相结合看,三个年级成绩的平均数相等,而七年级成绩的中位数最大,
所以七年级得90分及以上的人数最多,
所以七年级成绩更好些.
②从平均数和众数相结合看,三个年级的平均数相等,而八年级成绩的众数最大,
所以八年级得92分的人数最多,
所以八年级成绩更好些.
(3)九年级的实力更强些.理由如下:
因为九年级前两名同学的决赛成绩的平均分大于其他年级的,所以九年级的实力更强些.(答案不唯一,合理即可)
